The sectional curvature of the infinite dimensional manifold of Hölder equilibrium probabilities

Abstract

Here we consider the discrete time dynamics described by a transformation 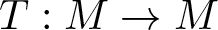$T:M \to M$, where T is either the action of shift 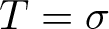$T=\sigma$ on the symbolic space 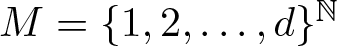$M=\{1,2, \ldots,d\}^{\mathbb{N}}$, or, T describes the action of a d to 1 expanding transformation 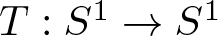$T:S^1 \to S^1$ of class 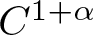$C^{1+\alpha}$ (for example 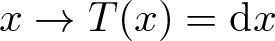$x \to T(x) =\mathrm{d} x $ (mod 1)), where 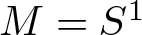$M=S^1$ is the unit circle. It is known that the infinite-dimensional manifold $\mathcal{N}$ of Hölder equilibrium probabilities is an analytical manifold and carries a natural Riemannian metric. Given a certain normalized Hölder potential A denote by 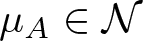$\mu_A \in \mathcal{N}$ the associated equilibrium probability. The set of tangent vectors X (functions 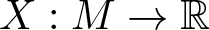$X: M \to \mathbb{R}$) to the manifold $\mathcal{N}$ at the point µ_A (a subspace of the Hilbert space 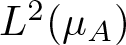$L^2(\mu_A)$) coincides with the kernel of the Ruelle operator for the normalized potential A. The Riemannian norm 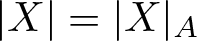$|X|=|X|_A$ of the vector X, which is tangent to $\mathcal{N}$ at the point µ_A, is described via the asymptotic variance, that is, satisfies

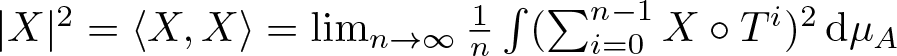$ |X|^2 = \langle X, X \rangle = \lim_{n \to \infty}\frac{1}{n} \int (\sum_{i=0}^{n-1} X\circ T^i )^2 \,\mathrm{d} \mu_A$.

Consider an orthonormal basis X_i, 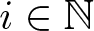$i \in \mathbb{N}$, for the tangent space at µ_A. For any two orthonormal vectors X and Y on the basis, the curvature 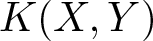$K(X,Y)$ is

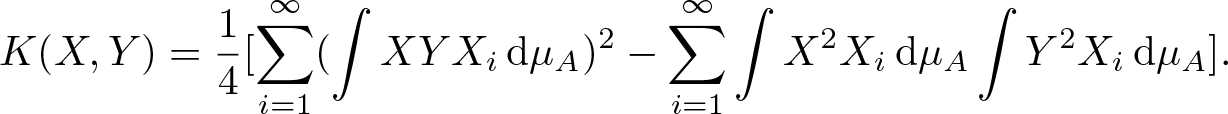\begin{equation*}K(X,Y) = \frac{1}{4}[ \sum_{i=1}^\infty (\int X Y X_i \,\mathrm{d} \mu_A)^2 - \sum_{i=1}^\infty \int X^2 X_i \,\mathrm{d} \mu_A \int Y^2 X_i \,\mathrm{d} \mu_A ].\end{equation*}

When the equilibrium probabilities µ_A is the set of invariant Markov probabilities on 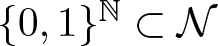$\{0,1\}^{\mathbb{N}}\subset \mathcal{N}$, introducing an orthonormal basis 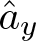$\hat{a}_y$, indexed by finite words y, we show explicit expressions for 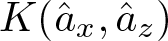$K(\hat{a}_x,\hat{a}_z)$, which is a finite sum. These values can be positive or negative depending on A and the words x and z. Words $x,z$ with large length can eventually produce large negative curvature 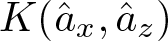$K(\hat{a}_x,\hat{a}_z)$. If 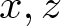$x, z$ do not begin with the same letter, then 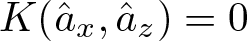$K(\hat{a}_x,\hat{a}_z)=0$.