Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T04:01:38.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Scattering for critical wave equations with variable coefficients

Part of: Hyperbolic equations and systems

Published online by Cambridge University Press:  30 April 2021

Shi-Zhuo Looi  and
Mihai Tohaneanu
Shi-Zhuo Looi
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, KY40506, USA ([email protected]; [email protected])
Mihai Tohaneanu
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, KY40506, USA ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that solutions to the quintic semilinear wave equation with variable coefficients in ${{\mathbb {R}}}^{1+3}$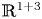 scatter to a solution to the corresponding linear wave equation. The coefficients are small and decay as $|x|\to \infty$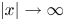, but are allowed to be time dependent. The proof uses local energy decay estimates to establish the decay of the $L^{6}$ 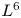norm of the solution as $t\to \infty$.

Keywords

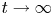scatteringdefocusingvariable coefficientsnonlinear wave equationhyperbolic equationpower-type nonlinearitypower-type non-linearitysemilinear wave equations

MSC classification

Primary: 35L05: Wave equation
Secondary: 35L71: Semilinear second-order hyperbolic equations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 298 - 316
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bahouri, H. and Gérard, P., High frequency approximation of solutions to critical nonlinear wave equations, Amer. J. Math. 121 (1999), 131–175.CrossRefGoogle Scholar
Bahouri, H. and Shatah, J., Decay estimates for the critical semilinear wave equation, Ann. Inst. H. Poincare Anal. Non Lineaire 15 (1998), 783–789.CrossRefGoogle Scholar
Burq, N., Lebeau, G. and Planchon, F., Global existence for energy critical waves in 3-D domains, J. Amer. Math. Soc. 21 (2008), 831–845.CrossRefGoogle Scholar
Duyckaerts, T. and Lafontaine, D., Scattering for critical radial Neumann waves outside a ball, arXiv:2004.08576.Google Scholar
Ginibre, J., Soffer, A. and Velo, G., The global Cauchy problem for the critical nonlinear wave equation, Jour. Func. Anal. 110 (1992), 96–130.CrossRefGoogle Scholar
Grillakis, M., A priori estimates and regularity of nonlinear waves, in Proceedings of the International Congress of Mathematicians, pp. 1187–1194 (Birkhauser, 1994).CrossRefGoogle Scholar
Grillakis, M., Regularity and asymptotic behavior of the wave equation with a critical nonlinearity, Ann. Math. 132 (1990), 485–509.CrossRefGoogle Scholar
Grillakis, M., Regularity for the wave equation with a critical nonlinearity, Comm. Pure Appl. Math. 45 (1992), 749–774.10.1002/cpa.3160450604CrossRefGoogle Scholar
Ibrahim, S. and Majdoub, M., Solutions globales de l'equation des ondes semilineaire critique ‘a coefficients variables, Bull. Soc. Math. France. (1) 131 (2003), 1–22.CrossRefGoogle Scholar
Jao, C., The quintic NLS on perturbations of ${{\mathbb {R}}}^{3}$, Amer. J. Math. 141 (2019), 981–1035.CrossRefGoogle Scholar
Jia, H., Liu, B. and Xu, G., Long time dynamics of defocusing energy critical $3 + 1$ dimensional wave equation with potential in the radial case, Comm. Math. Phys. 339(2) (2015), 353–384.CrossRefGoogle Scholar
Jia, H., Liu, B., Schlag, W. and Xu, G., Global center stable manifold for the defocusing energy critical wave equation with potential, Amer. J. Math. to appear.Google Scholar
Kapitanski, L., Global and unique weak solutions of nonlinear wave equations, Math. Res. Lett. 1 (1994), 211–223.CrossRefGoogle Scholar
Keel, M. and Tao, T., Endpoint Strichartz estimates, Amer. J. Math. 120 (1998), 955–980.CrossRefGoogle Scholar
Keel, M., Smith, H. and Sogge, C., Almost global existence for some semilinear wave equations, J. d'Anal. Math. 87 (2002), 265–279.CrossRefGoogle Scholar
Kenig, C. and Merle, F., Global well-posedness, scattering and blow-up for the energy-critical focusing non-linear wave equation, Acta Math. 201(2) (2008), 147–212.CrossRefGoogle Scholar
Killip, R., Visan, M. and Zhang, X., Quintic NLS in the exterior of a strictly convex obstacle, Amer. J. Math. 138 (2016), 1193–1346.CrossRefGoogle Scholar
Killip, R., Miao, C., Visan, M., Zhang, J. and Zheng, J., The energy-critical NLS with inverse- square potential, Discrete Contin. Dyn. Syst. 37(7) (2017), 3831–3866.CrossRefGoogle Scholar
Lafontaine, D., About the wave equation outside two strictly convex obstacles, arXiv:1711.09734.Google Scholar
Lai., N.-A. and Zhou, Y., Global existence of critical nonlinear wave equation with time dependent variable coefficients, Comm. Part. Diff. Equ. 11 (2012), 2171–2183.Google Scholar
Lawrie, A., Oh, S.-J. and Shahshahani, S., Profile decompositions for wave equations on hyperbolic space with applications, Math. Ann. 365(1–2) (2016), 707–803.CrossRefGoogle Scholar
Lindblad, H. and Rodnianski, I., The global stability of Minkowski space- time in harmonic gauge, Ann. Math. 171 (2010), 1401–1477.CrossRefGoogle Scholar
Metcalfe, J. and Sogge, C., Long-time existence of quasilinear wave equations exterior to star-shaped obstacles via energy methods, SIAM J. Math. Anal. 38 (2006), 188–209.10.1137/050627149CrossRefGoogle Scholar
Metcalfe, J. and Tataru, D., Decay estimates for variable coefficient wave equations in exterior domains, in Advances in phase space analysis of partial differential equations, Progr. Nonlinear Differential Equations Appl., 78, pp. 201–216 (2009).CrossRefGoogle Scholar
Metcalfe, J. and Tataru, D., Global parametrices and dispersive estimates for variable coefficient wave equations, Math. Ann. 353(4) (2012), 1183–1237.10.1007/s00208-011-0714-8CrossRefGoogle Scholar
Miao, C., Murphy, J. and Zheng, J., The energy-critical nonlinear wave equation with an inverse-square potential, Ann. Inst. H. Poincaré Anal. Non Linéaire 37(2) (2020), 417–456.CrossRefGoogle Scholar
Morawetz, C., Time decay for the nonlinear Klein-Gordon equation, Proc. Roy. Soc. Lon. 306 (1968), 291–296.Google Scholar
Nakanishi, K., Scattering theory for nonlinear Klein-Gordon equation with Sobolev critical power, Int. Math. Res. Not. 1 (1999), 31–60.CrossRefGoogle Scholar
Nakanishi, K., Unique global existence and asymptotic behaviour of solutions for wave equations with non-coercive critical nonlinearity, Comm. Partial Diff. Equ. 24 (1999), 185–221.CrossRefGoogle Scholar
Pecher, H., Nonlinear small data scattering for the wave and Klein-Gordon equations, Math. Z. 185 (1984), 261–270.CrossRefGoogle Scholar
Rauch, J., The $u^{5}$ Klein-Gordon equation. II. Anomalous singularities for semilinear wave equations, in Nonlinear partial differential equations and their applications. College de France Seminar, pp. 335–364, Research Notes in Mathematics, Volume 51 (Pitman Publ., 1981).Google Scholar
Shatah, J. and Struwe, M., Regularity results for nonlinear wave equations, Ann. Math. 138 (1993), 503–518.CrossRefGoogle Scholar
Shatah, J. and Struwe, M., Well-posedness in the energy space for semilinear wave equation with critical growth, Int. Math. Res. Not. 1994 (1994), 303–309.CrossRefGoogle Scholar
Smith, H. F. and Sogge, C. D., On the critical semilinear wave equation outside convex obstacles, J. Amer. Math. Soc. 8(4) (1995), 879–916.CrossRefGoogle Scholar
Sterbenz, J. and Rodnianski, I., Angular regularity and strichartz estimates for the wave equation, Int. Math. Res. Not. 4 (2005), 187–231.CrossRefGoogle Scholar
Struwe, M., Globally regular solutions to the $u^{5}$ Klein-Gordon equation, Ann. Scuola Norm. Sup. Pisa Cl. Sci. 15 (1988), 495–513.Google Scholar
Zhang, J. and Zheng, J., Scattering theory for nonlinear Schrödinger with inverse-square potential, J. Funct. Anal. 267 (2014), 2907–2932.CrossRefGoogle Scholar