No CrossRef data available.
Published online by Cambridge University Press: 04 June 2021
We say that a map $f$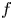 from a Banach space $X$
from a Banach space $X$ to another Banach space $Y$
to another Banach space $Y$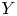 is a phase-isometry if the equality
is a phase-isometry if the equality
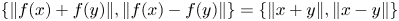
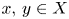 . A Banach space $X$
. A Banach space $X$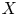 is said to have the Wigner property if for any Banach space $Y$
is said to have the Wigner property if for any Banach space $Y$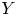 and every surjective phase-isometry $f : X\rightarrow Y$
and every surjective phase-isometry $f : X\rightarrow Y$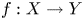 , there exists a phase function $\varepsilon : X \rightarrow \{-1,\,1\}$
, there exists a phase function $\varepsilon : X \rightarrow \{-1,\,1\}$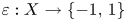 such that $\varepsilon \cdot f$
such that $\varepsilon \cdot f$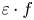 is a linear isometry. We present some basic properties of phase-isometries between two real Banach spaces. These enable us to show that all finite-dimensional polyhedral Banach spaces and CL-spaces possess the Wigner property.
is a linear isometry. We present some basic properties of phase-isometries between two real Banach spaces. These enable us to show that all finite-dimensional polyhedral Banach spaces and CL-spaces possess the Wigner property.
Please note a has been issued for this article.