Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T16:39:03.190Z Has data issue: false hasContentIssue false
  • English
  • Français

The Projective Leavitt Complex

Part of: Homological methods Representation theory of rings and algebras Abelian categories Homological algebra

Published online by Cambridge University Press:  15 August 2018

Huanhuan Li
Huanhuan Li*
Affiliation:
Centre for Research in Mathematics, Western Sydney University, Sydney, NSW 2150, Australia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For a finite quiver Q without sources, we consider the corresponding radical square zero algebra A. We construct an explicit compact generator for the homotopy category of acyclic complexes of projective A-modules. We call such a generator the projective Leavitt complex of Q. This terminology is justified by the following result: the opposite differential graded endomorphism algebra of the projective Leavitt complex of Q is quasi-isomorphic to the Leavitt path algebra of Qop. Here, Qop is the opposite quiver of Q, and the Leavitt path algebra of Qop is naturally 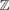${\open Z}$-graded and viewed as a differential graded algebra with trivial differential.

Keywords

Leavitt path algebraprojective Leavitt complexcompact generatordg quasi-balanced module

MSC classification

Primary: 16G20: Representations of quivers and partially ordered sets
Secondary: 16E45: Differential graded algebras and applications 18E30: Derived categories, triangulated categories 18G35: Chain complexes
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 4 , November 2018 , pp. 1155 - 1177
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Abrams, G. and Pino, G. Aranda, The Leavitt path algebra of a graph, J. Algebra 239 (2) (2005), 319–334.Google Scholar
2Abrams, G. and Pino, G. Aranda, Purely infinite simple Leavitt path algebras, J. Pure Appl. Algebra 207 (2006), 553–563.Google Scholar
3Abrams, G. and Rangaswamy, K. M., Regularity conditions for arbitrary Leavitt path algebras, Algebr. Represent. Theory 13(3) (2010), 319–334.Google Scholar
4Alahmadi, A., Alsulami, H., Jain, S. K. and Zelmanov, E., Leavitt path algebras of finite Gelfand-Kirillov dimension, J. Algebra Appl. 11(6) (2012), 6.Google Scholar
5Ara, P., Moreno, M. A. and Pardo, E., Nonstable K-theory for graph algebras, Algebr. Represent. Theory 10(2) (2007), 157–178.Google Scholar
6Pino, G. Aranda, Pardo, E. and Molina, M. Siles, Prime spectrum and primitive Leavitt path algebras, Indiana Univ. Math. J. 58(2) (2009), 869–890.Google Scholar
7Bökstedt, M. and Neeman, A., Homotopy limits in triangulated categories, Compositio Math. 86 (1993), 209–234.Google Scholar
8Buchweitz, R. O., 1987), Maximal Cohen-Macaulay modules and Tate cohomology over Gorenstein rings. Available at: http://hdl.handle.net/1807/16682.Google Scholar
9Chen, X. W., Irreducible representations of Leavitt path algebras, Forum Math. 27(1) (2015), 549–574.Google Scholar
10Chen, X. W. and Yang, D., Homotopy categories, Leavitt path algebras and Gorenstein projective modules, Inter. Math. Res. Not. 10 (2015), 2597–2633.Google Scholar
11Cuntz, J. and Krieger, W., A class of C*-algebras and topological Markov chains, Invent. Math. 63 (1981), 25–40.Google Scholar
12Jørgensen, P., The homotopy category of complexes of projective modules, Adv. Math. 193(1) (2005), 223–232.Google Scholar
13Keller, B., Deriving DG categories, Ann. Sci. École Norm. Sup. (4) 27(1) (1994), 63–102.Google Scholar
14Keller, B.. On the construction of triangle equivalences, Derived equivalences for group rings, Lecture Notes in Mathematics, Volume 1685 (Springer-Verlag, Berlin, 1998).Google Scholar
15Krause, H., The stable derived category of a Noetherian scheme, Compositio Math. 141 (2005), 1128–1162.Google Scholar
16Kumjian, A., Pask, D., Raeburn, I. and Renault, J., Graphs, groupoids, and Cuntz–Krieger algebras, J. Funct. Anal. 144 (1997), 505–541.Google Scholar
17Li, H. H., The injective Leavitt complex, Algebr. Represent. Theory 21(4) (2018), 833–858.Google Scholar
18Neeman, A., The Grothendieck duality theorem via Bousfield's techniques and Brown representability, J. Amer. Math. Soc. 9 (1996), 205–236.Google Scholar
19Neeman, A., The homotopy category of flat modules, and Grothendieck duality, Invent. Math. 174(2) (2008), 255–308.Google Scholar
20Orlov, D., Triangulated categories of singularities and D-branes in Landau-Ginzburg models, Trudy Steklov Math. Inst. 204 (2004), 240–262.Google Scholar
21Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras, Doc. Math. 5 (2000), 49–114.Google Scholar
22Raeburn, I., Graph algebras, CBMS Regional Conference Series, Volume 103 (Mathematics American Mathematical Society, Providence, RI, 2005).Google Scholar
23Smith, S. P., Category equivalences involving graded modules over path algebras of quivers, Adv. Math. 230 (2012), 1780–1810.Google Scholar
24Tomforde, M., Uniqueness theorems and ideal structure for Leavitt path algebras, J. Algebra 318 (2007), 270–299.Google Scholar