Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T19:43:59.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Operator equalities and Characterizations of Orthogonality in Pre-Hilbert C*-Modules

Part of: Selfadjoint operator algebras General theory of linear operators

Published online by Cambridge University Press:  17 June 2021

Rasoul Eskandari ,
M. S. Moslehian  and
Dan Popovici
Rasoul Eskandari
Affiliation:
Department of Mathematics, Faculty of Science, Farhangian University, Tehran, Iran ([email protected]) Department of Pure Mathematics, Center of Excellence in Analysis on Algebraic Structures (CEAAS), Ferdowsi University of Mashhad, P. O. Box 1159, Mashhad91775, Iran ([email protected])
M. S. Moslehian
Affiliation:
Department of Pure Mathematics, Center of Excellence in Analysis on Algebraic Structures (CEAAS), Ferdowsi University of Mashhad, P. O. Box 1159, Mashhad91775, Iran ([email protected])
Dan Popovici
Affiliation:
Department of Mathematics and Computer Science, West University of Timisoara, RO-300223Timisoara, Vasile Parvan Blvd no. 4, Romania ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In the first part of the paper, we use states on $C^{*}$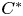-algebras in order to establish some equivalent statements to equality in the triangle inequality, as well as to the parallelogram identity for elements of a pre-Hilbert $C^{*}$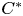-module. We also characterize the equality case in the triangle inequality for adjointable operators on a Hilbert $C^{*}$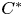-module. Then we give certain necessary and sufficient conditions to the Pythagoras identity for two vectors in a pre-Hilbert $C^{*}$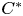-module under the assumption that their inner product has a negative real part. We introduce the concept of Pythagoras orthogonality and discuss its properties. We describe this notion for Hilbert space operators in terms of the parallelogram law and some limit conditions. We present several examples in order to illustrate the relationship between the Birkhoff–James, Roberts, and Pythagoras orthogonalities, and the usual orthogonality in the framework of Hilbert $C^{*}$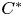-modules.

Keywords

Hilbert C*-modulenorm equalityPythagoras orthogonalityPythagoras identity

MSC classification

Primary: 46L08: $C^*$-modules 46L05: General theory of $C^*$-algebras
Secondary: 47A62: Equations involving linear operators, with operator unknowns
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 594 - 614
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramovich, Y. A., Aliprantis, C. D. and Burkinshaw, O., The Daugavet equation in uniformly convex Banach spaces, J. Funct. Anal. 97 (1991), 215–230.CrossRefGoogle Scholar
Arambašić, L.J. and Rajić, R., On some norm equalities in pre-Hilbert $C^{*}$-modules, Linear Algebra Appl. 414 (2006), 19–28.CrossRefGoogle Scholar
Arambašić, L. J. and Rajić, R., The Birkhoff-James orthogonality in Hilbert $C^{*}$-modules, Linear Algebra Appl. 437 (2012), 1913–1929.CrossRefGoogle Scholar
Arambašić, L. J. and Rajić, R., On symmetry of the (strong) Birkhoff–James orthogonality in Hilbert $C^{*}$-modules, Ann. Funct. Anal. 7 (2016), 17–23.CrossRefGoogle Scholar
Barraa, M. and Boumazgour, M., A lower bound of the norm of the operator $X\rightarrow AXB + BXA$, Extracta Math. 16 (2001), 223–227.Google Scholar
Barraa, M. and Boumazgour, M., Inner derivations and norm equality, Proc. Amer. Math. Soc. 130 (2002), 471–476.Google Scholar
Bhatia, R. and Šemrl, P., Orthogonality of matrices and some distance problems, Linear Algebra Appl. 287 (1999), 77–85.CrossRefGoogle Scholar
Bhattacharyya, T. and Grover, P., Characterization of Birkhoff-James orthogonality, J. Math. Anal. Appl. 407 (2013), 350–358.CrossRefGoogle Scholar
Birkhoff, G., Orthogonality in linear metric spaces, Duke Math. J. 1 (1935), 169–172.10.1215/S0012-7094-35-00115-6CrossRefGoogle Scholar
Feldman, I., Krupnik, N. and Markus, A., On the norm of polynomials of two adjoint projections, Integral Eq. Oper. Theory 14 (1991), 70–90.Google Scholar
James, R. C., Orthogonality in normed linear spaces, Duke Math. J. 12 (1945), 291–302.Google Scholar
James, R. C., Orthogonality and linear functionals in normed linear spaces, Trans. Amer. Math. Soc. 61 (1947), 265–292.Google Scholar
Kittaneh, F., Norm inequalities for sums of positive operators, J. Oper. Theory 48 (2002), 95–103.Google Scholar
Lance, E. C., Hilbert C*-modules: A toolkit for operator algebraists, (Cambridge University Press, Oxford, 1995).10.1017/CBO9780511526206CrossRefGoogle Scholar
Magajna, B., On the distance to finite-dimensional subspaces in operator algebras, J. London Math. Soc. 47 (1993), 516–532.CrossRefGoogle Scholar
Moslehian, M. S. and Zamani, A., Characterizations of operator Birkhoff–James orthogonality, Canad. Math. Bull. 60 (2017), 816–829.CrossRefGoogle Scholar
Murphy, G. J., C*-Algebras and Operator Theory, (Academic Press, New York, 1990).Google Scholar
Nakamoto, R. and Takahasi, S.-E., Norm equality condition in triangular inequality, Sci. Math. Japonicae 8 (2001), 367–370.Google Scholar
Popovici, D., Norm equalities in pre-Hilbert $C^{*}$-modules, Linear Algebra Appl. 436 (2012), 59–70.CrossRefGoogle Scholar
Roberts, B. D., On the geometry of abstract vector spaces, Tôhoku Math. J. 39 (1934), 42–59.Google Scholar