Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-29T01:15:21.146Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Range Inclusion for Normal Derivations on C*-algebras

Part of: Special classes of linear operators Selfadjoint operator algebras

Published online by Cambridge University Press:  22 February 2017

Bojan Magajna
Bojan Magajna*
Affiliation:
Department of Mathematics, University of Ljubljana, Jadranska 21, Ljubljana 1000, Slovenia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For a von Neumann subalgebra 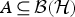$A \, \subseteq \, {\cal B}({\cal H})$ and any two elements a, b ∈ A with a normal, such that the corresponding derivations da and db satisfy the condition ‖db(x)‖ ≤ ‖da(x)‖ for all x ∈ A, there exist completely bounded (a)ʹ-bimodule map 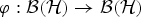$\varphi : {\cal B}({\cal H}) \rightarrow {\cal B}({\cal H})$ such that db|A = φ da|A=daφ|A. (In particular db(A) ⊆ da(A).) Moreover, if A is a factor, then φ can be taken to be normal and these equalities hold on 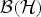${\cal B}({\cal H})$ instead of just on A. This result is not true for general (even primitive) C*-algebras 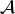${\cal A}$.

Keywords

C*-algebraderivationcompletely bounded map

MSC classification

Primary: 46L57: Derivations, dissipations and positive semigroups in $C^*$-algebras 47B47: Commutators, derivations, elementary operators, etc.
Secondary: 47B15: Hermitian and normal operators (spectral measures, functional calculus, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 1 , February 2018 , pp. 1 - 11
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Aleksandrov, A. B., Peller, V. V., Potapov, D. and Sukochev, F., Functions of normal operators under perturbations, Adv. Math. 226 (2011), 5216–5251.Google Scholar
2 Ara, P. and Mathieu, M., Local multipliers of C*-algebras, Springer Monographs in Mathematics (Springer, 2003).Google Scholar
3 Archbold, R. J., Kaniuth, E. and Somerset, D. W. B., Norms of inner derivations for multiplier algebras of C*-algebras and group C*-algebras II, Adv. Math. 280 (2015), 225–255.Google Scholar
4 Bonsall, F. F. and Duncan, J., Complete Normed Algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete Volume 80 (Springer, 1973).Google Scholar
5 Brešar, M., The range and kernel inclusion of algebraic derivations and commuting maps, Q. J. Math. 56 (2005), 31–41.Google Scholar
6 Brešar, M., Magajna, B. and Špenko, S., Identifying derivations through the spectra of their values, Integ. Eqns Operat. Theory 73, (2012), 395–411.Google Scholar
7 Elliott, G. A. and Zsido, L., Almost uniformly continuous automorphism groups of operator algebras, J. Operat. Theory 8 (1982), 227–277.Google Scholar
8 Fong, C. K., Range inclusion for normal derivations, Glasgow Math. J. 25 (1984), 255–262.Google Scholar
9 Glimm, J., A Stone-Weierstrass theorem for C*-algebras, Ann. Math. 72 (1960), 216–244.Google Scholar
10 Halpern, H., Irreducible module homomorphisms of a von Neumann algebra into its center, Trans. Am. Math. Soc. 140 (1969), 195–221.Google Scholar
11 Ho, Y., Commutants and derivation ranges, Tohoku Math. J. 27 (1975), 509–514.Google Scholar
12 Johnson, B. E. and Williams, J.P., The range of a normal derivation, Pac. J. Math. 58 (1975), 105–122.Google Scholar
13 Kissin, E. and Shulman, V. S., On the range inclusion of normal derivations: variations on a theme by Johnson, Williams and Fong, Proc. Lond. Math. Soc. 83 (2001), 176–198.Google Scholar
14 Kissin, E. and Shulman, V. S., Classes of operator smooth functions, I, operator Lipschitz functions, Proc. Edinb. Math. Soc. 48 (2005), 151–173.Google Scholar
15 Magajna, B., The Haagerup norm on the tensor product of operator modules, J. Funct. Analysis 129 (1995), 325–348.Google Scholar
16 Magajna, B., Variance of operators and derivations, J. Math. Analysis Applic. 433 (2016), 1–30.Google Scholar
17 Murphy, G. J., C*-algebras and operator theory (Academic Press, 1990).Google Scholar
18 Paulsen, V. I., Completely bounded maps and operator algebras, Cambridge Studies in Advanced Mathematics, Volume 78 (Cambridge University Press, 2002).Google Scholar
19 Pedersen, G. K., C*-algebras and their automorphism groups (Academic Press, 1979).Google Scholar
20 Sinclair, A. M. and Roger Smith, R., Hochschild cohomology of von Neumann algebras, London Mathematical Society Lecture Notes Series, Volume 203 (Cambridge Universit Press, 1995).Google Scholar
21 Smith, R. R., Completely bounded module maps and the Haagerup tensor product, J. Funct. Analysis 102 (1991), 156–175.Google Scholar