Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T08:40:31.306Z Has data issue: false hasContentIssue false
  • English
  • Français

On the adjoint representation of a hopf algebra

Part of: Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  11 November 2020

Stefan Kolb ,
Martin Lorenz ,
Bach Nguyen  and
Ramy Yammine
Stefan Kolb
Affiliation:
School of Mathematics, Statistics and Physics, Newcastle University, NewcastleNE1 7RU, UK
Martin Lorenz
Affiliation:
Department of Mathematics, Temple University, Philadelphia, PA19122, USA ([email protected])
Bach Nguyen
Affiliation:
Department of Mathematics, Xavier University of Louisiana, New Orleans, LA70125, USA
Ramy Yammine
Affiliation:
Department of Mathematics, Temple University, Philadelphia, PA19122, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the adjoint representation of a Hopf algebra $H$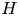 focusing on the locally finite part, $H_{{\textrm ad\,fin}}$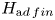, defined as the sum of all finite-dimensional subrepresentations. For virtually cocommutative $H$ 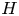(i.e., $H$ 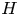is finitely generated as module over a cocommutative Hopf subalgebra), we show that $H_{{\textrm ad\,fin}}$ 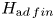is a Hopf subalgebra of $H$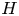. This is a consequence of the fact, proved here, that locally finite parts yield a tensor functor on the module category of any virtually pointed Hopf algebra. For general Hopf algebras, $H_{{\textrm ad\,fin}}$ is shown to be a left coideal subalgebra. We also prove a version of Dietzmann's Lemma from group theory for Hopf algebras.

Keywords

Infinite-dimensional Hopf algebracocommutative Hopf algebrapointed Hopf algebraHopf subalgebraadjoint representationlocally finite parttensor functorcoideal subalgebraΔ-methodsDietzmann's Lemma

MSC classification

Primary: 16T05: Hopf algebras and their applications
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 4 , November 2020 , pp. 1092 - 1099
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergen, J., Adjoint actions of cocommutative Hopf algebras, pp. 25–34, Groups, Rings and Algebras, Contemp. Math., Volume 420 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Bergen, J. and Passman, D. S., Delta methods in enveloping rings, J. Algebra 133(2) (1990), 277–312.CrossRefGoogle Scholar
Bergen, J. and Passman, D. S., Delta methods in enveloping algebras of Lie superalgebras, Trans. Am. Math. Soc. 334(1) (1992), 259–280.CrossRefGoogle Scholar
Bergen, J. and Passman, D. S., Delta methods in enveloping rings. II, J. Algebra 156(2) (1993), 494–534.CrossRefGoogle Scholar
Bourbaki, N., Algèbre. Chapitres 1 à 3 (Hermann, Paris, 1970).Google Scholar
Brown, K. A. and Goodearl, K. R., Lectures on algebraic quantum groups, Advanced Courses in Mathematics (CRM Barcelona, Birkhäuser Verlag, Basel, 2002).CrossRefGoogle Scholar
Dietzmann, A. P., On $p$-groups, Dokl. Akad. Nauk SSSR 15 (1937), 71–76.Google Scholar
Hopf, H., Über die Topologie der Gruppen-Mannigfaltigkeiten und ihre Verallgemeinerungen, Ann. Math. (2) 42 (1941), 22–52.CrossRefGoogle Scholar
Joseph, A. and Letzter, G., Separation of variables for quantized enveloping algebras, Am. J. Math. 116(1) (1994), 127–177.CrossRefGoogle Scholar
Kurosh, A. G., The theory of groups, Volume II (Chelsea Publishing Company, New York, NY, 1956). Translated from the Russian and edited by K. A. Hirsch.Google Scholar
Letzter, G., Coideal subalgebras and quantum symmetric pairs, pp. 117–165, New directions in Hopf algebras, Math. Sci. Res. Inst. Publ., Volume 43 (Cambridge University Press, Cambridge, 2002).Google Scholar
Lorenz, M., A tour of representation theory, Graduate Studies in Mathematics, Volume 193 (American Mathematical Society, Providence, RI, 2018).CrossRefGoogle Scholar
Masuoka, A., On Hopf algebras with cocommutative coradicals, J. Algebra 144(2) (1991), 451–466.CrossRefGoogle Scholar
Montgomery, S., Hopf algebras and their actions on rings, CBMS Regional Conference Series in Mathematics, Volume 82 (Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1993).CrossRefGoogle Scholar
Passman, D. S., The algebraic structure of group rings, Pure and Applied Mathematics (Wiley-Interscience [John Wiley & Sons], New York, NY, 1977).Google Scholar
Radford, D. E., Hopf algebras, Series on Knots and Everything, Volume 49 (World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2012).Google Scholar
Sweedler, M. E., Hopf algebras, Mathematics Lecture Note Series (W. A. Benjamin, Inc., New York, NY, 1969).Google Scholar