No CrossRef data available.
Article contents
Mean values of multiplicative functions and applications to residue-class distribution
Published online by Cambridge University Press: 10 February 2025
Abstract
We provide a uniform bound on the partial sums of multiplicative functions under very general hypotheses. As an application, we give a nearly optimal estimate for the count of 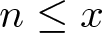 $n \le x$ for which the Alladi–Erdős function
$n \le x$ for which the Alladi–Erdős function 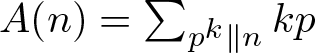 $A(n) = \sum_{p^k \parallel n} k p$ takes values in a given residue class modulo q, where q varies uniformly up to a fixed power of
$A(n) = \sum_{p^k \parallel n} k p$ takes values in a given residue class modulo q, where q varies uniformly up to a fixed power of  $\log x$. We establish a similar result for the equidistribution of the Euler totient function
$\log x$. We establish a similar result for the equidistribution of the Euler totient function 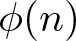 $\phi(n)$ among the coprime residues to the ‘correct’ moduli q that vary uniformly in a similar range and also quantify the failure of equidistribution of the values of
$\phi(n)$ among the coprime residues to the ‘correct’ moduli q that vary uniformly in a similar range and also quantify the failure of equidistribution of the values of 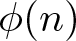 $\phi(n)$ among the coprime residue classes to the ‘incorrect’ moduli.
$\phi(n)$ among the coprime residue classes to the ‘incorrect’ moduli.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.



