Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T14:27:16.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Graded identities for algebras with elementary gradings over an infinite field

Part of: Rings and algebras with additional structure Basic linear algebra Rings with polynomial identity

Published online by Cambridge University Press:  10 January 2022

Diogo Diniz Open the ORCID record for Diogo Diniz [Opens in a new window] ,
Claudemir Fidelis Open the ORCID record for Claudemir Fidelis [Opens in a new window]  and
Plamen Koshlukov
Diogo Diniz
Affiliation:
Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, Campina Grande, PB58429-970, Brazil ([email protected], [email protected])
Claudemir Fidelis
Affiliation:
Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, Campina Grande, PB58429-970, Brazil ([email protected], [email protected]) Instituto de Matemática e Estatística da Universidade de São Paulo, São Paulo, SP05508-090, Brazil
Plamen Koshlukov
Affiliation:
Department of Mathematics, UNICAMP, 13083-859Campinas, SP, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $F$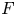 be an infinite field of positive characteristic $p > 2$ 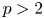and let $G$ 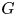be a group. In this paper, we study the graded identities satisfied by an associative algebra equipped with an elementary $G$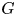-grading. Let $E$ 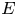be the infinite-dimensional Grassmann algebra. For every $a$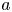, $b\in \mathbb {N}$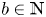, we provide a basis for the graded polynomial identities, up to graded monomial identities, for the verbally prime algebras $M_{a,b}(E)$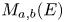, as well as their tensor products, with their elementary gradings. Moreover, we give an alternative proof of the fact that the tensor product $M_{a,b}(E)\otimes M_{r,s}(E)$ 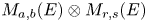and $M_{ar+bs,as+br}(E)$ 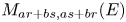are $F$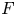-algebras which are not PI equivalent. Actually, we prove that the $T_{G}$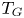-ideal of the former algebra is contained in the $T$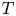-ideal of the latter. Furthermore, the inclusion is proper. Recall that it is well known that these algebras satisfy the same multilinear identities and hence in characteristic 0 they are PI equivalent.

Keywords

graded identitymatrices over Grassmann algebrasPI equivalenceelementary grading

MSC classification

Primary: 15A75: Exterior algebra, Grassmann algebras 16R10: $T$-ideals, identities, varieties of rings and algebras
Secondary: 16R50: Other kinds of identities (generalized polynomial, rational, involution) 16W50: Graded rings and modules
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 146 - 166
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aljadeff, E. and Ofir, D., On regular $G$-gradings, Trans. Amer. Math. Soc. 367(6) (2015), 4207–4233.CrossRefGoogle Scholar
Alves, S. M., PI (non) equivalence and Gelfand-Kirillov dimension in positive characteristic, Rend. Circ. Mat. Palermo (2) 58(1) (2009), 109–124.CrossRefGoogle Scholar
Alves, S. M. and Koshlukov, P., Polynomial identities of algebras in positive characteristic, J. Algebra 305(2) (2006), 1149–1165.CrossRefGoogle Scholar
Azevedo, S. S., Graded identities for the matrix algebra of order $n$ over an infinite field, Commun. Algebra 30(12) (2002), 5849–5860.CrossRefGoogle Scholar
Azevedo, S. S., Fidelis, M. and Koshlukov, P., Tensor product theorems in positive characteristic, J. Algebra 276(2) (2004), 836–845.CrossRefGoogle Scholar
Azevedo, S. S., Fidelis, M. and Koshlukov, P., Graded identities and PI equivalence of algebras in positive characteristic, Commun. Algebra 33 (2005), 1011–1022.CrossRefGoogle Scholar
Bahturin, Y. and Drensky, V., Graded polynomial identities of matrices, Linear Algebra Appl. 357(1-3) (2002), 15–34.CrossRefGoogle Scholar
Bahturin, Yu. A., Mikhalev, A. A., Petrogradsky, V. M. and Zaicev, M. Z., Infinite Dimensional Lie Superalgebras, De Gruyter Expo. Math. Vol. 7 (Walter De Gruyter & Co., Berlin, 1992).CrossRefGoogle Scholar
Bemm, L., Fornaroli, E. Z. and Santulo, E. A. Jr., A cohomological point of view on gradings on algebras with multiplicative basis, J. Pure Appl. Algebra 223(2) (2019), 769–782.CrossRefGoogle Scholar
Berele, A., Generic verbally prime algebras and their GK-dimensions, Comm. Algebra 21(5) (1993), 1487–1504.CrossRefGoogle Scholar
Berele, A., Invariant theory and trace identities associated with Lie color algebras, J. Algebra 310 (2007), 194–206.CrossRefGoogle Scholar
Centrone, L., Diniz, D. and de Mello, T. C., Graded monomial identities and almost non-degenerate gradings on matrices, preprint arXiv:2001.00489v3 (2020).Google Scholar
Di Vincenzo, O. M., On the graded identities of $M_{1,1}(E)$, Israel J. Math. 80(3) (1992), 323–335.CrossRefGoogle Scholar
Di Vincenzo, O. M. and da Silva, V. R. T., On $\mathbb {Z}_2$-graded polynomial identities of the Grassmann algebra, Linear Algebra Appl. 431(1-2) (2009), 56–72.CrossRefGoogle Scholar
Di Vincenzo, O. M. and Nardozza, V., $\mathbb {Z}_{k+l}\times \mathbb {Z}_2$-graded polynomial identities for $M_{k,l}(E)\otimes E$, Rend. Sem. Mat. Univ. Padova 108 (2002), 27–39.Google Scholar
Di Vincenzo, O. M. and Nardozza, V., Graded polynomial identities for tensor products by the Grassmann algebra, Comm. Algebra 31(3) (2003), 1453–1474.CrossRefGoogle Scholar
Di Vincenzo, O. M. and Nardozza, V., Graded polynomial identities of verbally prime algebras, J. Algebra Appl. 6(3) (2007), 385–401.CrossRefGoogle Scholar
Di Vincenzo, O. M., Koshlukov, P. and Santulo, E. A., Graded identities for tensor products of matrix (super)algebras over the Grassmann algebra, Linear Algebra Appl. 432(2–3) (2010), 780–795.CrossRefGoogle Scholar
Diniz, D. and de Mello, T., Graded identities of block-triangular matrices, J. Algebra 464 (2016), 246–265.Google Scholar
Fidelis, C., Diniz, D., Bernardo, L. and Koshlukov, P., Graded identities and central polynomials for the verbally prime algebras, to appearGoogle Scholar
Giambruno, A. and Zaicev, M., Polynomial Identities and Asymptotic Methods, Math. Surveys Monogr., Vol. 122 (Amer. Math. Soc., Providence, RI, 2005).CrossRefGoogle Scholar
Guimarães, A. A. and Koshlukov, P., Automorphisms and superalgebra structures on the Grassmann algebra, preprint arXiv :2009.00175v1, 2020.Google Scholar
Kemer, A. R., Varieties and $\mathbb {Z}_2$-graded algebras, Izv. Akad. Nauk SSSR Ser. Mat. 48(5) (1984), 1042–1059.Google Scholar
Kemer, A. R., Ideals of identities of associative algebras. Translations Math. Monographs, Vol. 87 (Providence, RI: Amer. Math. Soc, 1991).Google Scholar
Kemer, A. R., Remarks on the prime varieties, Israel J. Math. 96, Pt. B (1996), 341–356.CrossRefGoogle Scholar
Koshlukov, P. and Azevedo, S. S., Graded identities for T-prime algebras over fields of positive characteristic, Israel J. Math. 128 (2002), 157–176.CrossRefGoogle Scholar
Razmyslov, Yu. P., Identities of algebras and their representations, Transl. Math. Monographs, Vol. 138 (Providence, RI: Amer. Math. Soc., 1994).CrossRefGoogle Scholar
Regev, A., Tensor products of matrix algebras over the Grassmann algebra, J. Algebra 133(2) (1990), 512–526.CrossRefGoogle Scholar
Regev, A. and Seeman, T., $\mathbb {Z}_2$-graded tensor product of p.i. algebras, J. Algebra 291(1) (2005), 274–296.CrossRefGoogle Scholar
Vasilovsky, S.Yu., Z-graded polynomial identities of the full matrix algebra, Commun. Algebra 26(2) (1998), 601–612.CrossRefGoogle Scholar
Vasilovsky, S.Yu., $\mathbb {Z}_n$-graded polynomial identities of the full matrix algebra of order $n$, Proc. Amer. Math. Soc. 127(12) (1999), 3517–3524.CrossRefGoogle Scholar