No CrossRef data available.
Article contents
Free rank of symmetry of products of Dold manifolds
Published online by Cambridge University Press: 30 March 2023
Abstract
Dold manifolds 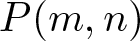 $P(m,n)$ are certain twisted complex projective space bundles over real projective spaces and serve as generators for the unoriented cobordism algebra of smooth manifolds. The paper investigates the structure of finite groups that act freely on products of Dold manifolds. It is proved that if a finite group G acts freely and
$P(m,n)$ are certain twisted complex projective space bundles over real projective spaces and serve as generators for the unoriented cobordism algebra of smooth manifolds. The paper investigates the structure of finite groups that act freely on products of Dold manifolds. It is proved that if a finite group G acts freely and 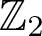 $ \mathbb{Z}_2 $ cohomologically trivially on a finite CW-complex homotopy equivalent to
$ \mathbb{Z}_2 $ cohomologically trivially on a finite CW-complex homotopy equivalent to 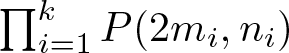 ${\prod_{i=1}^{k} P(2m_i,n_i)}$, then
${\prod_{i=1}^{k} P(2m_i,n_i)}$, then 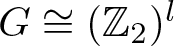 $G\cong (\mathbb{Z}_2)^l$ for some
$G\cong (\mathbb{Z}_2)^l$ for some 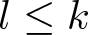 $l\leq k$ (see Theorem A for the exact bound). We also determine some bounds in the case when for each i, ni is even and mi is arbitrary. As a consequence, the free rank of symmetry of these manifolds is determined for cohomologically trivial actions.
$l\leq k$ (see Theorem A for the exact bound). We also determine some bounds in the case when for each i, ni is even and mi is arbitrary. As a consequence, the free rank of symmetry of these manifolds is determined for cohomologically trivial actions.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 1 , February 2023 , pp. 117 - 132
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.



