Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T08:32:48.600Z Has data issue: false hasContentIssue false
  • English
  • Français

A Fractal Operator on Some Standard Spaces of Functions

Part of: Nonlinear operators and their properties Numerical approximation and computational geometry Calculus on manifolds; nonlinear operators General theory of linear operators Classical measure theory

Published online by Cambridge University Press:  10 January 2017

P. Viswanathan  and
M. A. Navascués
P. Viswanathan
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, ACT 2601, Australia
M. A. Navascués
Affiliation:
Departmento de Matemática Aplicada, Escuela de Ingeniería y Arquitectura, Universidad de Zaragoza, C/ María de Luna 3, Zaragoza 50018, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

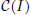Through appropriate choices of elements in the underlying iterated function system, the methodology of fractal interpolation enables us to associate a family of continuous self-referential functions with a prescribed real-valued continuous function on a real compact interval. This procedure elicits what is referred to as an α-fractal operator on , the space of all real-valued continuous functions defined on a compact interval I. With an eye towards connecting fractal functions with other branches of mathematics, in this paper we continue to investigate the fractal operator in more general spaces such as the space 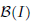of all bounded functions and the Lebesgue space 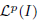, and in some standard spaces of smooth functions such as the space 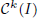of k-times continuously differentiable functions, Hölder spaces 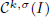and Sobolev spaces 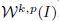. Using properties of the α-fractal operator, the existence of Schauder bases consisting of self-referential functions for these function spaces is established.

Keywords

fractal functionsfractal operatorfunction spacestopological isomorphismSchauder basis

MSC classification

Secondary: 28A80: Fractals 65D05: Interpolation 47A05: General (adjoints, conjugates, products, inverses, domains, ranges, etc.) 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc. 58C05: Real-valued functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 3 , August 2017 , pp. 771 - 786
Copyright
Copyright © Edinburgh Mathematical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Barnsley, M. F., Fractal functions and interpolation, Constr. Approx. 2 (1986), 303–329.Google Scholar
2. Barnsley, M. F. and Harrington, A. N., The calculus of fractal interpolation functions, J. Approx. Theory 57(1) (1989), 14–34.Google Scholar
3. Barnsley, M. F. and Massopust, P., Bilinear fractal interpolation and box dimension, J. Approx. Theory 192 (2015), 362–378.CrossRefGoogle Scholar
4. Barnsley, M. F., Hegland, M. and Massopust, P., Numerics and fractals, Bull. Inst. Math. Acad. Sin. 9(3) (2014), 389–430.Google Scholar
5. Conway, J. B., A course in functional analysis, 2nd edn (Springer, 1996).Google Scholar
6. Evans, L. C., Partial differential equations, 1st edn (American Mathematical Society, Providence, RI, 1998).Google Scholar
7. Feng, Z. G., Feng, Y. Z. and Yuan, Z. Y., Fractal interpolation surfaces with function vertical scaling factors, Appl. Math. Lett. 25(11) (2012), 1896–1900.Google Scholar
8. Fučík, S., Fredholm alternative for nonlinear operators in Banach spaces and its applications to differential and integral equations, Čas Pro Pěst. Mat. 96 (1971), 371–390.Google Scholar
9. Massopust, P., Fractal functions, fractal surfaces, and wavelets (Academic Press, 1995).Google Scholar
10. Massopust, P., Fractal functions and their applications. Chaos, Solitons & Fractals 8(2) (1997), 171–190.Google Scholar
11. Massopust, P., Fractal functions, splines, and Besov and Triebel–Lizorkin spaces, in Fractals in engineering: new trends and applications, ed. Lévy-Véhel, J. and Lutton, E., pp. 21–32 (Springer, 2005).Google Scholar
12. Massopust, P., Local fractal functions and function spaces, Springer Proceedings in Mathematics & Statistics: Fractals, Wavelets, and Their Applications, Volume 92, pp. 245–270 (Springer, 2014).Google Scholar
13. Massopust, P., On local fractal functions in Banach spaces, AIP Conf. Proc. 1648 (2015), 640002-01–640002-04.CrossRefGoogle Scholar
14. Navascués, M. A., Fractal polynomial interpolation, Z. Analysis Anwend. 25(2) (2005), 401–418.CrossRefGoogle Scholar
15. Navascués, M. A., Fractal approximation, Complex Analysis Operat. Theory 4(4) (2010), 953–974.Google Scholar
16. Navascués, M. A., Fractal Haar sytem, Nonlin. Analysis TMA 74 (2011), 4152–4165.Google Scholar
17. Navascués, M. A., Fractal bases of Lp spaces, Fractals 20 (2012), 141–148.Google Scholar
18. Navascués, M. A. and Sebastián, M. V., Smooth fractal interpolation, J. Inequal. Applicat. 2006 (2006), 78734.Google Scholar
19. Ramm, A. G., A simple proof of the Fredholm alternative and a characterization of the Fredholm operators, Am. Math. Mon. 108(9) (2001), 855–860.Google Scholar
20. Triebel, H., Theory of function spaces (Birkhäuser, 1983).CrossRefGoogle Scholar
21. Triebel, H., Theory of function spaces II (Birkhäuser, 1992).Google Scholar
22. Viswanathan, P., Chand, A. K. B. and Navascués, M. A., Fractal perturbation preserving fundamental shapes: bounds on the scale factors, J. Math. Analysis Applic. 419 (2014), 804–817.Google Scholar
23. Viswanathan, P., Navascués, M. A. and Chand, A. K. B., Fractal polynomials and maps in approximation of continuous functions, Numer. Func. Analysis Optim. 37(1) (2015), http://doi.org/brvp.Google Scholar
24. Viswanathan, P., Navascués, M. A. and Chand, A. K. B., Associate fractal functions in -spaces and in one-sided uniform approximation, J. Math. Analysis Applic. 433(2) (2015), 862–876.Google Scholar
25. Wang, H. Y. and Yu, J. S., Fractal interpolation functions with variable parameters and their analytical properties, J. Approx. Theory 175 (2013), 1–18.Google Scholar