Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T17:51:41.639Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Groups and Lie Rings with an Automorphism of Order 2n

Part of: Representation theory of groups Special aspects of infinite or finite groups Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  15 June 2016

E. I. Khukhro ,
N. Yu. Makarenko  and
P. Shumyatsky
E. I. Khukhro
Affiliation:
Sobolev Institute of Mathematics, Novosibirsk, 630 090, Russia ([email protected]; [email protected]) University of Lincoln, Brayford Pool, Lincoln LN6 7TS, UK
N. Yu. Makarenko
Affiliation:
Sobolev Institute of Mathematics, Novosibirsk, 630 090, Russia ([email protected]; [email protected])
P. Shumyatsky
Affiliation:
Department of Mathematics, University of Brasilia, DF 70910-900, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that a finite group G admits an automorphism 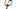of order 2n such that the fixed-point subgroup 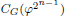of the involution 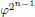is nilpotent of class c. Let m = 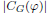) be the number of fixed points of 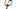. It is proved that G has a characteristic soluble subgroup of derived length bounded in terms of n, c whose index is bounded in terms of m, n, c. A similar result is also proved for Lie rings.

Keywords

finite groupLie ringderived lengthFitting heightnilpotency classautomorphism

MSC classification

Secondary: 20D45: Automorphisms 17B40: Automorphisms, derivations, other operators 20F40: Associated Lie structures 20F50: Periodic groups; locally finite groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 2 , May 2017 , pp. 391 - 412
Copyright
Copyright © Edinburgh Mathematical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)