Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-24T15:01:08.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Convolution structures for an Orlicz space with respect to vector measures on a compact group

Part of: Abstract harmonic analysis Measures, integration, derivative, holomorphy

Published online by Cambridge University Press:  26 March 2021

Manoj Kumar  and
N. Shravan Kumar
Manoj Kumar
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, New Delhi110016, India ([email protected]; [email protected])
N. Shravan Kumar
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, New Delhi110016, India ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to present some results about the space $L^{\varPhi }(\nu ),$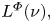 where $\nu$ 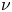is a vector measure on a compact (not necessarily abelian) group and $\varPhi$ 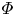is a Young function. We show that under natural conditions, the space $L^{\varPhi }(\nu )$ 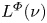becomes an $L^{1}(G)$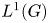-module with respect to the usual convolution of functions. We also define one more convolution structure on $L^{\varPhi }(\nu ).$

Keywords

Compact groupOrlicz spacevector measureconvolution

MSC classification

Primary: 43A77: Analysis on general compact groups 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc.
Secondary: 46G10: Vector-valued measures and integration
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 1 , February 2021 , pp. 87 - 98
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Calabuig, J. M., Galaz-Fontes, F., Navarrete, E. M. and Sánchez-Pérez, E. A., Fourier transforms and convolutions on $L^{p}$ of a vector measure on a compact Haussdorff abelian group, J. Fourier Anal. Appl. 19 (2013), 312–332.CrossRefGoogle Scholar
Delgado, O., Banach function subspaces of $L^{1}$ of a vector measure and related Orlicz spaces, Indag. Math., N.S. 15(4) (2004), 485–495.CrossRefGoogle Scholar
Delgado, O. and Miana, P., Algebra structure for $L^{p}$ of a vector measure, J. Math. Anal. Appl. 358(2) (2009), 355–363.CrossRefGoogle Scholar
Diestel, J. and Uhl, J. J., Vector measures, Mathematical Surveys, Volume 15 (American Mathematical Society, Providence, 1977).Google Scholar
Ferrando, I. and Galaz-Fontes, F., Multiplication operators on vector measure Orlicz spaces, Indag. Math., N.S. 20(1) (2009), 57–51.CrossRefGoogle Scholar
Folland, G. B., A course in abstract harmonic analysis (CRC Press, Boca Raton, 1995).Google Scholar
Kakutani, S., Two fixed-point theorems concerning bicompact convex sets, Proc. Imp. Acad. Japan 14 (1938), 242–245.Google Scholar
Krasnosel'skii, M. A. and Rutickii, Ya. B., Convex functions and Orlicz spaces (P. Noordhoff Ltd., Groningen, 1961).Google Scholar
Okada, S., Ricker, W. J. and Sánchez Pérez, E. A., Optimal domain and integral extension of operators acting in function spaces, Operator Theory: Advances and Applications, Volume 180 (Birkhäuser, Basel, 2008).Google Scholar
Rao, M. M. and Ren, Z. D., Theory of Orlicz spaces (Dekker, New York, 1991).Google Scholar