Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-23T09:31:34.377Z Has data issue: false hasContentIssue false
  • English
  • Français

The abelianization of the elementary group of rank two

Part of: Steinberg groups and $K_2$

Published online by Cambridge University Press:  20 January 2025

Behrooz Mirzaii Open the ORCID record for Behrooz Mirzaii [Opens in a new window]  and
Elvis Torres Pérez Open the ORCID record for Elvis Torres Pérez [Opens in a new window]
Behrooz Mirzaii
Affiliation:
Instituto de Ciências Matemáticas e de Computação (ICMC), Universidade de São Paulo, São Carlos, Brazil
Elvis Torres Pérez*
Affiliation:
Factultad de Ciencias, Universidad Nacional de Ingeniería (UNI), Lima, Perú
*
Corresponding author: Elvis Torres Pérez, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For an arbitrary ring A, we study the abelianization of the elementary group 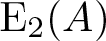$\mathit{{\rm E}}_2(A)$. In particular, we show that for a commutative ring A there exists an exact sequence

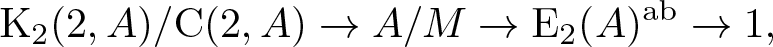\begin{equation*}{\rm K}_2(2,A)/{\rm C}(2,A) \rightarrow A/M \rightarrow \mathit{{\rm E}}_2(A)^{\rm ab} \rightarrow 1,\end{equation*}

where 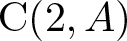${\rm C}(2,A)$ is the central subgroup of the Steinberg group 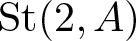$\mathit{{\rm St}}(2,A)$ generated by the Steinberg symbols and M is the additive subgroup of A generated by 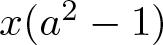$x(a^2-1)$ and 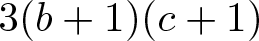$3(b+1)(c+1)$, with 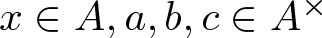$x\in A, a,b,c \in {A^\times}$.

Keywords

algebraic K-theorygroup homologySteinberg symbols

MSC classification

Primary: 19C99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adem, A. and Naffah, N., On the cohomology of $\mathit{{{\rm} SL}}_2(\mathbb{Z}[1/p])$. London Math. Soc. Lecture Note Ser. Vol. 252, (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Alperin, R., and Wright, D., ${\rm K}_2(2, k[T, T^{-1}])$ is generated by “symbols”, Journal of Algebra 59(1): (1979), 39–46.CrossRefGoogle Scholar
Anh Tuan, B. and Ellis, G., The homology of $\mathit{{{\rm} SL}}_2(\mathbb{Z}[1/m])$ for small m, Journal of Algebra 408 (2014), 102–108.Google Scholar
Brown, K. S., Cohomology of groups. Graduate Texts in Mathematics, Vol. 87 (Springer-Verlag, New York, 1994).Google Scholar
Cohn, P. M., On the structure of the $\mathit{{{\rm} GL}}_2$ of a ring, Inst. Hautes ÉTudes Sci. Publ. Math. 30 (1966), 5–53.CrossRefGoogle Scholar
Cohn, P. M., A presentation of $\mathit{{{\rm} SL}}_2$ for Euclidean imaginary quadratic number fields, Mathematika 15(2): (1968), 156–163.CrossRefGoogle Scholar
Dennis, R. K., The ${{\rm} GE}_2$ property for discrete subrings of ${\mathbb{C}}$, Proc. American Math. Soc. 50(1): (1975), 77–82.Google Scholar
Dennis, R. K., and Stein, M. R., The functor K2: a survey of computations and problems, Lecture Notes in Math. 342 (1973), 243–280.Google Scholar
Eggleton, R. B., Lacampagne, C. B. and Selfridge, J. L., Euclidean quadratic fields, The American Mathematical Monthly 99(9): (1992), 829–837.CrossRefGoogle Scholar
Hutchinson, K., GE2-rings and a graph of unimodular rows, J. Pure Appl. Algebra 226(10): (2022), .CrossRefGoogle Scholar
Menal, P., Remarks on the $\mathit{{{\rm} GL}}_2$ of a ring, Journal of Algebra 61(2): (1979), 335–359.CrossRefGoogle Scholar
Morita, J., Chevalley groups over Dedekind domains and some problems for ${{\rm} K}_2(2,\mathbb{Z}_S)$, Toyama Math. J. 41 (2020), 83–122.Google Scholar
Nyberg-Brodda, C. -F., The abelianization of $\mathit{{\rm SL}}_2(\mathbb{Z}[\frac{1}{m}])$, Journal of Algebra, 660 (2024), .Google Scholar
Silvester, J. R., On the K2 of a free associative algebra, Proc. London Math. Soc. 26(3): (1973), 35–56.CrossRefGoogle Scholar
Stein, M. R. G., Generators, relations and coverings of Chevalley groups over commutative rings, Amer. J. Math. 93(4): (1971), 965–1004.CrossRefGoogle Scholar
Vaserstein, L. N., On the group $\mathit{{{\rm} SL}}_2$ over Dedekind rings of arithmetic type, Math. USSR Sbornik 18(2): (1972), 321–332.CrossRefGoogle Scholar
Williams, F. and Wisner, R., Cohomology of certain congruence subgroups of the modular group, Proc. Amer. Math. Soc. 126(5): (1998), 1331–1336.CrossRefGoogle Scholar