Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, William Y. C.
Dou, Donna Q. J.
and
Yang, Arthur L. B.
2013.
Brändén's Conjectures on the Boros–Moll Polynomials.
International Mathematics Research Notices,
Vol. 2013,
Issue. 20,
p.
4819.
Liu, Eric H
2017.
Skew log-concavity of the Boros-Moll sequences.
Journal of Inequalities and Applications,
Vol. 2017,
Issue. 1,
Zhu, Bao-Xuan
2018.
Positivity of Iterated Sequences of Polynomials.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 3,
p.
1993.
Chen, Herman Z.Q.
Yang, Arthur L.B.
and
Zhang, Philip B.
2018.
The real-rootedness of generalized Narayana polynomials related to the Boros-Moll polynomials.
Rocky Mountain Journal of Mathematics,
Vol. 48,
Issue. 1,
Guo, Jeremy
2022.
Higher order Turán inequalities for Boros-Moll sequences.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 8,
p.
3323.
Zhu, Bao-Xuan
2023.
On the concavity properties of certain arithmetic sequences and polynomials.
Mathematische Zeitschrift,
Vol. 305,
Issue. 3,
Zhao, James Jing Yu
2023.
A Simple Proof of Higher Order Turán Inequalities for Boros–Moll Sequences.
Results in Mathematics,
Vol. 78,
Issue. 4,
Jiang, Jungle Z.X.
and
Wang, Larry X.W.
2024.
Properties arising from Laguerre-Pólya class for the Boros-Moll numbers.
Advances in Applied Mathematics,
Vol. 154,
Issue. ,
p.
102637.
Wang, Bo
and
Zhang, Candice X. T.
2024.
Some criteria for higher order Turán inequalities in the spirit of Mařík's theorem.
Journal of Difference Equations and Applications,
Vol. 30,
Issue. 5,
p.
659.
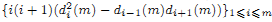 is log-concave.
is log-concave.