Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T05:31:27.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Alternative statistical methods in the study of growth and body composition of animals

Published online by Cambridge University Press:  05 November 2021

D Muldowney ,
J Connolly  and
MG Keane
D Muldowney
Affiliation:
Dept of Statistics, University College Dublin, Dublin 4, Ireland
J Connolly
Affiliation:
Dept of Statistics, University College Dublin, Dublin 4, Ireland
MG Keane
Affiliation:
Dept of Statistics, University College Dublin, Dublin 4, Ireland
Get access

Extract

Body composition of animals may change (a) in response to treatments or (b) as they grow older. Studies on (a) generally model each component of composition separately, without the constraint that predicted components sum to 1 (e.g. Keane et al 1990). Allometric regression is widely used in studies of growth and differentiation (change in component proportions). This frequently involves estimating the parameters of a linear relation 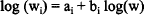between the logarithm of weight of an organ or part (Wi) and the logarithm of the weight of the whole animal (w). Sometimes the relation is between an organ and a part of the animal that contains the organ as a subcomponent. A similar difficulty as in (a) arises here also. The allometric regression equations can be recast to give predictive models for the composition of the animal at different weights. In this form the model is

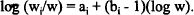
Type
Programme
Information
Proceedings of the British Society of Animal Science , Volume 1998 , 1998 , pp. 14
Copyright
Copyright © The British Society of Animal Science 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Keane, MG, More-O'Fenall, GJ, Connolly, J and Allen, P (1990) Carcass composition of serially slaughtered Friesian, Hereford x Friesian and Charolais x Friesian steers finished on two dietary energy levels. Animal Production 50:231–243.Google Scholar
Aitchison, J (1986) The statistical analysis of compositional data. Chapman and Hall.10.1007/978-94-009-4109-0CrossRefGoogle Scholar