Articles
The Equilibrium Distribution for a Clocked Buffered Switch
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 425-438
-
- Article
- Export citation
Least Busy Alternative Routing in Queueing and Loss Networks
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 439-456
-
- Article
- Export citation
An Evolution Model for Monte Carlo Estimation of Equilibrium Network Renewal Parameters
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 457-469
-
- Article
- Export citation
Output and Delay Processes in a Slotted ALOHA Multichannel Packet Radio Network with Capture
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 471-493
-
- Article
- Export citation
On the Assignment of Customers to Parallel Queues
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 495-511
-
- Article
- Export citation
On Optimal Permutation Scheduling in Stochastic Proportionate Flowshops
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 513-523
-
- Article
- Export citation
A Generalized Age-Replacement Model
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 525-541
-
- Article
- Export citation
Some Large Deviations Results in Markov Fluid Models
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 543-560
-
- Article
- Export citation
Hitting-Time Densities of a Two-Dimensional Markov Process
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 561-580
-
- Article
- Export citation
Front matter
PES volume 6 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PES volume 6 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

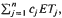 where
where 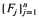 are in a class of distributions we define as SIFR, and
are in a class of distributions we define as SIFR, and 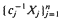 and
and 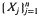 are increasing sequences of likelihood ratio-ordered and stochastic-ordered random variables, respectively, the job sequence [1, 2, …
are increasing sequences of likelihood ratio-ordered and stochastic-ordered random variables, respectively, the job sequence [1, 2, … 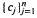 are nonincreasing, then a general cost function is minimized by the job sequence [1,2,…,
are nonincreasing, then a general cost function is minimized by the job sequence [1,2,…,