Published online by Cambridge University Press: 02 July 2021
We consider a competition involving 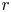 $r$ teams, where each individual game involves two teams, and where each game between teams
$r$ teams, where each individual game involves two teams, and where each game between teams 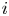 $i$ and
$i$ and 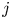 $j$ is won by
$j$ is won by 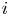 $i$ with probability
$i$ with probability 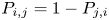 $P_{i,j} = 1 - P_{j,i}$. We suppose that
$P_{i,j} = 1 - P_{j,i}$. We suppose that 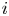 $i$ and
$i$ and 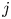 $j$ are scheduled to play
$j$ are scheduled to play 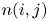 $n(i,j)$ games and say that the team that wins the most games is the winner of the competition. We show that the conditional probability that
$n(i,j)$ games and say that the team that wins the most games is the winner of the competition. We show that the conditional probability that 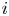 $i$ is the winner, given that
$i$ is the winner, given that 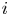 $i$ wins
$i$ wins 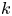 $k$ games, is increasing in
$k$ games, is increasing in 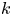 $k$. We bound the tail probability of the number of wins of the winning team. We consider the special case where
$k$. We bound the tail probability of the number of wins of the winning team. We consider the special case where 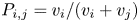 $P_{i,j} = {v_i}/{(v_i + v_j)}$, and obtain structural results on the probability that team
$P_{i,j} = {v_i}/{(v_i + v_j)}$, and obtain structural results on the probability that team 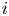 $i$ is the winner. We give efficient simulation approaches for computing the probability that team
$i$ is the winner. We give efficient simulation approaches for computing the probability that team  $i$ is the winner, and the conditional probability given the number of wins of
$i$ is the winner, and the conditional probability given the number of wins of 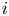 $i$.
$i$.