Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brown, Mark
2014.
VARIANCE BOUNDS UNDER A HAZARD RATE CONSTRAINT.
Probability in the Engineering and Informational Sciences,
Vol. 28,
Issue. 2,
p.
203.
Daly, Fraser
2016.
Compound geometric approximation under a failure rate constraint.
Journal of Applied Probability,
Vol. 53,
Issue. 3,
p.
700.


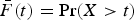 . An application to birth and death processes is discussed.
. An application to birth and death processes is discussed.