Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T07:38:29.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-Statically Cooled Markov Chains

Published online by Cambridge University Press:  27 July 2009

Madhav Desai ,
Sunil Kumar  and
P. R. Kumar
Madhav Desai
Affiliation:
Digital Equipment Corporation Boston, Massachusetts 01749
Sunil Kumar
Affiliation:
Department of Electrical and Computer Engineering and the Coordinated Science Laboratory, University of Illinois, 1308 West Main Street, Urbana, Illinois 61801
P. R. Kumar
Affiliation:
Department of Electrical and Computer Engineering and the Coordinated Science Laboratory, University of Illinois, 1308 West Main Street, Urbana, Illinois 61801
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider time-inhomogeneous Markov chains on a finite state-space, whose transition probabilitiespij(t) = cijε(t)Vij are proportional to powers of a vanishing small parameter ε(t). We determine the precise relationship between this chain and the corresponding time-homogeneous chains pij= cijε(t)vij, as ε ↘ 0. Let {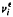} be the steady-state distribution of this time-homogeneous chain. We characterize the orders {ηι} in 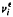= θ(εηι). We show that if ε(t) ↘ 0 slowly enough, then the timewise occupation measures βι := sup { q > 0 | Prob(x(t) = i) = + ∞}, called the recurrence orders, satisfy βi — βj = ηj — ηi. Moreover, : = { ηι|ηι = minj} is the set of ground states of the time-homogeneous chain, then x(t) → . in an appropriate sense, whenever η(t) is “cooled” slowly. We also show that there exists a critical ρ* such that x(t) → if and only if 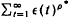= + ∞. 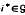We characterize this critical rate as ρ* = max.min min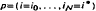 max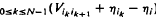. Finally, we provide a graph algorithm for determining the orders [ηi] [βi] and the critical rate ρ*.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 8 , Issue 1 , January 1994 , pp. 1 - 19
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anantharam, V. & Tsoucas, P. (1989). A proof of the Markov chain tree theorem. Statistics and Probability Letters 8: 189–192.CrossRefGoogle Scholar
2.Anily, S. & Federgruen, A. (1987). Simulated annealing methods with general acceptance probabilities. Journal of Applied Probability 24: 657–667.CrossRefGoogle Scholar
3.Chiang, T.S. & Chow, Y. (1989). On the asymptotic behavior of some inhomogeneous Markov processes. Annals of Probability 17: 1483–1502.Google Scholar
4.Connors, D.P. (1988). Balance of recurrence order in time-inhomogeneous Markov chains with application to simulated annealing. Ph.D. thesis, University of Illinois, Urbana, IL.Google Scholar
5.Connors, D.P. & Kumar, P.R. (1988). Balance of recurrence order in time-inhomogeneous Markov chains with application to simulated annealing. Probability in the Engineering and Informational Sciences 2: 157–184.CrossRefGoogle Scholar
6.Connors, D.P. & Kumar, P.R. (1989). Simulated annealing type Markov chains and their order balance equations. SIAM Journal on Control and Optimization 27: 1440–1462.CrossRefGoogle Scholar
7.Friedlin, M.I. & Wentzell, A.D. (1984). Random perturbations of dynamical systems. New York: Springer-Verlag.CrossRefGoogle Scholar
8.Geman, S. & Geman, D. (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence PAMI-6: 721–741.CrossRefGoogle ScholarPubMed
9.Hajek, B. (1988). Cooling schedules for optimal annealing. Mathematics of Operations Research 13: 311–329.CrossRefGoogle Scholar
10.Hill, T.L. (1966). Studies in irreversible thermodynamics IV. Diagrammatic representation of steady state fluxes for unimolecular systems. Journal of Theoretical Biology 10: 442–459.CrossRefGoogle ScholarPubMed
11.Kirkpatrick, S., Gelatt, C.D., & Vecchi, M.P. (1983). Optimization by simulated annealing. Science 220: 671–680.CrossRefGoogle ScholarPubMed
12.Kohler, H.H. & Vollmerhaus, E. (1980). The frequency of cyclic processes in biological multi-state systems. Journal of Mathematical Biology 9: 275–290.CrossRefGoogle Scholar
13.Leighton, F.T. & Rivest, R.L. (1983). The Markov chain tree theorem. Computer Science Technical Report MIT/LCS/TM-249, MIT, Cambridge, MA.Google Scholar
14.Leighton, F.T. & Rivest, R.L. (1986). Estimating a probability using finite memory. IEEE Transactions on information Theory IT-32(6): 733–742.CrossRefGoogle Scholar
15.Mitra, D., Romeo, F., & Sangiovanni-Vincentelli, A. (1986). Convergence and finite-tme behavior of simulated annealing. Advances in Applied Probability 18: 747–771.CrossRefGoogle Scholar
16.Shubert, B.O. (1975). A flow-graph formula for the stationary distribution of a Markov chain. IEEE Transactions on Systems, Man and Cybernetics SMC-5: 565–566.CrossRefGoogle Scholar
17.Tsitsiklis, J.N. (1989). Markov chains with rare transitions and simulated annealing. Mathematics of Operations Research 14: 70–90.CrossRefGoogle Scholar