Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T20:54:35.423Z Has data issue: false hasContentIssue false
  • English
  • Français

PRESERVATION OF LOG-CONCAVITY AND LOG-CONVEXITY UNDER OPERATORS

Published online by Cambridge University Press:  14 February 2020

Wanwan Xia ,
Tiantian Mao  and
Taizhong Hu Open the ORCID record for Taizhong Hu [Opens in a new window]
Wanwan Xia
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, Anhui 230026, China; School of Physical and Mathematical Sciences, Nanjing Tech University, Nanjing, Jiangsu 211816, China E-mail: [email protected]
Tiantian Mao
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, Anhui 230026, China E-mail: [email protected]; [email protected]
Taizhong Hu
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, Anhui 230026, China E-mail: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Log-concavity [log-convexity] and their various properties play an increasingly important role in probability, statistics, operations research and other fields. In this paper, we first establish general preservation theorems of log-concavity and log-convexity under operator 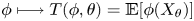$\phi \longmapsto T(\phi , \theta )=\mathbb {E}[\phi (X_\theta )]$, θ ∈ Θ, where Θ is an interval of real numbers or an interval of integers, and the random variable 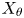$X_\theta$ has a distribution function belonging to the family 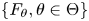$\{F_\theta , \theta \in \Theta \}$ possessing the semi-group property. The proofs are based on the theory of stochastic comparisons and weighted distributions. The main results are applied to some special operators, for example, operators occurring in reliability, Bernstein-type operators and Beta-type operators. Several known results in the literature are recovered.

Keywords

bernstein-type operatorbeta-type operatorgamma processpoisson processreliability propertiesrenewal processsemi-group propertystochastic orderweighted distribution
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 35 , Issue 3 , July 2021 , pp. 451 - 464
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adell, J.A., Badía, F.G., & de la Cal, J. (1993). Beta-type operators preserve shape properties. Stochastic Processes and Their Applications 48: 1–8.CrossRefGoogle Scholar
2.An, M.Y. (1998). Log-concavity versus log-convexity: a complete characterization. Journal of Economic Theory 80: 350–369.CrossRefGoogle Scholar
3.Badía, F.G. (2009). On the preservation of log convexity and log concavity under some classical Bernstein-type operators. Journal of Mathematical Analysis and Applications 360: 485–490.CrossRefGoogle Scholar
4.Badía, F.G. & Sangüesa, C. (2008). Preservation of reliability classes under mixtures of renewal processes. Probability in the Engineering and Informational Sciences 22: 1–17.CrossRefGoogle Scholar
5.Badía, F.G. & Sangüesa, C. (2014). Log-concavity for Bernstein-type operators using stochastic orders. Journal of Mathematical Analysis and Applications 413: 953–962.CrossRefGoogle Scholar
6.Badía, F.G. & Sangüesa, C. (2015). Inventory models with nonlinear shortage costs and stochastic lead times: applications of shape properties of randomly stopped counting processes. Naval Research Logistics 62: 345–356.CrossRefGoogle Scholar
7.Bagnoli, M. & Bergstrom, T. (2005). Log-concave probability and its applications. Economic Theory 26: 445–469.CrossRefGoogle Scholar
8.Barlow, R.E. & Proschan, F. (1981). Statistical theory of reliability and life testing. Silver Spring, MD: To Begin With.Google Scholar
9.Bobkov, S. & Madiman, M. (2011). Concentration of the information in data with log-concave distributions. Annals of Probability 39: 1528–1543.CrossRefGoogle Scholar
10.Borell, C. (1973). Complements of Lyapunov's inequality. Mathematische Annalen 205: 323–331.CrossRefGoogle Scholar
11.Capéraá, P. (1988). Tail ordering and asymptotic efficiency of rank tests. Annals of Statistics 3: 1045–1069.Google Scholar
12.de la Cal, J. & Cárcamo, J. (2003). On uniform approximation by some classical Bernstein-type operators. Journal of Mathematical Analysis and Applications 279: 625–638.CrossRefGoogle Scholar
13.de la Cal, J. & Cárcamo, J. (2007). On the approximation of convex functions by Bernstein-type operators. Journal of Mathematical Analysis and Applications 334: 1106–1115.CrossRefGoogle Scholar
14.Dharmadhikari, S. & Joag-dev, K (1988). Unimodality, convexity and applications. New York: Academic Press.Google Scholar
15.Finner, H. & Roters, M. (1993). Distribution functions and log-concavity. Communications in Statistics: Theory and Methods 22: 2381–2396.CrossRefGoogle Scholar
16.Finner, H. & Roters, M. (1997). Log-concavity and inequalities for chi-square, F and Beta distributions with applications in multiple comparisons. Statistica Sinica 7: 771–787.Google Scholar
17.Hu, T. & Zhuang, W. (2006). Stochastic comparisons of m-spacings. Journal of Statistical Planning and Inference 136: 33–42.CrossRefGoogle Scholar
18.Joag-dev, K., Kochar, S., & Proschan, F. (1995). A general composition theorem and its applications to certain partial orderings of distributions. Statistics and Probability Letters 22: 111–119.CrossRefGoogle Scholar
19.Kahn, J. & Neiman, M. (2010). Negative correlation and log-concavity. Random Structures and Algorithms 37: 271–406.CrossRefGoogle Scholar
20.Li, Y., Yu, L., & Hu, T. (2012). Probability inequalities for weighted distributions. Journal of Statistical Planning and Inference 142: 1272–1278.CrossRefGoogle Scholar
21.Liggett, T.M. (1997). Ultra log-concave sequence and negative dependence. Journal of Combinatorial Theory, Series A 79: 315–325.CrossRefGoogle Scholar
22.Marshall, A.W., Olkin, I., & Arnold, B.C. (2011). Inequalities: theory of majorization and its applications, 2nd ed. New York: Springer.Google Scholar
23.Marsiglietti, A. & Kostina, V. (2018). A lower bound on the differential entropy of log-concave random vectors with applications. Entropy 115: article number 185, 24 pages.Google Scholar
24.Misra, N. & van der Meulen, E.C. (2003). On stochastic properties of m-spacings. Journal of Statistical Planning and Inference 115: 683–697.CrossRefGoogle Scholar
25.Mu, X. (2015). Log-concavity of a mixture of beta distributions. Statistics and Probability Letters 99: 125–130.CrossRefGoogle Scholar
26.Patil, G.P. & Rao, C.R. (2002). The weighted distributions: a survey and their applications. In Krishnaiah, P.R. (ed.), Applications of statistic. Amsterdam: North-Holland, pp. 385–405.Google Scholar
27.Patil, G.P. (2002). Weighted distributions. In El-Shaarawi, A.H. & Piegorsch, W.W. (eds), Encyclopedia of Environmetrics, vol. 4. Chichester: John Wiley & Sons, Ltd., pp. 2369–2377.Google Scholar
28.Proschan, F. & Sethuraman, J. (1977). Schur functions in statistics I. The preservation theorem. Annals of Statistics 5: 256–262.CrossRefGoogle Scholar
29.Ross, S.M., Shanthikumar, J.G., & Zhu, Z. (2005). On increasing-failure-rate random variables. Journal of Applied Probability 42: 797–809.CrossRefGoogle Scholar
30.Saumard, A. & Wellner, J.A. (2014). Log-concavity and strong log-concavity: a review. Statistics Surveys 8: 45–114.CrossRefGoogle ScholarPubMed
31.Sengupta, D. & Nanda, A.K. (1999). Log-concave and concave distributions in reliability. Naval Research Logistics 46: 419–433.3.0.CO;2-B>CrossRefGoogle Scholar
32.Shaked, M. & Shanthikumar, J.G (2007). Stochastic orders. New York: Springer.CrossRefGoogle Scholar
33.Shanthikumar, J.G. (1985). Bilateral phase-type distributions. Naval Research Logistics Quarterly 32: 119–136.CrossRefGoogle Scholar
34.Wang, Y. & Yeh, Y.-N. (2007). Log-concavity and LC-positivity. Journal of Combinatorial Theory, Series A 114: 195–210.CrossRefGoogle Scholar
35.Yu, Y. (2010). Relative log-concavity and a pair of triangle inequalities. Bernoulli 16: 459–470.CrossRefGoogle Scholar