No CrossRef data available.
Article contents
On stochastic ordering among extreme shock models
Published online by Cambridge University Press: 28 October 2022
Abstract
In the usual shock models, the shocks arrive from a single source. Bozbulut and Eryilmaz [(2020). Generalized extreme shock models and their applications. Communications in Statistics – Simulation and Computation 49(1): 110–120] introduced two types of extreme shock models when the shocks arrive from one of 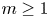 $m\geq 1$ possible sources. In Model 1, the shocks arrive from different sources over time. In Model 2, initially, the shocks randomly come from one of
$m\geq 1$ possible sources. In Model 1, the shocks arrive from different sources over time. In Model 2, initially, the shocks randomly come from one of 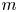 $m$ sources, and shocks continue to arrive from the same source. In this paper, we prove that the lifetime of Model 1 is less than Model 2 in the usual stochastic ordering. We further show that if the inter-arrival times of shocks have increasing failure rate distributions, then the usual stochastic ordering can be generalized to the hazard rate ordering. We study the stochastic behavior of the lifetime of Model 2 with respect to the severity of shocks using the notion of majorization. We apply the new stochastic ordering results to show that the age replacement policy under Model 1 is more costly than Model 2.
$m$ sources, and shocks continue to arrive from the same source. In this paper, we prove that the lifetime of Model 1 is less than Model 2 in the usual stochastic ordering. We further show that if the inter-arrival times of shocks have increasing failure rate distributions, then the usual stochastic ordering can be generalized to the hazard rate ordering. We study the stochastic behavior of the lifetime of Model 2 with respect to the severity of shocks using the notion of majorization. We apply the new stochastic ordering results to show that the age replacement policy under Model 1 is more costly than Model 2.
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 37 , Issue 4 , October 2023 , pp. 961 - 972
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press


