Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Comtet, Alain
and
Majumdar, Satya N
2005.
Precise asymptotics for a random walker’s maximum.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2005,
Issue. 06,
p.
P06013.
Majumdar, Satya N.
Comtet, Alain
and
Ziff, Robert M.
2006.
Unified Solution of the Expected Maximum of a Discrete Time Random Walk and the Discrete Flux to a Spherical Trap.
Journal of Statistical Physics,
Vol. 122,
Issue. 5,
p.
833.
Ziff, Robert M
Majumdar, Satya N
and
Comtet, Alain
2007.
General flux to a trap in one and three dimensions.
Journal of Physics: Condensed Matter,
Vol. 19,
Issue. 6,
p.
065102.
Palacios, José Luis
2008.
On the Simple Symmetric Random Walk and its Maximal Function.
The American Statistician,
Vol. 62,
Issue. 2,
p.
138.
Galbraith, Steven
and
Ruprai, Raminder S.
2009.
Cryptography and Coding.
Vol. 5921,
Issue. ,
p.
368.
Ziff, Robert M.
Majumdar, Satya N.
and
Comtet, Alain
2009.
Capture of particles undergoing discrete random walks.
The Journal of Chemical Physics,
Vol. 130,
Issue. 20,
Krapivsky, P L
Majumdar, Satya N
and
Rosso, Alberto
2010.
Maximum ofNindependent Brownian walkers till the first exit from the half-space.
Journal of Physics A: Mathematical and Theoretical,
Vol. 43,
Issue. 31,
p.
315001.
Withers, Christopher S.
and
Nadarajah, Saralees
2010.
METHODS FOR SYMMETRIZING RANDOM VARIABLES.
Probability in the Engineering and Informational Sciences,
Vol. 24,
Issue. 4,
p.
549.
Majumdar, Satya N.
Comtet, Alain
and
Randon-Furling, Julien
2010.
Random Convex Hulls and Extreme Value Statistics.
Journal of Statistical Physics,
Vol. 138,
Issue. 6,
p.
955.
Galbraith, Steven D.
and
Ruprai, Raminder S.
2010.
Public Key Cryptography – PKC 2010.
Vol. 6056,
Issue. ,
p.
368.
Majumdar, Satya N.
2010.
Universal first-passage properties of discrete-time random walks and Lévy flights on a line: Statistics of the global maximum and records.
Physica A: Statistical Mechanics and its Applications,
Vol. 389,
Issue. 20,
p.
4299.
Wergen, Gregor
Majumdar, Satya N.
and
Schehr, Grégory
2012.
Record statistics for multiple random walks.
Physical Review E,
Vol. 86,
Issue. 1,
Dekker, Anthony H.
and
Taylor, Richard
2013.
Synchronization Properties of Trees in the Kuramoto Model.
SIAM Journal on Applied Dynamical Systems,
Vol. 12,
Issue. 2,
p.
596.
Ben-Naim, E
and
Krapivsky, P L
2014.
Persistence of random walk records.
Journal of Physics A: Mathematical and Theoretical,
Vol. 47,
Issue. 25,
p.
255002.
Krivan, William
2016.
The Elusive Quest for Preserved Quantities in Financial Time Series: Making a Case for Intraday Trading Strategies.
SSRN Electronic Journal,
Mounaix, Philippe
and
Schehr, Grégory
2017.
First gap statistics of long random walks with bounded jumps.
Journal of Physics A: Mathematical and Theoretical,
Vol. 50,
Issue. 18,
p.
185001.
Grebenkov, Denis S
Lanoiselée, Yann
and
Majumdar, Satya N
2017.
Mean perimeter and mean area of the convex hull over planar random walks.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2017,
Issue. 10,
p.
103203.
Majumdar, Satya N
Mounaix, Philippe
and
Schehr, Grégory
2017.
Survival probability of random walks and Lévy flights on a semi-infinite line.
Journal of Physics A: Mathematical and Theoretical,
Vol. 50,
Issue. 46,
p.
465002.
Mounaix, Philippe
Majumdar, Satya N
and
Schehr, Grégory
2018.
Asymptotics for the expected maximum of random walks and Lévy flights with a constant drift.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2018,
Issue. 8,
p.
083201.
Hartich, David
and
Godec, Aljaž
2019.
Extreme value statistics of ergodic Markov processes from first passage times in the large deviation limit.
Journal of Physics A: Mathematical and Theoretical,
Vol. 52,
Issue. 24,
p.
244001.
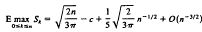 ,
,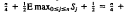 O(n½), when the rectangle sides are 2n independent uniform random draws from [0,1].
O(n½), when the rectangle sides are 2n independent uniform random draws from [0,1].

