Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T08:04:19.007Z Has data issue: false hasContentIssue false
  • English
  • Français

A LOSS SYSTEM WITH SKILL-BASED SERVERS UNDER ASSIGN TO LONGEST IDLE SERVER POLICY

Published online by Cambridge University Press:  08 June 2012

Ivo Adan  and
Gideon Weiss
Ivo Adan
Affiliation:
Department of Mechanical Engineering, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands E-mail: [email protected]
Gideon Weiss
Affiliation:
Department of Statistics, The University of Haifa, Mount Carmel 31905, Israel E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

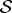We consider a memoryless loss system with servers = {1, …, J}, and with customer types 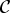= {1, …, I}. Servers are multi-type: server j works at rate μj, and can serve a subset of customer types C(j). An arriving customer will go to the longest idling server which can serve him, or be lost. We obtain a simple explicit steady-state distribution for this system, and calculate various performance measures of this system in steady state. We provide some illustrative examples. We compare this system with a similar system discussed recently by Adan, Hurkens, and Weiss [1]. We also show that this system is insensitive, the results hold also for general service time distributions.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 26 , Issue 3 , July 2012 , pp. 307 - 321
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adan, I.J.B.F., Hurkens, C., & Weiss, G. (2010). A reversible Erlang loss system with multitype customers and multitype servers. Probability in Engineering and Informational Sciences 24: 535–548.CrossRefGoogle Scholar
2.Adan, I.J.B.F. & Weiss, G. (2011). Exact FCFS matching rates for two infinite multi-type sequences. Operations Research to appear.Google Scholar
3.Busic, A., Gupta, V., & Mairesse, J. (2010). Stability of the bipartite matching model, Preprint, arxiv:1003.3477v1 [cs.DM].Google Scholar
4.Caldentey, R., Kaplan, E.H., & Weiss, G., (2009). FCFS infinite bipartite matching of servers and customers. Advances in Applied Probability 41: 695–730.CrossRefGoogle Scholar
5.Sevastyanov, B.A. (1957). An ergodic theorem for Markov processes and its application to telephone systems with refusals Theory of Probability and its Applications 2: 104–112.CrossRefGoogle Scholar
6.Talreja, R. & Whitt, W. (2008). Fluid models for overloaded multi-class many-service queueing systems with FCFS routing. Management Science 54: 1513–1527.CrossRefGoogle Scholar
7.Visschers, J.W.C.H., Adan, I.J.B.F., & Weiss, G. (2011). A product form solution to a system with multi-type customers and multi-type servers. Queueing Systems 70: 269–298.CrossRefGoogle Scholar