Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T16:44:38.604Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPANSIONS FOR MOMENTS OF COMPOUND POISSON DISTRIBUTIONS

Published online by Cambridge University Press:  28 March 2013

S. Nadarajah ,
C.S. Withers  and
S.A.A. Bakar
S. Nadarajah
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK E-mail: [email protected]
C.S. Withers
Affiliation:
Applied Mathematics Group, Industrial Research Limited, Lower Hutt, New Zealand E-mail: [email protected]
S.A.A. Bakar
Affiliation:
Institute of Mathematical Sciences, University of Malaya, 50603 Kuala Lumpur, Malaysia E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Expansions for moments of 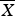$\overline{X}$, the mean of a random sample of size n, are given for both the univariate and multivariate cases. The coefficients of these expansions are simply Bell polynomials. An application is given for the compound Poisson variable SN, where 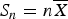$S_{n} = n \overline{X}$ and N is a Poisson random variable independent of X1, X2, …, yielding expansions that are computationally more efficient than the Panjer recursion formula and Grubbström and Tang's formula.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 27 , Issue 3 , July 2013 , pp. 319 - 331
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abramowitz, M. & Stegun, I.A. (1964). Handbook of mathematical functions. Washington, DC: US Department of Commerce, National Bureau of Standards, Applied Mathematics Series, vol. 55.Google Scholar
2.Avramidis, A.N. & Matzinger, H. (2002). Convergence of the stochastic mesh estimator for pricing American options. In Proceedings of the 2002 Winter Simulation Conference, Yücesan, E., Chen, C.-H., Snowdon, J.L., & Charnes, J.M. (eds.), pp. 1560–1567.CrossRefGoogle Scholar
3.Coën, A., Racicot, F.E., & Théoret, R. (2009). Higher moments as risk instruments to discard errors in variables: the case of the Fama and French model. Journal of Global Business Administration 1: 2–22.Google Scholar
4.Comtet, L. (1974). Advanced combinatorics. Dordrecht: Reidel.CrossRefGoogle Scholar
5.Embrechts, P. & Frei, M. (2009). Panjer recursion versus FFT for compound distributions. Mathematical Methods of Operations Research 69: 497–508.CrossRefGoogle Scholar
6.Grubbström, R.W. & Tang, O. (2006). The moments and central moments of a compound distribution. European Journal of Operational Research 170: 106–119.CrossRefGoogle Scholar
7.Kendall, M.G. & Stuart, A. (1969). The advanced theory of statistics, vol. 1, 3rd ed.London: Griffin.Google Scholar
8.Panjer, H.H. (1981). Recursive evaluation of a family of compound distributions. ASTIN Bulletin 12: 22–26.CrossRefGoogle Scholar
9.Panjer, H.H. & Willmot, G.E. (1992). Insurance risk models Schaumburg: Society of Actuaries.Google Scholar
10.Sundt, B. & Vernic, R. (2009). Recursions for convolutions and compound distributions with insurance applications. Heidelberg: Springer Verlag.Google Scholar
11.Taleb, N. (1997). Dynamic hedging. New York: John Wiley and Sons.Google Scholar
12.Tchouproff, A.A. (1918). On the mathematical expectation of the moments of frequency distribution. Biometrika 12: 140–169.CrossRefGoogle Scholar