Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T09:02:53.846Z Has data issue: false hasContentIssue false
  • English
  • Français

DRAWING MULTISETS OF BALLS FROM TENABLE BALANCED LINEAR URNS

Published online by Cambridge University Press:  28 March 2013

Hosam M. Mahmoud
Hosam M. Mahmoud*
Affiliation:
The George Washington University, Washington, D.C. 20052, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the evolution of an urn of balls of two colors, where one chooses a pair of balls and observes rules of ball addition according to the outcome. A nonsquare ball addition matrix of the form 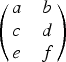$\left( \matrix{a & b \cr c & d \cr e & f}\right)$ corresponds to such a scheme, in contrast to pólya urn models that possess a square ball addition matrix. We look into the case of constant row sum (the so-called balanced urns) and identify a linear case therein. Two cases arise in linear urns: the nondegenerate and the degenerate. Via martingales, in the nondegenerate case one gets an asymptotic normal distribution for the number of balls of any color. In the degenerate case, a simpler probability structure underlies the process. We mention in passing a heuristic for the average-case analysis for the general case of constant row sum.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 27 , Issue 2 , April 2013 , pp. 147 - 162
Copyright
Copyright © Cambridge University Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Athreya, K. & Karlin, S. (1968). Embedding of urn schemes into continuous time Markov branching process and related limit theorems. Annals of Mathematical Statistics 39: 1801–1817.CrossRefGoogle Scholar
2.Athreya, K. & Ney, P. (1972). Branching Processes. New York: Springer-Verlag.CrossRefGoogle Scholar
3.Bagchi, A. & Pal, A. (1985). Asymptotic normality in the generalized Pólya-Eggenberger urn model with applications to computer data structures. SIAM Journal on Algebraic and Discrete Methods 6: 394–405.CrossRefGoogle Scholar
4.Bai, Z. & Hu, F. (1999). Asymptotic theorems for urn models with non-homogeneous generating matrices. Stochastic Processes and Their Applications 80: 87–101.CrossRefGoogle Scholar
5.Balaji, S. & Mahmoud, H. (2006). Exact and Limiting distributions in diagonal Pólya processes. The Annals of the Institute of Statistical Mathematics 58: 171–185.CrossRefGoogle Scholar
6.Balaji, S., Mahmoud, H., & Watanabe, O. (2006). Distributions in the Ehrenfest process. Statistics and Probability Letters 76: 666–674.CrossRefGoogle Scholar
7.Bernstein, S. (1940). Sur un problème du schéma des urnes à composition variable. Comptes Rendus (Doklady) de l’ Academic des Sciences de l’ URSS 28: 5–7.Google Scholar
8.Chen, M. & Wei, C. (2005). A new urn model. Journal of Applied Probability 42: 964–976.CrossRefGoogle Scholar
9.Eggenberger, F. & Pólya, G. (1923). Über die statistik verketetter vorgäge. Zeitschrift für Angewandte Mathematik und Mechanik 1: 279–289.CrossRefGoogle Scholar
10.Flajolet, P., Dumas, P., & Puyhaubert, V. (2006). Some exactly solvable models of urn process theory. In Philippe Chassaing AG, (Ed) Discrete Mathematics and Computer Science Proceedings, 59–118.CrossRefGoogle Scholar
11.Flajolet, P., Gabarró, J., & Pekari, H. (2005). Analytic urns. The Annals of Probability 33: 1200–1233.CrossRefGoogle Scholar
12.Freedman, D. (1965). Bernard Friedman's urn. Annals of Mathematical Statistics 36: 956–970.CrossRefGoogle Scholar
13.Friedman, B. (1949). A simple urn model. Communications of Pure and Applied Mathematics 2: 59–70.CrossRefGoogle Scholar
14.Gouet, R. (1989). A martingale approach to strong convergence in a generalized Pólya-Eggenberger urn model. Statistics and Probability Letters 8: 225–228.CrossRefGoogle Scholar
15.Gouet, R. (1993). Martingale functional central limit theorems for a generalized Pólya Urn. Annals of Probability 21: 1624–1639.CrossRefGoogle Scholar
16.Hall, P. & Heyde, C. (1980). Martingale limit theory and its applications. New York: Academic Press.Google Scholar
17.Janson, S. (2004). Functional limit theorems for multitype branching processes and generalized Pólya urns. Stochastic Processes and Applications 110: 177–245.CrossRefGoogle Scholar
18.Janson, S. (2005). Asymptotic degree distribution in random recursive trees. Random Structures and Algorithms 26: 69–83.CrossRefGoogle Scholar
19.Johnson, N. & Kotz, S. (1977). Urn Models and their applications. New York: Wiley.Google Scholar
20.Johnson, N., Kotz, S., & Mahmoud, H. (2004). Pólya-type urn models with multiple drawings. Journal of the Iranian Statistical Society 3: 165–173.Google Scholar
21.Kotz, S. & Balakrishnan, N. (1997). Advances in urn models during the past two decades. In Balakrishman, N. (ed.), Advances in combinatorial methods and applications to probability and statistics, vol 49, Boston: Birkhäuser, pp. 203–257.CrossRefGoogle Scholar
22.Kotz, S., Mahmoud, H., & Robert, P. (2000). On generalized pólya urn models. Statistics and Probability Letters 49: 163–173.CrossRefGoogle Scholar
23.Mahmoud, H. (1998). On rotations in fringe-balanced binary trees. Information Processing Letters 65: 41–46.CrossRefGoogle Scholar
24.Mahmoud, H. (2003). Pólya urn models and connections to random trees: A review. Journal of the Iranian Statistical Society 2: 53–114.Google Scholar
25.Mahmoud, H. & Smythe, R. (1992). Asymptotic joint normality of outdegrees of nodes in random recursive trees. Random Structures and Algorithms 3: 255–266.CrossRefGoogle Scholar
26.Mahmoud, H. & Smythe, R. (1995). Probabilistic analysis of bucket recursive trees. Theoretical Computer Science 144: 221–249.CrossRefGoogle Scholar
27.Mahmoud, H., Smythe, R., & Szymański, J. (1993). On the structure of plane-oriented recursive trees and their branches. Random Structures and Algorithms 4: 151–176.CrossRefGoogle Scholar
28.Mahmoud, H. & Tsukiji, T. (2000). A limit law for outputs in random recursive circuits. Algorithmica 31: 403–412.Google Scholar
29.Pemantle, R. (1990). Nonconvergence to unstable points in urn models and stochastic approximations. Annals of Probability 18: 698–712.CrossRefGoogle Scholar
30.Pemantle, R. (2007). A survey of random processes with reinforcement. Probability Surveys 4: 1–79.CrossRefGoogle Scholar
31.Rosenblatt, A. (1940). Sur le concept de contagion de M. G. Pólya dans le calcul des probabilités. Proc. Acad. Nac. Cien. Exactas, Fis. Nat., Peru (Lima), 3: 186–204.Google Scholar
32.Savkevich, V. (1940). Sur le schéma des urnes à composition variable. Comptes Rendus (Doklady) de l’ Academic des Sciences de l’ URSS 28: 8–12.Google Scholar
33.Smythe, R. (1996). Central limit theorems for urn models. Stochastic Processes and Their Applications 65: 115–137.CrossRefGoogle Scholar