Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T21:43:39.408Z Has data issue: false hasContentIssue false
  • English
  • Français

A Coupling Proof of the Asymptotic Normality of the Permutation Oscillation

Published online by Cambridge University Press:  27 July 2009

John E. Angus
John E. Angus
Affiliation:
Department of Mathematics, The Claremont Graduate School, Claremont, California 91711
Get access Rights & Permissions [Opens in a new window]

Abstract

For each n ≥ 1, let Πn = (π1, π2, …, πn) be a random permutation of the integers 1,2, …, n. The quantity Bn = Σ 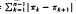measures the degree of oscillation of Πn and is an important measure in the study of sorting algorithms. In this work the asymptotic normality of Bn is derived under the assumption that, for each n ≥ 1, Πn is uniformly distributed over the n! permutations of 1,2, …, n. The proof relies on coupling (π1, π2, …, πn) with a sequence of independent and identically distributed U(0,1) random variables and offers a more probabilistic and computationally simpler alternative to the method of moments proof of Chao, Bai, and Liang (1993, Probability in the Engineering and Informational Sciences 7: 227–235).

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 9 , Issue 4 , October 1995 , pp. 615 - 621
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Billingsley, P. (1968). Convergence of probability measures. New York: John Wiley.Google Scholar
2.Billingsley, P. (1986). Probability and measure, 2nd ed.New York: John Wiley.Google Scholar
3.Chao, C., Bai, Z., & Liang, W. (1993). Asymptotic normality for oscillation of permutation. Probability in the Engineering and Informational Sciences 7: 227–235.CrossRefGoogle Scholar
4.Chung, K.L. (1976). A course in probability theory, 2nd ed.New York: Academic Press.Google Scholar
5.Diaconis, P. & Graham, R. (1977). Spearman's footrule as a measure of disarray. Journal of the Royal Statistical Society B 39: 262–268.Google Scholar
6.Hajek, J. (1961). Some extensions of the Wold-Wolfowitz-Noether theorem. Annals of Mathematical Statistics 32: 506–523.CrossRefGoogle Scholar
7.Hoeffding, W. (1951). A combinatorial central limit theorem. Annals of Mathematical Statistics 22: 558–566.CrossRefGoogle Scholar