Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T15:16:14.854Z Has data issue: false hasContentIssue false
  • English
  • Français

Chi-Square Goodness of Fit: A Failure Rate Perspective

Published online by Cambridge University Press:  27 July 2009

Mark Brown  and
Marcia H. Flicker
Mark Brown
Affiliation:
Department of Mathematics The City College, CUNY New York, New York 10031
Marcia H. Flicker
Affiliation:
Graduate School of Business Administration Fordham University Bronx, New York 10458
Get access Rights & Permissions [Opens in a new window]

Abstract

Employing a failure rate approach, we propose a test statistic, 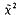, for the classic goodness-of-fit problem. It is then shown that a variation of 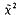, obtained by replacing observed variances by expected variances (an unwise change in our point of view), leads to the classical test statistic, x2. We argue that 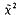should be better approximated by a chi-square distribution, and thus employing 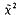, the true p−values should be closer to the nominal p−values than under x2 Various other comparisons of the two tests are made.

Type
Articles
Information
Probability in the Engineering and Informational Sciences , Volume 5 , Issue 3 , July 1991 , pp. 273 - 284
Copyright
Copyright © Cambridge University Press 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Birnbaum, A. (1962). On the foundations of statistical inference. Journal of the American Stansf ical Association 57: 269–326.CrossRefGoogle Scholar
Cox, D.R. (1972). Regression models and life tables. Journal of the Royal Statistics Society B, 34: 187–220.Google Scholar
Hyde, J. (1977). Testing survival under right censoring and left truncation. Biometrika 64: 225–230.CrossRefGoogle Scholar
Lehmann, E.L. (1959). Testing statistical hypotheses. New York: John Wiley & Sons.Google Scholar
Mantel, N. (1963). Chi-square tests with one degree of freedom: Extensions of the Mantel– Haenszel procedure. Journal of the American Statistical Association 58: 690–700.Google Scholar
Mantel, H. (1966). Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemotherapy Reports 50: 163–170.Google ScholarPubMed