1 Introduction
Social actors rarely act independent of other’s influences. Legislators confer before important votes (Kingdon Reference Kingdon1973; Matthews and Stimson Reference Matthews and Stimson1975) and seek one another’s cosponsorships on legislation (Kirkland and Gross Reference Kirkland and Gross2014); international firms form networks of production locations in many different countries (Echandi, Krajcovicova, and Qiang Reference Echandi, Krajcovicova and Qiang2015); countries are embedded within dense networks of trade, intergovernmental organizations (IGOs), and alliances (Maoz Reference Maoz2010; Hays, Schilling, and Boehmke Reference Hays, Schilling and Boehmke2015; Chyzh Reference Chyzh2016; Gallop Reference Gallop2016). Growing theoretical attention to the study of interdependence has, in turn, created a demand for more appropriate methodological tools that directly model such interdependence—a demand that spurred burgeoning statistical research in spatial/network analysis (Franzese, Hays, and Kachi Reference Franzese, Hays and Kachi2012; Gile and Handcock Reference Gile and Handcock2015; Minhas, Hoff, and Ward Reference Minhas, Hoff and Ward2016).
This paper builds on this research by focusing on modeling of what we refer to as localized network processes—a class of theoretical processes involving the formation of network structures as a function of other structures that form within the network. If we think of actors as nodes within the network, and pairwise relationships among them as edges, then in the simplest form localized network processes would include the formation of network edges as a function of other edges within the network. The location affects these types of action–reaction processes: where within the network an action occurs affects the likelihood of reaction to it. Localized network processes include the formation of coalitions and voting blocs, balancing and bandwagoning, policy learning, imitation, diffusion, tipping-point dynamics, and cascade effects.
Central theories behind coalition formation, for example, emphasize that alignments within coalitions (edges) happen in response to formation of alignments (edges) within a rival coalition. Voting blocs in legislatures form to balance opposing blocs or bandwagon as one coalition rushes to provide support to their co-partisans. Thus, if we think of legislators as nodes within a network, and an act of cosponsoring a piece of legislation as a formation of an edge between the sponsor and the cosponsor, then the relational processes of interest may involve bandwagoning—additional cosponsorships by other ideationally similar legislators—or balancing—an introduction of a competing bill cosponsored by legislators from the opposite part of the ideological spectrum. Analogously, alliances among countries frequently form with the goal of balancing against an alliance of a political rival: for example, the Soviet bloc formed the Warsaw Pact in response to the United States and its allies forming the North Atlantic Treaty Organization (NATO) in the aftermath of World War II.
Baccini and Dür (Reference Baccini and Dür2012) posit a similar theoretical process behind the formation of preferential trade agreements, arguing that pairs of countries sign mainly as a response to the preferential trade agreements formed by other countries, with which they are competing for exports. Political parties frequently form coalitions, or join together to share manifestos and ballot lines. Lobby groups have been shown to form in response to other special-interests forming lobbies of their own (Gray and Lowery Reference Gray and Lowery2001).
Such substantively important processes, however, have not yet been modeled using the traditional network approaches, such as exponential random graph models (ERGMs) or latent variable models (LVMs). ERGMs are focused on global or system-level rather than localized network configurations.Footnote 1 The resulting inferences related to the global structure of the network (i.e., the probability of occurrence of particular structures within the network) do not easily lend themselves to local-level insights (i.e., where in the network are these structures most likely to be observed) (Casleton, Nordman, and Kaiser Reference Casleton, Nordman and Kaiser2017). LVMs allow for testing for the presence of localized edge dependencies, yet not for their direct modeling.Footnote 2
We propose a unified theoretical and statistical framework for explicit theoretical modeling of localized network processes using the tools offered by the spatial statistics literature on Markov random fields, in particular, a local structure graph model (LSGM). Our approach relies on more careful theorizing regarding what constitutes a node and/or an edge within a network. We argue that the decision to treat particular network features as nodes and edges must be tailored to the specific empirical application. Thus, while in traditional approaches actors are treated as network nodes and relationships among them as edges, modeling localized network processes may require, for example, treating edges (e.g., alliances) as network nodes, and connectivities among edges (e.g., belonging to the same neighborhood) as second-degree edges.
The proposed theoretical framework emphasizes connectivities among edges, or second-degree connectivities, in a general sense. The source of connectivity may stem from discrete edge characteristics (e.g., two edges are connected if they share a common node or if they connect two similar nodes) or may be measured on a continuous scale (e.g., intensity/strength of connections among edges depends on a continuous dyad-of-edges-level attribute).
We use a Monte Carlo simulations experiment to demonstrate that the model allows for practical estimation of parameters that are easily interpretable. We briefly compare the performance of LSGM to that of a spatial probit, an alternative spatial estimator for binary dependent variables.Footnote 3 Finally, we supplement simulations with two empirical applications: the formation of the alliance network among countries between 1946–2007 and the formation of the network of legislative cosponsorships on labor-related legislation in the Senate of the 107th US Congress.
2 Modeling Localized Network Processes
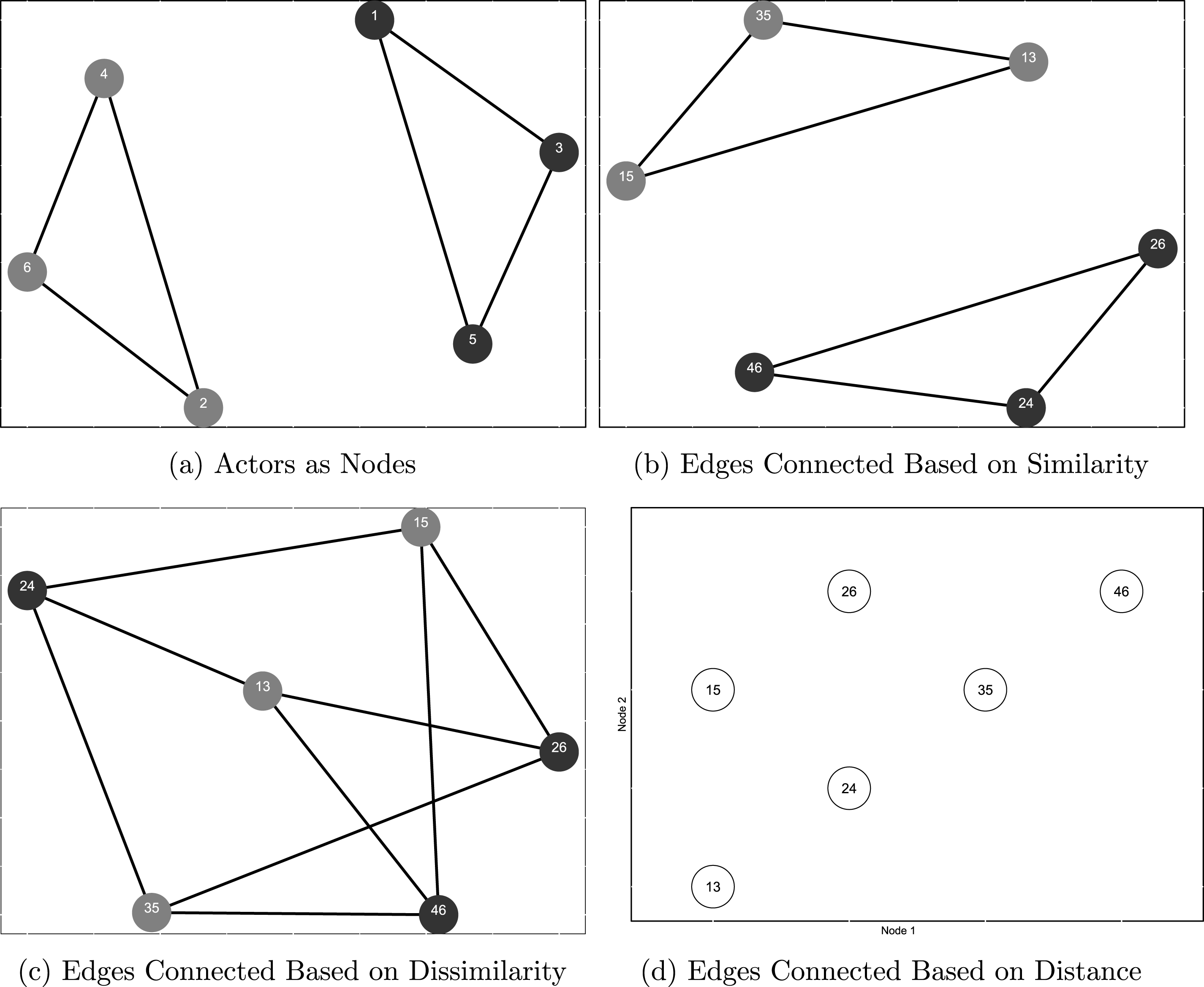
Figure 1. Alternative conceptualizations of nodes and edges.
From the theoretical perspective, the key to our approach is that any network project starts with the important decision of which features of the data are treated as nodes and edges—a decision that is determinative of the analysis and any inferences that will follow. Traditional network-based studies of legislative cooperation, for example, tend to take a nodes-as-actors approach, that is, treat individual legislators as nodes that are connected by edges if they engage in some form of cooperation (e.g., cosponsor a piece of legislation). A theoretical alternative to the nodes-as-actors approach is what we refer to as the nodes-as-actions approach—a model that treats acts of cooperation as nodes which are connected/related based on some source of dependence (e.g., two cosponsorships are related if they occur among members of the same party).
To illustrate, suppose we start with a network shown in Figure 1a—a network that consists of six nodes (e.g., legislators), some of which are connected by edges (e.g., cosponsored a piece of legislation). Figure 1b shows a reconceptualization of the same network as a “flipped” network, in which each edge from Figure 1a is now depicted as a node, and relationships between each pair of edges (whether they connect two nodes of the same color) as edges. For example, node 24 in Figure 1b corresponds to the edge between nodes 2 and 4 in Figure 1a, and nodes 13 and 35 are connected by an edge because they both connect nodes of the same color in Figure 1a. Thus, the features of the network that were treated as nodes in the original network (Figure 1a) became edges in the flipped network in Figure 1b, with the focus shifting from dependence among actors to that among actions.
The decision to adopt one or the other approach is paramount, as it delineates the scope/limits of the study’s theoretical/empirical inferences. The nodes-as-actors approach limits the scope to actor- or dyadic-level inferences (e.g., cooperation is more likely to happen between legislators of the same party). In contrast, the nodes-as-actions approach allows for zeroing in on possible dependence processes among acts of legislative cooperation: for example, cosponsorships follow a tipping-point process with each act of cosponsorship by a member of one party increasing the probability of another cosponsorship by a member of the same party.
Returning to Figure 1, if we think of color/parity as representing party identification, then a network visualized in Figure 1b allows us to model cosponsorships as a tipping point or a bandwagoning process: initial introduction triggers a cascade of cosponsorships among legislators from the same party. Figure 1c that connects cosponsorships of different colors, would allow for studying an alternative process, in which growing cooperation among members of one party may trigger an increase in cooperation within the opposing party. Connections among nodes in the flipped network may also be continuous, that is, in Figure 1d edges are placed in a two-dimensional space with
![]() $x$
- and
$x$
- and
![]() $y$
- coordinates corresponding to the numerical identifiers of the nodes that make up each edge. In the latter example, the strength of connections among edges is measured using the Euclidean distance, that is, edges 13 and 24 are separated by a shorter Euclidean distance and, therefore, have a stronger connection than edges 13 and 46.
$y$
- coordinates corresponding to the numerical identifiers of the nodes that make up each edge. In the latter example, the strength of connections among edges is measured using the Euclidean distance, that is, edges 13 and 24 are separated by a shorter Euclidean distance and, therefore, have a stronger connection than edges 13 and 46.
In more general terms, the nodes-as-actions approach provides a theoretical tool for studying localized network processes, in which specific dyads affect other specific dyads or—in network parlance—processes, in which network edges realize (or not) in response to other edges. As we show in the rest of the paper, such processes may be modeled within the statistical framework of Markov random fields (MRF) models (Kaiser and Caragea Reference Kaiser and Caragea2009) or their econometrics alternative—spatial autoregression (SAR) and its variants (e.g., spatial probit). We provide an in-depth comparison between these two estimation approaches, including a Monte Carlo experiment, to argue that the MRF framework is more straightforward in both interpretability of results as wells as the assumptions regarding the underlying theoretical process in Section 4.
3 Statistical Estimation of Local Structures within Networks
In this section, we demonstrate a statistical approach to modeling localized network outcomes—a local structure graph model (LSGM)—using the framework of the Markov random field models (Kaiser and Caragea Reference Kaiser and Caragea2009). The formulation of an LSGM is derived from the spatial statistics literature (Besag Reference Besag1974, Reference Besag1975).
In short, the formulation of an LSGM starts with specifying a set of full conditional distributions for each potential edge in the network, that is, the distribution of the presence/absence of an edge given the outcomes for all potential edges and a set of exogenous covariates. Thus, each conditional distribution is specified in terms of a neighborhood/spatial connectivity structure (denote it as matrix W) that explicitly identifies the degree of “local” dependency between all pairs of (potential) edges within the network. If we think of a joint sponsorship of a legislation as a formation of a network edge, then the connectivity/dependence between each pair of potential cosponsorships may stem from party identification, ideological distance, etc. The connectivity matrix of interest is then used in the specification of the conditional distribution of each edge’s realization as a function of realizations of every other edge, such that edge pairs with greater dependence exert greater effect on each other’s realizations than pairs of edges with weaker dependence (Besag Reference Besag1974; Hays, Kachi, and Franzese Reference Hays, Kachi and Franzese2010; Anselin Reference Anselin2013).Footnote 4
More formally, suppose
![]() $i$
is a potential edge in a network of
$i$
is a potential edge in a network of
![]() $n$
edges (e.g., a cosponsorship in the example discussed above),
$n$
edges (e.g., a cosponsorship in the example discussed above),
![]() $i\in \{1,2,\ldots ,n\}$
, so that
$i\in \{1,2,\ldots ,n\}$
, so that
![]() $i$
’s location is denoted as
$i$
’s location is denoted as
![]() $s_{i}=(u_{i},v_{i})$
in Cartesian space. Next, define
$s_{i}=(u_{i},v_{i})$
in Cartesian space. Next, define
![]() $i$
’s neighbors as
$i$
’s neighbors as
![]() $N_{i}$
, so that
$N_{i}$
, so that
![]() $\mathbf{y}(N_{i})$
is a vector of outcomes in
$\mathbf{y}(N_{i})$
is a vector of outcomes in
![]() $i$
’s neighbors and
$i$
’s neighbors and
![]() $\mathbf{y}(N_{i})=\{\mathbf{y}(s_{j}):s_{j}\in N_{i}\}$
. If dependencies among edges are binary, then the next step is to make a Markov assumption of conditional spatial independence of the form:
$\mathbf{y}(N_{i})=\{\mathbf{y}(s_{j}):s_{j}\in N_{i}\}$
. If dependencies among edges are binary, then the next step is to make a Markov assumption of conditional spatial independence of the form:
Thus, in the case of binary dependencies among edges, the realization of any given edge
![]() $i$
is dependent on realization of every other edge to which it is connected (i.e., an outcome in
$i$
is dependent on realization of every other edge to which it is connected (i.e., an outcome in
![]() $i$
is affected by the outcomes in all edges from the neighborhood
$i$
is affected by the outcomes in all edges from the neighborhood
![]() $N_{i}$
), yet conditionally independent of the realization of edges in its neighbors’ neighborhoods. Intuitively, this assumption simply means that
$N_{i}$
), yet conditionally independent of the realization of edges in its neighbors’ neighborhoods. Intuitively, this assumption simply means that
![]() $i$
is affected by its immediate neighbors rather than by its neighbors’ neighborhoods.
$i$
is affected by its immediate neighbors rather than by its neighbors’ neighborhoods.
Note that, if dependencies among edges are measures on a continuous scale, as is the case of interest here, we can simply define
![]() $i$
’s neighbors as
$i$
’s neighbors as
![]() $-i$
, so that
$-i$
, so that
![]() $\mathbf{y}_{-i}=\mathbf{y}(s_{-i})=\{\mathbf{y}(s_{j}):s_{j}\neq s_{i}\}$
. In case of continuous dependencies, the Markov assumption (1) is redundant.
$\mathbf{y}_{-i}=\mathbf{y}(s_{-i})=\{\mathbf{y}(s_{j}):s_{j}\neq s_{i}\}$
. In case of continuous dependencies, the Markov assumption (1) is redundant.
Further, denote the binary random variable,
![]() $y(s_{i})=y_{i}$
, that records the presence or absence of an edge, such that:
$y(s_{i})=y_{i}$
, that records the presence or absence of an edge, such that:
Next, we must specify the neighborhood structure or the connectivity matrix whose entries correspond to the presence/strength of dependence among (potential) edges. Edges may belong to a set of discrete (nonoverlapping) neighborhoods or a single neighborhood with a continuous measure of the strength of dependence (i.e., some edges are located in closer proximity than others). More formally, we can say that an edge
![]() $i$
is conditionally independent of edge
$i$
is conditionally independent of edge
![]() $j$
unless
$j$
unless
![]() $j$
is a neighbor of
$j$
is a neighbor of
![]() $i$
(and hence
$i$
(and hence
![]() $i$
is a neighbor of
$i$
is a neighbor of
![]() $j$
). Of course, if connectivity among edges is measured on a continuous scale, then the realization of edge
$j$
). Of course, if connectivity among edges is measured on a continuous scale, then the realization of edge
![]() $i$
is dependent on realizations of all other edges (every edge is in every other edge’s neighborhood). A neighborhood is measured via an
$i$
is dependent on realizations of all other edges (every edge is in every other edge’s neighborhood). A neighborhood is measured via an
![]() $n$
-by-
$n$
-by-
![]() $n$
matrix W, whose
$n$
matrix W, whose
![]() $ij$
cell is a binary or a continuous measure of connectivity between edges
$ij$
cell is a binary or a continuous measure of connectivity between edges
![]() $i$
and
$i$
and
![]() $j$
and with 0s on the major diagonal (edges have no connectivity with themselves). In political science applications, the connectivity matrix W may represent physical or geographical distance between edges, their ideological similarity, or any other pairwise measures of relationship.
$j$
and with 0s on the major diagonal (edges have no connectivity with themselves). In political science applications, the connectivity matrix W may represent physical or geographical distance between edges, their ideological similarity, or any other pairwise measures of relationship.
Consistent with the legislative example above, we assume a binary conditional distribution, which is expressed in exponential family form as:
where
![]() $A_{i}$
is a natural parameter function and
$A_{i}$
is a natural parameter function and
![]() $B_{i}=\log [1+\exp (A_{i}(\mathbf{y}(N_{i})))]$
. Conditional dependencies among edges are modeled through the natural parameter function as:
$B_{i}=\log [1+\exp (A_{i}(\mathbf{y}(N_{i})))]$
. Conditional dependencies among edges are modeled through the natural parameter function as:
where
![]() $\log (\frac{\unicode[STIX]{x1D705}_{i}}{1-\unicode[STIX]{x1D705}_{i}})=\mathbf{x}_{i}^{T}\boldsymbol{\unicode[STIX]{x1D6FD}}$
,
$\log (\frac{\unicode[STIX]{x1D705}_{i}}{1-\unicode[STIX]{x1D705}_{i}})=\mathbf{x}_{i}^{T}\boldsymbol{\unicode[STIX]{x1D6FD}}$
,
![]() $\mathbf{x}_{i}$
is a vector of exogenous covariates,
$\mathbf{x}_{i}$
is a vector of exogenous covariates,
![]() $\boldsymbol{\unicode[STIX]{x1D6FD}}$
is a vector of estimation parameters,
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
is a vector of estimation parameters,
![]() $w_{ij}$
is the
$w_{ij}$
is the
![]() $ij^{th}$
element of a matrix of connectivities among edges, W,
$ij^{th}$
element of a matrix of connectivities among edges, W,
![]() $\unicode[STIX]{x1D702}$
is a dependence parameter, and
$\unicode[STIX]{x1D702}$
is a dependence parameter, and
![]() $y_{j}$
is the outcome in location
$y_{j}$
is the outcome in location
![]() $s_{j}$
. Parameters
$s_{j}$
. Parameters
![]() $\boldsymbol{\unicode[STIX]{x1D6FD}}$
are associated with the global effects of the exogenous covariates, while
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
are associated with the global effects of the exogenous covariates, while
![]() $\unicode[STIX]{x1D702}$
is the estimate of the local dependence among observations, with positive values indicating a direct relationship between edge realizations in neighboring units and negative values indicating an inverse relationship. Notably, the above parameterization of the natural parameter function involves centering by global parameters
$\unicode[STIX]{x1D702}$
is the estimate of the local dependence among observations, with positive values indicating a direct relationship between edge realizations in neighboring units and negative values indicating an inverse relationship. Notably, the above parameterization of the natural parameter function involves centering by global parameters
![]() $\unicode[STIX]{x1D705}_{j}$
, which has been shown to enhance interpretation of the estimates by separating global and local effects (Kaiser, Caragea, and Furukawa Reference Kaiser, Caragea and Furukawa2012).
$\unicode[STIX]{x1D705}_{j}$
, which has been shown to enhance interpretation of the estimates by separating global and local effects (Kaiser, Caragea, and Furukawa Reference Kaiser, Caragea and Furukawa2012).
The formulation of the (spatial) dependence term,
![]() $\unicode[STIX]{x1D702}\sum _{j=1}^{n}w_{ij}(y_{j}-\unicode[STIX]{x1D705}_{j})$
, ensures that it can make a positive or a negative contribution to the natural parameter function. This term increases the value of the natural parameter function if the realization of the neighbors’ values exceeds its expectation,
$\unicode[STIX]{x1D702}\sum _{j=1}^{n}w_{ij}(y_{j}-\unicode[STIX]{x1D705}_{j})$
, ensures that it can make a positive or a negative contribution to the natural parameter function. This term increases the value of the natural parameter function if the realization of the neighbors’ values exceeds its expectation,
![]() $y_{j}>\unicode[STIX]{x1D705}_{j}$
, and decreases its value if the observed value is less than the expected value,
$y_{j}>\unicode[STIX]{x1D705}_{j}$
, and decreases its value if the observed value is less than the expected value,
![]() $y_{j}<\unicode[STIX]{x1D705}_{j}$
. Since in the binary case
$y_{j}<\unicode[STIX]{x1D705}_{j}$
. Since in the binary case
![]() $y_{j}\in \{0,1\}$
and
$y_{j}\in \{0,1\}$
and
![]() $0<\unicode[STIX]{x1D705}_{j}<1$
, a positive dependence parameter,
$0<\unicode[STIX]{x1D705}_{j}<1$
, a positive dependence parameter,
![]() $\unicode[STIX]{x1D702}>0$
, indicates that an absence of edges in neighboring locations,
$\unicode[STIX]{x1D702}>0$
, indicates that an absence of edges in neighboring locations,
![]() $y_{j}=0$
, has a negative effect on the probability that
$y_{j}=0$
, has a negative effect on the probability that
![]() $y_{i}=1$
, and the presence of edges in neighboring locations,
$y_{i}=1$
, and the presence of edges in neighboring locations,
![]() $y_{j}=1$
, has a positive effect. Analogously, a negative dependence parameter,
$y_{j}=1$
, has a positive effect. Analogously, a negative dependence parameter,
![]() $\unicode[STIX]{x1D702}<0$
, implies the opposite: the absence of edges in neighboring locations,
$\unicode[STIX]{x1D702}<0$
, implies the opposite: the absence of edges in neighboring locations,
![]() $y_{j}=0$
, has a positive effect on the probability of edge realizations in
$y_{j}=0$
, has a positive effect on the probability of edge realizations in
![]() $y_{i}$
, and the presence of edges in neighboring locations,
$y_{i}$
, and the presence of edges in neighboring locations,
![]() $y_{j}=1$
, has a negative effect.
$y_{j}=1$
, has a negative effect.
If the connectivity among nodes, W, is measured on a continuous scale, s.t. larger values of
![]() $w_{ij}$
denote larger differences between
$w_{ij}$
denote larger differences between
![]() $i$
and
$i$
and
![]() $j$
, then a positive dependence parameter,
$j$
, then a positive dependence parameter,
![]() $\unicode[STIX]{x1D702}>0$
, indicates that a presence of an edge in a distant location
$\unicode[STIX]{x1D702}>0$
, indicates that a presence of an edge in a distant location
![]() $y_{j}=1$
has a positive effect on the probability of edge realizations in
$y_{j}=1$
has a positive effect on the probability of edge realizations in
![]() $y_{i}$
, which is consistent with the logic of balancing. A negative dependence parameter,
$y_{i}$
, which is consistent with the logic of balancing. A negative dependence parameter,
![]() $\unicode[STIX]{x1D702}<0$
, in contrast, would indicate that a presence of an edge in a distant location has a negative effect on the probability of
$\unicode[STIX]{x1D702}<0$
, in contrast, would indicate that a presence of an edge in a distant location has a negative effect on the probability of
![]() $y_{i}=1$
, which is consistent with such processes as clustering or bandwagoning.
$y_{i}=1$
, which is consistent with such processes as clustering or bandwagoning.
LSGM’s formulation, therefore, results in a relatively straightforward interpretation of dependence parameters: for fixed values of exogenous variables and other model parameters, the dependence parameter in an LSGM is directly proportional to the log odds ratio of the presence of an edge, relative to an independence (or Erdos–Renyi) model. Thus, a doubling of
![]() $\unicode[STIX]{x1D702}$
represents a doubling of this log odds ratio (see expression 3.6 in Caragea and Kaiser Reference Caragea and Kaiser2009).Footnote
5
$\unicode[STIX]{x1D702}$
represents a doubling of this log odds ratio (see expression 3.6 in Caragea and Kaiser Reference Caragea and Kaiser2009).Footnote
5
As is the case for the general class of Markov random field models, of which the above model is a special case, the specification of a full conditional distribution leads to a valid joint distribution under certain conditions. For the LSGM in Equation 2, one of these conditions is that the connectivity matrix
![]() $\text{}\text{W}$
be symmetric for all pairs of edges, that is,
$\text{}\text{W}$
be symmetric for all pairs of edges, that is,
![]() $w_{ij}=w_{ji}$
.Footnote
6
This symmetry condition, of course, implies that, in contrast to the typical specification of SAR models, the connectivity matrix must not be row standardized, as row standardizing will violate this assumption.Footnote
7
Model parameters may be obtained by maximizing a log pseudolikelihood (PL), which is a summation of the log of the conditional distributions (Besag Reference Besag1975):
$w_{ij}=w_{ji}$
.Footnote
6
This symmetry condition, of course, implies that, in contrast to the typical specification of SAR models, the connectivity matrix must not be row standardized, as row standardizing will violate this assumption.Footnote
7
Model parameters may be obtained by maximizing a log pseudolikelihood (PL), which is a summation of the log of the conditional distributions (Besag Reference Besag1975):
where
The point estimates recovered by maximizing the PL function have been shown to be consistent for the general case of MRF models (Guyon Reference Guyon1995). Standard errors may be obtained via parametric bootstrap. In what follows, we use a Monte Carlo simulations experiment to demonstrate the properties of the parameter estimates for the special case of the model presented in Equation 2, and follow up with two empirical applications to data on international alliances and legislative cosponsorships.
Unlike the SAR model, LSGM is easily generalized to other distributions within the exponential family by simply re-specifying the natural parameter function. Thus, the above example could be re-formulated to model continuous, multinomial, ordered, or count data. In this respect, LSGM, and MRF models more broadly,Footnote 8 also present a more direct and general modeling approach that does not require assumptions related to latent variable distributions, as is the case with SAR models.
4 A Monte Carlo Comparison: LSGM vs. Spatial Probit
To further showcase LSGM properties, we perform a Monte Carlo experiment, in which we generate a set of 500 independent networks, according to the LSGM data-generating process, estimate an LSGM and a spatial probit (SP)—an alternative estimator for modeling spatial dependence in binary data—and discuss the results. Replication files for this analysis are available from the Political Analysis Dataverse (Chyzh and Kaiser Reference Chyzh and Kaiser2018).
Although both LSGM and SP allow for modeling dependence in binary data, the two estimators are based on rather different theoretical assumptions regarding the nature of the modeled dependence, and are not substitutable in any general sense. SP was developed within the spatial econometrics literature to model spatially dependent outcomes as steady-state equilibria resulting from some shock that reverberates through the whole system (Beron, Murdoch, and Vijverberg Reference Beron, Murdoch and Vijverberg2003; Franzese, Hays, and Cook Reference Franzese, Hays and Cook2016). The effect of the shock is conditioned by the weights matrix. An example of an outcome that would follow such a process is the spread of an economic crisis: that is, a currency collapse in one country affects all of its economic partners, as well as all the partners of their partner’s partners, and so on, both directly, and indirectly (e.g., countries may affect each other through their mutual economic partners). The spatial parameter then represents the first-order, or the instantaneous effect of dependence, whereas the total or the cumulative effect may be calculated by specifying the number of partners/neighbors, their outcomes, and the connectivity matrix.Footnote 9 A possible weakness of the SP estimator is that any measurement bias may multiply through the system via direct and indirect connectivities (see the Appendix for a Monte Carlo example).
In contrast, in an LSGM model, the dependence structure is limited to only first-order effects: an outcome is affected by the neighbors’ outcomes, but not indirectly affected by the neighbors’ neighbors’ outcomes. That is, all of the spatial effects are assumed to work through first-order connectivities: while state A’s rival B may have formed an alliance in response to that formed by their rival C, A’s probability of forming an alliance is only affected by B and not by C. Moreover, while SP treats spatial dependence as conditioned only by the weights matrix, the specification of an LSGM includes global parameter centering, which places greater weights on “less expected” outcomes in neighboring units (the expectation is determined as a function of the exogenously specified covariates). Relating this back to the alliance example, the Soviet Union’s alliance with Nazi Germany (an unexpected alliance among United States’ adversaries) affects the United States’ probability of seeking additional allies more than a Soviet alliance with Serbia (which is unsurprising). The final distinction between LSGM and SP is a matter of mathematical/theoretical elegance: unlike SP, which models the binary outcome via a latent variable approach, LSGM estimators model the binary outcome directly as an odds ratio of the probability that an outcome is realized and its complement.
4.1 Monte Carlo Set-up
While the choice of the estimator must be theoretically driven, our Monte Carlo example highlights the practical differences in resulting estimates. We start by generating information for
![]() $N=100$
observations (edges) with characteristics captured by variable
$N=100$
observations (edges) with characteristics captured by variable
![]() $X_{i}$
, drawn from a standard normal distribution. We proceed to convert these data to a dyadic format (pairs of edges), by pairing each observation with each other observation and omitting self-referencing pairs of the type
$X_{i}$
, drawn from a standard normal distribution. We proceed to convert these data to a dyadic format (pairs of edges), by pairing each observation with each other observation and omitting self-referencing pairs of the type
![]() $i-i$
for a total of
$i-i$
for a total of
![]() $n=9,900$
edges. To generate a meaningful connectivity matrix among edges, W, we place each pair on an evenly spaced ten-by-ten grid and calculate the Euclidean distance between the two units making up each edge. We treat
$n=9,900$
edges. To generate a meaningful connectivity matrix among edges, W, we place each pair on an evenly spaced ten-by-ten grid and calculate the Euclidean distance between the two units making up each edge. We treat
![]() $X_{i}$
and W as the fixed part of the simulation.
$X_{i}$
and W as the fixed part of the simulation.
The task of generating the random variable,
![]() $Y(s_{i})$
, is achieved via a Gibbs sampler procedure in accordance with the following steps. We start with a randomly initialized network (Erdos–Renyi network) of starting values, in which each pair of the 100 observations is related with a probability 0.5. We then use
$Y(s_{i})$
, is achieved via a Gibbs sampler procedure in accordance with the following steps. We start with a randomly initialized network (Erdos–Renyi network) of starting values, in which each pair of the 100 observations is related with a probability 0.5. We then use
![]() $X_{i}$
, W, and the fixed values of the parameters (
$X_{i}$
, W, and the fixed values of the parameters (
![]() $\unicode[STIX]{x1D6FD}_{0}=1$
,
$\unicode[STIX]{x1D6FD}_{0}=1$
,
![]() $\unicode[STIX]{x1D6FD}_{1}=1$
, and
$\unicode[STIX]{x1D6FD}_{1}=1$
, and
![]() $\unicode[STIX]{x1D702}=0.05$
) to update this initial network one observation at a time (each observation as a function of the network so far), according to the LSGM process (Equations 3 and 4), until we obtain a complete new network. This new network is then fed back into the sampler as the new set of initial values, and the same process is followed to generate a third complete network, and so on.
$\unicode[STIX]{x1D702}=0.05$
) to update this initial network one observation at a time (each observation as a function of the network so far), according to the LSGM process (Equations 3 and 4), until we obtain a complete new network. This new network is then fed back into the sampler as the new set of initial values, and the same process is followed to generate a third complete network, and so on.
We repeat the above steps until we obtain a total 252,000 complete networks. Since according to this process, each network is generated as a function of the previous network (and the very first network is randomly initialized), the norm is to discard some number of the resulting networks for burnin and then proceed to retain every
![]() $k$
th network after that (k is referred to as thinning). The rationale is that, while iterative updating of the initial network allows to create spatial dependence, burnin and thinning help “break” between-network dependence, so that we can treat the networks that remain after burnin and thinning as independent of each other. After experimenting with different values for burnin and thinning, we chose to discard the first 2,000 of the 252,000 networks and retain every 500th network of the subsequent networks. As a result, we are left with 500 complete independent networks.
$k$
th network after that (k is referred to as thinning). The rationale is that, while iterative updating of the initial network allows to create spatial dependence, burnin and thinning help “break” between-network dependence, so that we can treat the networks that remain after burnin and thinning as independent of each other. After experimenting with different values for burnin and thinning, we chose to discard the first 2,000 of the 252,000 networks and retain every 500th network of the subsequent networks. As a result, we are left with 500 complete independent networks.
We then estimated an LSGM and two versions of SP—one with a row-standardized W and one with an unstandardized W—on each of these 500 networks. LSGM was estimated using the pseudolikelihood presented in Equation 4. The SP model was estimated using the procedure outlined in Beron, Murdoch, and Vijverberg (Reference Beron, Murdoch and Vijverberg2003), with the model specified as:
where
![]() $\mathbf{Wy}^{\ast }$
is the spatial lag,
$\mathbf{Wy}^{\ast }$
is the spatial lag,
![]() $\mathbf{W}$
is the spatial connectivity matrix, with element
$\mathbf{W}$
is the spatial connectivity matrix, with element
![]() $w_{ij}$
giving the connectivity between units
$w_{ij}$
giving the connectivity between units
![]() $i$
and
$i$
and
![]() $j$
;
$j$
;
![]() $\unicode[STIX]{x1D702}$
is the estimation parameter of the strength of spatial interdependence among units; matrix
$\unicode[STIX]{x1D702}$
is the estimation parameter of the strength of spatial interdependence among units; matrix
![]() $\mathbf{X}$
contains values of the exogenous covariates; and
$\mathbf{X}$
contains values of the exogenous covariates; and
![]() $\boldsymbol{\unicode[STIX]{x1D6FD}}$
is the vector of estimated coefficients on each of these covariates. Consistent with the theory behind probit estimation, the latent variable
$\boldsymbol{\unicode[STIX]{x1D6FD}}$
is the vector of estimated coefficients on each of these covariates. Consistent with the theory behind probit estimation, the latent variable
![]() $\mathbf{y}^{\ast }$
maps to the observed binary outcome,
$\mathbf{y}^{\ast }$
maps to the observed binary outcome,
![]() $\mathbf{y}$
, such that
$\mathbf{y}$
, such that
![]() $y_{i}=1$
if
$y_{i}=1$
if
![]() $y_{i}^{\ast }>0$
, and
$y_{i}^{\ast }>0$
, and
![]() $y_{i}=0$
otherwise.
$y_{i}=0$
otherwise.
The results are presented in Figure 2. Thick curves represent kernel density graphs of the LSGM estimates for each parameter, thin curves represent SP estimates with a row-standardized W, and thick dashed lines represent SP with an unstandardized W. As expected, the estimates of LSGM converge around the true values of each parameter. The positive coefficient
![]() $\unicode[STIX]{x1D702}$
indicates the presence of inverse dependence among the realizations of neighboring edges, that is, the probability of an edge in location
$\unicode[STIX]{x1D702}$
indicates the presence of inverse dependence among the realizations of neighboring edges, that is, the probability of an edge in location
![]() $s_{i}$
decreases with realizations of edges in
$s_{i}$
decreases with realizations of edges in
![]() $i$
’s neighbors. LSGM’s standard errors on
$i$
’s neighbors. LSGM’s standard errors on
![]() $\unicode[STIX]{x1D6FD}_{1}$
and
$\unicode[STIX]{x1D6FD}_{1}$
and
![]() $\unicode[STIX]{x1D702}$
are small relative to the coefficients, which indicates the efficiency of the model for the theoretically relevant variables. The standard error on the intercept
$\unicode[STIX]{x1D702}$
are small relative to the coefficients, which indicates the efficiency of the model for the theoretically relevant variables. The standard error on the intercept
![]() $\unicode[STIX]{x1D6FD}_{0}$
, however, is rather large, which may limit the model’s predictive power.
$\unicode[STIX]{x1D6FD}_{0}$
, however, is rather large, which may limit the model’s predictive power.
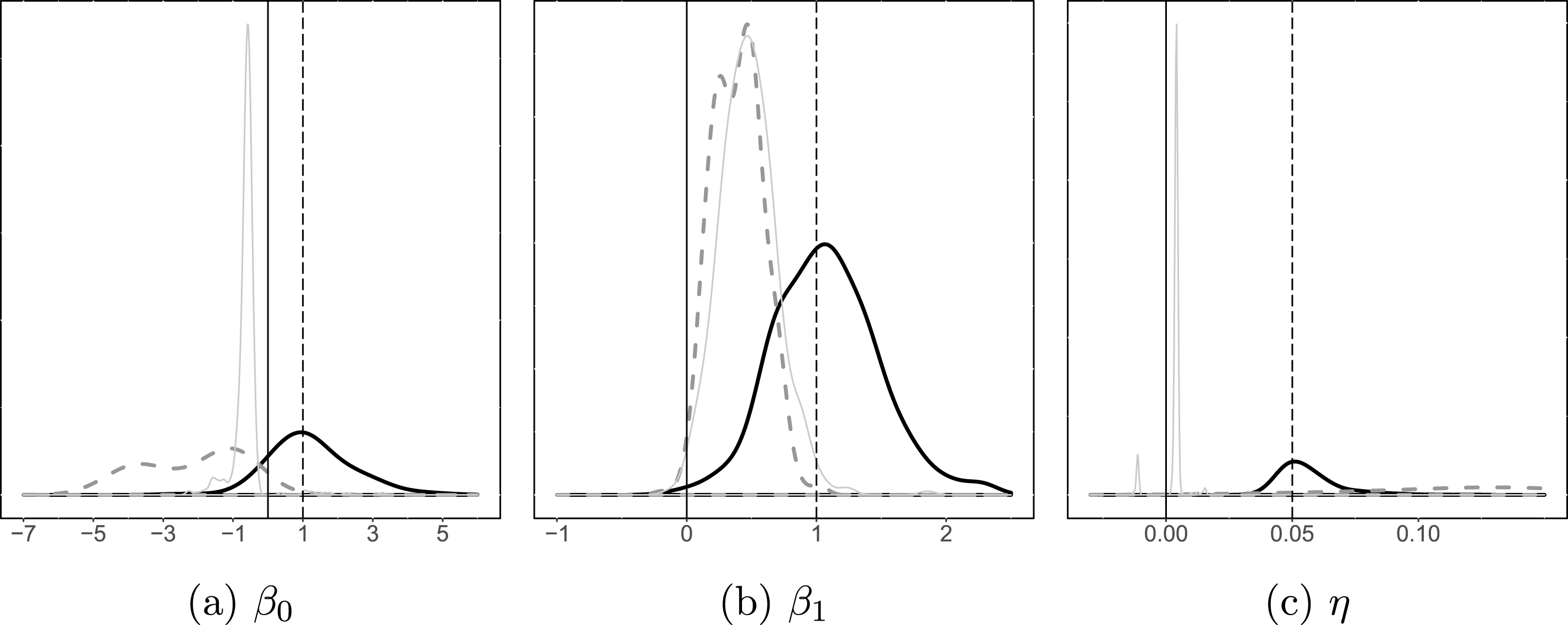
Figure 2. Monte Carlo results for parameter estimates. Notes: Dashed vertical lines represent the true values of the parameters. Thick curves represent kernel density graphs of the LSGM estimates, thin curves represent SP with a row-standardized W, and thick dashed lines represent SP with an unstandardized W. Results were estimated on 500 simulated networks with 2,000 burnin and 500 for thinning.
The caveat of comparing LSGM estimates to those of SP is that the two are based on different distributional assumptions—logit for LSGM vs probit for SP. Probit estimates are generally somewhat larger than the corresponding logit estimates. Recall also that while LSGM’s dependence coefficient
![]() $\unicode[STIX]{x1D702}$
is directly interpretable (e.g., as long as the connectivity matrix
$\unicode[STIX]{x1D702}$
is directly interpretable (e.g., as long as the connectivity matrix
![]() $\mathbf{W}$
is specified such that larger values denote stronger dependence, a positive coefficient indicates presence of positive dependence) (Caragea and Kaiser Reference Caragea and Kaiser2009), the same is not necessarily true for the SP dependence coefficient, which represents the instantaneous (prefeedback) effects of spatial dependence (e.g., Cressie Reference Cressie1993; Franzese and Hays Reference Franzese and Hays2007, 406). Even acknowledging these caveats, one can see that SP estimates of
$\mathbf{W}$
is specified such that larger values denote stronger dependence, a positive coefficient indicates presence of positive dependence) (Caragea and Kaiser Reference Caragea and Kaiser2009), the same is not necessarily true for the SP dependence coefficient, which represents the instantaneous (prefeedback) effects of spatial dependence (e.g., Cressie Reference Cressie1993; Franzese and Hays Reference Franzese and Hays2007, 406). Even acknowledging these caveats, one can see that SP estimates of
![]() $\unicode[STIX]{x1D702}$
are specification-sensitive: in this particular example, SP with a row-standardized W produces more consistent estimates than SP with an unstandardized W. The density of the latter estimate has a very wide spread, with virtually no peak and long tails extending in both directions.
$\unicode[STIX]{x1D702}$
are specification-sensitive: in this particular example, SP with a row-standardized W produces more consistent estimates than SP with an unstandardized W. The density of the latter estimate has a very wide spread, with virtually no peak and long tails extending in both directions.
Focusing just on the estimates of
![]() $\unicode[STIX]{x1D6FD}_{0}$
and
$\unicode[STIX]{x1D6FD}_{0}$
and
![]() $\unicode[STIX]{x1D6FD}_{1}$
, we see that, applying SP to data generated according to an LSGM process may result in biased or even opposite inferences. Remembering that probit estimates tend to be larger than those of logit, the deflated coefficients on
$\unicode[STIX]{x1D6FD}_{1}$
, we see that, applying SP to data generated according to an LSGM process may result in biased or even opposite inferences. Remembering that probit estimates tend to be larger than those of logit, the deflated coefficients on
![]() $\unicode[STIX]{x1D6FD}_{1}$
recovered by both versions of SP (with and without row standardization of W) are even further from the true values than they appear. Even more disconcertingly, both versions of SP recover a negative coefficient on the intercept
$\unicode[STIX]{x1D6FD}_{1}$
recovered by both versions of SP (with and without row standardization of W) are even further from the true values than they appear. Even more disconcertingly, both versions of SP recover a negative coefficient on the intercept
![]() $\unicode[STIX]{x1D6FD}_{0}$
—a result that is not just biased, but has the wrong sign, given that the true value of
$\unicode[STIX]{x1D6FD}_{0}$
—a result that is not just biased, but has the wrong sign, given that the true value of
![]() $\unicode[STIX]{x1D6FD}_{0}=1$
.
$\unicode[STIX]{x1D6FD}_{0}=1$
.
5 Application: International Alliances
To further demonstrate the benefits of LSGM, we apply it to modeling the formation/duration of the international alliance network. One prominent theory in alliance research suggests that alliances tend to form among states with similar policy orientations (Gibler and Rider Reference Gibler and Rider2004; Lai and Reiter Reference Lai and Reiter2000). The logic is that ideationally similar states will naturally prefer to join their forces to counter a common threat. This reasoning leads to several empirical expectations. If we think of international alliances as network nodes and ideational distances among them as network relationships, then the first expectation is that we should observe that alliances will not be uniformly distributed within the ideational space, but instead will cluster in opposite parts of it. Moreover, there may be a balancing process, in which formation of an alliance in one part of the ideational space will trigger a balancing act in the opposite part of the ideational space (Schweller Reference Schweller2004). As most alliances are multilateral (Gibler and Wolford Reference Gibler and Wolford2006), we may also expect a clustering of alliances within ideational space.
Figure 3 provides a visual demonstration of the modeling approach, and how it differs from more traditional network theories of alliances. Figure 3a shows a traditional visualization of the alliance network with countries as nodes that are connected by edges if the given pair of states were part of an alliance in a given year. Such a visualization corresponds to the traditional theoretical framework common to alliance research—a framework that models alliance formation as a function of state-level (node-level) and dyadic (edge-level) covariates, such as joint democracy, military power or asymmetry, and bilateral trade (Lai and Reiter Reference Lai and Reiter2000). Yet many important theories of alliance formation, such as “birds of a feather,” as well as balancing and bandwagoning, posit processes that cannot be directly modeled using state- and dyad-level attributes—processes that involve alliances (edges) forming in response to other alliances within the network. Modeling these important theoretical processes requires reconceptualizing the alliance network as a network in which alliances themselves are treated as nodes, and relationships among them are treated as edges.

Figure 3. Visualizing International Alliance Formation, 1955. Note: Alliance data are obtained from the Correlates of War Project (Gibler Reference Gibler2009).
Figure 3b demonstrates such a reconceptualization. Each bilateral alliance relationship is represented as a node, that is placed in an ideational Cartesian space in accordance with the ideational scores of each of the two allies that serve as the
![]() $x$
and
$x$
and
![]() $y$
coordinates.Footnote
10
The Euclidean distance between each pair of alliances then serves as a proxy for the ideational dissimilarity between alliances (a continuous conceptualization of a relationship/edge).
$y$
coordinates.Footnote
10
The Euclidean distance between each pair of alliances then serves as a proxy for the ideational dissimilarity between alliances (a continuous conceptualization of a relationship/edge).
This visualization of the international alliance network mimics the theoretical processes posited by the “birds of a feather” theory of alliance formation. Conceptualizing alliances in these terms uncovers a number of dynamics, consistent with this theoretical framework. For example, Figure 3b shows that international alliances tend to form between ideologically similar rather than different states—most alliances cluster close to the diagonal of the graph (the line
![]() $y=x$
would represent the location of all alliance partners with identical ideal scores) rather than in the areas off the diagonal. While this pattern is expected, it is nonetheless useful to be able to confirm this intuition by visualizing the data in a relevant way. Second, Figure 3b highlights clustering in two opposite areas of the ideological space, which is consistent with the balancing logic described above. Third, Figure 3b reveals some insights regarding the ideational cohesion within each of the opposing blocs that formed in the given year: the Soviet bloc consisting of alliances among Russia, Czechoslovakia, Hungary, Poland, and Romania is much more concentrated within the ideational space than the bloc among the United Kingdom, Turkey, Pakistan, Iran, and Iraq.
$y=x$
would represent the location of all alliance partners with identical ideal scores) rather than in the areas off the diagonal. While this pattern is expected, it is nonetheless useful to be able to confirm this intuition by visualizing the data in a relevant way. Second, Figure 3b highlights clustering in two opposite areas of the ideological space, which is consistent with the balancing logic described above. Third, Figure 3b reveals some insights regarding the ideational cohesion within each of the opposing blocs that formed in the given year: the Soviet bloc consisting of alliances among Russia, Czechoslovakia, Hungary, Poland, and Romania is much more concentrated within the ideational space than the bloc among the United Kingdom, Turkey, Pakistan, Iran, and Iraq.
In order to perform a statistical test of the balancing and clustering hypotheses described above, we use international alliance data from the Correlates of War Project (Gibler Reference Gibler2009). The dependent variable is a dichotomous measure of whether a pair of states were part of an alliance in a given year. The estimation sample consists of all politically relevant pairs of states between 1946–2000; the unit of analysis is a network edge (formation/presence of an alliance).
A metric to define connectivity W between alliances is constructed using each partner’s ideal scores based on United Nations General Assembly voting (Bailey, Strezhnev, and Voeten Reference Bailey, Strezhnev and Voeten2015). We treat each potential ally’s ideal score as a coordinate, which allows us to align all potential alliances in a two-dimensional space. Each
![]() $ij$
cell of the W matrix thus contains a measure of the Euclidean distance between
$ij$
cell of the W matrix thus contains a measure of the Euclidean distance between
![]() $i$
and
$i$
and
![]() $j$
in this two-dimensional ideological space. Shorter distances indicate policy similarity while greater distances indicate policy dissimilarity.
$j$
in this two-dimensional ideological space. Shorter distances indicate policy similarity while greater distances indicate policy dissimilarity.
Of course, possible connectivities among alliance edges are not limited to proximity/distance of alliance edges within ideational space. Alternative sources/conceptualization of connectivity among alliances may focus on whether pairs of alliances connect similar states (e.g., two democracies), share a common node, or contain a major power. One may align alliance edges in different types of two-dimensional space, for example, using various state-level attributes as coordinates.
Finally, we include several control variables measured at the state–dyad level. Consistent with prior research, we expect that pairs of states are more likely to be part of a military alliance if they engage in international trade and are jointly democratic (Lai and Reiter Reference Lai and Reiter2000). We also expect that states are more likely to ally if they are approximately even in terms of military capabilities (Kimball Reference Kimball2006). Data on international trade are obtained from the Correlates of War Project (Barbieri, Keshk, and Pollins Reference Barbieri, Keshk and Pollins2009), and data on levels of democracy are obtained from Marshall and Jaggers (Reference Marshall, Gurr and Jaggers2014). Military Power Ratio is measured as the ratio of the military capabilities of the more powerful state in a pair of states to the total military capabilities of the pair, or
![]() $\frac{max(m_{1},m_{2})}{m_{1}+m_{2}}$
. Data on military symmetry/asymmetry are obtained from Arena (Reference Arena2016).
$\frac{max(m_{1},m_{2})}{m_{1}+m_{2}}$
. Data on military symmetry/asymmetry are obtained from Arena (Reference Arena2016).
The results of the estimation are presented in Table 1. The coefficient on Ideational Distance is positive, indicating a balancing process: alliance edges form in response to other alliance edges that realize in an ideationally different part of the network. This finding is consistent with the balancing logic above, in which ideationally similar states balance against the growing power of their adversaries. This resonates with a neoclassical version of the realist balancing theory that qualifies the neorealist balancing hypothesis by highlighting domestic preferences.
Table 1. Applying LSGM to Model International Alliance Formation, 1946–2000. Notes: Standard errors were obtained using a parametric bootstrap with 25050 simulations of complete networks, 50 burnin and 50 iterations for thinning. The simulations were run until additional simulations resulted in only marginal changes in the estimates (the third digit after the decimal point).
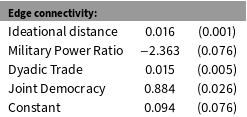
The coefficients on the control variables in both models are as expected. Military Power Ratio has a negative effect, suggesting that, all else held constant, symmetric alliances are more common than asymmetric ones. Dyadic Trade and Joint Democracy have a positive effect, indicating that trade and similar political institutions enhance military cooperation.
6 Application: Formation of Legislative Coalitions
In this section, we demonstrate an empirical application of LSGM to modeling legislative cosponsorships in the Senate of the 107th Congress (2001–2003). We treat each pair of senators as a network edge, which is realized (takes on the value of 1) if two senators cosponsored a piece of legislation; if the pair are not part of a joint cosponsorship, the edge between them is coded as 0. We posit that legislative cosponsorship edges are most likely to form in response to other cosponsorship(s) within the same issue area: thus, legislators from the opposite parties may cosponsor competing pieces of legislation related to the same issue. For example, ideologically liberal senators may cosponsor a bill stipulating an increase in minimum wage in response to a piece of ideologically conservative legislature aimed at relaxing wage standards. Likewise, once a bill on a given issue is introduced, legislators of similar political ideology are likely to form cosponsorships with the original sponsor and each other. In contrast, we may find that, rather than forming two balancing coalitions, members of legislatures cross party lines and cooperate in the middle of the ideational spectrum (Slapin et al. Reference Slapin, Kirkland, Lazzaro, Leslie and O’Grady2017). To zero in on the process of such counterbalancing within an issue area, we narrow our focus to the bills that are broadly related to labor, employment, and pensions, as well as the relevant appropriations decisions, as coded by (Adler and Wilkerson Reference Adler and Wilkerson2006). Data on cosponsorships were obtained from Fowler (Reference Fowler2006a,Reference Fowlerb). Analogous to the alliance example above, cosponsorship edges are treated as located within an ideational space; each cosponsorship is mapped in a Cartesian space using the DWNominate scores of the corresponding pair of senators as coordinates (Poole and Rosenthal Reference Poole and Rosenthal2011).
Table 2. Applying LSGM to Model Senate Cosponsorships. Notes: Standard errors were obtained using a parametric bootstrap via a Gibbs sampler of 1300 complete simulations (50 for burnin and thinning).
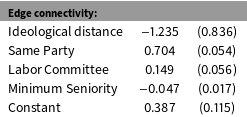
Table 2 presents the results of the estimation. The coefficient on the Ideological Distance is negative and statistically significant: cosponsorships cluster within ideational space. This indicates that cosponsorship behavior is more likely, on average, to happen as a result of bandwagoning than balancing. Most of the control variables act in expected directions. The coefficient on Same Party is positive and statistically significant, suggesting that cosponsorships are more likely among members of the same party. The coefficient on Labor Committee is positive and statistically significant, consistent with the logic that cosponsorships on labor legislation are more likely to happen among a pair of legislators if at least one member of the pair is part of the Health, Education, Labor, and Pensions Senate Committee. The coefficient on Minimum Seniority is negative and statistically significant, which indicates that senior pairs of legislators are less likely to cosponsor legislation than pairs with at least one junior legislator.
This application also provides an opportunity to draw several parallels as well as highlight some trade-offs in inferences that may result from estimating cosponsorship networks using an LSGM vs an ERGM. For example, previous research has employed ERGMs to show that cosponsorship networks are characterized by several higher-order dependencies, such as centrality, reciprocity, and transitivity (Cho and Fowler Reference Cho and Fowler2010; Cranmer and Desmarais Reference Cranmer and Desmarais2011). We discuss LSGM’s treatment of each of these three features, in turn.
Scholars of legislative cosponsorship networks have argued that the network will exhibit a greater than expected average centrality (number of edges per node legislator), as legislators actively seek cosponsors for their bills (Campbell Reference Campbell1982). Within an ERGM, centrality is modeled via an inclusion of the edges parameter—a term analogous to the intercept in a logistic regression, which models the marginal probability of edge formation between each pair of nodes within the network (Strauss and Ikeda Reference Strauss and Ikeda1990; Wasserman and Pattison Reference Wasserman and Pattison1996; Cranmer and Desmarais Reference Cranmer and Desmarais2011). LSGM’s analogue to the edges parameter in ERGMs is the
![]() $\unicode[STIX]{x1D705}_{i}$
parameter in Equation 2 above, which models the marginal probability of each edge
$\unicode[STIX]{x1D705}_{i}$
parameter in Equation 2 above, which models the marginal probability of each edge
![]() $i$
as a function of exogenous covariates
$i$
as a function of exogenous covariates
![]() $X_{i}$
(Kaiser, Caragea, and Furukawa Reference Kaiser, Caragea and Furukawa2012). Thus, Figure 4 shows a histogram of the degree distribution in the observed cosponsorship data, overlapped with a kernel density distribution of degree in 100 networks predicted using LSGM estimates (from Table 2). We can see that the degree distribution in the predicted data has a reasonably good fit to the observed data.
$X_{i}$
(Kaiser, Caragea, and Furukawa Reference Kaiser, Caragea and Furukawa2012). Thus, Figure 4 shows a histogram of the degree distribution in the observed cosponsorship data, overlapped with a kernel density distribution of degree in 100 networks predicted using LSGM estimates (from Table 2). We can see that the degree distribution in the predicted data has a reasonably good fit to the observed data.
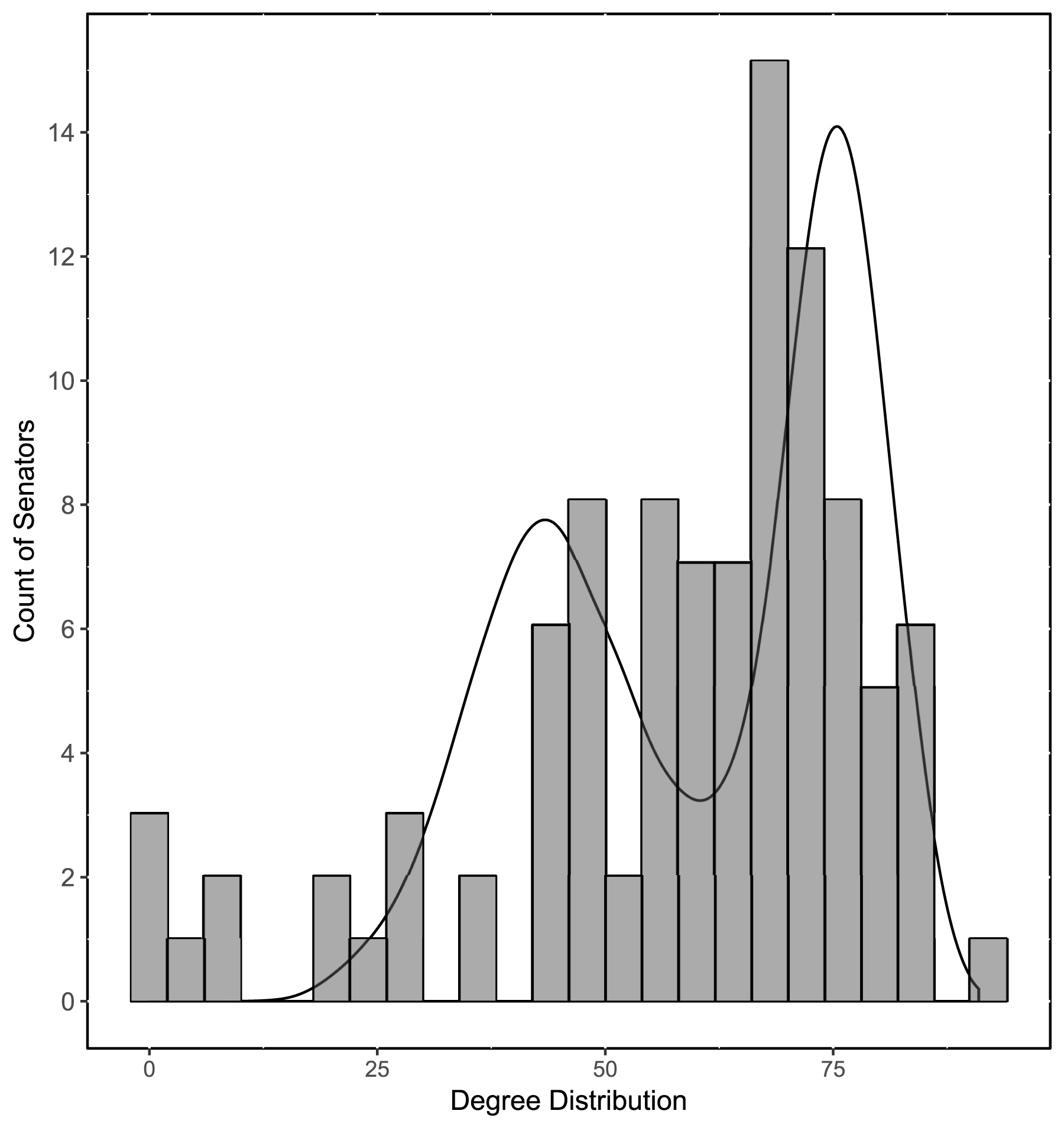
Figure 4. Degree distributions in the observed and simulated graphs.
The term Reciprocity is typically used for modeling individual legislator’s decisions to cosponsor legislation (i.e., legislator
![]() $A$
may be more likely to cosponsor a bill by legislator
$A$
may be more likely to cosponsor a bill by legislator
![]() $B$
if
$B$
if
![]() $B$
cosponsors a bill proposed by
$B$
cosponsors a bill proposed by
![]() $A$
). In such applications, cosponsorship edges are directed, that is, edge
$A$
). In such applications, cosponsorship edges are directed, that is, edge
![]() $AB$
is different from edge
$AB$
is different from edge
![]() $BA$
(e.g., Cranmer and Desmarais Reference Cranmer and Desmarais2011). In our application, however, we are interested in a slightly different aspect of cosponsorship—we treat cosponsorship as a proxy of cooperation to model diffusion of cooperation in the Senate (does edge
$BA$
(e.g., Cranmer and Desmarais Reference Cranmer and Desmarais2011). In our application, however, we are interested in a slightly different aspect of cosponsorship—we treat cosponsorship as a proxy of cooperation to model diffusion of cooperation in the Senate (does edge
![]() $AB$
affect the probability of other edges among ideationally similar legislators?). As a result, our focus is the act of cosponsorship itself, rather than its direction: in our application, cosponsorship is an undirected edge.Footnote
11
$AB$
affect the probability of other edges among ideationally similar legislators?). As a result, our focus is the act of cosponsorship itself, rather than its direction: in our application, cosponsorship is an undirected edge.Footnote
11
Finally, though transitivity (i.e., the cosponsorship network’s tendency to form triangles) is not currently explicitly incorporated within an LSGM, we can assess LSGM’s ability to reflect the amount of transitivity observed in data by calculating two additional measures: the average number of triangles and the proportion of correctly predicted triangles in a 100 networks simulated using LSGM estimates (from Table 2). We find that, although LSGM does not fare well on the first measure (on, average, predicted networks exhibit about twice as many triangles as the observed data), it fares reasonably well in terms of correctly predicting triangles in the observed data—the average percent of correctly predicted triangles in 100 simulated networks is around 87% (although this number is somewhat inflated as a result of LSGM’s tendency to overpredict the number of triangles in the data). Taken together, even when it comes to implicit modeling of network features, LSGM continues to perform reasonably well on its primary goal of modeling localized rather than global structures within the network. Conversely, while an ERGM would correctly model the number of triangles at the global level, any networks predicted from an ERGM would exhibit a low rate of correctly predicted triangles (as ERGMs are usually not specified to model local structures within the network).
The application of LSGM to modeling legislative cosponsorships, therefore, helps highlight an important trade-off: while the omission of the Triangles term from the cosponsorship example may result in specification bias, a failure to model localized processes may result in a different type of specification bias, as well as obscure important inferences regarding the formation of a network. Thus, researchers whose primary interest is in modeling global higher-order dependencies in the network may want to estimate an ERGM, whereas an LSGM is more suitable for researchers who are interested in modeling localized dependencies. Finally, reformulating LSGM to explicitly model higher-order dependencies, such as Triangles is a useful direction for future work.
7 Conclusion
This paper introduces an LSGM—a statistical estimator designed for modeling the formation of local structures within networks. We demonstrated the desirable asymptotic properties of the estimator using Monte Carlo simulations and provided two illustrative applications to modeling the formation of the international alliance network and legislative coalitions. More broadly, we emphasized the narrowness and inflexibility of the traditional network focus on actors as nodes and relationships among them as edges. Adopting more flexible assumptions of what constitutes nodes and edges helps model many localized network processes, such as balancing, bandwagoning, and cascades.
LSGM provides an alternative to other types of network and spatial models used within the field of political science. The key difference between LSGM and spatial econometric models (e.g., SAR, spatial probit) has to do with the theoretical process being modeled. Econometric models of dependence assume a long-term and iterative process that operates through self-loops: an outcome in location
![]() $i$
is a function of the outcomes of
$i$
is a function of the outcomes of
![]() $i$
’s neighbors, the neighbors of
$i$
’s neighbors, the neighbors of
![]() $i$
’s neighbors, and so on, and also
$i$
’s neighbors, and so on, and also
![]() $i$
’s own (indirect) effect on its neighbors and its neighbor’s neighbors, and so on. In contrast, LSGM posits a much simpler theoretical process, in which the dependence in outcomes stops at the neighbors of the first degree, that is, any higher-order dependence is assumed to simply strengthen/alleviate the effect of first-order dependence. According to the theoretical process posited by LSGM and, more generally, by Markov random field models, the outcome in
$i$
’s own (indirect) effect on its neighbors and its neighbor’s neighbors, and so on. In contrast, LSGM posits a much simpler theoretical process, in which the dependence in outcomes stops at the neighbors of the first degree, that is, any higher-order dependence is assumed to simply strengthen/alleviate the effect of first-order dependence. According to the theoretical process posited by LSGM and, more generally, by Markov random field models, the outcome in
![]() $i$
is a function of the outcomes in
$i$
is a function of the outcomes in
![]() $i$
’s neighbors only, with any secondary effects of the neighbors of
$i$
’s neighbors only, with any secondary effects of the neighbors of
![]() $i$
’s neighbors simply enhancing/weakening the effect of
$i$
’s neighbors simply enhancing/weakening the effect of
![]() $i$
’s neighbors. Ultimately, the choice of the estimator, therefore, must be dictated by the specifics of the particular empirical application in question. The second advantage of an LSGM/CAR over a SAR is the relative ease of interpretation of the dependence parameter as directly proportional to the log odds ratio of the presence of an edge, relative to an independence model, in which each edge forms with a probability 0.5, holding all else constant.
$i$
’s neighbors. Ultimately, the choice of the estimator, therefore, must be dictated by the specifics of the particular empirical application in question. The second advantage of an LSGM/CAR over a SAR is the relative ease of interpretation of the dependence parameter as directly proportional to the log odds ratio of the presence of an edge, relative to an independence model, in which each edge forms with a probability 0.5, holding all else constant.
LSGM has many potential applications to modeling information diffusion, or tipping-point processes, such as community outreach related to building support for a particular policy. The proposed framework easily extends to modeling localized formation of other types of network structures, such as triangles or
![]() $k$
-stars, albeit the theoretical mechanisms behind such processes are currently underdeveloped. The LSGM provides a tool for testing for such dependencies in a controlled, interpretable way.
$k$
-stars, albeit the theoretical mechanisms behind such processes are currently underdeveloped. The LSGM provides a tool for testing for such dependencies in a controlled, interpretable way.
A direction for future research is to derive the conditions under which an LSGM can simultaneously incorporate several overlapping sources of dependence among units—a feature that would make LSGM even more attractive to social scientists. This particular property of LSGM or any other types of Markov random field models has not been explored in statistics (i.e., it has not been shown that there exists a joint distribution that corresponds to the specified conditionals involved in a formulation of an LSGM with more than one overlapping neighborhood/connectivity).Footnote 12 We suspect that a lack of research in this direction is purely due to LSGM’s origin from statistical literature with most common applications to medicine (e.g., cancer research) or biology (e.g., spread of plant diseases), where modeling multiple connectivities is rarely of interest.
Appendix
In this section, we perform a Monte Carlo experiment to explore LSGM and SP’s performance in the presence of measurement bias in W. We start with simulating 500 networks according to an LSGM DGP and 500 different networks according to a SP DGP, following exactly the same processes as in Section 4 of the manuscript and holding X, W, and all the parameters at fixed valuesFootnote
13
. Next, to generate two different types of bias in the W, we perturbed the original W matrix in two separate ways: (1) multiplied the top largest 40% of
![]() $ij$
values in W by 1.5 and (2) multiplied the top largest 40% of
$ij$
values in W by 1.5 and (2) multiplied the top largest 40% of
![]() $ij$
values in W by 1.5 while also adding random error,
$ij$
values in W by 1.5 while also adding random error,
![]() $\unicode[STIX]{x1D716}_{ij}\sim N(4,1)$
.Footnote
14
Finally, we estimated an LSGM and SP (each on the 500 networks generated according to their own DGP) using the original W and each version of the perturbed W’s. The results are presented in Figure 5.
$\unicode[STIX]{x1D716}_{ij}\sim N(4,1)$
.Footnote
14
Finally, we estimated an LSGM and SP (each on the 500 networks generated according to their own DGP) using the original W and each version of the perturbed W’s. The results are presented in Figure 5.
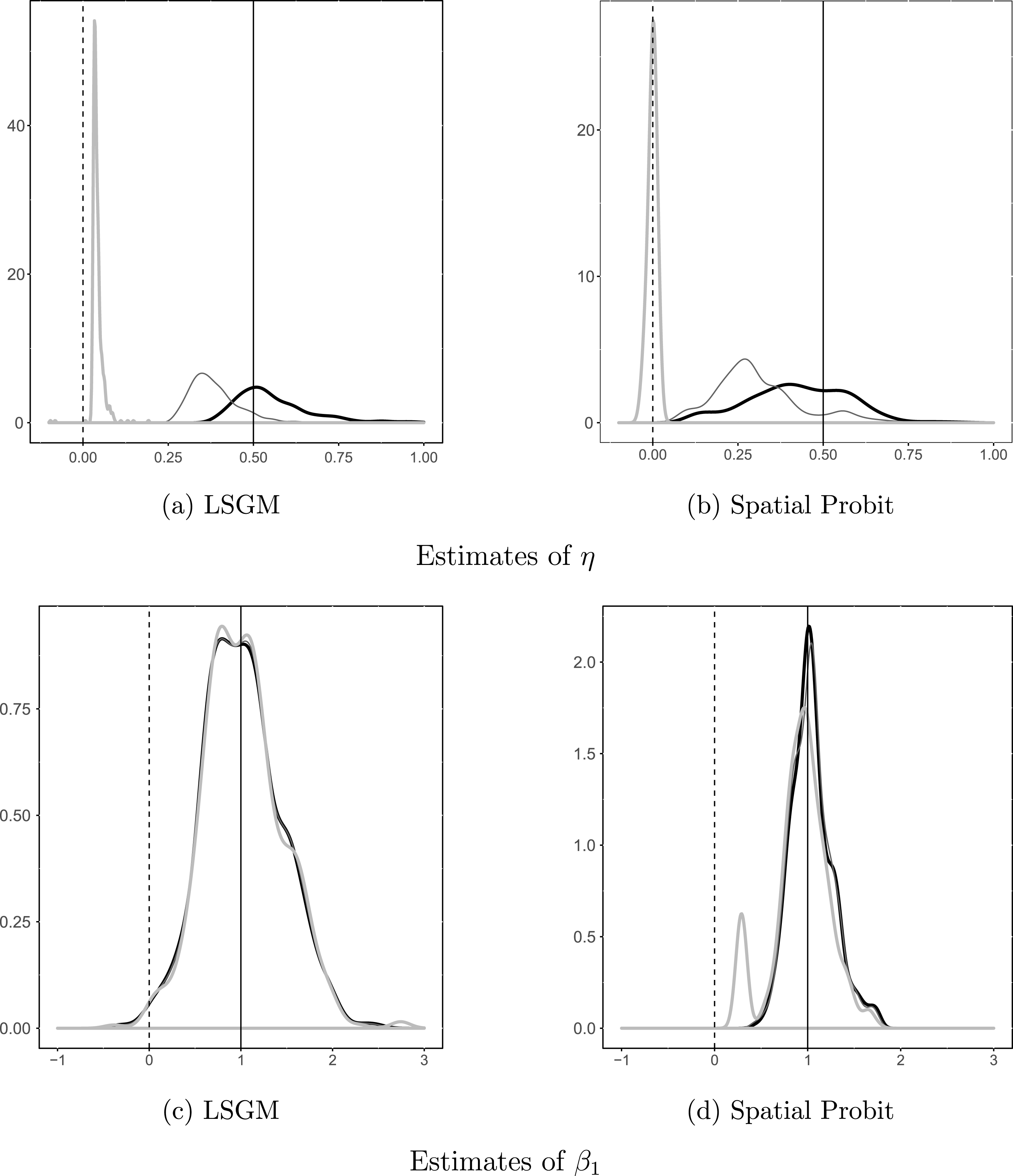
Figure 5. The effect of bias in the connectivity matrix, W, on estimates of LSGM and spatial probit. Notes: Estimates are obtained as a result of 500 simulations of complete networks, according to the data-generating process of each estimator. Black curves represent the kernel density estimates on data with no bias in the connectivity matrix W, dark gray curves represent estimates on data with benign (rescaling) bias in W, and light gray curves represent estimates on data with severe bias in W. Vertical lines show the true values; dashed lines denote 0.
We can make several observations by looking at these results. First, both models are relatively robust to the first type of bias in W (rescaling the top largest 40% of cell entries by 1.5): both models return correctly signed, although deflated (closer to 0), coefficients on
![]() $\unicode[STIX]{x1D702}$
; and both models are spot-on on the coefficient
$\unicode[STIX]{x1D702}$
; and both models are spot-on on the coefficient
![]() $\unicode[STIX]{x1D6FD}_{1}$
. In the presence of the second type of bias in W (rescaling and adding error to the top largest 40% of cell entries), LSGM continues to produce the correct inference about the effect of
$\unicode[STIX]{x1D6FD}_{1}$
. In the presence of the second type of bias in W (rescaling and adding error to the top largest 40% of cell entries), LSGM continues to produce the correct inference about the effect of
![]() $\unicode[STIX]{x1D702}$
(
$\unicode[STIX]{x1D702}$
(
![]() $\unicode[STIX]{x1D702}$
is still positive, although even more deflated), while SP’s estimates of
$\unicode[STIX]{x1D702}$
is still positive, although even more deflated), while SP’s estimates of
![]() $\unicode[STIX]{x1D702}$
center around zero. We also see that, in the presence of the second types of bias, SP becomes less efficient at recovering the correct value of
$\unicode[STIX]{x1D702}$
center around zero. We also see that, in the presence of the second types of bias, SP becomes less efficient at recovering the correct value of
![]() $\unicode[STIX]{x1D6FD}_{1}$
(notice the secondary bump in the kernel density), while LSGM continues to recover the correct value of
$\unicode[STIX]{x1D6FD}_{1}$
(notice the secondary bump in the kernel density), while LSGM continues to recover the correct value of
![]() $\unicode[STIX]{x1D6FD}_{1}$
.
$\unicode[STIX]{x1D6FD}_{1}$
.









