Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T14:31:33.043Z Has data issue: false hasContentIssue false
  • English
  • Français

A Bounds Approach to Inference Using the Long Run Multiplier

Published online by Cambridge University Press:  22 March 2019

Clayton Webb Open the ORCID record for Clayton Webb [Opens in a new window] ,
Suzanna Linn Open the ORCID record for Suzanna Linn [Opens in a new window]  and
Matthew Lebo
Clayton Webb*
Affiliation:
Department of Political Science, University of Kansas, Lawrence, KS 66045, USA. Email: [email protected]
Suzanna Linn
Affiliation:
Department of Political Science, Pennsylvania State University, State College, PA 16802, USA. Email: [email protected]
Matthew Lebo
Affiliation:
Department of Political Science, Stony Brook University, Stony Brook, NY 11794, USA. Email: [email protected]
*
*Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Pesaran, Shin, and Smith (2001) (PSS) proposed a bounds procedure for testing for the existence of long run cointegrating relationships between a unit root dependent variable (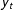$y_{t}$) and a set of weakly exogenous regressors $\boldsymbol{x}_{t}$ when the analyst does not know whether the independent variables are stationary, unit root, or mutually cointegrated processes. This procedure recognizes the analyst’s uncertainty over the nature of the regressors but not the dependent variable. When the analyst is uncertain whether 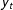$y_{t}$ is a stationary or unit root process, the test statistics proposed by PSS are uninformative for inference on the existence of a long run relationship (LRR) between 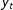$y_{t}$ and 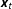$\boldsymbol{x}_{t}$. We propose the long run multiplier (LRM) test statistic as a means of testing for LRRs without knowing whether the series are stationary or unit roots. Using stochastic simulations, we demonstrate the behavior of the test statistic given uncertainty about the univariate dynamics of both 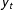$y_{t}$ and 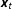$\boldsymbol{x}_{t}$, illustrate the bounds of the test statistic, and generate small sample and approximate asymptotic critical values for the upper and lower bounds for a range of sample sizes and model specifications. We demonstrate the utility of the bounds framework for testing for LRRs in models of public policy mood and presidential success.

Keywords

time seriesunit root testbounds testcointegration
Type
Articles
Information
Political Analysis , Volume 27 , Issue 3 , July 2019 , pp. 281 - 301
Copyright
Copyright © The Author(s) 2019. Published by Cambridge University Press on behalf of the Society for Political Methodology. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Jeff Gill

Authors’ note: The authors are grateful to John Freeman and the anonymous reviewers for their thoughtful comments. We would also like to thank Paul Johnson and Dave Armstrong for their help with computing and feedback on the simulation designs. We thank the Center for Research Methods and Data Analysis and the College of Liberal Sciences at the University of Kansas for access to their high performance compute cluster on which many of the calculations reported here were conducted. Replication materials can be found at Webb, Linn, and Lebo (2018).

References

Aldrich, J. H., Berger, M. M., and Rohde, D. W.. 2002. “The Historical Variability in Conditional Party Government, 1874–1944.” In Party, Process, and Political Change in Congress , edited by Brady, D. W. and McCubbins, M. D., 17–35. Stanford, CA: Stanford University Press.Google Scholar
Baker, A. 2015. “Public Mood and Presidential Outcomes in Mexico.” In Mexico’s Evolving Democracy: A Comparative Study of the 2012 Elections , edited by Dominguez, J. I., Greene, K. F., Lawson, C. H., and Moreno, A., 107–127. Baltimore, MD: Johns Hopkins University Press.Google Scholar
Banerjee, A., Dolado, J., and Mestre, R.. 1998. “Error-Correction Mechanism Tests for Cointegration in a Single-Equation Framework.” Journal of Time Series Analysis 19(3):267–283.Google Scholar
Banerjee, A. A., Dolado, J., Galbraith, J. W., and Hendry, D. F.. 1993. Co-Integration, Error Correction, and the Econometric Analysis of Non-Stationary Data . Oxford: Oxford University Press.Google Scholar
Bartle, J., Bosch, A., and Orriols, L.. 2014. “The Spanish Policy Mood, 1978–2012.” In 8th ECPR General Conference , 3–6. Glasgow: University of Glasgow.Google Scholar
Bartle, J., Dellepiane-Avellaneda, S., and Stimson, J.. 2011. “The Moving Centre: Preferences for Government Activity in Britain, 1950–2005.” British Journal of Political Science 41(2):259–285.Google Scholar
Benjamin, D. J., Berger, J. O., Johannesson, M., Nosek, B. A., Wagenmakers, E.-J., Berk, R., Bollen, K. A., Brembs, B., Brown, L., and Camerer, C. et al. . 2018. “Redefine Statistical Significance.” Nature Human Behaviour 2(1):6–10.Google Scholar
Bewley, R. A. 1979. “The Direct Estimation of the Equilibrium Response in a Linear Model.” Economic Letters 3:357–361.Google Scholar
Bond, J. R., and Fleisher, R.. 1984. “Presidential Popularity and Congressional Voting: A Reexamination of Public Opinion as a Source of Influence in Congress.” Western Political Quarterly 37(2):291–306.Google Scholar
Box-Steffensmeier, J. M., Freeman, J. R., Hitt, M. P., and Pevehouse, J. C.. 2014. Time Series Analysis for the Social Sciences . New York: Cambridge University Press.Google Scholar
Box-Steffensmeier, J. M., and Smith, R. M.. 1996. “The Dynamics of Aggregate Partisanship.” American Political Science Review 90(3):567–580.Google Scholar
Brouard, S., and Guinaudeau, I.. 2015. “Policy Beyond Politics? Public Opinion, Party Politics and the French Pro-Nuclear Energy Policy.” Journal of Public Policy 35(1):137–170.Google Scholar
Campbell, J. Y., and Perron, P.. 1991. “Pitfalls and Opportunities: What Macroeconomists Should Know About Unit Roots.” NBER Macroeconomics Annual 6:141–201.Google Scholar
Cavaliere, G., and Xu, F.. 2014. “Testing for Unit Roots in Bounded Time Series.” Journal of Econometrics 178(2):259–272.Google Scholar
Choi, I. 2015. Almost All About Unit Roots . New York: Cambridge University Press.Google Scholar
De Boef, S., and Granato, J.. 1997. “Near-Integrated Data and the Analysis of Political Relationship.” American Journal of Political Science 41(2):619–640.Google Scholar
De Boef, S., and Keele, L.. 2008. “Taking Time Seriously.” American Journal of Political Science 52(1):184–200.Google Scholar
Dejong, D. N., Nankervis, J. C., Savin, N. E., and Whiteman, C. H.. 1992. “The Power Problems of Unit Root Test in Time Series With Autoregressive Errors.” Journal of Econometrics 53(1–3):323–343.Google Scholar
Dickey, D. A., and Fuller, W. A.. 1979. “Distribution of the Estimators for Autoregressive Time Series With a Unit Root.” Journal of the American Statistical Association 74:427–431.Google Scholar
Dickinson, M. J., and Lebo, M. J.. 2007. “Reexamining the Growth of the Institutional Presidency, 1940–2000.” Journal of Politics 69(1):206–219.Google Scholar
Durr, R. H. 1992. “Of Forests and Trees.” Political Analysis 4:255–258.Google Scholar
Durr, R. H. 1993. “What Moves Policy Sentiment? American Political Science Review 87(1):158–170.Google Scholar
Edwards, G. C. 2009. The Strategic President . Princeton, NJ: Princeton University Press.Google Scholar
Elliott, G., Rothenberg, T., and Stock, J. H.. 1996. “Efficient Tests for an Autoregressive Unit Root.” Econometrics 64:813–836.Google Scholar
Ellis, C. R., and Faricy, C.. 2011. “Social Policy and Public Opinion: How the Ideological Direction of Spending Influences Public Mood.” The Journal of Politics 73(4):1095–1110.Google Scholar
Engle, R. F., and Granger, C. W. J.. 1987. “Co-Integration and Error Correction: Representation, Estimation, and Testing.” Econometrica 55:251–276.Google Scholar
Enns, P. K., and Kellstedt, P. M.. 2008. “Policy Mood and Political Sophistication: Why Everybody Moves Mood.” British Journal of Political Science 38(3):433–454.Google Scholar
Enns, P. K., and Wlezien, C.. 2017. “Understanding Equation Balance in Time Series Regression.” The Political Methodologist 24(2):2–12.Google Scholar
Ericsson, N. R., and MacKinnon, J. G.. 2002. “Distributions of Error Correction Tests for Cointegration.” The Econometrics Journal 5(2):285–318.Google Scholar
Erikson, R. S., MacKuen, M. B., and Stimson, J. A.. 2002. The Macro Polity . New York: Cambridge University Press.Google Scholar
Esarey, J.2017. “Lowering the Threshold of Statistical Significance to $p<0.005$ to Encourage Enriched Theories of Politics.” The Political Methodologist, August 7. https://thepoliticalmethodologist.com/2017/08/07/in-support-of-enriched-theories-of-politics-a-case-for-lowering-the-threshold-of-statistical-significance-to-p-0-005/.Google Scholar
Evans, G., and Savin, N. E.. 1981. “Testing for Unit Roots: 1.” Econometrica: Journal of the Econometric Society 49(3):753–779.Google Scholar
Evans, G., and Savin, N.. 1984. “Testing for Unit Roots: 2.” Econometrica: Journal of the Econometric Society 52(5):1241–1269.Google Scholar
EViews. 2017. “AutoRegressive Distributed Lag (ARDL) Estimation. Part 2—Inference.” EViews, May 8. http://blog.eviews.com/2017/05/autoregressive-distributed-lag-ardl_8.html#mjx-eqn-eq.ardl.20.Google Scholar
Ferguson, G., Kellstedt, P. M., and Linn, S.. 2013. “How Does the Economy Shape Policy Preferences? Electoral Studies 32(3):544–550.Google Scholar
Granger, C. W., and Newbold, P.. 1974. “Spurious Regression in Econometrics.” Journal of Econometrics 2(2):111–120.Google Scholar
Grant, T., and Lebo, M. J.. 2016. “Error Correction Methods with Political Time Series.” Political Analysis 24(1):3–30.Google Scholar
Green, J., and Jennings, W.. 2012. “Valence as Macro-Competence: An Analysis of Mood in Party Competence Evaluations in Great Britain.” British Journal of Political Science 42(2):311–343.Google Scholar
Greene, W. H. 2017. Econometric Analysis . 8th ed. New York: Pearson.Google Scholar
Hendry, D. F. 1995. Dynamic Econometrics . Oxford: Oxford University Press.Google Scholar
Juhl, T., and Xiao, Z.. 2003. “Power Functions and Envelopes for Unit Root Tests.” Econometric Theory 19(2):240–253.Google Scholar
Kwiatkowski, D., Phillips, P., Schmidt, P., and Shin, Y.. 1992. “Testing the Null Hypothesis of Stationarity Against the Alternative of a Unit Root.” Journal of Econometrics 54:159–178.Google Scholar
Lebo, M. J., and Grant, T.. 2016. “Equation Balance and Dynamic Political Modeling.” Political Analysis 24(1):69–82.Google Scholar
Lebo, M. J., and Kraft, P. W.. 2017. “The General Error Correction Model in Practice.” Research & Politics 4(2): 2053168017713059.Google Scholar
Lebo, M. J., and O’Geen, A. J.. 2011. “The President’s Role in the Partisan Congressional Arena.” The Journal of Politics 73(3):718–734.Google Scholar
Lebo, M. J., Walker, R. W., and Clarke, H. D.. 2000. “You Must Remember This: Dealing with Long Memory in Political Analyses.” Electoral Studies 19(1):31–48.Google Scholar
Narayan, P. K. 2005. “The Saving and Investment Nexus for China: Evidence from Cointegration Tests.” Applied Economics 37(17):1979–1990.Google Scholar
Neustadt, R. E. 1960. Presidential Power . New York, NY: Wiley.Google Scholar
Ornstein, N. J., Mann, T. E., and Malbin, M. J.. 2008. Vital Statistics on Congress 2008 . Washington, DC: Brookings Institution Press.Google Scholar
Ostrom, C. W. Jr., and Simon, D. M.. 1985. “Promise and Performance: A Dynamic Model of Presidential Popularity.” American Political Science Review 79(2):334–358.Google Scholar
Owen, E., and Quinn, D. P.. 2016. “Does Economic Globaliszation Influence the US Policy Mood? A Study of US Public Sentiment 1956–2011.” British Journal of Political Science 46(1):95–125.Google Scholar
Perron, P., and Ng, S.. 1996. “Useful Modifications to Some Unit Root Tests with Dependent Errors and Their Local Asymptotic Properties.” The Review of Economic Studies 63(3):435–463.Google Scholar
Pesaran, M. H., and Shin, Y.. 1998. “An Autoregressive Distributed-Lag Modelling Approach to Cointegration Analysis.” Econometric Society Monographs 31:371–413.Google Scholar
Pesaran, M. H., Shin, Y., and Smith, R. J.. 2001. “Bounds Testing Approaches to the Analysis of Level Relationships.” Journal of Applied Econometrics 16(3):289–326.Google Scholar
Pesaran, M. H., and Smith, R. P.. 1998. “Structural Analysis of Cointegrating Vars.” Journal of Economic Surveys 12(5):471–505.Google Scholar
Philips, A. Q. 2018. “Have Your Cake and Eat it Too? Cointegration and Dynamic Inference From Autoregressive Distributed Lag Models.” American Journal of Political Science 62(1):230–244.Google Scholar
Stimson, J. A. 1991. Public Opinion in America: Moods, Cycles, and Swings . Boulder, CO: Westview Press.Google Scholar
Stimson, J. A. 1998. Public Opinion in America: Moods, Cycles, and Swings . 2nd ed. Boulder, CO: Westview Press.Google Scholar
Stimson, J. A., Thiebaut, C., and Tiberj, V.. 2012. “The Evolution of Policy Attitudes in France.” European Union Politics 13(2):293–316.Google Scholar
Stimson, J. A., Tiberj, V., and Thiébaut, C.. 2010. “Au Service de l’Analyse Dynamique des Opinions.” Revue française de science politique 60(5):901–926.Google Scholar
Stock, J. H. 1991. “Confidence Intervals for the Largest Autoregressive Root in US Macroeconomic Time Series.” Journal of Monetary Economics 28(3):435–459.Google Scholar
Webb, C., Linn, S., and Lebo, M.. 2018. “Replication Data for: A Bounds Approach to Inference Using the Long Run Multiplier.” https://doi.org/10.7910/DVN/4RCPSE, Harvard Dataverse, V1.Google Scholar
Wlezien, C. 1995. “The Public as Thermostat: Dynamics of Preferences for Spending.” American Journal of Political Science 39(4):981–1000.Google Scholar
Supplementary material: File

Webb et al. supplementary material

Appendix

Download Webb et al. supplementary material(File)
File 34.6 KB