Article contents
A Bounds Approach to Inference Using the Long Run Multiplier
Published online by Cambridge University Press: 22 March 2019
Abstract
Pesaran, Shin, and Smith (2001) (PSS) proposed a bounds procedure for testing for the existence of long run cointegrating relationships between a unit root dependent variable (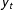 $y_{t}$) and a set of weakly exogenous regressors
$y_{t}$) and a set of weakly exogenous regressors  $\boldsymbol{x}_{t}$ when the analyst does not know whether the independent variables are stationary, unit root, or mutually cointegrated processes. This procedure recognizes the analyst’s uncertainty over the nature of the regressors but not the dependent variable. When the analyst is uncertain whether
$\boldsymbol{x}_{t}$ when the analyst does not know whether the independent variables are stationary, unit root, or mutually cointegrated processes. This procedure recognizes the analyst’s uncertainty over the nature of the regressors but not the dependent variable. When the analyst is uncertain whether 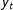 $y_{t}$ is a stationary or unit root process, the test statistics proposed by PSS are uninformative for inference on the existence of a long run relationship (LRR) between
$y_{t}$ is a stationary or unit root process, the test statistics proposed by PSS are uninformative for inference on the existence of a long run relationship (LRR) between 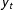 $y_{t}$ and
$y_{t}$ and 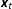 $\boldsymbol{x}_{t}$. We propose the long run multiplier (LRM) test statistic as a means of testing for LRRs without knowing whether the series are stationary or unit roots. Using stochastic simulations, we demonstrate the behavior of the test statistic given uncertainty about the univariate dynamics of both
$\boldsymbol{x}_{t}$. We propose the long run multiplier (LRM) test statistic as a means of testing for LRRs without knowing whether the series are stationary or unit roots. Using stochastic simulations, we demonstrate the behavior of the test statistic given uncertainty about the univariate dynamics of both 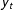 $y_{t}$ and
$y_{t}$ and 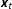 $\boldsymbol{x}_{t}$, illustrate the bounds of the test statistic, and generate small sample and approximate asymptotic critical values for the upper and lower bounds for a range of sample sizes and model specifications. We demonstrate the utility of the bounds framework for testing for LRRs in models of public policy mood and presidential success.
$\boldsymbol{x}_{t}$, illustrate the bounds of the test statistic, and generate small sample and approximate asymptotic critical values for the upper and lower bounds for a range of sample sizes and model specifications. We demonstrate the utility of the bounds framework for testing for LRRs in models of public policy mood and presidential success.
- Type
- Articles
- Information
- Copyright
- Copyright © The Author(s) 2019. Published by Cambridge University Press on behalf of the Society for Political Methodology.
Footnotes
Contributing Editor: Jeff Gill
Authors’ note: The authors are grateful to John Freeman and the anonymous reviewers for their thoughtful comments. We would also like to thank Paul Johnson and Dave Armstrong for their help with computing and feedback on the simulation designs. We thank the Center for Research Methods and Data Analysis and the College of Liberal Sciences at the University of Kansas for access to their high performance compute cluster on which many of the calculations reported here were conducted. Replication materials can be found at Webb, Linn, and Lebo (2018).
References
- 12
- Cited by


