Parallelism within serialism: primary stress is different

Abstract

Primary word stress is typologically diverse. In some languages, the metrical structure of a word predicts the location of primary stress, while in other languages it does not. This diversity is considered through the lens of Harmonic Serialism (HS), a serial constraint-based theory, and it is argued that HS must incorporate a limited degree of parallelism to capture the typology. Namely, primary-stress assignment is simultaneous with foot-building and also mobile, being (re)assessed throughout a metrical derivation. But incorporating this parallelism into HS is both possible and desirable: the positive typological consequences of HS are preserved, and the implied formal divergence between the prosodic word and the foot with respect to parallelism echoes a fundamental distinction that is visible in a wide range of extant theoretical and empirical findings.

1 Introduction

Primary stress is a cross-linguistically heterogeneous category. The primary or main stress is the strongest stress within a given prosodic domain (here, the word), and it instantiates the property of culminativity, in the sense that the metrical structure ‘culminates’ in a single, strongest stress peak (Hyman 1977, Prince 1983, Hayes 1995 and others). In many languages with iterative stress, the direction of primary-stress alignment coincides with the origin of foot iteration, and the primary stress occupies a foot type that looks the same as non-primary stress feet (Hammond 1985a, b, Hayes 1995). But asymmetries between primary and non-primary stresses are also robustly attested, as found, for example, in the work of Odden (1979), Bailey (1995), Hayes (1995), Hurch (1996), McGarrity (2003) and Goedemans & van der Hulst (2014).

This paper considers the implications of this empirical diversity (which will be reviewed in detail in §2) specifically for the theory of primary stress, and more generally for metrical and prosodic theory. I will argue that the typology of asymmetric primary/non-primary stress patterns points to the need for parallelism in the grammar – that primary stress must be able to both affect and be affected by non-primary stresses or general foot structure. I will make my case by showing that accounting for the full range of primary stress patterns in Harmonic Serialism (HS) (Prince & Smolensky 2004, McCarthy 2010, 2016) – a serial constraint-based theory of phonology – requires two assumptions about the candidate-generation function Gen: first, the primary stress must be assigned to the first foot in a derivation and, second, it must be continually reassessed throughout a derivation by admitting candidates with primary stress movement. However, I will also argue that this parallelism is modular, in the sense that there is no contradiction – either theoretically or empirically – in allowing primary stress parallelism while enforcing serialism at the level of feet and between foot construction and segmental operations. There is now ample evidence for this kind of serialism, which will also be reviewed. Taken together, these points culminate in the claim that primary stress is different: while extant evidence for foot construction and foot-based processes points to serialism, primary stress nonetheless requires parallelism. Although work in phonological theory has tended to debate parallelism vs. serialism in terms of the structure of grammar, the view from primary stress will suggest that it is best seen as a process-specific determination.

In the next section, I lay the groundwork for the proposal by summarising and illustrating the typology of primary stress, reviewing extant evidence for HS and presenting an overview of the challenges encountered in squaring these two sets of findings. §3 then gives this paper's main proposal for parallelism in primary stress. §4 and §5 present detailed case studies in light of the proposal and a rejection of alternative HS analyses that do not invoke parallelism. §6 compares parallel Optimality Theory with the version of HS advocated here and draws on existing literature to marshal further evidence that primary stress is different. §7 concludes.

2 Background

2.1 The typological landscape of primary stress

In languages with iterative stress, we often find that the primary stress is anchored at the ‘start’ of the metrical parse (e.g. Hammond 1985a,b; Hayes 1995). The data below illustrate this with the well-known examples of Pintupi (Pama-Nyungan, Australia; Hansen & Hansen 1969) and Warao (Language isolate, Venezuela; Osborn 1966). In Pintupi, stress appears on odd-numbered syllables counting from the left, the leftmost of which is primary. In Warao, stress iterates on even-numbered syllables right-to-left, with primary stress on the rightmost syllable. In both cases, a foot-based analysis straightforwardly posits quantity-insensitive trochees, and the direction of foot alignment matches that of primary-stress alignment (left for Pintupi, right for Warao). This results in a fixed position for the primary stress (initial in Pintupi, penult in Warao).¹

A crucial feature of the Pintupi/Warao type of stress pattern is a kind of symmetry or convergence between primary stress and the general metrical structure of the word, evidenced here by non-primary stresses.² In these kinds of languages, primary stress both predicts and is predictable from non-primary stresses. Although this pattern is prevalent, typological work has also revealed cases where the primary stress relates to the general metrical structure of a word in different ways, resulting in primary/non-primary stress generalisations that are asymmetric or divergent (e.g. Odden 1979, Hayes 1995, McGarrity 2003, Goedemans & van der Hulst 2014). In some cases, the divergence is relatively superficial, such as when segmental processes such as vowel lengthening apply selectively to the primary stressed syllable but not to other stressed syllables (Hayes 1995, McGarrity 2003). In many other cases, however, the divergence is integral to the statement of the stress pattern itself. Such cases can be divided into two categories: those where the primary stress is autonomous from general metrical structure and those where primary stress is parasitic on general metrical structure. Both are exemplified briefly in this section and given fuller treatment in §§4-5. In previous literature, a similar distinction has been identified between languages with ‘top-down’ stress and those with ‘bottom-up’ stress (e.g. Hayes 1995), respectively.

In languages with autonomous primary stress, the primary stress behaves independently of and takes precedence over non-primary stresses. The primary-stress alignment or foot type diverges from that of non-primary stresses in a way that disrupts otherwise regular metrical patterning. Huariapano (Panoan, Peru; Parker 1994, 1998), illustrates a pattern of this type.³ In Huariapano, primary stress appears on the final syllable if it has a coda, otherwise on the penultimate syllable, as in (3a). Secondary stresses, in contrast, are insensitive to syllable structure, alternating by syllable regardless of the presence of a coda, as in (3b).

Primary and secondary stresses in Huariapano exhibit an asymmetry in their quantity sensitivity. The general procedures and/or constraints for assigning stresses, as needed for the forms in (3b), would fail to correctly stress forms such as [hõn.(ˈʦis)] and [ja.(ˈwiʃ)], preferring instead *[(ˈhõn.ʦis)] and *[(ˈja.wiʃ)]. Therefore, there must be primary-stress-specific mandates at work in the language, and they must override those general to all stresses.

In contrast, Cairene Arabic provides a classic example of the second type of asymmetry, which characterises parasitic primary stress. As seen in (4), building left-aligned trochaic feet and assigning primary stress to the rightmost one accounts for the primary stress location (McCarthy 1979).

What makes this pattern different from the others considered so far (Pintupi, Warao and Huariapano) is that stating the primary stress location without referencing the trochaic iteration of metrical foot structure is problematic: the primary stress in the examples above appears on the penultimate or antepenultimate syllable, whichever is an even number of syllables from the beginning of the word. Although this description is technically adequate, it duplicates the normal role of foot structure by referencing a counting mechanism. Moreover, the generalisation is made even more complex when the quantity sensitivity of Cairene Arabic foot structure is taken into account (see §5.1). Although the primary stress obeys its own mandate for alignment (here, being right aligned), this is subordinated to the preferences of the general metrical structure (which here prefers left alignment). Parasitic primary stress, then, arises when the primary stress appears in a location that cannot be soundly described without referencing the metrical structure of a whole prosodic word, not just the edges of that word.

In summary, primary stress may be neutral with respect to non-primary stresses and display a convergent or symmetric relationship. Or the primary and non-primary stresses may diverge in one of two ways, privileging either the mandates of primary stress (autonomous) or those of general metrical structure (parasitic). The next section will leave primary stress briefly to introduce the framework of HS and justify it with some of its results from extant literature. §2.3 will then return to the topic of primary stress typology within a serial framework.

2.2 Serialism in stress

Harmonic Serialism (HS; Prince & Smolensky 2004, McCarthy 2010, 2016) is a serial version of Optimality Theory (OT; Prince & Smolensky 2004). This section begins by briefly summarising the main tenets of HS and surveying its previous results with respect to foot construction and its interactions. The goal is to establish that HS is a viable model of stress assignment, as the serialism of foot-building coincides with empirical findings at a number of levels.

In HS, the grammar models the mapping from a phonological underlying form to a phonological surface form with a series of evaluations against a hierarchy of violable constraints. At each evaluation, the candidate-generation function, Gen, provides a set of candidates from which the ‘winner’ is chosen. By hypothesis, Gen in HS is restricted to making one change at a time, so that candidates differ from the input to that evaluation by the application of, at most, one operation. Because underlying and surface forms often differ in multiple ways, the grammar is iterated, with the winner at each step being an input to another evaluation, where it is compared against another set of one-change candidates provided by Gen. This process continues until no more changes confer an advantage according to the constraint ranking, which is evidenced when the winning candidate at a given step matches the input to that step (referred to as ‘convergence’). The ranking stays the same throughout the derivation. For foundational works in HS that provide a more detailed description of the framework, see especially McCarthy (2000, 2006, 2010, 2016).

What counts as ‘one operation’ for candidate generation in HS is a topic of ongoing research (McCarthy 2009). With respect to stress assignment, there is evidence that metrical feet should be built one at a time (McCarthy 2008b, Kimper 2011, Pruitt 2010, 2012, Topintzi 2016), that metrical structure must interact serially with operations such as epenthesis (Elfner 2016, Moore-Cantwell 2016) and deletion (McCarthy 2008b), and that building metrical structure in a separate step from feature-changing operations prevents several pathological predictions that arise from parallel OT's freedom of analysis (Jesney 2011, Staubs 2013, 2016). I will now review some of these findings.

Pruitt (2010, 2012) argues that serial foot-building is typologically advantageous with standard stress constraints (i.e. the Parse-σ/alignment theory, Prince & Smolensky 2004, McCarthy & Prince 1993a; cf. e.g. Kager 2001, 2005, McCarthy 2003, Hyde 2001, 2016 for alternatives). With these constraints, parallel OT predicts unattested patterns of foot construction that are essentially non-directional (Hyde 2007), but HS successfully avoids this prediction by parsing incrementally with no derivational foresight. Similarly, McCarthy (2008b) and Topintzi (2016) both present analyses of foot construction in specific languages (Awajún and Iquito, respectively) that rely on serial foot construction to correctly control the location of monosyllabic or monomoraic feet.

Elfner (2016) presents analyses of several languages with interactions between stress and epenthesis and argues that the separation of epenthesis and stress assignment into different derivational steps is crucial to an account of the observed typology of both transparent and opaque interactions. With respect to deletion, McCarthy (2008b) uses HS to provide an account of metrically conditioned syncope. The crucial move is for footing and deletion to be in different steps of the derivation.

Jesney (2011) shows that HS can be used to solve a recognised typological gap where positional faithfulness constraints predict the assignment of a privileged position to a less marked segment (rather than functioning as intended just to preserve contrasts in strong positions). Jesney shows that HS correctly predicts that such interactions do not occur, as long as segmental operations occur in a different step from the establishment of the privileged positions with processes such as foot-building.⁴ Work by Staubs (2013, 2016) makes a similar argument with segmental features and positional markedness constraints.

To summarise, there is considerable evidence in the literature that HS should be entertained as a model of phonology, and that HS foot-building is both internally serial (one foot at a time) and separate from other structural and segmental operations. This is not to suggest that each of these results is unassailable. For example, Hyde (2012b) argues against Pruitt's (2010) proposal, and Bowers (2019) suggests that metrically conditioned syncope is not a synchronic process, contra McCarthy (2008b). It is clear that the comparison of parallelism and serialism will continue (see also Adler & Zymet 2021, among others). Nonetheless, the range of work in HS, which extends beyond the summaries given here, does at least prompt us to ask the question of how and when a derivation assigns primary stress.

2.3 The puzzle

Intuitively, the typology of primary stress, as laid out in §2.1, presents a puzzle for a serial theory, which has previously been acknowledged in the context of rule-based approaches (whose solutions are summarised just below). Autonomous primary stress systems (such as Huariapano) are those where the primary stress has properties or obeys restrictions that are different from those of non-primary stresses and where the foot structure seems to then orient around the location of primary stress. Therefore, these languages seem to favour a theory whereby the primary stress is assigned early in a derivation, before non-primary foot construction. In contrast, an attempt to assign primary stress in a language with parasitic primary stress (such as Cairene Arabic) without knowing the location of feet throughout the word would have to grapple directly with a complicated generalisation. Delaying primary-stress assignment until foot construction has occurred accounts for its location in a comparatively straightforward way.

The rule-based (and serial) metrical literature contains a diverse set of proposals for dealing with this typological variation. Some reject, reanalyse or set aside some of the attested patterns so that a primary-stress-first or primary-stress-last theory can be made to work across the board. (For a primary-stress-first approach, see especially van der Hulst 1984 et seq.; for primary-stress-last, see e.g. Hayes 1980, Hammond 1985a,b, Halle & Vergnaud 1987.) The works in the serial rule-based literature that acknowledge a similar range of primary stress patterns usually assume a language-specific ordering solution, either implicitly or explicitly. Hayes (1995: 117–118), for example, proposes that languages are parametrically ‘top-down’ (primary-stress-first) or ‘bottom-up’ (primary-stress-last) (see also Odden 1979, Kager 1989, Goldsmith 1990, Hurch 1996). However, this solution is not available in HS, because constraint-based and rule-based serial approaches differ fundamentally in their access to extrinsic ordering. This will be shown in detail toward the end of the argument, in §5.3.

The primary stress ordering puzzle is sidestepped altogether in parallel OT, of course, where the primary stress can straightforwardly affect and be affected by other metrical structure because all operations are considered in parallel. But if we wish to account for the typology of primary stress while maintaining any of the results of HS, a solution short of full parallelism is needed. The next section proposes such a solution.

3 Proposal: Primary stress parallelism

I assume a bracketed grid representation (Hayes 1995 and precursors cited therein) and follow most work in metrical theory in assuming that primary word stress is the manifestation of headedness at the level of the prosodic word (PWd). Consistent with the work surveyed in §2.2, I assume that the candidate-generation function Gen builds headed feet one at a time.

In a bracketed grid representation, assigning primary stress is equivalent to designating a foot (and, by transitivity, that foot's prominent syllable) as the unique head of the PWd. This is represented as a grid mark at the word level, as illustrated in (5).

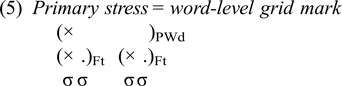
In HS, the puzzle identified in §2.3 manifests in the definition of Gen: what counts as ‘one step’ when it comes to primary-stress assignment or the addition of a word-level grid mark? I propose that the typological facts – the existence of both autonomous and parasitic primary stress patterns – point to just one solution for HS: Gen must treat primary-stress assignment and reassignment as ‘free’, meaning that it occurs in parallel with the application of foot-building processes. This has the following specific corollaries:

1. (6) Primary stress in Gen (proposal):

   1. a. Simultaneity: Primary stress is (and must be) assigned simultaneously with foot construction.

      = A word-level grid mark accompanies the construction of the first foot.

   2. b. Mobility: Primary stress may be reassigned freely with subsequent foot construction.

      = The location of the word-level grid mark is continually (re)evaluated to find its optimal position.

Simultaneity means that a foot is designated as the primary stress at the same derivational step in which it is built, and this entails any primary-stress constraints being active immediately in the selection of the optimal location and shape of the first foot constructed. Therefore, primary-stress constraints may override the preferences of other stress constraints under some rankings. This will permit an analysis of autonomous primary stress systems in HS, as detailed in §4. This has essentially been the assumption of previous work in HS, including McCarthy (2008b), Elfner (2016) and McCarthy et al. (2016). Topintzi (2016), moreover, makes a similar argument with regard to the simultaneity of footing and the formation of a prosodic colon.⁵

Mobility, on the other hand, means that the primary stress is not necessarily fixed in its initial location. As additional feet are constructed, Gen permits candidates in which primary and secondary stress levels are freely exchanged, with the constraint ranking determining whether such candidates better those in which the primary stress remains stationary. The example below makes the representation of mobility explicit. A derivational step at which (ˈσσ)σσσ is input yields candidates that add a foot without shifting primary stress as in (7a), and others that add a foot and shift primary stress to it at the same time as in (7b). Both kinds of candidates are produced by Gen, and either type may be favoured, depending on ranking.

§5 will detail the role of mobility in the analysis of parasitic primary stress systems. In short, mobility solves what would otherwise be an undergeneration problem for HS. Insofar as simultaneity is empirically necessary for autonomous primary stress, there must be an additional mechanism for the analysis of parasitic stress systems, whereby the primary stress is determined with reference to the word's entire metrical structure. §5.3 will show that simply allowing ranking to choose between primary-stress-first and primary-stress-last derivations is not possible in HS. Therefore, mobility is proposed to account for parasitic systems.

Simultaneity and mobility follow from the treatment of the operation of primary-stress assignment as ‘free’ in Gen (but not in Con, where primary stress markedness constraints must exist and exert various pressures to account for the optimal primary stress location in a language, as the analyses in this paper will demonstrate). ‘Free’ operations have some precedent in HS, particularly with respect to syllabification. According to McCarthy (2007, 2009), syllabification may occur without costing a derivational step (i.e. in parallel with other processes). McCarthy (2009) argues that syllabification must be this way so that the consequences of syncope can be realised immediately, and this accounts for the myriad cases in which syncope is blocked when an unsyllabifiable sequence of segments would result.⁶ As §§4–5 will show, the reasons for treating the primary stress operation as free are similar: the location of the primary stress both affects and is affected by the overall metrical structure of a word.⁷

Taken together, simultaneity and mobility mean that the location of primary stress is assessed in parallel with foot-building. However, the building of individual feet and the application of segmental processes remain subject to gradualness or serialism. Therefore, we retain the overall serial architecture of HS and the positive results that derive from it (§2.2). The next sections show detailed evidence for simultaneity (§4) and mobility (§5) with a more in-depth look at case studies of primary stress and a discussion and refutation of possible alternatives to the admission of limited parallelism in HS.

4 Simultaneity

This section begins by revisiting and expanding on the Huariapano data from §2.1 to illustrate and justify simultaneity in primary stress. Other patterns of autonomous primary stress and alternatives to simultaneity in HS are then discussed.

4.1 Case study: Huariapano

Huariapano is a Panoan language formerly spoken in Peru (Parker 1994, 1998). In Huariapano, primary stress is quantity-sensitive and aligned to the right word edge, while secondary stresses are quantity-insensitive and show two patterns of directionality (discussed further below). The dominant primary stress pattern of Huariapano stresses the final syllable if heavy; otherwise, the primary stress surfaces on the penultimate syllable.⁸ Vowel length is not contrastive and appears only in monosyllabic words to satisfy a bimoraic word minimum. Syllables closed by a consonant are heavy, attracting stress in final position, with the exception of a glottal stop, which is not phonemic and does not attract final stress (Parker 1994, 1998). The examples in (8) illustrate this pattern. The words in (8a) end with a light syllable and receive penult stress, while the words in (8b) have a final heavy syllable that receives the primary stress. Huariapano primary stress can be analysed with the moraic trochee as the basic foot type (i.e. (ˈH) or (ˈLL); Hayes 1995), although, considering the available evidence, an alternative that permits an (ˈHL) foot cannot be ruled out. Committing to one or the other is not crucial for our current purposes.

Unlike primary stress, secondary stresses in Huariapano are quantity-insensitive and described by Parker (1998: 7) with syllabic trochees.¹⁰ Parker reports that the secondary stresses may be either right- or left-aligned (that is, iterating right-to-left away from, or left-to-right toward, the primary stress foot), with each root needing to be lexically marked for its direction of secondary stress alignment (Parker 1998: 8). In addition to the longer forms in (8); the data in (9) provide evidence of these patterns; the forms in (9b) show left alignment of secondaries, while the forms in (9c) show right alignment; and the forms in (9a) are consistent with both.

The asymmetry in the sensitivity to quantity exhibited by primary and secondary stresses is the sense in which Huariapano's primary stress can be considered autonomous. The mechanisms that produce secondary stresses cannot be sensitive to syllable weight; therefore, final primary stress would not arise from those dictates alone. Conversely, the quantity sensitivity must be specified to apply to the primary stress foot only, rather than across the board, since a fully quantity-sensitive parse would not arrive at the secondary stress feet in (9). This scenario is straightforwardly accounted for under the current proposal: the candidates for the first foot receive primary stress by default due to simultaneity, and this will invoke primary-stress-specific demands on the foot's placement. Subsequent foot construction is quantity-insensitive, because non-primary stresses are not subject to the primary-stress-specific constraint(s). I assume that constraints may be general to all stresses or unique to primary stress, but there are no constraints that refer specifically to non-primary stresses (McGarrity 2003).

To derive stress patterns in HS, I will adopt the Parse-σ/generalised alignment theory of stress (McCarthy & Prince 1993a, Prince & Smolensky 2004; see Kager 1999 for a summary), with the constraints defined in (10). Although gradient alignment constraints have been criticised in OT stress theory (e.g. McCarthy 2003), Pruitt (2012) defends their use in HS. As Pruitt (2012) demonstrates, the categorical foot alignment constraints proposed by McCarthy (2003) fail to control stress patterns under certain circumstances, and an additional proposed alternative based on *Lapse constraints (Kager 2001, 2005, McCarthy 2003) makes problematic predictions in serial stress derivations (see also Torres-Tamarit & Jurgec 2015).

1. (10)

   1. a. Parse-σ

      Assign a violation mark for every syllable that is not a member of a foot (Prince & Smolensky 2004).

   2. b. Iamb/Trochee

      Assign a violation mark for a foot whose head is not aligned with its right/left edge (Prince & Smolensky 2004).

   3. c. FtBin

      Assign a violation mark for a monomoraic foot; *(ˈL) (Prince & Smolensky 2004).¹¹

   4. d. AllFtR/L

   For each foot in a PWd, assign one violation mark for every syllable separating it from the right/left edge of the PWd (McCarthy & Prince 1993a).

In addition to these basic stress constraints, I will employ AlignHd, as defined in (11), as the primary-stress alignment constraint in this paper. This definition refers to the primary stress syllable and assigns violation marks gradiently according to the degree of misalignment.¹²

1. (11) AlignHdR/L

   Assign a violation mark for each syllable separating the primary stress syllable from the right/left edge of the PWd.

I adopt an analysis of Huariapano which accounts for the quantity sensitivity of the primary stress as emerging from the interaction of AlignHdR, FtBin and Trochee. When the final syllable is heavy, FtBin, Trochee and AlignHdR can be simultaneously satisfied with a final (ˈH) foot. But when the final syllable is light, at least one of these constraints is violated. Huariapano selects (ˈσL) to satisfy FtBin and Trochee, and tolerates minimal violation of AlignHdR. This approach to right-edge primary stress quantity sensitivity is proposed for English by Pater (2000: 241–243), who justifies the approach on typological grounds. As Pater argues, using the primary-stress-specific (and gradient) constraint AlignHdR to analyse such cases accounts for the fact that exceptional primary-stress quantity sensitivity appears to occur only at the right word edge in trochaic languages, whereas exceptional primary stress quantity-insensitivity is restricted to left word edges in trochaic languages. Additionally consistent with this approach is the attestation of mirror-image left-edge primary-stress quantity sensitivity in iambic languages (‘initial if heavy, else peninitial’; Hayes 1995: 261). The tableaux in (12) and (13) show how the Huariapano primary stress pattern is derived with these constraints.¹³

1. (12) Penult stress when final syllable is light

   Step 1 of HS derivation

   

2. (13) Final stress when final syllable is heavy

   Step 1 of HS derivation

The secondary stresses, in contrast, are not subject to AlignHdR, which means that other constraints determine their distribution, resulting in quantity-insensitive trochees in the rest of the word. Parker (1998) proposes that the lexical variation seen in secondary stresses can be handled with root-specific rankings of AllFtL and AllFtR. Both outcomes are illustrated in (14) and (15) below. In each case, the ranking of AlignHdR over both foot alignment constraints ensures that the direction of secondary stress feet may vary without affecting the primary stress foot. Candidates with primary stress mobility (the topic of §5) have been omitted to avoid cluttering the illustration, but it can be verified from tableaux (14) and (15) that the high rank of AlignHdR would successfully rule out any candidate with a different primary stress location.

1. (14) Left-aligned secondary stresses

   Step 2 for /mɯ.raj.βa.ʂi.ki/ ‘we found’

   

2. (15) Right-aligned secondary stresses

   Step 2 for /mi.βom.bi.ra.ma/ ‘you (pl)’

   

This analysis transparently requires simultaneity to work. If, for the sake of illustration, we imagine a bottom-up theory that does not place primary stress on the first foot when it is constructed, then primary-stress-specific constraints (here, AlignHdR) can have no effect on the outcome. The tableau in (16) illustrates this point. The other constraints (Trochee, FtBin, Parse-σ and AllFtL/R) favour quantity-insensitive trochees and, therefore, no additional motivation exists for stress to be placed on the final syllable, even when it is heavy, eventually leading to stress on the wrong syllable.

1. (16) No final stress without simultaneity

   • Step 1

     

   • Step 2

     

     Predicted winner: *[(ˈja.wiʃ)]

There are, of course, constraints that favour stressing heavy syllables in general, such as Weight-to-Stress (Prince 1990). This kind of constraint could be used to select candidate (b) in (16), which would then lead to correct primary stress placement at the second step, [ja.(ˈwiʃ)]. But utilising such a constraint in this case predicts quantity sensitivity across the board in Huariapano, not just in primary stresses, which is counter to fact. Therefore, the constraint that motivates quantity-sensitive behaviour must be specific to primary stress, and must be active at the first foot-building step, which means simultaneity is required.

An alternative analysis of Huariapano can be found in the work of Bennett (2012, 2013), where several aspects of Parker's description and metrical interpretation are challenged. Most relevant for the present discussion is that Bennett's account of the quantity asymmetry in Huariapano assumes that final codas are moraic but that medial codas never are, an anti-extrametricality effect. Under this alternative, all parsing in Huariapano is technically quantity-sensitive, and the grammar controls the potential distribution of quantity separately. Therefore, the exceptional quantity sensitivity of the primary stress is a by-product of two orthogonal features: right-aligned primary stress and word-final (but not word-medial) weight-by-position. Instead of varying in quantity sensitivity, as I have assumed here, this alternative sees the primary and secondary stress feet of Huariapano as varying in directionality only. A further element of Bennett's proposal is that secondary stresses are always left-aligned but may be iambic or trochaic, depending on the root. Bennett's reanalysis is motivated by the distribution of epenthetic [h], which is rhythmic but not correlated with the foot structure that Parker (1998) proposes for stress (and that I have followed in my analysis).

If exceptional right-edge quantity sensitivity is handled in the way Bennett suggests, Huariapano's primary stress would not present evidence for simultaneity, since the quantity sensitivity of the final stress would be correlated only coincidentally with the fact that it is the primary stress, and thus, no primary-stress-specific constraints would be needed (Bennett 2013: 382). On the other hand, quantity asymmetries between primary and non-primary stresses are fairly robustly attested to (e.g. McGarrity 2003, Goedemans & van der Hulst 2014), and Bennett's account of the Huariapano asymmetry would not extend to all of them. In English, for example, nouns and suffixed adjectives tend to show stress on the penultimate syllable if it is heavy; otherwise, it falls to the antepenultimate syllable. This is the rather common ‘Latin stress rule’ (see e.g. Hayes 1995: 91–92, 180–181), and it is identical to Huariapano's primary stress generalisation except for the exclusion of the final syllable from the calculation. Yet, like Huariapano, English has non-primary stress feet that obey different generalisations with respect to quantity and, therefore, show an asymmetry (e.g. Halle & Vergnaud 1987, Pater 2000). Primary stress sacrifices parsing in favour of quantity sensitivity (or better right alignment), e.g. ho(rí)zon, not *(hóri)zon (Pater 2000: 240, 249). But secondary stresses are quantity-sensitive only when it is consistent with maximal parsing. Pater (2000: 247) gives the example of a peninitial heavy syllable that is stressed in (Tìm)(bùc)(tóo), but not in (Àlex)(án)der, *A(lèx)(án)der.

The extrametricality of the final syllable in English means that final syllable weight by-position (Bennett's analysis of Huariapano) cannot capture these asymmetries, and a primary-stress-specific constraint is needed instead. Given its independent motivation, then, an interpretation of Huariapano that correlates quantity sensitivity with primary vs. non-primary stress – as I have done here, following Parker's descriptions – is not anomalous, despite the availability of a potential alternative analysis.

To summarise, Huariapano constitutes an example of autonomous primary stress and, therefore, evidence for primary stress simultaneity, under an interpretation of the data where the quantity asymmetry is fundamentally derived from the primary/secondary stress distinction rather than being arbitrarily coincident with the location of primary stress. This asymmetry implies that primary and non-primary stresses obey partially distinct rankings, and I have analysed the quantity sensitivity of primary stress to be an effect of AlignHdR, following Pater (2000). For primary-stress constraints to affect foot-building in HS, the designation of primary stress must be simultaneous with the construction of feet. Otherwise, general stress constraints would rule in favour of quantity-insensitive parsing, as required to govern the distribution of secondary stresses.

4.2 Other patterns

Huariapano and English are not alone in showing a fundamental asymmetry between primary and non-primary stresses. For example, Inga, a Quechuan language of Colombia, is described by Levinsohn (1976: 29) as having a pattern very similar to Huariapano: when the final syllable is closed by a sonorant consonant, primary stress is final; otherwise, it is penultimate, and secondary stresses are reported to appear optionally in a leftward alternation from the primary stress. The asymmetry can also go the other way, where primary stress is quantity-insensitive due to edge alignment requirements while non-primaries are quantity-sensitive (McGarrity 2003). Furthermore, a considerable body of literature has amassed discussing other ways that primary and non-primary stresses can differ from one another in the same language. Relatively extensive discussions of such asymmetries appear in Odden (1979), Hurch (1996), McGarrity (2003), and Goedemans & van der Hulst (2014). These sources note that primary and non-primary stresses often require distinct generalisations, and, according to this literature, just about any dimension of metrical description can be the locus of such differences, including directionality, quantity sensitivity, extrametricality and foot type.

Not all such asymmetries are evidence for simultaneity. As Pruitt (2019) shows, it is possible to achieve a ‘bottom-up’ analysis of an asymmetry (i.e. without simultaneity) when there is evidence that a well-motivated general (not primary-stress-specific) stress constraint can create two distinct patterns among stresses before primary stress is assigned. Simultaneity, then, is really motivated by typological patterns rather than individual languages: it boils down to a question of whether the nature of the asymmetry is, cross-linguistically, unique to the primary/non-primary distinction. While it is not possible to vet every attested primary/non-primary-stress asymmetry for evidence of simultaneity in this paper, it would seem from the previous literature on the topic that there are a sufficient number of such cases to support the existence of autonomous primary stress. Moreover, allusions to similar arguments have been made previously in the literature, usually contrasting fully parallel OT with rule-based metrical theory. For example, Prince & Smolensky's (2004) argument for parallelism in the analysis of Latin stress is, when viewed closely, an argument for simultaneity (see e.g. Prince & Smolensky 2004: 70).¹⁴ Because the stress asymmetries behind autonomous primary stress are multidimensional and diverse, the most straightforward solution is to allow constraints specific to primary stress to affect foot-building, which is accomplished with simultaneity.

4.3 Potential alternatives to simultaneity in HS

Before moving on, I will briefly address two imaginable HS alternatives to simultaneity; that is, ways of deriving autonomous primary stress that do not require the first foot to bear primary stress immediately. First, Gen could in principle be defined to produce derivations as in (17), using Huaripano as an example. A non-primary stress foot is built at step 1, it receives primary stress at step 2, at which point the primary-stress constraints become active and favour moving the foot to a more harmonic location at step 3.

1. (17) Derivation of Huariapano with foot movement

   /ja.wiʃ/ → (ˌja.wiʃ) → (ˈja.wiʃ) → ja.(ˈwiʃ) → [ja.(ˈwiʃ)]

But there are challenges inherent in this approach to autonomous primary stress. One is that it conflicts with previous literature. Under the proposal of Elfner (2016), for example, this derivation would be impossible, as changing or moving a foot in any way requires separate steps in which the foot is removed and then rebuilt. Moreover, primary-stress autonomy manifests in a number of different ways, so implementing this alternative would require a fully articulated theory of foot movement with a great deal of flexibility that was capable of accounting for cases where a foot must move a long distance and/or occupy a different kind of foot once it is assigned primary stress. The predictions of a theory with liberal foot-changing or foot-movement operations would, in turn, have to be carefully scrutinised to ensure the benefits of incremental parsing are retained (see, e.g. McCarthy & Pruitt 2013: 122). For these reasons, foot movement does not seem to be a better alternative than simply permitting primary stress simultaneity.

A final alternative to simultaneity would be to implement the strictly ‘top-down’ treatment of primary stress adopted in some rule-based theories, where primary-stress assignment occurs by designating a prominent syllable at the word level without simultaneously building a foot, making it more or less non-metrical. This approach can be found in the work of Hayes (1995), where it is an optional ordering, and van der Hulst (1997, 2009, 2012, 2014), where it is required (see also Hurch 1996). In the theory of Hayes, foot construction follows at a later derivational step, and a foot head is ensured ‘under’ the primary stress by the Continuous Column Constraint (1995: 34). In the theory of van der Hulst, primary stress is accentual rather than culminative and is wholly separate from rhythmic non-primary stresses; thus a foot is neither needed nor assumed.

There are two potential problems with imagining the non-metrical approach in HS. First, if we assume with Hayes (1995) that word-level stress involves a bracketed grid representation, then placing a word-level grid mark before foot construction requires that the Continuous Column Constraint be violable. Although the theory of Hayes (1995) permits temporary violation of the constraint, it otherwise functions as an undominated filter on subsequent foot-building so that no surface forms incur a violation. But this is not possible in HS. Although HS does permit derivations where surface-unviolated constraints are temporarily violated at intermediate steps (as discussed explicitly by McCarthy et al. 2016, for example), it is not generally possible to ensure that derivations converge with a given violable constraint satisfied under every ranking. If the Continuous Column Constraint is treated as violable in general, then it is likely that under some rankings, a violation of the constraint will persist to the surface. (Some related discussion appears in §5.3.) The theory of van der Hulst (1997 et seq.) circumvents this issue, because a metrical grid is not assumed; the primary stress is treated as accentual and, therefore, no lower-level structure is needed to support it. But this version of non-metrical ‘top-down’ primary stress encounters a second challenge, as the variety of ways primary stress manifests requires an articulated theory of primary stress placement that partially duplicates the usual role of feet (e.g. by proposing that primary stress is normally assigned in a two-syllable window at the word edge). My proposal assumes instead that feet are the vehicle for stress assignment, but that simultaneity allows for both general and primary-stress-specific constraints to negotiate its appropriate shape and location.

4.4 Summary

This section has demonstrated the need for simultaneity in primary stress, with the grammar being able to designate a foot as the primary stress when it is built. Without such an option, all feet will be treated the same in the course of parsing, but in some languages the primary stress foot can appear in a location or with characteristics that are not consistent with the generalisations about non-primary stress in the language. To borrow a phrase from Bailey (1995: ii), in these languages, primary stress is not a matter of ‘secondary stress plus something extra’; instead, it obeys autonomous principles. In OT, this suggests that primary stress is subject to different or additional constraints, a relatively uncontroversial hypothesis. However, as this section has shown, it is also necessary to adopt a definition of GEN that permits those constraints to actively affect foot-building, just as simultaneity does. The next section turns to parasitic primary stress systems, where the primary stress can be identified only with reference to non-primary stress, and shows how mobility is crucial for their analysis.

5 Mobility

This section turns to Cairene Arabic as a case study in parasitic primary stress and provides an illustration of how the current proposal – HS with primary-stress mobility – accounts for this pattern. Further examples of parasitic primary stress are reviewed, and an alternative to primary-stress mobility is considered and rejected.

5.1 Case study: Cairene Arabic

Example (18) shows the Cairene Arabic stress pattern, repeating and adding to the data that were presented in §2.1. These data illustrate the pronunciation of Classical Arabic words in the dialect of speakers educated in Cairo, as originally presented by Mitchell (1975). The Cairene dialect of Arabic shows quantity-sensitive trochaic parsing (CVC and CVː are heavy) with a prohibition on final stress except when the final syllable is superheavy (CVCC or CVːC). When the final syllable is not superheavy, the stress pattern is as follows: stress the penult if it is heavy, as in (18a), but when the penult is light, stress either the penult (18b) or the antepenult (18c), whichever is an even number of syllables away from the rightmost non-final heavy syllable or the beginning of the word.¹⁵

As this description suggests, determining the location of primary stress in Cairene Arabic appears to require counting syllables, but McCarthy (1979) shows that the pattern is naturally described by positing left-to-right, quantity-sensitive foot construction and primary stress on the rightmost foot.¹⁶ Clearly, these data are a problem if one assumes that the main stress is always correctly located at the beginning of the stress derivation (as it was in Huariapano, for example). Therefore, the analysis proposed here invokes primary-stress mobility: the primary stress may move freely to another foot as the derivation progresses. Its final location is determined by the ranking of primary-stress-specific constraints.

For Cairene, the general pattern for feet is left-aligned trochees, which is achieved with Trochee, Parse-σ ≫ AllFtL ≫ AllFtR. The primary stress ends up on the rightmost foot, not the leftmost, so AlignHdR must dominate its opposite, AlignHdL. However, to prevent AlignHdR from affecting the location of the first foot, it must itself be dominated by AllFtL. The first iteration is shown with the most relevant constraints in (19). We will also need constraints that govern the quantity sensitivity of feet, but I have chosen a word with only light syllables in (19)–(21) to illustrate the basic analysis of parasitic primary stress in HS and set aside the grammar's representation of quantity sensitivity.

1. (19) Left-aligned first foot in Cairene Arabic

   Step 1

   

At the second step, the candidate set will include two candidates for every possible way of building a foot: one that adds a foot and does not move primary stress at the same time, and one that adds a foot and does move the primary stress. As shown in (20), because AllFtL dominates AllFtR and AlignHdR, the next foot built will be left-aligned like the previous one. But because shifting the primary stress to the new foot is permitted by Gen and because AlignHdR dominates AlignHdL, the optimal candidate is (d), the one that adds the left-aligned trochee and shifts the primary stress onto it.

1. (20) Mobility of primary stress as parsing proceeds

   Step 2

   

At the third step the derivation converges on [(ˌʃa.ʤa)(ˈra.tu).hu], as shown in (21), because adding a word-final stress with a monosyllabic foot violates both FtBin and NonFinality. Both constraints must be high-ranked in Cairene Arabic – NonFinality is violated only when the final syllable is superheavy, and FtBin is never violated – so either one could be used to rule out candidates (b) and (c) in (21). Although candidate (c), which shifts stress further to the right, maximally satisfies AlignHdR, its violations of FtBin and NonFinality are fatal, so antepenultimate primary stress is optimal.

1. (21) Not optimal to parse final syllable

   Step 3 (Convergence)

   

Within the current proposal, then, parasitic primary-stress systems can be analysed successfully in HS by permitting mobility. As the metrical structure of a word is built, an optimal position for primary stress within that structure can be selected by continuing to evaluate possible primary-stress locations throughout the derivation.

5.2 Other patterns

Unlike autonomous primary stress, which manifests in different ways for different languages, parasitic primary-stress systems are generally similar. They can be diagnosed with the following criterion: primary stress is assigned near one edge of the word, but exactly which syllable it is assigned to is determined by the number of syllables separating it in the opposite direction from the word edge or another landmark (such as a heavy syllable in the case of Cairene Arabic). In addition to Cairene Arabic, Hayes (1995: 36) lists Seminole/Creek, Wargamay, Munsee/Unami, Malecite-Passamaquoddy and Eastern Ojibwa as languages that have this characteristic. Additional examples include Nyawaygi, which is reported to have a stress pattern identical to neighbouring Wargamay (Dixon 1983); MalakMalak (Birk 1976, Goldsmith 1990), whose stress pattern is similar to Wargamay and Nyawaygi; and Asheninca, which has left-aligned secondary stresses with primary stress appearing on a rightmost foot (Pichis Ashéninka: Payne 1990; Ajyíninka Apurucayali: Payne et al. 1982, McCarthy & Prince 1993b).

The following descriptions from the literature are similar in obvious ways to the description of Cairene above and are typical of parasitic primary-stress systems.

1. (22) Wargamay (Pama-Nyungan, Australia; Dixon 1981: 20)

Stress is assigned as follows:

1. (1) If the first syllable involves a long vowel, then it must receive primary stress.

2. (2) If there is no long vowel in a word, and (a) the word is disyllabic or quadrisyllabic, primary stress goes on the first syllable, (b) the word is trisyllabic or quinquesyllabic, primary stress goes on the second syllable.

Secondary stress goes on the syllable next but one after primary stress, except that a final syllable can never bear stress.

1. (23) Creek (Muskogean, Oklahoma; Haas 1977: 202–3)

In any string of L[ight] syllables containing no fixed accent, the tonal accent will be placed on the last even-numbered syllable. In other words, if the total number of syllables in the word is odd, the tonal accent is on the penult, but if the total number is even, the tonal accent is on the ultima […]

Furthermore, if there is a string of L[ight] syllables following a H[eavy] syllable, the rule of placing the tonal accent on the last even-numbered L[ight] syllable will apply.

Although context-free descriptions (that is, descriptions which do not reference metrical structure) of the primary-stress location in such languages invariably sound non-local, metrical theory permits analyses where the word is parsed iteratively into foot structure and the primary stress assigned at the ‘end’ of the directional parse, as we have seen for Cairene Arabic (McCarthy 1979, Halle & Vergnaud 1987: 58 ff.). The analysis of Cairene can be extended to the other parasitic primary-stress languages with the necessary adjustments in ranking for different foot types (whether trochaic, iambic, quantity-sensitive or not, etc.) and directionality/alignment. Under the current analysis, the ranking schema shown in (24) is common to all parasitic systems I am aware of.

1. (24) Ranking schema for parasitic primary stress in HS

   AllFt(α) ≫ AlignHd(¬α) ≫ AllFt(¬α), AlignHd(α)

   (where α ∈ {L, R})

As always in OT theories, it is technically possible to invent constraints with exactly the right favouring relations to place primary stress in the correct place in these languages even before the rest of the word's metrical structure is constructed, which would permit an analysis without mobility. An imagined set of constraints would essentially restate the primary-stress generalisation as above. (E.g. ‘Assign a violation mark for a primary stress that is not an even number of syllables to the right of a heavy syllable or the beginning of the word.’) But simply hard-coding the generalisation into constraints with disjunctive violation criteria and/or references to syllable parity is clearly not an insightful way to capture the generalisations in such languages. Moreover, the typological predictions of such constraints would be highly suspect.

Therefore, I conclude that a primary-stress-first derivation requires mobility to analyse parasitic primary-stress languages. Short of presenting evidence that such languages have been mischaracterised, there is no better analysis than allowing the primary stress to be placed among feet rather than independent of them, which I have proposed to achieve through the free movement of the primary stress as the derivation progresses.

5.3 The failure of parametric approaches in HS

This paper has argued thus far that primary stress must be assigned at the first step of foot-building to account for languages with autonomous primary stress, while parasitic primary-stress systems nonetheless have an optimal primary-stress location that cannot be determined until later in the derivation. To reconcile these requirements, I have proposed that while primary-stress assignment is obligatorily simultaneous with foot-building, it can be moved at later derivational steps to a different location (if favoured by the ranking of primary-stress constraints). However, a conceivable alternative to this state of affairs is an approach akin to that of Hayes (1995) and some others in the rule-based literature, where both primary-stress-first (‘top-down’) and primary-stress-last (‘bottom-up’) derivations are possible and the choice between them is determined on a language-particular basis (i.e. parametrically). The intuition is that if primary-stress assignment can be delayed for a bottom-up analysis of parasitic systems, mobility would not be necessary. I will show in this section that parametric ordering of this sort cannot be successfully modelled in HS.

The simplest version of the parametric approach would be to treat the assignment of primary stress as optional, rather than obligatory, at step 1 of footing. Autonomous primary-stress languages would be those where simultaneous primary-stress assignment is optimal at step 1, while parasitic languages would arise under rankings that prefer delaying primary-stress assignment. This approach fails right out of the gate, however, because it cannot reliably analyse parasitic systems. Briefly, if constraints are ranked to disprefer primary stress at the first iteration of stress assignment, they will in many circumstances continue to disprefer primary stress, converging on outputs with foot structure but no primary stress (Pruitt 2012).

A more promising (though ultimately still unsuccessful) parametric approach is suggested by an anonymous reviewer. This approach capitalises on the connection between prosodic wordhood and primary stress, proposing that autonomous and parasitic languages differ in the order of foot-building and PWd formation. In autonomous primary-stress languages, ranking favours early PWd-building, as the derivation in (25a) shows, while parasitic primary-stress languages favour parsing words into feet first, with PWd formation and primary-stress assignment occurring once no more parsing is possible, as in (25b).

The derivation of Cairene Arabic under this hypothesis is shown in (26). The constraint WdCon motivates parsing lexical words into prosodic words. Prosodic word formation is marked with curly braces {…}.

1. (26) Cairene Arabic with delayed PWd formation

   • Step 1

     

   • Step 2

     

   • Step 3

     

However, this alternative fails as a general solution for two reasons. First, the constraints responsible for motivating the existence of feet and their location routinely make reference to PWd boundaries. Alignment constraints such as AllFtL/R, for example, assign violation marks for feet according to their (mis)alignment relative to PWd edges (McCarthy & Prince 1993a). Without a PWd, therefore, it is not clear how the constraint could behave as intended.

Even if we could redefine stress constraints to motivate footing in the absence of PWds, however, this alternative would face a second challenge. As the step 3 tableau in (26) reveals, the ranking WdCon ≫ AlignHdR is crucial to the analysis of Cairene Arabic, because building a PWd and assigning primary stress along with it will inevitably introduce violations of primary-stress markedness constraints. To achieve culminative derivations, the constraint that favours building PWds must always rank above any primary-stress markedness constraints that will be violated. But since this cannot be guaranteed in factorial typology, we predict two problematic types of languages: (i) those where no words of the language achieve PWd status because primary-stress constraints that cannot be perfectly satisfied rank too highly (e.g. a version of Cairene Arabic with AlignHdR ≫ WdCon), and (ii) those where only a subset of words with arbitrary properties are PWds because the dominant primary-stress constraints can be satisfied for some inputs but not others (non-uniform PWd formation; Pruitt 2012). In a language with right-to-left trochees, for example, AlignHdL could be perfectly satisfied only in words with an even number of syllables. If AlignHdL ≫ WdCon, we predict a language where even-parity lexical words are parsed as PWds, while odd-parity lexical words are not (though they are footed).

To summarise, parametric ordering of footing and primary-stress assignment is a problem in HS, because it requires primary-stress assignment to be non-optimal in the early stages of the derivation for parasitic systems. To put it simply, if primary-stress-motivating constraints are violable, then under some rankings they will be violated, not only by intermediate forms but also by surface forms. And this means predicting languages that do not prosodify at higher levels or do so only for some words and not others. This dovetails with the formally similar argument against the non-metrical approach to primary-stress-first derivations in §4.2: there, it was noted that non-metrical primary stress requires a violable Continuous Column Constraint, predicting that some derivations will converge with violations on the surface. In this respect, the same is true of culminativity in general. Unless certain conditions are met, any structural requirement that can be violated within a derivation is also predicted to be violable in some languages on the surface.¹⁷

In addition to demonstrating that parallelism is crucial to capturing the typology of primary stress in HS, the failure of the parametric ordering approach illuminates a fundamental difference between rule-based phonologies and HS. While ranking does provide HS with a mechanism for favouring different orders of processing, its capacity to model arbitrary ordering is considerably more limited than that of extrinsically ordered rules, because processes apply only when they are optimal according to the constraint ranking (i.e. derivations must be harmonically-improving, McCarthy 2009, 2010), and the ranking stays the same throughout the derivation. In rule theories with extrinsic ordering, culminativity can be ensured by constraints that are effectively violable derivation internally yet inviolable in output forms. But since HS makes no distinction among violabilities at different stages of a derivation, the same mechanisms cannot be summoned. Therefore, inviolable structural requirements must be given a different analysis, which obligatory simultaneity achieves for culminativity. And when simultaneity is obligatory, mobility is likewise required.

5.4 Summary

Parasitic primary-stress systems have long played a role in the construction of metrical theories, and it is clear why: they show a pattern where the primary stress cannot be treated as an autonomous entity, apart from the metrical structure of a word, and instead must be analysed as the culmination of the metrical structure itself. Given the results of §4, which motivated primary-stress simultaneity, this section has proposed that primary-stress mobility must be allowed to account for parasitic systems. We have also seen that alternatives to mobility in HS are unsuccessful at capturing the full range of patterns in a restrictive way, further supporting the notion that primary stress requires parallelism, even in HS, due to its typological diversity.

6 The exceptional parallelism of primary stress

This section presents two final points of discussion. §6.1 considers to what extent the introduction of simultaneity and mobility into HS merges its predictions with that of fully parallel OT. §6.2 pivots to a final point in need of illumination: that of primary-stress uniqueness relative to the rest of the prosodic hierarchy in which it is embedded.

6.1 Full vs. limited parallelism

This paper has discussed the typological variation that exists in primary stress, arguing that primary stress is a cross-linguistically heterogeneous property. For HS to account for the attested variation, primary stress must be assigned simultaneously with initial foot-building and be iteratively reassessed throughout the derivation to find its optimal position. This means that primary stress is permitted to be effectively ‘bottom-up’ and ‘top-down’ at the same time – a hallmark of parallelism. We should now ask whether and how HS with limited parallelism differs from parallel OT, with its full parallelism at all levels.

Simultaneity in HS means that the candidate set for the first iteration of footing includes candidates with one primary-stress foot and candidates with one instance of any other (e.g. segmental) change. Therefore, foot-building is still internally serial and separate from the application of other processes. Likewise, foot-building and other processes remain serialised at subsequent iterations, even when the primary stress is freely moveable. In contrast, parallel OT candidate sets include those available at each HS iteration plus candidates with multiple feet, those with multiple other changes, and those with any and all combinations of the above. Extant arguments for the advantages for HS over parallel OT, some of which were reviewed in §2.2, are all retained under the current proposal, because they rest on the differences that remain between parallel OT and HS, even when simultaneity and mobility of primary stress are admitted.

In principle, a more thorough comparison can be done with available computational tools for calculating factorial typologies, though doing so on a large scale is outside of the scope of this paper. To provide a miniature proof of concept, I computed the predictions of parallel OT and HS with simultaneity and mobility for six- and seven-syllable inputs using the constraints Parse-σ, FtBin, AllFtL/R, Trochee, Iamb and AlignHdL/R. To produce the HS typology, I used OT-Help 2.0 (Staubs et al. 2010), which generates candidates and violations dynamically based on input files that define the operations and constraints with (modified) regular expressions (see Mullin et al. 2010). To produce the parallel OT typology, I used OTWorkplace (Prince & Tesar 2010) to generate the full metrical candidate set for inputs up to seven syllables and then trimmed the file to just six- and seven-syllable inputs (which yielded 958 and 3137 candidates, respectively). I then used a function built into a post-release version of OT-Help 2.0 to automate filling in constraint violation marks in the OT tableaux, using the same constraint-definition file that was used for the HS typology. The resulting tableaux with candidates and violations were then submitted to OTSoft (Hayes et al. 2013), which produced the typology.¹⁸

The result was significant, though not total, overlap in the predicted typologies, with 39 stress patterns predicted by both parallel OT and HS, four predicted only by parallel OT, and six more uniquely produced by HS. For comparison, an HS without mobility has less overlap with parallel OT, because it undergenerates by producing no parasitic systems, and an HS with neither simultaneity nor mobility (i.e. a ‘bottom-up’ Gen) has less overlap with parallel OT due to both under- and overgeneration (no autonomous primary-stress cases and many languages with unattested non-uniform culminativity). Here, I focus on the differences between parallel OT and HS.

The six languages unique to HS are all of the same type; namely, bidirectional patterns with an internal (word-medial) monosyllabic foot. That HS predicts this particular kind of pattern, while parallel OT usually does not, has been previously observed and discussed in the literature (Hyde 2009, 2012a, b, Pruitt 2012: 210 ff.), and is a result of incremental parsing rather than simultaneity and mobility of primary stress.¹⁹

The four unique languages produced by parallel OT do, however, reveal a point of difference between HS and parallel OT with respect to primary stress. To take one of these patterns as an illustrative example, parallel OT predicts a language with the stress pattern (ˌσσ)(ˌσσ)(σˈσ) in six-syllable words and (ˌσσ)(ˌσσ)(σˈσ)σ in seven-syllable words. This pattern is like Cairene Arabic (§5.1), except that the last foot of the parse – the primary-stress foot – is an iamb rather than a trochee. This arises from a ranking that prefers left-to-right trochaic parsing in general but will sacrifice trochaicity in the primary-stress foot for better satisfaction of AlignHdR. In HS, this kind of pattern is not predicted, because if AlignHdR is ranked high enough to change a trochee into an iamb, it will do so throughout the word as each new foot is built and (re)assigned primary stress, yielding (σˌσ)(σˌσ)(σˈσ)σ. In a sense, the stress pattern under this ranking in HS would be opaque, where iambs arise as a result of AlignHdR despite the ranking Trochee ≫ Iamb, but on the surface in HS (though not in parallel OT) the pattern is transparently a left-to-right iambic parse. The other three unique-to-parallel-OT languages are of the same kind, but with different foot types, alignment directions, and tolerance for monosyllabic feet.

Among the next steps in this line of research should be to probe this difference (e.g. is it, on balance, indicative of a net advantage to HS, to parallel OT, or to neither?) and to undertake larger-scale comparisons of predictions with a wider range of inputs, operations/candidates and constraints. Although dynamic candidate and violation-mark generation in OT-Help 2.0 makes the prospects for generating large-scale typologies in HS quite promising, the sheer size of candidate sets in parallel OT presents computational challenges that make equivalent factorial typology calculation a non-trivial (though presumably not insurmountable) undertaking.²⁰ For these reasons, pursuing a fuller-scale factorial typology calculation in parallel OT sufficient to make comparison with HS possible is no doubt an excellent topic for future work.

To summarise the results of this section, primary-stress simultaneity and mobility can be implemented in HS to account for primary-stress typology without disturbing the results of extant literature on HS's advantages over parallel OT, which rely on the serialisation of foot-building in general and in relation to other processes. The typology calculation presented here, moreover, suggests that while HS with simultaneity and mobility brings the predictions of HS closer to that of parallel OT for primary stress specifically, some differences remain, which should be considered carefully in future work.

6.2 Why primary stress is different

I now turn to a question that takes the consideration of primary-stress behaviour outside the theory-based questions that have been the subject of the paper up to this point. One of the implications of the current proposal is a divergence between the characteristics of the foot and word levels of the prosodic hierarchy. I have proposed that word headedness has freedom that feet and foot headedness do not, in the form of mobility or primary-stress reassignment. This begs the question: why should these two levels receive different treatment? Put differently, from what principles does it follow that word and foot headedness diverge in this way? Although I will not provide a formal answer to this question (e.g. by proposing different representations for headedness at the foot and word levels), I will present evidence in this section that suggests the divergence is not merely a convenient proposal for addressing the typological facts presented in this paper but instead reflects a fundamental asymmetry in these levels.

I begin with the observation that non-uniform behaviour among different subparts of the prosodic hierarchy has been noted by previous scholars. Ito & Mester (2003), for example, argue for non-uniformity in the Strict Layer Hypothesis (the principle dictating strict succession and proper containment of prosodic category n−1 within prosodic category n; Selkirk 1984). In particular, they argue that strict succession of prosodic categories is violated at word level, which permits both foot and (crucially) syllable constituents to be daughters. However, they suggest that strict succession is maintained at the foot level, which can dominate only syllabic nodes, never morae directly. In addition, Inkelas (1989: 47–49) proposes that the sub-hierarchy of foot/syllable/mora be excised from the prosodic hierarchy altogether, forming a distinct ‘metrical hierarchy’. The metrical hierarchy relates only indirectly to the prosodic hierarchy proper, through the application of phonological rules responsible for building metrical structure, which apply within prosodic domains. Metrical theory has also generally coalesced around the idea that foot structure is preferentially binary, whereas word structure is (usually) considered n-ary, or essentially flat, where all feet (and unparsed syllables) are grouped together in the same word-level constituent (e.g. Hayes 1995: 119). The frequency with which the word level of the prosodic hierarchy witnesses a departure from the levels below it suggests a separation of the formal characteristics among prosodic levels at precisely the same location as proposed here; namely, that the word level is special relative to those below it. Therefore, it is unsurprising to find that headedness at this level is also special.

There are, moreover, a number of processes that renegotiate headedness at higher levels of prosodic structure without affecting the constituency at lower levels.²¹ The Rhythm Rule in English and other languages, as well as cyclic effects in the stress of morphologically complex words, are prominent examples (e.g. Chomsky & Halle 1968, Liberman & Prince 1977, Kiparsky 1979, among many others). Phrasal stress has generally similar properties: various factors influence the relative strength of heads of a phrase from among options made available by the lower levels of structure (e.g. Hayes 1995: ch. 9).

Diachronic evidence provides indirect support for the thesis that primary stress is treated differently from foot structure. In the histories of a number of languages, it is reported that primary and secondary stresses have ‘exchange[d] relative values’ (Hyman 1977: 75, note 28)). Hyman cites Yanyuwa (‘Anyula’), Warlpiri (‘Wailbri’), and possibly Proto-Celtic to Welsh and Breton. Hurch (1996: 87) notes a similar change in West Slavic. Under the assumption that language change follows a period of synchronic variation, this suggests a stage where the primary stress could have fluctuated among available foot heads while the remaining metrical structure stayed in place. (Trammel 1971: 138 presents a possible example.)

Finally, it can be noted that previous literature has adjudicated on the issue of within-foot headedness in HS and determined that it should not be treated as free in the same way that primary stress is treated here. For example, one of Pruitt's (2010) arguments for deriving stress in HS crucially depends on the absence of free foot-head movement operations (see Pruitt 2010: 512–517). Elfner (2016) goes further and shows that attested opaque stress-epenthesis interactions can be derived in HS only if a shift in foot headedness requires two separate steps.

To summarise, although accounting for the typology of primary stress in HS requires a proposal that fundamentally divides foot- and word-level headedness, evidence from studies of the prosodic hierarchy, synchronic stress shift and diachronic change, as well as from previous work in HS, all suggest that this division is not arbitrary but supported by a range of empirical findings.

7 Conclusion

This paper has argued that the typology of primary stress and its relationship to general metrical structure should be accounted for by positing a specific degree of parallelism – one that encompasses primary-stress simultaneity and mobility – and I have proposed that this degree of parallelism be implemented in HS. On the one hand, these results identify and solve a problem that is specific to HS: how to derive the diverse typology of primary-stress systems serially, when appealing to extrinsic ordering is not possible. On the other hand, the argument has highlighted general issues of both empirical and theoretical importance.

Empirically, this paper noted the existence of primary-stress systems that fall into three categories: autonomous, parasitic, and neutral. While considerable literature has addressed primary-stress diversity, the classifications proposed here have enabled an explicit connection between the language types, the rankings under which they are derived and the degree of parallelism they require. This categorisation of primary-stress systems is, I propose, related to the kind of parallelism they require by definition: autonomous primary-stress systems are those that require simultaneity, and parasitic primary-stress systems are those that require mobility. Neutral primary-stress systems require neither.

From a theoretical standpoint, this paper has contributed comparisons between parallel and serial models on the one hand, and between rule- and constraint-based models on the other. A fundamental difference between rule- and constraint-based theories lies in the availability of arbitrary process ordering. Rule-based theories with extrinsic ordering and inviolable output filters can produce derivations that are not available in HS, where constraints are violable and remain in the same ranking from the beginning to the end of a derivation. The need for limited parallelism in HS is indeed motivated, in part, by the absence of a mechanism for ensuring arbitrary process ordering.

Likewise, the comparison of parallelism and serialism has yielded insights into the nature of process interaction. A central point of this discussion has been that parallelism is not a monolithic, all-or-nothing proposition and should not be treated as such. Rather, when a case for parallelism is made on the basis of some data, it is worth considering what specific degree of parallelism is required and among what processes. In the present case, primary-stress assignment has been argued to invoke parallelism in two ways, yet both are consistent – in theory and in practice – with the proposal that the grammar is otherwise fundamentally serial.

Finally, the findings reported in this paper – evidence for parallelism against a backdrop of serialism – force the conclusion that primary stress is different. Yet, when the totality of extant evidence regarding primary stress is examined, this conclusion is not anomalous. Instead, it weaves together many disparate findings, pointing the way toward further refinement of our understanding of phonological structure by recognising areas of heterogeneity.