Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-26T02:37:00.286Z Has data issue: false hasContentIssue false
  • English
  • Français

Who Should Be Afraid of the Jeffreys-Lindley Paradox?

Published online by Cambridge University Press:  01 January 2022

Aris Spanos
Get access Rights & Permissions [Opens in a new window]

Abstract

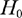The article revisits the large n (sample size) problem as it relates to the Jeffreys-Lindley paradox to compare the frequentist, Bayesian, and likelihoodist approaches to inference and evidence. It is argued that what is fallacious is to interpret a rejection of as providing the same evidence for a particular alternative 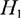, irrespective of n; this is an example of the fallacy of rejection. Moreover, the Bayesian and likelihoodist approaches are shown to be susceptible to the fallacy of acceptance. The key difference is that in frequentist testing the severity evaluation circumvents both fallacies but no such principled remedy exists for the other approaches.

Type
Research Article
Information
Philosophy of Science , Volume 80 , Issue 1 , January 2013 , pp. 73 - 93
Copyright
Copyright © The Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Thanks are due to Deborah Mayo for numerous discussions on these topics and to two anonymous referees for many useful comments and suggestions.

References

Berger, James O. 1985. Statistical Decision Theory and Bayesian Analysis. 2nd ed. New York: Springer.CrossRefGoogle Scholar
Berger, James O. 2003. “Could Fisher, Jeffreys, and Neyman Have Agreed on Testing?” Statistical Science 18 (1): 1–32.CrossRefGoogle Scholar
Berger, James O., Boukai, Ben, and Wang, Yinping. 1997. “Unified Frequentist and Bayesian Testing of Precise Hypotheses.” Statistical Science 12 (3): 133–60.CrossRefGoogle Scholar
Berger, James O., and Delampady, Mohan. 1987. “Testing Precise Hypotheses.” Statistical Science 2 (3): 317–35.Google Scholar
Berger, James O., and Sellke, Thomas. 1987. “Testing a Point Null Hypothesis: The Irreconcilability of P Values and Evidence.” Journal of the American Statistical Association 82 (397): 112–22.Google Scholar
Berger, James O., and Wolpert, Robert W.. 1988. The Likelihood Principle. Lecture Notes, Monograph Series, 2nd ed, vol. 6. Hayward, CA: Institute of Mathematical Statistics.Google Scholar
Casella, George, and Berger, Roger L.. 1987. “Reconciling Bayesian and Frequentist Evidence in the One-Sided Testing Problem.” Journal of the American Statistical Association 82 (397): 106–11.CrossRefGoogle Scholar
Cox, David R., and Hinkley, David V.. 1974. Theoretical Statistics. London: Chapman & Hall.CrossRefGoogle Scholar
Freeman, P. R. 1993. “The Role of P-Values in Analyzing Trial Results.” Statistics in Medicine 12:1433–59.CrossRefGoogle Scholar
Ghosh, Jayanta K., Delampady, Mohan, and Samanta, Tapas. 2006. An Introduction to Bayesian Analysis: Theory and Methods. New York: Springer.Google Scholar
Hacking, Ian. 1965. Logic of Statistical Inference. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Hacking, Ian 1972. Review of Likelihood: An Account of the Statistical Concept of Likelihood and Its Application to Scientific Inference, by A. F. Edwards. British Journal for the Philosophy of Science 23:132–37.Google Scholar
Howson, Colin. 2002. “Bayesianism in Statistics.” In Bayes’s Theorem, ed. Swinburne, R., 39–71. Oxford: Oxford University Press.Google Scholar
Howson, Colin, and Urbach, Peter. 2006. Scientific Reasoning: A Bayesian Approach. 3rd ed. Chicago: Open Court.Google Scholar
Jeffreys, Harold. 1939/1961. Theory of Probability. Oxford: Oxford University Press.Google Scholar
Lehmann, Erich L. 1986. Testing Statistical Hypotheses. 2nd ed. New York: Wiley.CrossRefGoogle Scholar
Lindley, Dennis V. 1957. “A Statistical Paradox.” Biometrika 44:187–92.CrossRefGoogle Scholar
Mayo, Deborah G. 1996. Error and the Growth of Experimental Knowledge. Chicago: University of Chicago Press.CrossRefGoogle Scholar
Mayo, Deborah G., and Spanos, Aris. 2004. “Methodology in Practice: Statistical Misspecification Testing.” Philosophy of Science 71:1007–25.CrossRefGoogle Scholar
Mayo, Deborah G., and Spanos, Aris 2006. “Severe Testing as a Basic Concept in a Neyman-Pearson Philosophy of Induction.” British Journal for the Philosophy of Science 57:323–57.CrossRefGoogle Scholar
Mayo, Deborah G., and Spanos, Aris 2011. “Error Statistics” In Philosophy of Statistics, Handbook of Philosophy of Science, ed. Gabbay, D., Thagard, P., and Woods, J., 153–98. Burlington: Elsevier.Google Scholar
Robert, Christian. 2007. The Bayesian Choice. 2nd ed. New York: Springer.Google Scholar
Royall, Richard M. 1997. Statistical Evidence: A Likelihood Paradigm. London: Chapman & Hall.Google Scholar
Sellke, Thomas, Bayarri, M. J., and Berger, James O.. 2001. “Calibration of P-Values for Testing Precise Null Hypotheses.” American Statistician 55:62–71.CrossRefGoogle Scholar
Shafer, Glenn. 1982. “Lindley’s Paradox.” Journal of the American Statistical Association 77:325–34.Google Scholar
Sober, Elliott. 2008. Evidence and Evolution: The Logic behind the Science. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Spanos, Aris. 2010. “Is Frequentist Testing Vulnerable to the Base-Rate Fallacy?” Philosophy of Science 77:565–83.CrossRefGoogle Scholar
Spanos, Aris 2011. “Misplaced Criticisms of Neyman-Pearson (N-P) Testing in the Case of Two Simple Hypotheses.” Advances and Applications in Statistical Science 6:229–42.Google Scholar
Stone, Mervyn. 1997. “Discussion of Aitkin (1997).” Statistics and Computing 7:263–64.CrossRefGoogle Scholar