Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Finkelstein, L.
and
Leaning, M.S.
1984.
A review of the fundamental concepts of measurement.
Measurement,
Vol. 2,
Issue. 1,
p.
25.
Iverson, G.
and
Falmagne, J.-C.
1985.
Statistical issues in measurement.
Mathematical Social Sciences,
Vol. 10,
Issue. 2,
p.
131.
Heyer, Dieter
and
Niederée, Reinhard
1989.
Mathematical Psychology in Progress.
p.
99.
1989.
Foundations of Measurement.
p.
459.
Goldstein, William M
and
Busemeyer, Jerome R
1992.
The effect of “irrelevant” variables on decision making: Criterion shifts in preferential choice?.
Organizational Behavior and Human Decision Processes,
Vol. 52,
Issue. 3,
p.
425.
Heyer, Dieter
and
Niederée, Reinhard
1992.
Generalizing the concept of binary choice systems induced by rankings: one way of probabilizing deterministic measurement structures.
Mathematical Social Sciences,
Vol. 23,
Issue. 1,
p.
31.
Luce, R. Duncan
and
Narens, Louis
1994.
Patrick Suppes: Scientific Philosopher.
p.
219.
Michelini, R.C.
and
Rossi, G.B.
1995.
Measurement uncertainty: A probabilistic theory for intensive entities.
Measurement,
Vol. 15,
Issue. 3,
p.
143.
Suck, Reinhard
1997.
Probabilistic Biclassification and Random Variable Representations.
Journal of Mathematical Psychology,
Vol. 41,
Issue. 1,
p.
57.
Iverson, Geoffrey
and
Luce, R. Duncan
1998.
Measurement, Judgment and Decision Making.
p.
1.
Heyer, D.
and
Niederée, R.
2001.
International Encyclopedia of the Social & Behavioral Sciences.
p.
9454.
Suck, Reinhard
2001.
The Normal Distribution Derived from Qualitative Conditions.
Journal of Mathematical Psychology,
Vol. 45,
Issue. 2,
p.
370.
Regenwetter, M.
and
Marley, A.A.J.
2001.
Random Relations, Random Utilities, and Random Functions.
Journal of Mathematical Psychology,
Vol. 45,
Issue. 6,
p.
864.
Rossi, Giovanni B.
2003.
A probabilistic model for measurement processes.
Measurement,
Vol. 34,
Issue. 2,
p.
85.
Duncan Luce, R.
2005.
An open measurement problem of interest.
Journal of Mathematical Psychology,
Vol. 49,
Issue. 6,
p.
440.
Rossi, Giovanni Battista
2006.
A probabilistic theory of measurement.
Measurement,
Vol. 39,
Issue. 1,
p.
34.
Suppes, Patrick
2009.
Philosophy of Technology and Engineering Sciences.
p.
825.
Rossi, Giovanni B.
2009.
Data Modeling for Metrology and Testing in Measurement Science.
p.
1.
Rossi, Giovanni Battista
2012.
Toward an Interdisciplinary Probabilistic Theory of Measurement.
IEEE Transactions on Instrumentation and Measurement,
Vol. 61,
Issue. 8,
p.
2095.
Rossi, Giovanni Battista
and
Crenna, Francesco
2013.
Probability as a logic for measurement representations.
Journal of Physics: Conference Series,
Vol. 459,
Issue. ,
p.
012005.
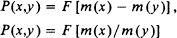 with
with