Research Article
The Numerical Simulation of Space-Time Variable Fractional Order Diffusion Equation
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 571-585
-
- Article
- Export citation
A Fourier Companion Matrix (Multiplication Matrix) with Real-Valued Elements: Finding the Roots of a Trigonometric Polynomial by Matrix Eigensolving
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 586-599
-
- Article
- Export citation
A Hybrid Immersed Interface Method for Driven Stokes Flow in an Elastic Tube
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 600-616-
-
- Article
- Export citation
An h-Adaptive Runge-Kutta Discontinuous Galerkin Method for Hamilton-Jacobi Equations
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 617-636
-
- Article
- Export citation
Error Estimates and Superconvergence of RT0 Mixed Methods for a Class of Semilinear Elliptic Optimal Control Problems
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 637-656
-
- Article
- Export citation
Extremal Eigenvalues of the Sturm-Liouville Problems with Discontinuous Coefficients
-
- Published online by Cambridge University Press:
- 28 May 2015, pp. 657-684
-
- Article
- Export citation

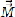 is a multiplication matrix in the sense that, after first defining a vector
is a multiplication matrix in the sense that, after first defining a vector  whose elements are the first 2
whose elements are the first 2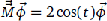 . This relationship is the eigenproblem; the zeros
. This relationship is the eigenproblem; the zeros