Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T13:11:01.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Extrapolation of Mixed Finite Element Approximations for the Maxwell Eigenvalue Problem

Published online by Cambridge University Press:  28 May 2015

Changhui Yao  and
Zhonghua Qiao
Changhui Yao*
Affiliation:
Department of Mathematics, Zhengzhou University, Zhengzhou, China
Zhonghua Qiao
Affiliation:
Institute for Computational Mathematics & Department of Mathematics, Hong Kong Baptist University, Kowloon Tong, Hong Kong
*
Corresponding author.Email address:[email protected]
Get access

Abstract

In this paper, a general method to derive asymptotic error expansion formulas for the mixed finite element approximations of the Maxwell eigenvalue problem is established. Abstract lemmas for the error of the eigenvalue approximations are obtained. Based on the asymptotic error expansion formulas, the Richardson extrapolation method is employed to improve the accuracy of the approximations for the eigenvalues of the Maxwell system from 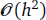to 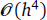when applying the lowest order Nédélec mixed finite element and a nonconforming mixed finite element. To our best knowledge, this is the first superconvergence result of the Maxwell eigenvalue problem by the extrapolation of the mixed finite element approximation. Numerical experiments are provided to demonstrate the theoretical results.

Keywords

65M1065N30Maxwell eigenvalue problemmixed finite elementasymptotic error expansionRichardson extrapolation
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 4 , Issue 3 , August 2011 , pp. 379 - 395
Copyright
Copyright © Global Science Press Limited 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arbenz, P. and Geus, R., Multilevel preconditioned iterative eigensolvers for Maxwell eigenvalue problems, Appl. Numer. Math., 54 (2005), pp. 107–121.CrossRefGoogle Scholar
[2]Arbenz, P., Geus, R., and Stefan Adam, On solving Maxwell eigenvalue problems for accelerating cavities, Phys. Rev. ST Accel. Beams, 4 (2000), pp. 022001.CrossRefGoogle Scholar
[3]Boffi, D., Fernandes, P., Gastaldi, L., and Perugia, I., Computational models of electromagnetic resonators: analysis of edge element approximation, SIAM J. Numer. Anal., 36 (1999), pp. 1264–1290.CrossRefGoogle Scholar
[4]Boffi, D., Finite elements for the time harmonic Maxwell’s equations, In Computational electromagnetics (Kiel, 2001), Vol. 28 of Lect. Notes Comput. Sci. Eng., pp. 11–22, Springer, Berlin, 2003.Google Scholar
[5]Boffi, D., Kikuchi, F., and Schöberl, J., Edge element computation of Maxwell’s eigenvalues on general quadrilateral meshes, Math. Models Methods Appl.Sci., 16 (2006), pp. 265–273.CrossRefGoogle Scholar
[6]Bramble, J. H., Kolev, T. V., and Pasciak, J. E., The approximation of the Maxwell eigenvalue problem using a least-squares method, Math. Comp., 74 (2005), pp. 1575–1598.CrossRefGoogle Scholar
[7]Bramble, J. H. and Pasciak, J. E., A new approximation technique for div-curl systems, Math. Comp., 73 (2004), pp. 1739–1762.CrossRefGoogle Scholar
[8]Caorsi, S., Fernandes, P., and Raffetto, M., On the convergence of Galerkin finite element approximations of electromagnetic eigenproblems, SIAM J. Numer. Anal., 38 (2000), pp. 580–607.CrossRefGoogle Scholar
[9]Chen, W. and Lin, Q.. Asymptotic expansion and extrapolation for the eigenvalue approximation of the biharmonic eigenvalue problem by Ciarlet-Raviart scheme, Adv. Comput. Math., 27 (2007), pp. 95–106.CrossRefGoogle Scholar
[10]Costabel, M. and Dauge, M., Weighted regularization of Maxwell equations in polyhedral domains. A rehabilitation of nodal finite elements, Numer. Math., 93 (2002), pp. 239–277.CrossRefGoogle Scholar
[11]Demkowicz, L., Monk, P., Schwab, C., and Vardapetyan, L., Maxwell eigenvalues and discrete compactness in two dimensions, Comput. Math. Appl., 40 (2000), pp. 589–605.CrossRefGoogle Scholar
[12]Douglas Jr, J.., Santos, J. E., and Sheen, D., A nonconforming mixed finite element method for Maxwell’s equations, Math. Models Methods Appl. Sci., 10 (2000), pp. 593–613.CrossRefGoogle Scholar
[13]Douglas Jr, J.., Santos, J. E., and Sheen, D., A nonconforming mixed method for the time-harmonic Maxwell equations, In Mathematical and numerical aspects of wave propagation (Santiago de Compostela, 2000), pp. 792–796, SIAM, Philadelphia, PA, 2000.Google Scholar
[14]Duan, H. Y., Jia, F., Lin, P, and Tan, R. C. E., The local L2 projected C0 finite element method for Maxwell problem, SIAM J. Numer. Anal., 47 (2009), pp. 1274–1303.CrossRefGoogle Scholar
[15]Hamelinck, W., On the influence of numerical integration on mixedfinite element approximations of a Maxwell eigenvalue problem, J. Comput. Appl. Math., 223 (2009), pp. 929–937.CrossRefGoogle Scholar
[16]Hiptmair, R., Finite elements in computational electromagnetism, Acta Numer., 11 (2002), pp. 237–339.CrossRefGoogle Scholar
[17]Jia, S., Xie, H., Yin, X., and Gao, S., Approximation and eigenvalue extrapolation ofbiharmonic eigenvalue problem by nonconforming finite element methods, Numer. Methods Partial Differential Equations, 24 (2008), pp. 435–448.CrossRefGoogle Scholar
[18]Jia, S., Xie, H., Yin, X., and Gao, S., Approximation and eigenvalue extrapolation of Stokes eigenvalue problem by nonconforming finite element methods, Appl. Math., 54 (2009), pp. 1–15.CrossRefGoogle Scholar
[19]Jiang, B., Wu, J., and Povinelli, L. A., The origin of spurious solutions in computational electromagnetics, J. Comput. Phys., 125 (1996), pp. 104–123.CrossRefGoogle Scholar
[20]Kikuchi, F., Mixed and penalty formulations for finite element analysis of an eigenvalue problem in electromagnetism, Comput. Methods Appl. Mech. Engrg., 64 (1987), pp. 509–521.Google Scholar
[21]Kirsch, A. and Monk, P., Afinite element method for approximating electromagnetic scattering from a conducting object, Numer. Math., 92 (2002), pp. 501–534.CrossRefGoogle Scholar
[22]Lin, Q., Huang, H., and Li, Z., New expansions of numerical eigenvalues for -Au = Xpu by nonconforming elements, Math. Comp., 77 (2008), pp. 2061–2084.CrossRefGoogle Scholar
[23]Lin, Q. and Lin, J., Finite Element Methods:Accuracy and Improvement, Science Press, Beijing, 2006.Google Scholar
[24]Lin, Q., Tobiska, L., and Zhou, A., Superconvergence and extrapolation of non-conforming low order finite elements applied to the Poisson equation, IMA J. Numer. Anal., 25 (2005), pp. 160–181.CrossRefGoogle Scholar
[25]Lin, Q. and Xie, H., Asymptotic error expansion and Richardson extrapolation of eigenvalue approximations for second order elliptic problems by the mixedfinite element method, Appl. Numer. Math., 59 (2009), pp. 1884–1893.CrossRefGoogle Scholar
[26]Lin, Q. and Yan, N., Global superconvergence for Maxwell’s equations, Math. Comp., 69 (2000), pp. 159–176.CrossRefGoogle Scholar
[27]Mercier, B., Osborn, J., Rappaz, J., and Raviart, P. A., Eigenvalue approximation by mixed and hybrid methods, Math. Comp., 36 (1981), pp. 427–453.CrossRefGoogle Scholar
[28]Monk, P., A finite element method for approximating the time-harmonic Maxwell equations, Numer. Math., 63 (1992), pp. 243–261.CrossRefGoogle Scholar
[29]Naga, A., Zhang, Z., and Zhou, A., Enhancing eigenvalue approximation by gradient recovery, SIAM J. Sci. Comput., 28 (2006), pp. 1289–1300.CrossRefGoogle Scholar
[30]Nédélec, J. C., Mixedfinite element in 3D in H(div) and H(curl), In Equadiff 6 (Brno, 1985), Vol. 1192 of Lecture Notes in Math., pp. 321–325, Springer, Berlin, 1986.CrossRefGoogle Scholar
[31]Nédélec, J. C., A new family of mixed finite elements in R3, Numer. Math., 50 (1986), pp. 57–81.CrossRefGoogle Scholar
[32]Qiao, Z. and Yao, C., Superconvergence and extrapolation analysis of a nonconforming mixedfinite element approximation for time-harmonic maxwell’s equations, J. Sci. Comput., 46 (2011), pp. 1–19.CrossRefGoogle Scholar
[33]Xie, H., Extrapolation of the Nédélec element for the Maxwell equations by the mixed finite element method, Adv. Comput. Math., 29 (2008), pp. 135–145.CrossRefGoogle Scholar
[34]Yang, Y., An annlysis of the finite element Method for eigenvalue problems, Guizhou People Public Press, GuiZhou, 2004.(In Chinese).Google Scholar
[35]Yin, X., Xie, H., Jia, S., and Gao, S., Asymptotic expansions and extrapolations of eigenvalues for the stokes problem by mixed finite element methods, J. Comput. Appl. Math., 215 (2008), pp. 127–141.CrossRefGoogle Scholar
[36]Zhang, Z. and Naga, A., A new finite element gradient recovery method: superconvergence property, SIAM J. Sci. Comput., 26 (2005), pp. 1192–1213.CrossRefGoogle Scholar
[37]Zhao, J., Analysis of finite element approximation for time-dependent Maxwell problems, Math. Comp., 73 (2004), pp. 1089–1105.CrossRefGoogle Scholar