Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T08:06:13.296Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bases of the Non-Uniform Cubic Spline Space

Published online by Cambridge University Press:  28 May 2015

Jiang Qian ,
Renhong Wang  and
Chongjun Li
Jiang Qian*
Affiliation:
College of Sciences, Hohai University, Nanjing 210098, China
Renhong Wang
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China
Chongjun Li
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China
*
Corresponding author.Email address:[email protected]
Get access

Abstract

In this paper, the dimension of the nonuniform bivariate spline space 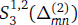is discussed based on the theory of multivariate spline space. Moreover, by means of the Conformality of Smoothing Cofactor Method, the basis of 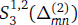composed of two sets of splines are worked out in the form of the values at ten domain points in each triangular cell, both of which possess distinct local supports. Furthermore, the explicit coefficients in terms of B-net are obtained for the two sets of splines respectively.

Keywords

65D07Bivariate splineconformality of smoothing cofactor methodB-netnonuniform type-2 triangulation
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 5 , Issue 4 , November 2012 , pp. 635 - 652
Copyright
Copyright © Global Science Press Limited 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alfeld, P. and Schumaker, L. L., The dimension of bivariate spline spaces of smoothness r for degree d ≥ 4r + 1, Constr. Approx., 3 (1987), pp. 189–197.CrossRefGoogle Scholar
[2]Buhmann, M. D., Radial Basis Functions: Theory and Implementations, Cambridge University Press, 2001.Google Scholar
[3]Dagnino, C. and Lamberti, P., On the approximation power of bivariate quadratic C1 splines, J. Comput. and Appl. Math., 131 (2001), pp. 321–332.CrossRefGoogle Scholar
[4]Dagnino, C. and Lamberti, P., Some performances of local bivariate quadratic C1 quasi-interpolating splines on nonuniform type-2 triangulations, J. Comput. and Appl. Math., 173 (2005), pp. 21–37.CrossRefGoogle Scholar
[5]Deng, J. S., Feng, Y. Y. and Kozak, J., A note on the dimension of the bivariate spline space over the Morgan-Scott triangulation, SIAM J. Numer. Anal., 37(3) (2000), pp. 1021–1028.CrossRefGoogle Scholar
[6]Diener, D., Instability in the dimension of spaces of bivariate piecewise polynomials of degree 2r and smoothness order r, SIAM J. Numer. Anal., 27 (1990), pp. 543–551.CrossRefGoogle Scholar
[7]Dyn, N., Leviatan, D., Levin, D. and Pinkus, A., Multivariate Approximation and Applications, Cambridge University Press, 2001.CrossRefGoogle Scholar
[8]Farin, G., Triangular Bernstein-Bézier, Comput. Aided Geom. Des., 3(2) (1986), pp. 83–127.CrossRefGoogle Scholar
[9]Farin, G., Curves and Surf aces f or Computer Aided Geometric Design, A Practical Guide, Academic Press, Boston, 1992.Google Scholar
[10]Hong, D., Spaces of bivariate spline functions over triangulations, Approx. Theory Appl., 7 (1991), pp. 56–75.Google Scholar
[11]Lamberti, P., Numerical integration based on bivariate quadratic spline quasi-interpolants on bounded domains, BIT Numer. Math., 49 (2009), pp. 565–588.CrossRefGoogle Scholar
[12]Li, C. J. and Wang, R. H., Bivariate cubic spline space and bivariate cubic NURBS surfaces, Proceedings of Geometric Modeling and Processing 2004, IEEE Computer Society Pressvol, pp. 115–123.Google Scholar
[13]Li, C. J. and Chen, J., On the dimensions of bivariate spline spaces and their stability, J. Comput. Appl. Math., 236 (2011), pp. 765–774.CrossRefGoogle Scholar
[14]Liu, H. W., Hong, D. and Cao, D. Q., Bivariate C1 Cubic Spline Space Over a Nonuniform Type-2 Triangulation and its Subspaces with Boundary Conditions, J. Comput. Math. Appl., 49 (2005), pp. 1853–1865.CrossRefGoogle Scholar
[15]Piegl, L. and Tiller, W., The NURBS Book, Spring-Verlag, Berlin, 1997.CrossRefGoogle Scholar
[16]Qian, J. and Y Tang, H., On non-uniform algebraic-hyperbolic (NUAH) B-splines, Numer. Math. A Journal of Chinese Universities, 15(4) (2006), pp. 320–335.Google Scholar
[17]Schumaker, L. L., On the dimension of spaces of piecewise polynomials in two variables, Multivariate Approximation Theory, Schempp, W. and Zeller, K. (Eds.), Birkhauser, Basel, (1979), pp. 396–412.CrossRefGoogle Scholar
[18]Schumaker, L. L., Spline Functions: Basic Theory, Krieger Publishing Company, Malabar FL, 1993.Google Scholar
[19]Shi, X. Q., The singularity of Morgan-Scott triangulation, Comput. Aided Geom. Design, 8 (1991), pp. 201–206.CrossRefGoogle Scholar
[20]Wang, G.J., Wang, G. Z. and Zheng, J. M., Computer Aided Geometric Design, China Higher Education Press/Spring-Verlag Berlin, Beijing/Heidelberg, 2001, (in Chinese).Google Scholar
[21]Wang, G. Z., Chen, Q. Y. and Zhou, M. H., NUATB-spline Curves, Comput. Aided Geom. Design, 21 (2004), pp. 193–205.CrossRefGoogle Scholar
[22]Wang, R. H., The structural characterization and interpolation for multivariate splines, Acta Math. Sinica, 18 (1975), pp. 91–106, (in Chinese).Google Scholar
[23]Wang, R. H., Shi, X. Q., Luo, Z. X. and Su, Z. X., Multivariate Spline Functions and Their Applications, Science Press/Kluwer Academic Publishers, Beijing, New York, Dordrecht, Boston, London, 2001.CrossRefGoogle Scholar
[24]Wang, R. H. and Li, C. J., Bivariate quartic spline spaces and quasi-interpolation operators, J. Comput. Appl. Math., 190 (2006), pp. 325–338.CrossRefGoogle Scholar
[25]Wang, R. H. and Lu, Y, Quasi-interpolating operators and their applications in hypersingular integrals, J. Comput. Math., 16(4) (1998), pp. 337–344.Google Scholar
[26]Wang, R. H. and lu, Y, Quasi-interpolating operators in on non-uniform type-2 triangulations, Numer. Math. A Journal of Chinese Universities, 2 (1999), pp. 97–103.Google Scholar
[27]Wang, S. M., Spline interpolation over type-2 triangulations, Appl. Math. Comput., 49 (1992), pp. 299–313.Google Scholar
[28]Wang, S. M. and Wang, C. L., Smooth interpolation on some triangulations, Utilitas Math., 41 (1992), pp. 309–317.Google Scholar
[29]Xu, Z. Q. and Wang, R. H., The instability degree in the dimension of spaces of bivariate spline, Approx. Theory Appl., 18(1) (2002), pp. 68–80.Google Scholar