Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-18T05:33:26.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Lacunary Interpolation by Fractal Splines with Variable Scaling Parameters

Part of: Approximations and expansions Classical measure theory

Published online by Cambridge University Press:  20 February 2017

P. Viswanathan ,
A.K.B. Chand  and
K.R. Tyada
P. Viswanathan*
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, New Delhi, India
A.K.B. Chand*
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai, India
K.R. Tyada*
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai, India
*
*Corresponding author. Email addresses:[email protected] (P. Viswanathan), [email protected] (A.K.B. Chand), [email protected] (K.R. Tyada)
*Corresponding author. Email addresses:[email protected] (P. Viswanathan), [email protected] (A.K.B. Chand), [email protected] (K.R. Tyada)
*Corresponding author. Email addresses:[email protected] (P. Viswanathan), [email protected] (A.K.B. Chand), [email protected] (K.R. Tyada)
Get access

Abstract

For a prescribed set of lacunary data 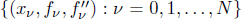with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines 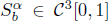satisfying 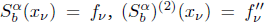for v = 0, 1, … ,N and suitable boundary conditions. To this end, the unique quintic spline introduced by A. Meir and A. Sharma [SIAM J. Numer. Anal. 10(3) 1973, pp. 433-442] is generalized by using fractal functions with variable scaling parameters. The presence of scaling parameters that add extra “degrees of freedom”, self-referentiality of the interpolant, and “fractality” of the third derivative of the interpolant are additional features in the fractal version, which may be advantageous in applications. If the lacunary data is generated from a function Φ satisfying certain smoothness condition, then for suitable choices of scaling factors, the corresponding fractal spline 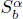satisfies 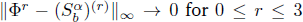, as the number of partition points increases.

Keywords

lacunary interpolationfractal interpolation functionvariable scaling parametersMeir-Sharma quintic splineconvergence

MSC classification

Secondary: 28A80: Fractals 41A05: Interpolation 41A15: Spline approximation 41A25: Rate of convergence, degree of approximation
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 10 , Issue 1 , February 2017 , pp. 65 - 83
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barnsley, M. F., Fractal functions and interpolation, Constr. Approx., vol. 2, (1986), pp. 303–329.CrossRefGoogle Scholar
[2] Barnsley, M. F., Fractals Everywhere, Academic Press, Dublin (1988). (2nd ed., Morgan Kaufmann 1993; 3rd ed., Dover Publications, 2012)Google Scholar
[3] Barnsley, M. F. and Harrington, A. N., The calculus of fractal interpolation functions, J. Approx. Theory, vol. 57 (1989), pp. 14–34.CrossRefGoogle Scholar
[4] Birkhoff, G., Schultz, M.H., and Varga, R.S., Piecewise Hermite interpolation in one and two variables with applications to partial differential equations, Numer. Math., vol. 11 (1968), pp. 232–256.CrossRefGoogle Scholar
[5] Chand, A. K. B. and Navascués, M.A., Generalized Hermite fractal interpolation, Rev Real Academia de Ciencias, Zaragoza, vol. 64 (2009), pp. 107–120.Google Scholar
[6] Dalla, L., Drakopoulos, V., and Prodromou, M., On the box dimension for a class of nonaffine fractal interpolation functions, Analysis in Theory and Appl., vol. 19 (2003), pp. 220–233.CrossRefGoogle Scholar
[7] Karaballi, A. A. and Sallam, S., Lacunary interpolation by quartic splines on uniform meshes, J. Comp. Appl. Math., vol. 80 (1997), pp. 97–104.CrossRefGoogle Scholar
[8] Meir, A. and Sharma, A., Lacunary interpolation by splines, SIAM J. Numer. Anal., vol. 10 (1973), pp. 433–442.CrossRefGoogle Scholar
[9] Navascués, M. A., Fractal approximation, Complex Anal. Oper. Theory, vol. 4 (2010), pp. 953–974.CrossRefGoogle Scholar
[10] Navascués, M. A., Fractal bases of Lp spaces, Fractals, vol. 20 (2012), pp. 141–148.CrossRefGoogle Scholar
[11] Navascués, M. A. and Sebastián, M. V., Smooth fractal interpolation, J. Inequal. Appl., Article ID 78734, (2006), 20 pages.Google Scholar
[12] Schoenberg, I. J., On the Ahlberg-Nilson extension of spline interpolation: The g-splines and their optimal properties, J. Math. Anal. Appl., vol. 21, no. 1, (1968), pp. 207–231.CrossRefGoogle Scholar
[13] Sharma, A., Some poised and nonpoised problems of interpolation, SIAM Review, vol. 14 (1972), pp. 129–151.CrossRefGoogle Scholar
[14] Swartz, B. K. and Varga, R. S., A note on lacunary interpolation by splines, SIAM J. Numer. Anal., vol. 10 (1973), pp. 443–447.CrossRefGoogle Scholar
[15] Viswanathan, P. and Chand, A. K. B., A C1-rational cubic fractal interpolation function: convergence and associated parameter identification problem, Acta Appl. Math., vol. 136 (2015), pp. 19–41.CrossRefGoogle Scholar
[16] Viswanathan, P. and Navascués, M. A., Fractal functions with function scaling factors as solutions of (0, 4) lacunary interpolation problem, Chaos, Solitons, and Fractals, vol. 81 (2015), pp. 98–102.CrossRefGoogle Scholar
[17] Wang, H. Y. and Yu, J. S., Fractal interpolation functions with variable parameters and their analytical properties, J. Approx. Theory, vol. 175 (2013), pp. 1–18.CrossRefGoogle Scholar