Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T13:28:45.026Z Has data issue: false hasContentIssue false
  • English
  • Français

An Unconditionally Stable and High-Order Convergent Difference Scheme for Stokes’ First Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative

Part of: Partial differential equations, initial value and time-dependent initial-boundary value problems Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  20 June 2017

Cuicui Ji  and
Zhizhong Sun
Cuicui Ji
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, P. R. China
Zhizhong Sun*
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, P. R. China
*
*Corresponding author. Email address:[email protected] (Z. Z. Sun)
Get access

Abstract

This article is intended to fill in the blank of the numerical schemes with second-order convergence accuracy in time for nonlinear Stokes’ first problem for a heated generalized second grade fluid with fractional derivative. A linearized difference scheme is proposed. The time fractional-order derivative is discretized by second-order shifted and weighted Gr¨unwald-Letnikov difference operator. The convergence accuracy in space is improved by performing the average operator. The presented numerical method is unconditionally stable with the global convergence order of 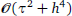in maximum norm, where τ and h are the step sizes in time and space, respectively. Finally, numerical examples are carried out to verify the theoretical results, showing that our scheme is efficient indeed.

Keywords

Stokes’ first problemheat flowfractional derivativefinite difference schemeunconditional stabilityconvergence

MSC classification

Secondary: 65M06: Finite difference methods 65M12: Stability and convergence of numerical methods 65M15: Error bounds 35R11: Fractional partial differential equations
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 10 , Issue 3 , August 2017 , pp. 597 - 613
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Gabriele, A., Spyropoulos, F., and Norton, I. T., Kinetic study of fluid gel formation and viscoelastic response with kappa-carrageenan, Food Hydrocolloid., 23 (2009), pp. 2054–2061.Google Scholar
[2] Tan, W. C. and Masuoka, T., Stokes’ first problem for a second grade fluid in a porous half-space with heated boundary, Int. J. Nonlin. Mech., 40 (2005), pp. 515–522.Google Scholar
[3] Christov, I. C., Stokes’ first problem for some non-newtonian fluids: results and mistakes, Mech. Res. Commun., 37 (2010), pp. 717–723.Google Scholar
[4] Hayat, T., Moitsheki, R. J., and Abelmanc, S., Stokes’ first problem for Sisko fluid over a porous wall, Appl. Math. Comput., 217 (2010), pp. 622–628.Google Scholar
[5] Fetecǎu, C., The Rayleigh-Stokes problem for heated second grade fluids, Int. J. Nonlin. Mech., 37 (2002), pp. 1011–1015.Google Scholar
[6] Abelman, S., Hayat, T. and Momoniat, E., On the Rayleigh problem for a Sisko fluid in a rotating frame, Appl. Math. Comput., 215 (2009), pp. 2515–2520.Google Scholar
[7] Xue, C. F. and Nie, J. X., Exact solutions of Stokes’ first problem for heated generalized Burgers’ fluid in a porous half-space, Nonlinear Anal-Real., 9 (2008), pp. 1628–1637.Google Scholar
[8] Jamil, M., Rauf, A., Zafar, A. A., and Khan, N. A., New exact analytical solutions for Stokes’ first problem of Maxwell fluid with fractional derivative approach, Comput. Math. Appl., 62 (2011), pp. 1013–1023.Google Scholar
[9] Shen, F., Tan, W. C., and Zhao, Y., The Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative model, Nonlinear Anal-Real., 7 (2006), pp. 1072–1080.Google Scholar
[10] Xue, C. F. and Nie, J. X., Exact solutions of the Rayleigh-Stokes problem for a heated generalized second grade fluid in a porous half-space, Appl. Math. Model., 33 (2009), pp. 524–531.Google Scholar
[11] Chen, C. M., Liu, F. and Anh, V., A Fourier method and an extrapolation technique for Stokes’ first problem for a heated generalized second grade fluid with fractional derivative, J. Comput. Appl. Math., 223 (2009), pp. 777–789.Google Scholar
[12] Wu, C. H., Numerical solution for Stokes’ first problem for a heated generalized second grade fluid with fractional derivative, Appl. Numer. Math., 59 (2009), pp. 2571–2583.Google Scholar
[13] Lin, Y. Z. and Jiang, W., Numerical method for stokes’ first problem for a heated generalized second grade fluid with fractional derivative, Numer. Methods Partial Differential Equations., 27 (2011), pp. 1599–1609.Google Scholar
[14] Chen, C. M., Liu, F., Turner, I. and Anh, V., Numerical methods with fourth-order spatial accuracy for variable-order nonlinear Stokes’ first problem for a heated generalized second grade fluid, Comput. Math. Appl., 62 (2011), pp. 971–986.CrossRefGoogle Scholar
[15] Chen, C. M., Liu, F. and Anh, V., Numerical analysis of the Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives, Appl. Math. Comput., 204 (2008), pp. 340–351.Google Scholar
[16] Zhuang, P. H., Liu, Q. X., Numerical method of Rayleigh-Stokes problem for heated generalized second grade fluid with fractional derivative, Appl. Math. Mech. Engl. Ed., 30 (2009), pp. 1533–1546.Google Scholar
[17] Mohebbi, A., Abbaszadeh, M., and Dehghan, M., Compact finite difference scheme and RBF meshless approach for solving 2D Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives, Comput. Method. Appl. M., 264 (2013), pp. 163–177.Google Scholar
[18] Chen, C. M., Liu, F., Burrage, K., and Chen, Y., Numerical methods of the variable-order Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative, IMA J. Appl. Math., 78 (2013), pp. 924–944.Google Scholar
[19] Tian, W., Zhou, H. and Deng, W. H., A class of second order difference approximations for solving space fractional diffusion equations, Math. Comp., 84 (2015), pp. 1703–1727.Google Scholar
[20] Wang, Z. and Vong, S., Compact difference schemes for the modified anomalous fractional subdiffusion equation and the fractional diffusion-wave equation, J. Comput. Phys., 277 (2014), pp. 1–15.Google Scholar
[21] Liao, H. L. and Sun, Z. Z., Maximum norm error bounds of ADI and compact ADI methods for solving parabolic equations, Numer. Meth. Part. D. E., 26 (2010), pp. 37–60.Google Scholar
[22] Sun, Z. Z., Numerical Methods of Partial Differential Equations, 2nd ed., Science Press, Beijing, 2012.Google Scholar
[23] Gao, G. H., Sun, H. W. and Sun, Z. Z., Some high-order difference schemes for the distributed-order differential equations, J. Comput. Phys., 298 (2015), pp. 337–359.Google Scholar
[24] Quarteroni, A. and Valli, A., Numerical Approximation of Partial Differential Equations, Springer, Berlin, 1997.Google Scholar