Published online by Cambridge University Press: 25 January 2022
We study the detection and the reconstruction of a large very dense subgraph in a social graph with n nodes and m edges given as a stream of edges, when the graph follows a power law degree distribution, in the regime when 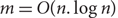 $m=O(n. \log n)$
. A subgraph S is very dense if it has
$m=O(n. \log n)$
. A subgraph S is very dense if it has 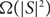 $\Omega(|S|^2)$
edges. We uniformly sample the edges with a Reservoir of size
$\Omega(|S|^2)$
edges. We uniformly sample the edges with a Reservoir of size 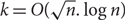 $k=O(\sqrt{n}.\log n)$
. Our detection algorithm checks whether the Reservoir has a giant component. We show that if the graph contains a very dense subgraph of size
$k=O(\sqrt{n}.\log n)$
. Our detection algorithm checks whether the Reservoir has a giant component. We show that if the graph contains a very dense subgraph of size 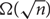 $\Omega(\sqrt{n})$
, then the detection algorithm is almost surely correct. On the other hand, a random graph that follows a power law degree distribution almost surely has no large very dense subgraph, and the detection algorithm is almost surely correct. We define a new model of random graphs which follow a power law degree distribution and have large very dense subgraphs. We then show that on this class of random graphs we can reconstruct a good approximation of the very dense subgraph with high probability. We generalize these results to dynamic graphs defined by sliding windows in a stream of edges.
$\Omega(\sqrt{n})$
, then the detection algorithm is almost surely correct. On the other hand, a random graph that follows a power law degree distribution almost surely has no large very dense subgraph, and the detection algorithm is almost surely correct. We define a new model of random graphs which follow a power law degree distribution and have large very dense subgraphs. We then show that on this class of random graphs we can reconstruct a good approximation of the very dense subgraph with high probability. We generalize these results to dynamic graphs defined by sliding windows in a stream of edges.
Action Editor: Ulrik Brandes
A preliminary version was presented at FODS 2020 (Foundations of Data Science) Conference