Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T12:52:08.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Large very dense subgraphs in a stream of edges

Published online by Cambridge University Press:  25 January 2022

Claire Mathieu  and
Michel de Rougemont Open the ORCID record for Michel de Rougemont [Opens in a new window]
Claire Mathieu
Affiliation:
CNRS and IRIF, Paris, France
Michel de Rougemont*
Affiliation:
University Paris II and IRIF, Paris, France
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the detection and the reconstruction of a large very dense subgraph in a social graph with n nodes and m edges given as a stream of edges, when the graph follows a power law degree distribution, in the regime when 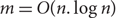$m=O(n. \log n)$ . A subgraph S is very dense if it has 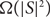$\Omega(|S|^2)$ edges. We uniformly sample the edges with a Reservoir of size 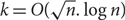$k=O(\sqrt{n}.\log n)$ . Our detection algorithm checks whether the Reservoir has a giant component. We show that if the graph contains a very dense subgraph of size 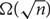$\Omega(\sqrt{n})$ , then the detection algorithm is almost surely correct. On the other hand, a random graph that follows a power law degree distribution almost surely has no large very dense subgraph, and the detection algorithm is almost surely correct. We define a new model of random graphs which follow a power law degree distribution and have large very dense subgraphs. We then show that on this class of random graphs we can reconstruct a good approximation of the very dense subgraph with high probability. We generalize these results to dynamic graphs defined by sliding windows in a stream of edges.

Keywords

dense subgraphsclusteringstreamingprobabilistic analysisrandom graphsapproximation
Type
Research Article
Information
Network Science , Volume 9 , Issue 4 , December 2021 , pp. 403 - 424
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Action Editor: Ulrik Brandes

*

A preliminary version was presented at FODS 2020 (Foundations of Data Science) Conference

References

Aggarwal, C. C., & Wang, H. (2010). Managing and mining graph data (1st ed.). Springer Publishing Company, Incorporated.CrossRefGoogle Scholar
Aiello, W., Chung, F., & Lu, L. (2000). A random graph model for power law graphs. Experimental Mathematics, 10, 53–66.CrossRefGoogle Scholar
Albert, R., & Barabási, A.-L. (2000). Topology of evolving networks: Local events and universality. Physical Review Letters, 85, 5234–5237.10.1103/PhysRevLett.85.5234CrossRefGoogle ScholarPubMed
Babcock, B., Datar, M., & Motwani, R. (2002). Sampling from a moving window over streaming data. In Proceedings of the thirteenth annual ACM-SIAM symposium on discrete algorithms (pp. 633–634). SODA’02.Google Scholar
Bahmani, B., Kumar, R., & Vassilvitskii, S. (2012). Densest subgraph in streaming and mapreduce. Proceedings of the VLDB Endowment, 5(5), 454–465.CrossRefGoogle Scholar
Barabasi, A., & Albert, R. (1999). The emergence of scaling in random networks. Science, 286, 509–512.CrossRefGoogle ScholarPubMed
Bar-Yossef, Z., Jayram, T. S., Kumar, R., & Sivakumar, D. (2004). An information statistics approach to data stream and communication complexity. Journal of Computer and System Sciences, 68(4), 702–732.CrossRefGoogle Scholar
Bhattacharya, S., Henzinger, M., Nanongkai, D., & Tsourakakis, C. E. (2015). Space- and time-efficient algorithm for maintaining dense subgraphs on one-pass dynamic streams. Corr, abs/1504.02268.10.1145/2746539.2746592CrossRefGoogle Scholar
Bollobas, B., Borgs, C., Chayes, J., & Riordan, O. (2010). Percolation on dense graph sequences. The Annals of Probability, 38(1), 150–183.CrossRefGoogle Scholar
Braverman, V., Ostrovsky, R., & Zaniolo, C. (2009). Optimal sampling from sliding windows. In Proceedings of the twenty-eighth ACM SIGMOD-SIGACT-SIGART symposium on principles of database systems (pp. 147–156). PODS’09.CrossRefGoogle Scholar
Chakrabarti, A., Khot, S., & Sun, X. (2003). Near-optimal lower bounds on the multi-party communication complexity of set disjointness. In IEEE conference on computational complexity (pp. 107–117).CrossRefGoogle Scholar
de Rougemont, M., & Vimont, G. (2018). The content correlation of streaming edges. In IEEE international conference on big data (pp. 1101–1106).Google Scholar
Demetrescu, C., Eppstein, D., Galil, Z., & Italiano, G. F. (2010). Dynamic graph algorithms. In Atallah, M. J., & M. Blanton, M. (Eds.), Algorithms and theory of computation handbook.Google Scholar
Ding, J., Lubetzky, E., & Peres, Y. (2014). Anatomy of the giant component: The strictly supercritical regime. European Journal of Combinatorics, 35, 155–168.CrossRefGoogle Scholar
Epasto, A., Lattanzi, S., & Sozio, M. (2015). Efficient densest subgraph computation in evolving graphs. In Proceedings of the 24th international conference on world wide web (pp. 300–310). WWW’15.CrossRefGoogle Scholar
Erdós, P., & Gallai, T. (1960). Gráfok előírt fokszámú pontokkal. Matematikai lapok, 11, 264–274.Google Scholar
Erdös, P., & Renyi, A. (1960). On the evolution of random graphs. Publication of the Mathematical Institute of the Hungarian Academy of Sciences, 17–61.Google Scholar
Esfandiari, H., Hajiaghayi, M., & Woodruff, D. P. (2015). Applications of uniform sampling: Densest subgraph and beyond. Corr, abs/1506.04505.Google Scholar
Hastad, J. (1996). Clique is hard to approximate within n 1−ε. In Proceedings of the 37th annual symposium on foundations of computer science (p. 627). FOCS’96. IEEE Computer Society.CrossRefGoogle Scholar
Khuller, S., & Saha, B. (2009). On finding dense subgraphs. In Proceedings of the 36th international colloquium on automata, languages and programming: Part I (pp. 597–608). ICALP’09.Google Scholar
Kleinberg, J. M., Kumar, R., Raghavan, P., Rajagopalan, S., & Tomkins, A. S. (1999). The web as a graph: Measurements, models, and methods. In Asano, T., H. Imai, D. T. Lee, S.-i. Nakano, & T. Tokuyama (Eds.), Computing and combinatorics (pp. 1–17). Berlin, Heidelberg: Springer.Google Scholar
Kumar, R., Raghavan, P., Rajagopalan, S., Sivakumar, D., Tomkins, A., & Upfal, E. (2000). Stochastic models for the web graph. In Proceedings of the 41st annual symposium on foundations of computer science (p. 57). FOCS’00. IEEE Computer Society.CrossRefGoogle Scholar
Kushilevitz, E, & Nisan, N. (1997). Communication complexity. Cambridge University Press.Google Scholar
Leskovec, J., Kleinberg, J., & Faloutsos, C. (2005). Graphs over time: Densification laws, shrinking diameters and possible explanations. In Proceedings of the eleventh ACM SIGKDD international conference on knowledge discovery in data mining (pp. 177–187). KDD’05.CrossRefGoogle Scholar
McGregor, A., Tench, D., Vorotnikova, S., & Vu, H. T. (2015). Densest subgraph in dynamic graph streams. Corr, abs/1506.04417.CrossRefGoogle Scholar
Molloy, M., & Reed, B. (1998). The size of the giant component of a random graph with a given degree sequence. Combinatorics, Probability and Computing, 7(3), 295–305.CrossRefGoogle Scholar
Moreno, J. L., & Jennings, H. H. (1938). Statistics of social configurations. Jstor, 1(3/4), 342–374.Google Scholar
Newman, M. (2010). Networks: An introduction. Oxford University Press, Inc.CrossRefGoogle Scholar
Newman, M. E. J., Strogatz, S. H., & Watts, D. (2001). Random graphs with arbitrary degree distributions and their applications. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 64(09), 026118.CrossRefGoogle ScholarPubMed
Pittel, B., & Wormald, N. C. (2005). Counting connected graphs inside-out. Journal of Combinatorial Theory, Series B, 93(2), 127–172.CrossRefGoogle Scholar
Vitter, J. S. (1985). Random sampling with a reservoir. ACM Transactions on Mathematical Software, 11(1), 37–57.CrossRefGoogle Scholar
Watts, D. J., & Dodds, P. S. (2007). Influentials, networks, and public opinion formation. Journal of Consumer Research, 34(4), 441–458.CrossRefGoogle Scholar