Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T15:35:50.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak solutions of a quasi-linear degenerate elliptic system with discontinuous coefficients

Published online by Cambridge University Press:  22 January 2016

Yoshiaki Ikeda
Yoshiaki Ikeda*
Affiliation:
Department of Mathematics, Aichi University of Education, Kariya, 448, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall discuss regularities and related topics on weak solutions of the system of the following quasi-linear elliptic differential equations (a combination of almost single equations)

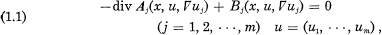
in a bounded domain Ω in Rn (n ≧ 2), where A1j … (A1j …, Anj) are given vector functions of (x, u, ▽uj), Bj are scalar functions of the same variables, and ▽uj = (∂uj/∂x1, …, ∂uj/∂xj denote the gradients of the uj = uj(x) (j = 1, …, m).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 94 , June 1984 , pp. 105 - 135
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1984

References

[ 1 ] Mandras, F., Il problema di Dirichlet per una classe di sistemi lineari non-uniformente ellittici, Rend. Sem. Fac. Sci. Univ. Cagliari, 45 (1975), 333–345.Google Scholar
[ 2 ] Mandras, F., Principio di massimo debole per sotto-soluzioni di sistemi lineari ellittici debolmente accoppiati, Boll. Un. Mat. Ital. (5) 13-A (1976), 592–600.Google Scholar
[ 3 ] Mandras, F., Disegualianza di Harnack per sistemi ellittici debolmente accoppiati, Boll. Un. Mat. Ital. (5) 14-A (1977), 313–321.Google Scholar
[ 4 ] Moser, J., On Harnack’s theorem for elliptic differential equations, Comm. Pure. Appl. Math., 14 (1961), 577–591.Google Scholar
[ 5 ] Murthy, M. K. V. and Stampacchia, G., Boundary value problems for some degenerate-elliptic operators, Ann. Pura. Appl., 80 (1968), 1–122.Google Scholar
[ 6 ] Nirenberg, L., On elliptic differential equationsa, Ann. Scula Norm. Sup. Pisa, 13 (1959), 116–162.Google Scholar
[ 7 ] Serrin, J., Local behavior of solutions of quasi-linear equations, Acta Math., 111 (1964), 247–302.CrossRefGoogle Scholar
[ 8 ] Stampacchia, G., Équations elliptiques du second ordre à coefficients discontinus, Séminaire sur les équations aux dérivées partielles, Collège de France (mai 1964).Google Scholar
[ 9 ] Stampacchia, G., Le problème de Dirichlet pour les équations discontinus, Ann. Inst. Fourier, 15 (1965) 189–258.Google Scholar
[10] Trudinger, N. S., On Harnack type inequalities and their application to quasi-linear elliptic equations, Comm. Pure. Appl. Math., 20 (1967), 721–747. MR 37#1788.Google Scholar
[11] Trudinger, N. S., Linear elliptic operator with measurable coefficients, Ann. Scuola Norm. Sup. Pisa, 27 (1973) 265–308.Google Scholar