Article contents
Vector Field Energies and Critical Metrics on Kähler Manifolds
Published online by Cambridge University Press: 22 January 2016
Abstract
Associated with a Hamiltonian holomorphic vector field on a compact Kähler manifold, a nice functional on a space of Kähler metrics will be constructed as an integration of the bilinear pairing in [FM] contracted with the Hamiltonian holomorphic vector field. As applications, we have functionals 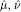 whose critical points are extremal Kähler metrics or “Kähler-Einstein metrics” in the sense of [M4], respectively. Finally, the same method as used by [G1] allows us to obtain, from the convexity of
whose critical points are extremal Kähler metrics or “Kähler-Einstein metrics” in the sense of [M4], respectively. Finally, the same method as used by [G1] allows us to obtain, from the convexity of 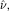 , the uniqueness of “Kähler-Einstein metrics” on nonsingular toric Fano varieties possibly with nonvanishing Futaki character.
, the uniqueness of “Kähler-Einstein metrics” on nonsingular toric Fano varieties possibly with nonvanishing Futaki character.
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 2001
References
- 5
- Cited by


