Article contents
The uniqueness of positive solutions of parabolic equations of divergence form on an unbounded domain
Published online by Cambridge University Press: 22 January 2016
Extract
Let Rn+1 = Rn × R be the (n + 1)-dimensional Euclidean space (n ≥ 1). For X ∈ Rn+1, we write X = (x, t) with x ∈ Rn and t ∈ R. We consider parabolic operators of the following form:
(1) 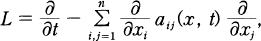
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1993
References
- 2
- Cited by


