No CrossRef data available.
Published online by Cambridge University Press: 22 January 2016
Die Struktur diskret bewerteter perfekter Körper ist bisher von H. Hasse, F. K. Schmidt, O. Teichmüller und E, Witt eingehend untersucht worden. Es ist schon von diesen Autoren bewiesen worden, dass der Restklassenkörper 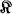 eines diskret perfekten Körpers K stets in K ein mit
eines diskret perfekten Körpers K stets in K ein mit 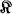 multiplikativ isomorphes Repräsentantensystem besitzt, und sogar, dass es im charakteristikgleichen Fall ein Reprasentantensystem R von
multiplikativ isomorphes Repräsentantensystem besitzt, und sogar, dass es im charakteristikgleichen Fall ein Reprasentantensystem R von 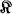 gibt, welches einen mit
gibt, welches einen mit 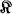 isomorphen Körper bildet. Dabei lässt sich K ais Potenzreihenkörper eines Primelementes aus K mit Koeffizienten aus R darstellen.
isomorphen Körper bildet. Dabei lässt sich K ais Potenzreihenkörper eines Primelementes aus K mit Koeffizienten aus R darstellen.
1) Hasse, H. und Schmidt, F. K., Die Struktur diskret bewerteter Körper, Journ. f. reine u. angew. Math., 170 (1934).Google Scholar
Teichmüller, O., Über die Struktur diskret bewerteter perfekter Körper, Gött. Nachrichten, N.F. 1 (1936).Google Scholar
Teichmüller, O., Diskret bewertete perfekte Körper mit unvollkommenem Restklassenkörper, Journ. f. reine u. angew. Math., 176 (1937).Google Scholar
Witt, E., Zyklische Körper und Algebren der Charakteristik p vom Grade pn , Journ. f. reine u. angew. Math., 176 (1937).Google Scholar
2) Für die allgemeine Theorie der Bewertung siehe das Buch von V. d. Waerden; Moderne Algebra, I. (1937), X. Kapt. Bewerteter Körper.
3) Für y = 0 setzen wir in üblicher Weise w(0)=∞
4) Dabei ist θ0 = t gesetzt.