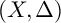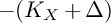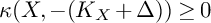1 Introduction
Let
![]() $(X, \Delta )$
be a klt pair with nef log-canonical divisor
$(X, \Delta )$
be a klt pair with nef log-canonical divisor
![]() $K_X + \Delta $
. Recall that the celebrated Non-Vanishing conjecture predicts that
$K_X + \Delta $
. Recall that the celebrated Non-Vanishing conjecture predicts that
![]() $\kappa (X, K_X + \Delta ) \geq 0$
, i.e. that there exists an integer
$\kappa (X, K_X + \Delta ) \geq 0$
, i.e. that there exists an integer
![]() $m\geq 1$
such that
$m\geq 1$
such that
![]() $m(K_X + \Delta )$
is Cartier and
$m(K_X + \Delta )$
is Cartier and
Along with the Abundance conjecture, which predicts that
![]() $K_X + \Delta $
is even semiample, the Non-Vanishing conjecture has attracted much attention. One might be tempted to ponder what happens on the opposite end of the spectrum, namely, when the anti-log canonical divisor
$K_X + \Delta $
is even semiample, the Non-Vanishing conjecture has attracted much attention. One might be tempted to ponder what happens on the opposite end of the spectrum, namely, when the anti-log canonical divisor
![]() $-(K_X + \Delta )$
is nef. One quickly realises that the situation is somewhat different: Already the example of
$-(K_X + \Delta )$
is nef. One quickly realises that the situation is somewhat different: Already the example of
![]() $\operatorname {{\mathbb {P}}}^2$
blown-up in
$\operatorname {{\mathbb {P}}}^2$
blown-up in
![]() $9$
points shows that
$9$
points shows that
![]() $-K_X$
might be nef but fail to be semiample, see [Reference Koike17]. On the other hand, in [Reference Bauer and Peternell1] the authors classified rather explicitly smooth projective threefolds with nef anti-canonical class and observed a posteriori that
$-K_X$
might be nef but fail to be semiample, see [Reference Koike17]. On the other hand, in [Reference Bauer and Peternell1] the authors classified rather explicitly smooth projective threefolds with nef anti-canonical class and observed a posteriori that
![]() $\kappa (X, -K_X)\geq 0$
, at least when X is rationally connected, see also [Reference Xie31] and [Reference Xie32].
$\kappa (X, -K_X)\geq 0$
, at least when X is rationally connected, see also [Reference Xie31] and [Reference Xie32].
Recently, Lazić–Matsumura–Peternell–Tsakanikas–Xie [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21] studied varieties with nef anticanonical bundle with a view towards the recently proposed generalised Non-Vanishing conjecture [Reference Lazić and Peternell20], [Reference Han and Liu14]. In particular, they proved that
![]() $\kappa (X, -(K_X+\Delta ))\geq 0$
if
$\kappa (X, -(K_X+\Delta ))\geq 0$
if
![]() $(X, \Delta )$
is a rationally connected threefold pair with nef anti-log canonical bundle and they asked whether the same conclusion holds more generally, assuming only that
$(X, \Delta )$
is a rationally connected threefold pair with nef anti-log canonical bundle and they asked whether the same conclusion holds more generally, assuming only that
![]() $-(K_X + \Delta )$
is nef. In this paper, we want to give the following affirmative answer to this question:
$-(K_X + \Delta )$
is nef. In this paper, we want to give the following affirmative answer to this question:
Theorem A. Let
![]() $(X, \Delta )$
be a projective klt pair and assume that the anti-log canonical divisor
$(X, \Delta )$
be a projective klt pair and assume that the anti-log canonical divisor
![]() $-(K_X + \Delta )$
is nef. Let
$-(K_X + \Delta )$
is nef. Let
![]() $(F, \Delta _F)$
denote a general fibre of the MRC-fibration of X. If
$(F, \Delta _F)$
denote a general fibre of the MRC-fibration of X. If
![]() $-(K_F + \Delta _F)$
is semiample, then
$-(K_F + \Delta _F)$
is semiample, then
Despite giving only a partial answer, Theorem A applies in many cases. For example, as can be seen by using [Reference Hausen and Süß15], it applies whenever F is a surface with enough automorphisms. Thus, combining our result with [Reference Han and Liu14] and [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21] to deal with the other cases enables us to fully settle the three-dimensional case:
Corollary B. Let
![]() $(X, \Delta )$
be a projective klt threefold pair such that
$(X, \Delta )$
be a projective klt threefold pair such that
![]() $-(K_X + \Delta )$
is nef. Then
$-(K_X + \Delta )$
is nef. Then
Besides the results obtained in [Reference Cao and Höring9] and [Reference Matsumura and Wang23], which form the backbone of our strategy, the main ingredient in our proof of Theorem A is the following “equivariant Non-Vanishing theorem,” which allows us to lift sections from F to X as explained in Section 2. It holds in greater generality and might be of independent interest:
Theorem C (Equivariant Non-Vanishing for Anti-Canonical Divisors).
Let
![]() $(X, D)$
be a projective sub-log canonical pair and assume that
$(X, D)$
be a projective sub-log canonical pair and assume that
![]() $-(K_X + D)$
is semiample. Then for any commutative, linear algebraic subgroup
$-(K_X + D)$
is semiample. Then for any commutative, linear algebraic subgroup
![]() $H\subseteq \operatorname {\mathrm {Aut}}(X, D)$
there exists an integer
$H\subseteq \operatorname {\mathrm {Aut}}(X, D)$
there exists an integer
![]() $m\geq 1$
such that
$m\geq 1$
such that
![]() $-m(K_X + D)$
is Cartier and
$-m(K_X + D)$
is Cartier and
We will abbreviate this by writing
![]() $\kappa (X, -(K_X + D))^H\geq 0$
.
$\kappa (X, -(K_X + D))^H\geq 0$
.
Here,
![]() $\operatorname {\mathrm {Aut}}(X, D)\subseteq \operatorname {\mathrm {Aut}}(X)$
denotes the subgroup of automorphisms
$\operatorname {\mathrm {Aut}}(X, D)\subseteq \operatorname {\mathrm {Aut}}(X)$
denotes the subgroup of automorphisms
![]() $\varphi \in \operatorname {\mathrm {Aut}}(X)$
leaving D invariant as a subset of X. Then
$\varphi \in \operatorname {\mathrm {Aut}}(X)$
leaving D invariant as a subset of X. Then
![]() $\operatorname {\mathrm {Aut}}(X, D)$
acts on
$\operatorname {\mathrm {Aut}}(X, D)$
acts on
![]() $H^0(X, \mathcal {O}_X(-m(K_X + D))\big ))$
in a natural way and we denote by
$H^0(X, \mathcal {O}_X(-m(K_X + D))\big ))$
in a natural way and we denote by
![]() $H^0(X, \mathcal {O}_X({-}m(K_X + D)))^H $
the space of sections which are fixed under this action. For our terminology concerning pairs we refer the reader to Section 1.2 below.
$H^0(X, \mathcal {O}_X({-}m(K_X + D)))^H $
the space of sections which are fixed under this action. For our terminology concerning pairs we refer the reader to Section 1.2 below.
We would like to emphasise that the conclusion of Theorem C is astonishing to the author in several different ways: First, perhaps somewhat unexpectedly, the crucial assumption in Theorem C is the log canonicity and not the semipositivity of
![]() $-(K_X + D)$
, as the conclusion of Theorem C can fail even if
$-(K_X + D)$
, as the conclusion of Theorem C can fail even if
![]() $(X, D)$
is log smooth and if
$(X, D)$
is log smooth and if
![]() $-(K_X + D)$
is ample as soon as
$-(K_X + D)$
is ample as soon as
![]() $(X, D)$
is no longer sub-log canonical, see Example 3.24.
$(X, D)$
is no longer sub-log canonical, see Example 3.24.
Moreover, it is noteworthy that the action of H on the space of sections of
![]() $-m(K_X+D)$
is usually far from being trivial and already in very simple examples the ring of invariant sections of
$-m(K_X+D)$
is usually far from being trivial and already in very simple examples the ring of invariant sections of
![]() $-(K_X + D)$
might be much smaller than the ring of all sections, cf. Example 3.23. Nevertheless, Theorem C shows that there always do exist invariant sections. In particular, in case
$-(K_X + D)$
might be much smaller than the ring of all sections, cf. Example 3.23. Nevertheless, Theorem C shows that there always do exist invariant sections. In particular, in case
![]() $\kappa (X, -(K_X + D)) = 0$
the action must be trivial after all.
$\kappa (X, -(K_X + D)) = 0$
the action must be trivial after all.
Finally, note that the conclusion of Theorem C certainly fails if one allows for more general subgroups of
![]() $\operatorname {\mathrm {Aut}}(X, D)$
, cf. Example 3.22.
$\operatorname {\mathrm {Aut}}(X, D)$
, cf. Example 3.22.
1.1 Overview of the methods used in the proof of Theorem C
By far the most important special case of Theorem C is the one where
![]() $(X, D)$
is log smooth and
$(X, D)$
is log smooth and
![]() $H \cong (\operatorname {{\mathbb {C}}}^{\times })^r$
is an algebraic torus. Indeed, the general case is readily reduced to this one; the precise argument is contained in Section 4.
$H \cong (\operatorname {{\mathbb {C}}}^{\times })^r$
is an algebraic torus. Indeed, the general case is readily reduced to this one; the precise argument is contained in Section 4.
Under these assumptions, the main idea of the proof is to convert the global question of whether
![]() $\kappa (X, -(K_X + D))^{H}\geq 0$
into a problem in convex geometry determined by the local action of H near the fixed points in X. This method of computing global invariants of an action is well-known and heavily used in Geometric Invariant Theory and Symplectic Reduction. However, it is classically only developed for ample line bundles, while we will also need it for semiample ones. This case seems to have received little–if any–interest so far. Consequently, we re-prove the statements we need in detail.
$\kappa (X, -(K_X + D))^{H}\geq 0$
into a problem in convex geometry determined by the local action of H near the fixed points in X. This method of computing global invariants of an action is well-known and heavily used in Geometric Invariant Theory and Symplectic Reduction. However, it is classically only developed for ample line bundles, while we will also need it for semiample ones. This case seems to have received little–if any–interest so far. Consequently, we re-prove the statements we need in detail.
In the log Fano case, the result boils down to a combination of some explicit local computations, some classical results about moment polytopes and a little piece of convex geometry. The semiample case then follows via some perturbation techniques. All of this will be explained in detail in Section 3.
1.2 Conventions
Throughout the paper, we work over the field
![]() $\operatorname {{\mathbb {C}}}$
of complex numbers.
$\operatorname {{\mathbb {C}}}$
of complex numbers.
Since the terminology concerning pairs is slightly ambiguous at times in the literature, let us fix explicitly the notation we will use: For us, a pair
![]() $(X, D)$
consists of a normal variety X and a
$(X, D)$
consists of a normal variety X and a
![]() $\operatorname {{\mathbb {Q}}}$
-Weil divisor
$\operatorname {{\mathbb {Q}}}$
-Weil divisor
![]() $D = \sum a_i D_i$
on X with the property that
$D = \sum a_i D_i$
on X with the property that
![]() $K_X + D$
is
$K_X + D$
is
![]() $\operatorname {{\mathbb {Q}}}$
-Cartier. Here, D may or may not be effective.
$\operatorname {{\mathbb {Q}}}$
-Cartier. Here, D may or may not be effective.
We call
![]() $(X, D)$
log smooth if X is smooth and if D has SNC support. A log smooth pair
$(X, D)$
log smooth if X is smooth and if D has SNC support. A log smooth pair
![]() $(X, D)$
will be called sub-log canonical if
$(X, D)$
will be called sub-log canonical if
![]() $a_i \leq 1$
for all i, and log canonical if additionally D is required to be effective,
$a_i \leq 1$
for all i, and log canonical if additionally D is required to be effective,
![]() $0\leq a_i \leq 1$
. In general, a not necessarily log smooth pair
$0\leq a_i \leq 1$
. In general, a not necessarily log smooth pair
![]() $(X, D)$
is called (sub-)log canonical if for some/any log resolution
$(X, D)$
is called (sub-)log canonical if for some/any log resolution
![]() $f\colon \hat {X} \rightarrow X$
the log smooth pair
$f\colon \hat {X} \rightarrow X$
the log smooth pair
![]() $(\hat {X}, \hat {D})$
is so, where
$(\hat {X}, \hat {D})$
is so, where
![]() $\hat {D}$
is determined by the rules
$\hat {D}$
is determined by the rules
![]() $K_{\hat {X}} + \hat {D} \sim _{\operatorname {{\mathbb {Q}}}} f^*(K_X + D)$
and
$K_{\hat {X}} + \hat {D} \sim _{\operatorname {{\mathbb {Q}}}} f^*(K_X + D)$
and
![]() $f_*\hat {D} = D$
. Similarly, in the definition of a sub-klt pair we do not require D to be effective, while in the definition of a klt pair we do. In other words, our definition of a sub-log canonical pair coincides precisely with the definition of a log canonical pair in [Reference Kollár and Mori18]; similarly for (sub-)klt pairs.
$f_*\hat {D} = D$
. Similarly, in the definition of a sub-klt pair we do not require D to be effective, while in the definition of a klt pair we do. In other words, our definition of a sub-log canonical pair coincides precisely with the definition of a log canonical pair in [Reference Kollár and Mori18]; similarly for (sub-)klt pairs.
2 Reduction of Theorem A to the equivariant non-vanishing
In this section, we reduce the proof of Theorem A to the equivariant non-vanishing problem Theorem C. The main technical tool we will use is the following structure theorem which was recently obtained in [Reference Matsumura and Wang23], building on the previous works [Reference Păun27], [Reference Păun28], [Reference Zhang33], [Reference Lu, Tu, Zhang and Zheng22], [Reference Cao6], [Reference Cao and Höring8], [Reference Cao7], [Reference Cao and Höring9], [Reference Ejiri and Gongyo11], [Reference Campana, Cao and Matsumura5] and [Reference Wang30] among others. We refer to [Reference Debarre10] for the definition of MRC-fibrations (also known as rational quotients).
Theorem 2.1 (Matsumura–Wang [Reference Matsumura and Wang23]).
Let
![]() $(X, \Delta )$
be a projective klt pair with nef anti-log canonical divisor
$(X, \Delta )$
be a projective klt pair with nef anti-log canonical divisor
![]() $-(K_X+\Delta )$
. Then there exists a finite quasi-étale cover
$-(K_X+\Delta )$
. Then there exists a finite quasi-étale cover
![]() $\pi \colon X'\rightarrow X$
such that
$\pi \colon X'\rightarrow X$
such that
![]() $X'$
admis a holomorphic, everywhere defined, MRC-fibration
$X'$
admis a holomorphic, everywhere defined, MRC-fibration
![]() $f\colon X'\rightarrow Y$
. Moreover, the following hold true:
$f\colon X'\rightarrow Y$
. Moreover, the following hold true:
-
(1) Every component of
 $\Delta ' := \pi ^*\Delta $
is dominant over Y, that
$\Delta ' := \pi ^*\Delta $
is dominant over Y, that
 $\Delta '$
is ‘horizontal’.
$\Delta '$
is ‘horizontal’. -
(2) The pair
 $(Y, 0)$
is klt and
$(Y, 0)$
is klt and  .
. -
(3) The general fibre
 $(F, \Delta _F := \Delta '|_F)$
is a (connected) rationally connected klt pair with nef anti-log canonical divisor
$(F, \Delta _F := \Delta '|_F)$
is a (connected) rationally connected klt pair with nef anti-log canonical divisor
 $-(K_F+\Delta _F)$
.
$-(K_F+\Delta _F)$
. -
(4) The morphism f is a locally constant fibration, that is, there exists a group homomorphism
 $\rho \colon \pi _1(Y) \rightarrow \operatorname {\mathrm {Aut}}(F, \Delta _F)$
and an isomorphism over Y where
$\rho \colon \pi _1(Y) \rightarrow \operatorname {\mathrm {Aut}}(F, \Delta _F)$
and an isomorphism over Y where $$ \begin{align*} (X', \Delta') \cong \Big( \widetilde{Y} \times (F, \Delta_F) \Big) / \pi_1(Y), \end{align*} $$
$$ \begin{align*} (X', \Delta') \cong \Big( \widetilde{Y} \times (F, \Delta_F) \Big) / \pi_1(Y), \end{align*} $$
 $\widetilde {Y}$
denotes the universal cover of Y and where
$\widetilde {Y}$
denotes the universal cover of Y and where
 $\pi _1(Y)$
acts diagonally in the natural way on
$\pi _1(Y)$
acts diagonally in the natural way on
 $\widetilde {Y}$
and through
$\widetilde {Y}$
and through
 $\rho $
on
$\rho $
on
 $(F, \Delta _F)$
.
$(F, \Delta _F)$
.
In view of Theorem 2.1 we expect
![]() $-(K_X+\Delta )$
to have sections if and only if
$-(K_X+\Delta )$
to have sections if and only if
![]() $-(K_F+\Delta _F)$
admits sections which are invariant under the action of
$-(K_F+\Delta _F)$
admits sections which are invariant under the action of
![]() $\rho $
. This is made precise below:
$\rho $
. This is made precise below:
Theorem 2.2. Let
![]() $(F, \Delta _F)$
be a rationally connected projective klt pair and assume that the anti-log canonical divisor
$(F, \Delta _F)$
be a rationally connected projective klt pair and assume that the anti-log canonical divisor
![]() $-(K_F + \Delta _F)$
is nef. Then the following assertions are equivalent:
$-(K_F + \Delta _F)$
is nef. Then the following assertions are equivalent:
-
(1) For any projective klt pair
 $(X, \Delta )$
with nef anti-log canonical divisor
$(X, \Delta )$
with nef anti-log canonical divisor
 $-(K_X + \Delta )$
and whose MRC-fibration has
$-(K_X + \Delta )$
and whose MRC-fibration has
 $(F, \Delta _F)$
as its general fibre it holds that
$(F, \Delta _F)$
as its general fibre it holds that  $$ \begin{align*} \kappa\big(X, -(K_X + \Delta)\big)\geq 0. \end{align*} $$
$$ \begin{align*} \kappa\big(X, -(K_X + \Delta)\big)\geq 0. \end{align*} $$
-
(2) There exists a maximal algebraic torus
 $T\subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
such that
$T\subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
such that  $$ \begin{align*} \kappa\Big(F, -\big(K_F + \Delta_F\big)\Big)^T\geq 0. \end{align*} $$
$$ \begin{align*} \kappa\Big(F, -\big(K_F + \Delta_F\big)\Big)^T\geq 0. \end{align*} $$
Recall that an algebraic torus is an algebraic group which is isomorphic to
![]() $(\operatorname {{\mathbb {C}}}^{\times })^r$
for some integer r. In order to prove Theorem 2.2 we need the following elementary result; we include a proof for the sake of completeness:
$(\operatorname {{\mathbb {C}}}^{\times })^r$
for some integer r. In order to prove Theorem 2.2 we need the following elementary result; we include a proof for the sake of completeness:
Lemma 2.3. Let G be a linear algebraic group acting algebraically on a finite dimensional vector space V. Then the following assertions are equivalent:
-
(1) For any commutative, algebraic subgroup
 $H\subseteq G$
it holds that
$H\subseteq G$
it holds that
 $V^H\neq 0$
.
$V^H\neq 0$
. -
(2) For any algebraic torus
 $T\subseteq G$
it holds that
$T\subseteq G$
it holds that
 $V^T\neq 0$
.
$V^T\neq 0$
. -
(3) For some maximal algebraic torus
 $T\subseteq G$
it holds that
$T\subseteq G$
it holds that
 $V^T\neq 0$
.
$V^T\neq 0$
.
Proof. Clearly
![]() $(1)\Rightarrow (2)$
. Regarding the converse, let
$(1)\Rightarrow (2)$
. Regarding the converse, let
![]() $H\subseteq G$
be any commutative, algebraic subgroup. Then H splits as
$H\subseteq G$
be any commutative, algebraic subgroup. Then H splits as
where T is an algebraic torus and U is unipotent, cf. [Reference Milne24, Theorem 16.13]. Consequently,
Here, we used in the last step that the elements of
![]() $U, T$
commute so that the action of U preserves
$U, T$
commute so that the action of U preserves
![]() $V^T$
. Now, by our assumption
$V^T$
. Now, by our assumption
![]() $V^T\neq 0$
. Since (essentially by definition) any algebraic action of a unipotent group on a non-trivial vector space fixes at least one non-trivial vector we conclude that
$V^T\neq 0$
. Since (essentially by definition) any algebraic action of a unipotent group on a non-trivial vector space fixes at least one non-trivial vector we conclude that
![]() $V^H\neq 0$
.
$V^H\neq 0$
.
Finally, the equivalence of
![]() $(2)$
and
$(2)$
and
![]() $(3)$
is clear as any torus
$(3)$
is clear as any torus
![]() $T\subseteq G$
is contained in a maximal one and since any two maximal tori in G are conjugate to each other, see [Reference Milne24, Theorem 17.10].
$T\subseteq G$
is contained in a maximal one and since any two maximal tori in G are conjugate to each other, see [Reference Milne24, Theorem 17.10].
Proof of Theorem 2.2
First, let us prove that
![]() $(2)\Rightarrow (1)$
. Fix
$(2)\Rightarrow (1)$
. Fix
![]() $(X, \Delta )$
a projective klt pair which has
$(X, \Delta )$
a projective klt pair which has
![]() $(F, \Delta _F)$
as general fibre of its MRC-fibration. We want to show that
$(F, \Delta _F)$
as general fibre of its MRC-fibration. We want to show that
![]() $\kappa (X, -(K_X + \Delta ))\geq 0$
. Note that to do so we, may replace
$\kappa (X, -(K_X + \Delta ))\geq 0$
. Note that to do so we, may replace
![]() $(X, \Delta )$
by arbitrary quasi-étale covers, cf. [Reference Ueno29, Theorem 5.13]. In particular, by Theorem 2.1, we may assume that the MRC-fibration
$(X, \Delta )$
by arbitrary quasi-étale covers, cf. [Reference Ueno29, Theorem 5.13]. In particular, by Theorem 2.1, we may assume that the MRC-fibration
![]() $f\colon X \rightarrow Y$
is a locally constant fibration with fibre
$f\colon X \rightarrow Y$
is a locally constant fibration with fibre
![]() $(F, \Delta _F)$
and such that
$(F, \Delta _F)$
and such that
![]() $K_Y = 0$
. Fix a group homomorphism
$K_Y = 0$
. Fix a group homomorphism
![]() $\rho \colon \pi _1(Y)\rightarrow \operatorname {\mathrm {Aut}}(F, \Delta _F)$
such that
$\rho \colon \pi _1(Y)\rightarrow \operatorname {\mathrm {Aut}}(F, \Delta _F)$
such that
Claim. We may assume that the Zariski closure
![]() $H := \overline {\mathrm {Im}\rho } \subseteq \operatorname {\mathrm {Aut}}(F)$
is a connected, commutative, linear algebraic group.
$H := \overline {\mathrm {Im}\rho } \subseteq \operatorname {\mathrm {Aut}}(F)$
is a connected, commutative, linear algebraic group.
Indeed, as X is a projective, the image of
![]() $\pi _1(Y) \overset {\rho }{\rightarrow } \operatorname {\mathrm {Aut}}(F) \rightarrow \operatorname {\mathrm {Aut}}(F)/\operatorname {\mathrm {Aut}}^0(F)$
is finite, see, for example, [Reference Müller25, Lemma 3.4]. Hence, H has only finitely many connected components. Replacing Y by the finite (!) étale cover corresponding to
$\pi _1(Y) \overset {\rho }{\rightarrow } \operatorname {\mathrm {Aut}}(F) \rightarrow \operatorname {\mathrm {Aut}}(F)/\operatorname {\mathrm {Aut}}^0(F)$
is finite, see, for example, [Reference Müller25, Lemma 3.4]. Hence, H has only finitely many connected components. Replacing Y by the finite (!) étale cover corresponding to
and replacing X by
![]() $X':= X\times _Y Y'$
, we may assume that
$X':= X\times _Y Y'$
, we may assume that
![]() $H = H^0$
is connected. Moreover, as F is rationally connected,
$H = H^0$
is connected. Moreover, as F is rationally connected,
![]() $\mathrm {Pic}^0(F) = 0$
and so
$\mathrm {Pic}^0(F) = 0$
and so
![]() $G:= \operatorname {\mathrm {Aut}}^0(F)$
is linear algebraic, see [Reference Brion2, Corollary 2.18]. Thus,
$G:= \operatorname {\mathrm {Aut}}^0(F)$
is linear algebraic, see [Reference Brion2, Corollary 2.18]. Thus,
![]() $H\subseteq G$
is also linear.
$H\subseteq G$
is also linear.
Finally, according to [Reference Greb, Guenancia and Kebekus12, Theorem B], there exists a finite quasi-étale cover
![]() $Y'\rightarrow Y$
such that
$Y'\rightarrow Y$
such that
![]() $Y' = A \times Z$
splits as a product of an abelian variety A and a variety Z with
$Y' = A \times Z$
splits as a product of an abelian variety A and a variety Z with
![]() $\mathcal {O}_Z(K_Z) = \mathcal {O}_Z$
and vanishing augmented irregularity. Since
$\mathcal {O}_Z(K_Z) = \mathcal {O}_Z$
and vanishing augmented irregularity. Since
![]() $G = \operatorname {\mathrm {Aut}}^0(F)$
is linear algebraic, the image of the map
$G = \operatorname {\mathrm {Aut}}^0(F)$
is linear algebraic, the image of the map
![]() $\rho \colon \pi _1(Z) \rightarrow G = \operatorname {\mathrm {Aut}}^0(F)$
is finite by [Reference Greb, Guenancia and Kebekus12, Remark 1.4]. In other words, after another finite étale cover we may assume that X splits as
$\rho \colon \pi _1(Z) \rightarrow G = \operatorname {\mathrm {Aut}}^0(F)$
is finite by [Reference Greb, Guenancia and Kebekus12, Remark 1.4]. In other words, after another finite étale cover we may assume that X splits as
As
![]() $\mathcal {O}_Z(K_Z) = \mathcal {O}_Z$
has sections, it suffices to prove the assertion for
$\mathcal {O}_Z(K_Z) = \mathcal {O}_Z$
has sections, it suffices to prove the assertion for
![]() $(X', \Delta |_{X'})$
and we are thus reduced to the case that
$(X', \Delta |_{X'})$
and we are thus reduced to the case that
![]() $Y = A$
is an abelian variety. In particular, in this case
$Y = A$
is an abelian variety. In particular, in this case
![]() $\pi _1(Y)$
is an abelian group.
$\pi _1(Y)$
is an abelian group.
Let us denote by
![]() $H\subseteq G$
the Zariski-closure of
$H\subseteq G$
the Zariski-closure of
![]() $\mathrm {Im}\rho $
. Then, by continuity,
$\mathrm {Im}\rho $
. Then, by continuity,
and so
![]() $H\subseteq G$
is also commutative. In summary, H is a connected, commutative, linear algebraic group. This concludes the proof of the Claim.
$H\subseteq G$
is also commutative. In summary, H is a connected, commutative, linear algebraic group. This concludes the proof of the Claim.
Let us now continue with the proof of
![]() $(2)\Rightarrow (1)$
. According to Lemma 2.3 and the Claim we may find an integer
$(2)\Rightarrow (1)$
. According to Lemma 2.3 and the Claim we may find an integer
![]() $m\geq 1$
such that
$m\geq 1$
such that
![]() $-m\left (K_F + \Delta _F \right )$
is Cartier and such that
$-m\left (K_F + \Delta _F \right )$
is Cartier and such that
 $$ \begin{align} \bigg( H^0 \Big(F, \mathcal{O}_F \Big( -m \big( K_F + \Delta_F \big) \Big) \Big) \bigg)^H\neq 0. \end{align} $$
$$ \begin{align} \bigg( H^0 \Big(F, \mathcal{O}_F \Big( -m \big( K_F + \Delta_F \big) \Big) \Big) \bigg)^H\neq 0. \end{align} $$
Here, we used that
![]() $G = \operatorname {\mathrm {Aut}}^0(F)$
is linear algebraic. In what follows, we will prove that the elements of the vector space in (2.1) lift to non-zero sections in
$G = \operatorname {\mathrm {Aut}}^0(F)$
is linear algebraic. In what follows, we will prove that the elements of the vector space in (2.1) lift to non-zero sections in
![]() $H^0\left (X, \mathcal {O}_X\left (-m\left (K_X + \Delta \right )\right )\right )$
. Indeed, note that
$H^0\left (X, \mathcal {O}_X\left (-m\left (K_X + \Delta \right )\right )\right )$
. Indeed, note that
Now,
 $$ \begin{align} f_*\mathcal{O}_X\big({-}m(K_{X} + \Delta)\big) & = f_*\mathcal{O}_X\big({-}m(K_{X/Y} + \Delta)\big) \nonumber \\ & = \bigg(\widetilde{Y}\times H^0\Big(F, \mathcal{O}_F\big(-m(K_{F} + \Delta_F)\big)\Big)\bigg)/\pi_1(Y) \end{align} $$
$$ \begin{align} f_*\mathcal{O}_X\big({-}m(K_{X} + \Delta)\big) & = f_*\mathcal{O}_X\big({-}m(K_{X/Y} + \Delta)\big) \nonumber \\ & = \bigg(\widetilde{Y}\times H^0\Big(F, \mathcal{O}_F\big(-m(K_{F} + \Delta_F)\big)\Big)\bigg)/\pi_1(Y) \end{align} $$
is the holomorphically flat vector bundle with fibre ![]() and monodromy representation
and monodromy representation ![]() , c.f. [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21, Proposition 6.3(b)]. In particular,
, c.f. [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21, Proposition 6.3(b)]. In particular,

Here we used in the last line that
![]() $\mathrm {Im}\rho \subseteq H$
and (2.1). Thus,
$\mathrm {Im}\rho \subseteq H$
and (2.1). Thus,
![]() $(2)\Rightarrow (1)$
is settled.
$(2)\Rightarrow (1)$
is settled.
Let us now turn to
![]() $(1)\Rightarrow (2)$
; Given
$(1)\Rightarrow (2)$
; Given
![]() $(F, \Delta _F)$
as in the theorem and
$(F, \Delta _F)$
as in the theorem and
![]() $T\subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
any maximal algebraic torus, our goal is to produce a projective klt pair
$T\subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
any maximal algebraic torus, our goal is to produce a projective klt pair
![]() $(X, \Delta )$
which admits a locally constant fibration
$(X, \Delta )$
which admits a locally constant fibration
![]() $f\colon X \rightarrow Y$
onto a variety Y with
$f\colon X \rightarrow Y$
onto a variety Y with
![]() $K_Y = 0$
and with fibre
$K_Y = 0$
and with fibre
![]() $(F, \Delta _F)$
such that
$(F, \Delta _F)$
such that
To this end, write
![]() $T \cong (\operatorname {{\mathbb {C}}}^\times )^r$
. Fix an abelian variety Y of dimension r and
$T \cong (\operatorname {{\mathbb {C}}}^\times )^r$
. Fix an abelian variety Y of dimension r and ![]() any number of absolute value one which is not a root of unity. Consider the group homomorphism
any number of absolute value one which is not a root of unity. Consider the group homomorphism
![]() $\rho \colon \pi _1(Y)\rightarrow T$
determined by the rule
$\rho \colon \pi _1(Y)\rightarrow T$
determined by the rule
where
![]() $e_1, \ldots e_{2r}$
is some
$e_1, \ldots e_{2r}$
is some ![]() -basis for
-basis for ![]() . Then
. Then
![]() $\mathrm {Im}\rho $
is Euclidean dense in the compact group
$\mathrm {Im}\rho $
is Euclidean dense in the compact group ![]() . In particular,
. In particular,
![]() $\mathrm {Im}\rho $
is Zariski dense in T.
$\mathrm {Im}\rho $
is Zariski dense in T.
Let us consider the complex analytic variety
![]() $X := (\widetilde {Y}\times F)/\pi _1(Y)$
equipped with the
$X := (\widetilde {Y}\times F)/\pi _1(Y)$
equipped with the
![]() $\operatorname {{\mathbb {Q}}}$
-Weil divisor
$\operatorname {{\mathbb {Q}}}$
-Weil divisor
![]() $\Delta := (\widetilde {Y}\times \Delta _F)/\pi _1(Y)$
. Then
$\Delta := (\widetilde {Y}\times \Delta _F)/\pi _1(Y)$
. Then
![]() $(X, \Delta )$
is a projective klt pair with nef anti-log canonical divisor
$(X, \Delta )$
is a projective klt pair with nef anti-log canonical divisor
![]() $-(K_X+\Delta )$
, see [Reference Müller25, Theorem 5.1]. By assumption there exists
$-(K_X+\Delta )$
, see [Reference Müller25, Theorem 5.1]. By assumption there exists
![]() $m\geq 1$
such that
$m\geq 1$
such that
Now, as in (2.3),
 $$ \begin{align*} f_*\mathcal{O}_X(-m(K_{X} + \Delta)) = \bigg(\widetilde{Y}\times H^0\Big(F, \mathcal{O}_F\Big({-}m\big(K_{F} + \Delta_F\big)\Big)\Big)\bigg)/\pi_1(Y) \end{align*} $$
$$ \begin{align*} f_*\mathcal{O}_X(-m(K_{X} + \Delta)) = \bigg(\widetilde{Y}\times H^0\Big(F, \mathcal{O}_F\Big({-}m\big(K_{F} + \Delta_F\big)\Big)\Big)\bigg)/\pi_1(Y) \end{align*} $$
is the holomorphically flat vector bundle with fibre ![]() and monodromy representation
and monodromy representation ![]() . As
. As
![]() $\mathrm {Im}\rho $
is contained in the compact subgroup
$\mathrm {Im}\rho $
is contained in the compact subgroup ![]() , this representation is unitary. It follows that all global sections of
, this representation is unitary. It follows that all global sections of
![]() $f_*\mathcal {O}_X(-m(K_{X/Y} + \Delta ))$
are flat, see, for example, [Reference Wang30, Theorem 2.2(b)]. In other words,
$f_*\mathcal {O}_X(-m(K_{X/Y} + \Delta ))$
are flat, see, for example, [Reference Wang30, Theorem 2.2(b)]. In other words,
Here, in the last step we used that the action of
![]() $\operatorname {\mathrm {Aut}}(F)$
on
$\operatorname {\mathrm {Aut}}(F)$
on ![]() is algebraic and that
is algebraic and that
![]() $\mathrm {Im}\rho \subsetneq T$
is Zariski dense by construction. As we know that
$\mathrm {Im}\rho \subsetneq T$
is Zariski dense by construction. As we know that
![]() $H^0(Y, f_*(-m(K_{X/Y} + \Delta )))\neq 0$
by (2.4) we conclude.
$H^0(Y, f_*(-m(K_{X/Y} + \Delta )))\neq 0$
by (2.4) we conclude.
3 Torus-invariant sections on semiample line bundles
In this section, we want to prove Theorem C under the additional assumption that
![]() $(X, D)$
is log smooth:
$(X, D)$
is log smooth:
Theorem 3.1. Let
![]() $(X, D)$
be a projective, log smooth, sub-log canonical pair such that
$(X, D)$
be a projective, log smooth, sub-log canonical pair such that
![]() $-(K_X+D)$
is semiample. Then for any algebraic torus
$-(K_X+D)$
is semiample. Then for any algebraic torus
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X, D)$
it holds that
$T\subseteq \operatorname {\mathrm {Aut}}(X, D)$
it holds that
To prove Theorem 3.1, we will employ some discrete methods from toric geometry. Let us start by introducing the following concept:
Definition 3.2. Let X be a normal variety and let
![]() $G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup. A coherent sheaf
$G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup. A coherent sheaf
![]() $\mathscr {L}$
on X is said to be G-invariant if
$\mathscr {L}$
on X is said to be G-invariant if
![]() $g^*\mathscr {L}\cong \mathscr {L}$
for all
$g^*\mathscr {L}\cong \mathscr {L}$
for all
![]() $g\in G$
. In this case, we say that
$g\in G$
. In this case, we say that
![]() $\mathscr {L}$
is G-linearizable if the action of G on X may be lifted to an action of G on the total space of
$\mathscr {L}$
is G-linearizable if the action of G on X may be lifted to an action of G on the total space of
![]() $\mathscr {L}$
via sheaf automorphisms. A G-linearization of
$\mathscr {L}$
via sheaf automorphisms. A G-linearization of
![]() $\mathscr {L}$
is a choice of such a lift. See [Reference Mumford, Fogarty and Kirwan26, Definition 1.6] for a more formal definition of linearizations.
$\mathscr {L}$
is a choice of such a lift. See [Reference Mumford, Fogarty and Kirwan26, Definition 1.6] for a more formal definition of linearizations.
Example 3.3. Let X be a normal variety, let
![]() $G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup and let
$G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup and let
![]() $\mathscr {L}, \mathscr {L}_1, \mathscr {L}_2$
be G-linearized coherent sheaves on X. Then also
$\mathscr {L}, \mathscr {L}_1, \mathscr {L}_2$
be G-linearized coherent sheaves on X. Then also
![]() $\mathscr {L}^{*}$
and
$\mathscr {L}^{*}$
and
![]() $\mathscr {L}_1\otimes \mathscr {L}_2$
inherit natural G-linearizations.
$\mathscr {L}_1\otimes \mathscr {L}_2$
inherit natural G-linearizations.
Definition 3.4. Let X be a normal variety, let
![]() $G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup and let
$G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup and let
![]() $\mathscr {L}$
be a G-linearized, coherent, reflexive
$\mathscr {L}$
be a G-linearized, coherent, reflexive
![]() $\mathcal {O}_X$
-module of rank one. Then G acts on
$\mathcal {O}_X$
-module of rank one. Then G acts on
![]() $H^0(X, (\mathscr {L}^{\otimes m})^{**})$
for any integer m and we will say that that
$H^0(X, (\mathscr {L}^{\otimes m})^{**})$
for any integer m and we will say that that
![]() $\kappa (X, \mathscr {L})^G \geq 0$
if and only if
$\kappa (X, \mathscr {L})^G \geq 0$
if and only if
 $$ \begin{align*} \bigoplus_{m=1}^\infty H^0\Big(X, \left(\mathscr{L}^{\otimes m}\right)^{**}\Big)^G \neq 0. \end{align*} $$
$$ \begin{align*} \bigoplus_{m=1}^\infty H^0\Big(X, \left(\mathscr{L}^{\otimes m}\right)^{**}\Big)^G \neq 0. \end{align*} $$
Example 3.5. Consider
![]() $X= \operatorname {{\mathbb {P}}}^1$
equipped with the line bundle
$X= \operatorname {{\mathbb {P}}}^1$
equipped with the line bundle
![]() $\mathscr {L} = \mathcal {O}_{\operatorname {{\mathbb {P}}}^1}(-1)$
.
$\mathscr {L} = \mathcal {O}_{\operatorname {{\mathbb {P}}}^1}(-1)$
.
-
(1) Let
 . Then
. Then
 $\mathscr {L}$
is clearly G-invariant. However, this action is (rather famously) not linearizable, see, for example, [Reference Brion3, Example 4.2.4].
$\mathscr {L}$
is clearly G-invariant. However, this action is (rather famously) not linearizable, see, for example, [Reference Brion3, Example 4.2.4]. -
(2) Let
 $G = T \subsetneq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
be the subgroup of (equivalence classes of) diagonal matrices. Then
$G = T \subsetneq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
be the subgroup of (equivalence classes of) diagonal matrices. Then
 $ \operatorname {{\mathbb {C}}}^\times \cong T \subsetneq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
is a maximal torus acting via
$ \operatorname {{\mathbb {C}}}^\times \cong T \subsetneq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
is a maximal torus acting via  and this action is linearizable. In fact, for any
and this action is linearizable. In fact, for any  an explicit choice of lifting is provided by
an explicit choice of lifting is provided by  . Here we identify, as per usual,
. Here we identify, as per usual,  .
.
Example 3.6. Let X be a normal variety and let
![]() $G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup. Then the anti-canonical bundle
$G\subseteq \operatorname {\mathrm {Aut}}(X)$
be a subgroup. Then the anti-canonical bundle
![]() $\mathcal {O}_X(-K_X)$
admits a natural linearization given by push-forward of forms:
$\mathcal {O}_X(-K_X)$
admits a natural linearization given by push-forward of forms: ![]() . Recall that in local coordinates
. Recall that in local coordinates
![]() $\varphi _*$
is simply defined by the formula
$\varphi _*$
is simply defined by the formula
 $$ \begin{align*} \left(\varphi_*\left(f \frac{\partial}{\partial z_1}\wedge\ldots\wedge\frac{\partial}{\partial z_n}\right)\right)(\varphi(x)) = f(x) \cdot d\varphi\left(\frac{\partial}{\partial z_1}\right)\wedge\ldots\wedge d\varphi \left(\frac{\partial}{\partial z_n}\right), \end{align*} $$
$$ \begin{align*} \left(\varphi_*\left(f \frac{\partial}{\partial z_1}\wedge\ldots\wedge\frac{\partial}{\partial z_n}\right)\right)(\varphi(x)) = f(x) \cdot d\varphi\left(\frac{\partial}{\partial z_1}\right)\wedge\ldots\wedge d\varphi \left(\frac{\partial}{\partial z_n}\right), \end{align*} $$
where
![]() $\varphi \colon X\rightarrow X$
is any automorphism.
$\varphi \colon X\rightarrow X$
is any automorphism.
Example 3.7. Let D be a Cartier divisor on X and assume that it is invariant (as a subset of X) under the action of G. Then also
![]() $\mathcal {O}_X(D)$
carries a natural G-linearization as a subsheaf of
$\mathcal {O}_X(D)$
carries a natural G-linearization as a subsheaf of
![]() $\operatorname {{\mathbb {C}}}(X)$
, which is induced by the pull-back of functions:
$\operatorname {{\mathbb {C}}}(X)$
, which is induced by the pull-back of functions: ![]() . Note that we take the inverse in order to obtain a left-action.
. Note that we take the inverse in order to obtain a left-action.
Similarly,
![]() $\Omega ^1_X$
admits a natural linearization given by
$\Omega ^1_X$
admits a natural linearization given by ![]() .
.
In conclusion, whenever
![]() $(X, D)$
is a pair, then the line bundle
$(X, D)$
is a pair, then the line bundle
![]() $\mathcal {O}_X(-m(K_X + D))$
carries a natural
$\mathcal {O}_X(-m(K_X + D))$
carries a natural
![]() $\operatorname {\mathrm {Aut}}(X, D)$
-linearization for all
$\operatorname {\mathrm {Aut}}(X, D)$
-linearization for all
![]() $m\in \operatorname {{\mathbb {Z}}}$
such that
$m\in \operatorname {{\mathbb {Z}}}$
such that
![]() $m(K_X+D)$
is Cartier.
$m(K_X+D)$
is Cartier.
In the following, we will require some standard facts about algebraic tori and their representations which we recall below: Let
![]() $T \cong (\operatorname {{\mathbb {C}}}^\times )^r$
be an algebraic torus. Then its character lattice
$T \cong (\operatorname {{\mathbb {C}}}^\times )^r$
be an algebraic torus. Then its character lattice
![]() $M := \operatorname {\mathrm {Hom}}(T, \operatorname {{\mathbb {C}}}^\times )$
is a finitely generated free abelian group of rank
$M := \operatorname {\mathrm {Hom}}(T, \operatorname {{\mathbb {C}}}^\times )$
is a finitely generated free abelian group of rank ![]() . Explicitly, if
. Explicitly, if
![]() $T = (\operatorname {{\mathbb {C}}}^\times )^r$
then
$T = (\operatorname {{\mathbb {C}}}^\times )^r$
then
In the sequel, following standard practice, we will consider M as an additive group
![]() $(M, +)$
. In particular, the neutral element
$(M, +)$
. In particular, the neutral element
![]() $0\in M$
corresponds to the trivial homomorphism
$0\in M$
corresponds to the trivial homomorphism
![]() $t\mapsto 1$
. We will also consider the real vector space
$t\mapsto 1$
. We will also consider the real vector space
![]() $M_{\operatorname {{\mathbb {R}}}} := M \otimes _{\operatorname {{\mathbb {Z}}}} \operatorname {{\mathbb {R}}}$
.
$M_{\operatorname {{\mathbb {R}}}} := M \otimes _{\operatorname {{\mathbb {Z}}}} \operatorname {{\mathbb {R}}}$
.
Now, let
![]() $\rho \colon T\rightarrow \operatorname {\mathrm {GL}}(V)$
be an algebraic representation of T on a finite-dimensional complex vector space V (we also say that V is a T-module). Then the action of T can be diagonalised, there exists a
$\rho \colon T\rightarrow \operatorname {\mathrm {GL}}(V)$
be an algebraic representation of T on a finite-dimensional complex vector space V (we also say that V is a T-module). Then the action of T can be diagonalised, there exists a
![]() $\operatorname {{\mathbb {C}}}$
-basis
$\operatorname {{\mathbb {C}}}$
-basis
![]() $e_1, \ldots , e_m$
, called a basis of eigenvectors, for V such that
$e_1, \ldots , e_m$
, called a basis of eigenvectors, for V such that
for some
![]() $w_1, \ldots , w_m \in M= \operatorname {\mathrm {Hom}}(T, \operatorname {{\mathbb {C}}}^\times )$
called the weights of the representation
$w_1, \ldots , w_m \in M= \operatorname {\mathrm {Hom}}(T, \operatorname {{\mathbb {C}}}^\times )$
called the weights of the representation
![]() $\rho $
. A representation of T is determined up to isomorphism by its weights.
$\rho $
. A representation of T is determined up to isomorphism by its weights.
Definition 3.8. Let X be a normal projective variety, let
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus and let
$T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus and let
![]() $\mathscr {L}$
be a coherent sheaf on X, linearized for the action of T. Then T acts naturally on the space
$\mathscr {L}$
be a coherent sheaf on X, linearized for the action of T. Then T acts naturally on the space
![]() $H^0(X, \mathscr {L})$
. We let
$H^0(X, \mathscr {L})$
. We let
![]() $W_{\Gamma }(X, \mathscr {L}) \subseteq M$
denote the set of weights of this action. Moreover, we denote the convex hull of
$W_{\Gamma }(X, \mathscr {L}) \subseteq M$
denote the set of weights of this action. Moreover, we denote the convex hull of
![]() $W_{\Gamma }(X, \mathscr {L})$
in
$W_{\Gamma }(X, \mathscr {L})$
in
![]() $M_{\operatorname {{\mathbb {R}}}}$
by
$M_{\operatorname {{\mathbb {R}}}}$
by
![]() $P_{\Gamma }(X, \mathscr {L})$
and call this the section polytope of
$P_{\Gamma }(X, \mathscr {L})$
and call this the section polytope of
![]() $\mathscr {L}$
.
$\mathscr {L}$
.
Notation 3.9. From now on and for the rest of this section, we let X denote a smooth projective variety and we fix an algebraic torus
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X)$
. Then the set of fixed points
$T\subseteq \operatorname {\mathrm {Aut}}(X)$
. Then the set of fixed points ![]() is a non-empty, closed, smooth subvariety of X, see [Reference Milne24, Theorem 13.1, Proposition 13.20]. We let
is a non-empty, closed, smooth subvariety of X, see [Reference Milne24, Theorem 13.1, Proposition 13.20]. We let
![]() $X^T = Y_1 \sqcup \ldots \sqcup Y_c$
denote the decomposition of
$X^T = Y_1 \sqcup \ldots \sqcup Y_c$
denote the decomposition of
![]() $X^T$
into its connected components. Moreover, for any
$X^T$
into its connected components. Moreover, for any
![]() $i = 1,\ldots , c$
let us fix a point
$i = 1,\ldots , c$
let us fix a point
![]() $y_i \in Y_i$
.
$y_i \in Y_i$
.
Definition 3.10. Let
![]() $\mathscr {L}$
be a line bundle on X, linearized for the action of T. Then T acts on the one-dimensional
$\mathscr {L}$
be a line bundle on X, linearized for the action of T. Then T acts on the one-dimensional
![]() $\operatorname {{\mathbb {C}}}$
-vector space
$\operatorname {{\mathbb {C}}}$
-vector space
![]() $\mathscr {L}|_{y_i}$
for any
$\mathscr {L}|_{y_i}$
for any
![]() $i = 1,\ldots , c$
, with weight
$i = 1,\ldots , c$
, with weight
![]() $\mu _i$
say. Let us set
$\mu _i$
say. Let us set
![]() $W_{\mu }(X, \mathscr {L}) := \{ \mu _1, \ldots , \mu _c \} \subseteq M$
. The convex hull
$W_{\mu }(X, \mathscr {L}) := \{ \mu _1, \ldots , \mu _c \} \subseteq M$
. The convex hull
![]() $P_{\mu }(X, \mathscr {L})$
of
$P_{\mu }(X, \mathscr {L})$
of
![]() $W_{\mu }(X, \mathscr {L})$
in
$W_{\mu }(X, \mathscr {L})$
in ![]() is called the moment polytope.
is called the moment polytope.
Remark 3.11. Note that
![]() $\mu _i$
does not depend on the choice of
$\mu _i$
does not depend on the choice of
![]() $y_i \in Y_i$
. Indeed, let
$y_i \in Y_i$
. Indeed, let
![]() $y_i\in U \subseteq X$
be a T-invariant affine open neighbourhood which exists by [Reference Brion3, Corollary 5.3.6]. Pick a section
$y_i\in U \subseteq X$
be a T-invariant affine open neighbourhood which exists by [Reference Brion3, Corollary 5.3.6]. Pick a section
![]() $\sigma \in \mathscr {L}(U)$
which does not vanish at
$\sigma \in \mathscr {L}(U)$
which does not vanish at
![]() $y_i$
. Then the weight
$y_i$
. Then the weight
![]() $\mu _y$
of the action of T on
$\mu _y$
of the action of T on
![]() $\mathscr {L}|_{y}$
is given by
$\mathscr {L}|_{y}$
is given by ![]() for all
for all
![]() $y\in Y_i\cap U$
such that
$y\in Y_i\cap U$
such that
![]() $\sigma (y)\neq 0$
. This shows that the map
$\sigma (y)\neq 0$
. This shows that the map
![]() $Y_i \rightarrow M$
,
$Y_i \rightarrow M$
,
![]() $y\mapsto \mu _y$
is continuous, hence constant.
$y\mapsto \mu _y$
is continuous, hence constant.
Example 3.12. Continuing Example 3.5, let
![]() $\operatorname {{\mathbb {C}}}^{\times }\subseteq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
act on
$\operatorname {{\mathbb {C}}}^{\times }\subseteq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
act on ![]() via the rule
via the rule ![]() . Then
. Then
![]() $W_{\mu }(\operatorname {{\mathbb {P}}}^1, \mathcal {O}(-1)) = \{ w, w+1\} \subseteq M = \operatorname {{\mathbb {Z}}}$
and, consequently,
$W_{\mu }(\operatorname {{\mathbb {P}}}^1, \mathcal {O}(-1)) = \{ w, w+1\} \subseteq M = \operatorname {{\mathbb {Z}}}$
and, consequently, ![]() .
.
The following result is essentially taken from [Reference Buczyński and Wiśniewski4, Lemma 2.4] where it is stated only for ample bundles. The proof generalises to the semiample setting without difficulties.
Proposition 3.13. Let X be a smooth projective variety, let
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus and let
$T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus and let
![]() $\mathscr {L}$
be a semiample line bundle on X, linearized for the action of T.
$\mathscr {L}$
be a semiample line bundle on X, linearized for the action of T.
Then for any integer
![]() $m\geq 1$
the following hold true:
$m\geq 1$
the following hold true:
-
(1)
 $mP_{\Gamma }(X, \mathscr {L}) \subseteq P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
and
$mP_{\Gamma }(X, \mathscr {L}) \subseteq P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
and
 $mP_{\mu }(X, \mathscr {L}) = P_{\mu }(X, \mathscr {L}^{\otimes m})$
as subsets of
$mP_{\mu }(X, \mathscr {L}) = P_{\mu }(X, \mathscr {L}^{\otimes m})$
as subsets of  ,
, -
(2)
 $P_{\Gamma }(X, \mathscr {L}) \subseteq P_{\mu }(X, \mathscr {L}),$
and
$P_{\Gamma }(X, \mathscr {L}) \subseteq P_{\mu }(X, \mathscr {L}),$
and -
(3) if
 $\mathscr {L}$
is basepoint free then
$\mathscr {L}$
is basepoint free then
 $P_{\Gamma }(X, \mathscr {L}) = P_{\mu }(X, \mathscr {L})$
.
$P_{\Gamma }(X, \mathscr {L}) = P_{\mu }(X, \mathscr {L})$
.
Proof.
![]() $(1)$
: Clearly
$(1)$
: Clearly
![]() $mW_{\Gamma }(X, \mathscr {L}) \subseteq W_{\Gamma }(X, \mathscr {L}^{\otimes m})$
for if
$mW_{\Gamma }(X, \mathscr {L}) \subseteq W_{\Gamma }(X, \mathscr {L}^{\otimes m})$
for if
![]() $w_1, \ldots , w_m \in W_{\Gamma }(X, \mathscr {L})$
are weights for the action of T on
$w_1, \ldots , w_m \in W_{\Gamma }(X, \mathscr {L})$
are weights for the action of T on
![]() $H^0(X, \mathscr {L})$
with corresponding eigenvectors
$H^0(X, \mathscr {L})$
with corresponding eigenvectors
![]() $\sigma _1, \ldots , \sigma _m$
then
$\sigma _1, \ldots , \sigma _m$
then
is an eigenvector for the action of T of weight
![]() $w_1 + \ldots + w_m \in mW_{\Gamma }(X, \mathscr {L})$
. We deduce that
$w_1 + \ldots + w_m \in mW_{\Gamma }(X, \mathscr {L})$
. We deduce that
![]() $mP_{\Gamma }(X, \mathscr {L}) \subseteq P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
.
$mP_{\Gamma }(X, \mathscr {L}) \subseteq P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
.
That
![]() $mP_{\mu }(X, \mathscr {L}) = P_{\mu }(X, \mathscr {L}^{\otimes m})$
is obvious for if
$mP_{\mu }(X, \mathscr {L}) = P_{\mu }(X, \mathscr {L}^{\otimes m})$
is obvious for if
![]() $y\in X^T$
and if
$y\in X^T$
and if
![]() $\mu $
is the weight for the action of T on
$\mu $
is the weight for the action of T on
![]() $\mathscr {L}|_y$
then the weight of the action on
$\mathscr {L}|_y$
then the weight of the action on
![]() $\mathscr {L}^{\otimes m}|_y$
is just
$\mathscr {L}^{\otimes m}|_y$
is just
![]() $m\mu $
.
$m\mu $
.
To prove
![]() $(2)$
, the argument in [Reference Buczyński and Wiśniewski4, Lemma 2.4(2)] applies ad verbatim. Note that to prove Theorem 3.1 we will not make use of this inclusion.
$(2)$
, the argument in [Reference Buczyński and Wiśniewski4, Lemma 2.4(2)] applies ad verbatim. Note that to prove Theorem 3.1 we will not make use of this inclusion.
Regarding
![]() $(3)$
, the proof of [Reference Buczyński and Wiśniewski4, Lemma 2.4(3)] again goes through without changes. However, as the argument is so elementary we want to quickly repeat it here: Fix
$(3)$
, the proof of [Reference Buczyński and Wiśniewski4, Lemma 2.4(3)] again goes through without changes. However, as the argument is so elementary we want to quickly repeat it here: Fix
![]() $y\in X^T$
and let us denote by
$y\in X^T$
and let us denote by
![]() $\mu $
the weight of the action of T on
$\mu $
the weight of the action of T on
![]() $\mathscr {L}|_y$
. As
$\mathscr {L}|_y$
. As
![]() $\mathscr {L}$
is generated by global sections we have the short exact sequence of T-modules
$\mathscr {L}$
is generated by global sections we have the short exact sequence of T-modules
As it is well-known that any short exact sequence of T-modules splits, we find an eigenvector
![]() $\sigma \in \mathrm {H}^0(X, \mathscr {L})$
for the action of T of weight
$\sigma \in \mathrm {H}^0(X, \mathscr {L})$
for the action of T of weight
![]() $\mu $
. This proves that
$\mu $
. This proves that
![]() $W_{\mu }(X, \mathscr {L}) \subseteq W_{\Gamma }(X, \mathscr {L})$
. We infer that
$W_{\mu }(X, \mathscr {L}) \subseteq W_{\Gamma }(X, \mathscr {L})$
. We infer that
![]() $P_{\mu }(X, \mathscr {L}) \subseteq P_{\Gamma }(X, \mathscr {L})$
and so the result follows from
$P_{\mu }(X, \mathscr {L}) \subseteq P_{\Gamma }(X, \mathscr {L})$
and so the result follows from
![]() $(2)$
.
$(2)$
.
Corollary 3.14. Let X be a smooth projective variety, let
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus and let
$T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus and let
![]() $\mathscr {L}$
be a semiample line bundle on X, linearized for the action of T.
$\mathscr {L}$
be a semiample line bundle on X, linearized for the action of T.
Then
![]() $\kappa (X, \mathscr {L})^T \geq 0$
if and only if the origin
$\kappa (X, \mathscr {L})^T \geq 0$
if and only if the origin
![]() $0\in M$
is contained in
$0\in M$
is contained in
![]() $P_{\mu }(X, \mathscr {L})$
.
$P_{\mu }(X, \mathscr {L})$
.
Proof. Let us start by proving that
Indeed, the first equivalence holds true by the very definition of
![]() $W_{\Gamma }$
and also the second ‘
$W_{\Gamma }$
and also the second ‘
![]() $\Rightarrow $
’-implication is obvious. Regrading the converse, assume that
$\Rightarrow $
’-implication is obvious. Regrading the converse, assume that
![]() $0\in P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
. Let us denote the weights of the action of T on
$0\in P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
. Let us denote the weights of the action of T on
![]() $\mathrm {H}^0(X, \mathscr {L}^{\otimes m})$
by
$\mathrm {H}^0(X, \mathscr {L}^{\otimes m})$
by
![]() $w_1, \ldots , w_\ell $
and let
$w_1, \ldots , w_\ell $
and let
![]() $\sigma _1, \ldots , \sigma _\ell $
be a corresponding basis of eigenvectors. Now
$\sigma _1, \ldots , \sigma _\ell $
be a corresponding basis of eigenvectors. Now
![]() $0\in P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
simply means that there exist real numbers
$0\in P_{\Gamma }(X, \mathscr {L}^{\otimes m})$
simply means that there exist real numbers
![]() $0\leq \lambda _i \leq 1$
such that
$0\leq \lambda _i \leq 1$
such that
![]() $\sum \lambda _i = 1$
and
$\sum \lambda _i = 1$
and
 $$ \begin{align*} \sum_{i=1}^\ell \lambda_i w_i = 0. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^\ell \lambda_i w_i = 0. \end{align*} $$
In fact, by Proposition 3.15 below one can assume the
![]() $\lambda _i$
’s to be rational numbers, say
$\lambda _i$
’s to be rational numbers, say
![]() $\lambda _i = \frac {p_i}{q_i}$
. Set
$\lambda _i = \frac {p_i}{q_i}$
. Set
![]() $k_i := q_1 \cdot \ldots \cdot q_{i-1} \cdot p_i \cdot q_{i+1} \cdot \ldots \cdot q_\ell \in \operatorname {{\mathbb {Z}}}$
. Then
$k_i := q_1 \cdot \ldots \cdot q_{i-1} \cdot p_i \cdot q_{i+1} \cdot \ldots \cdot q_\ell \in \operatorname {{\mathbb {Z}}}$
. Then
 $$ \begin{align*} \sum_{i=1}^\ell k_i w_i = 0. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^\ell k_i w_i = 0. \end{align*} $$
But this in turn just means that
is an eigenvector for the action of T of weight
![]() $\sum k_iw_i = 0$
. In other words, denoting
$\sum k_iw_i = 0$
. In other words, denoting
![]() $k = k_1 +\ldots + k_\ell $
we deduce that
$k = k_1 +\ldots + k_\ell $
we deduce that
where we applied Proposition 3.13. This concludes the proof of (3.1).
But now, a further application of Proposition 3.13 yields
for sufficiently large
![]() $m\geq 1$
. In view of (3.1), we deduce that
$m\geq 1$
. In view of (3.1), we deduce that
![]() $\kappa (X, \mathscr {L})^T \geq 0$
if and only if
$\kappa (X, \mathscr {L})^T \geq 0$
if and only if
![]() $0 \in P_{\mu }(X, \mathscr {L})$
as proclaimed.
$0 \in P_{\mu }(X, \mathscr {L})$
as proclaimed.
The following result is just basic linear algebra. Due to the inability of the author to locate a reference in the literature we include a proof anyway.
Proposition 3.15. Let M be a finitely generated free abelian group, let
![]() $w_1, \ldots , w_m\in M_{\operatorname {{\mathbb {Q}}}} := M\otimes \operatorname {{\mathbb {Q}}}$
be a finite subset and let
$w_1, \ldots , w_m\in M_{\operatorname {{\mathbb {Q}}}} := M\otimes \operatorname {{\mathbb {Q}}}$
be a finite subset and let
![]() $P\subseteq M_{\operatorname {{\mathbb {R}}}}$
be its convex hull. Then
$P\subseteq M_{\operatorname {{\mathbb {R}}}}$
be its convex hull. Then
 $$ \begin{align*} P \cap M_{\operatorname{{\mathbb{Q}}}} = P_{\operatorname{{\mathbb{Q}}}} := \left\{ \sum_{i=1}^m \lambda_i w_i \hspace{0.1cm} \Big| \hspace{0.1cm} 0\leq \lambda_i, \hspace{0.1cm} \lambda_i \in \operatorname{{\mathbb{Q}}}, \hspace{0.1cm} \sum_{i=1}^m \lambda_i = 1 \right\}. \end{align*} $$
$$ \begin{align*} P \cap M_{\operatorname{{\mathbb{Q}}}} = P_{\operatorname{{\mathbb{Q}}}} := \left\{ \sum_{i=1}^m \lambda_i w_i \hspace{0.1cm} \Big| \hspace{0.1cm} 0\leq \lambda_i, \hspace{0.1cm} \lambda_i \in \operatorname{{\mathbb{Q}}}, \hspace{0.1cm} \sum_{i=1}^m \lambda_i = 1 \right\}. \end{align*} $$
Proof. Clearly ![]() . Regarding the converse, fix
. Regarding the converse, fix
![]() $w\in P \cap M_{\operatorname {{\mathbb {Q}}}}$
. After replacing
$w\in P \cap M_{\operatorname {{\mathbb {Q}}}}$
. After replacing
![]() $w_i$
by
$w_i$
by
![]() $w_i - w$
we may assume that
$w_i - w$
we may assume that
![]() $w= 0$
. Write
$w= 0$
. Write
 $$ \begin{align*} w = \sum_{i=1}^m \lambda^*_i w_i \end{align*} $$
$$ \begin{align*} w = \sum_{i=1}^m \lambda^*_i w_i \end{align*} $$
for some real numbers
![]() $0\leq \lambda ^*_i$
such that
$0\leq \lambda ^*_i$
such that
![]() $ \sum _{i=1}^m \lambda ^*_i = 1$
. Forgetting some of the
$ \sum _{i=1}^m \lambda ^*_i = 1$
. Forgetting some of the
![]() $w_i$
if necessary, we may assume that
$w_i$
if necessary, we may assume that
![]() $\lambda ^*_i>0$
for all
$\lambda ^*_i>0$
for all
![]() $i=1,\ldots , m$
.
$i=1,\ldots , m$
.
Now, consider the rational system of linear equations
 $$ \begin{align*}\left\{ \left. \left(\begin{matrix} \lambda_1 \\ \vdots \\ \lambda_m \end{matrix} \right) \hspace{0.1cm} \right| \hspace{0.1cm} \sum_{i=1}^m \lambda_i w_i = 0, \hspace{0.1cm} \sum_{i=1}^m \lambda_i = 1 \right\}. \end{align*} $$
$$ \begin{align*}\left\{ \left. \left(\begin{matrix} \lambda_1 \\ \vdots \\ \lambda_m \end{matrix} \right) \hspace{0.1cm} \right| \hspace{0.1cm} \sum_{i=1}^m \lambda_i w_i = 0, \hspace{0.1cm} \sum_{i=1}^m \lambda_i = 1 \right\}. \end{align*} $$
By assumption it admits the real solution
![]() $\lambda ^* := (\lambda _1^*, \ldots , \lambda _m^*)$
such that
$\lambda ^* := (\lambda _1^*, \ldots , \lambda _m^*)$
such that
![]() $\lambda _i^*> 0$
. Let
$\lambda _i^*> 0$
. Let
![]() $(\lambda _1, \ldots , \lambda _m)$
be any rational solution which is sufficiently close to
$(\lambda _1, \ldots , \lambda _m)$
be any rational solution which is sufficiently close to
![]() $\lambda ^*$
. Then also
$\lambda ^*$
. Then also
![]() $\lambda _i>0$
and so
$\lambda _i>0$
and so
![]() $w = \sum _{i=1}^m \lambda _i w_i$
with rational
$w = \sum _{i=1}^m \lambda _i w_i$
with rational
![]() $\lambda _i$
as required.
$\lambda _i$
as required.
Example 3.16. Continuing Example 3.5, let
![]() $\operatorname {{\mathbb {C}}}^{\times }\subseteq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
act on
$\operatorname {{\mathbb {C}}}^{\times }\subseteq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
act on
![]() $\mathcal {O}(-1)$
via the rule
$\mathcal {O}(-1)$
via the rule ![]() . By Example 3.12 the moment polytope for the induced action of T on
. By Example 3.12 the moment polytope for the induced action of T on
![]() $\mathcal {O}(m)$
is given by
$\mathcal {O}(m)$
is given by
We deduce that
![]() $\kappa (\operatorname {{\mathbb {P}}}^1, \mathcal {O}(1))^T \geq 0$
if and only if
$\kappa (\operatorname {{\mathbb {P}}}^1, \mathcal {O}(1))^T \geq 0$
if and only if
![]() $w=0$
or
$w=0$
or
![]() $w=-1$
.
$w=-1$
.
Proposition 3.17. Let X be a smooth projective variety and let
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus. Choose a fixed point
$T\subseteq \operatorname {\mathrm {Aut}}(X)$
be an algebraic torus. Choose a fixed point
![]() $y\in X^T$
and denote by
$y\in X^T$
and denote by
![]() $\nu _1, \ldots , \nu _n$
the weights of the natural isotropy action of T on the cotangent space
$\nu _1, \ldots , \nu _n$
the weights of the natural isotropy action of T on the cotangent space
![]() $\Omega _X^1|_{y}$
.
$\Omega _X^1|_{y}$
.
-
(1) The weight
 $\mu $
of the action of T on
$\mu $
of the action of T on
 $\mathcal {O}_X(-K_X)|_y$
satisfies the equation
$\mathcal {O}_X(-K_X)|_y$
satisfies the equation  $$ \begin{align*} \mu = -(\nu_1 + \ldots + \nu_n). \end{align*} $$
$$ \begin{align*} \mu = -(\nu_1 + \ldots + \nu_n). \end{align*} $$
-
(2) Let D be a T-invariant prime divisor on X and let us denote by
 $\mu $
the weight of the action of T on
$\mu $
the weight of the action of T on
 $\mathcal {O}_X(-D)|_y$
. Then
$\mathcal {O}_X(-D)|_y$
. Then
 $\mu = \sum _i m_i \cdot \nu _i$
for some non-negative integers
$\mu = \sum _i m_i \cdot \nu _i$
for some non-negative integers
 $m_i \geq 0$
. Moreover:
$m_i \geq 0$
. Moreover:-
(a) If
 $y\notin D$
then
$y\notin D$
then
 $\mu = 0$
.
$\mu = 0$
. -
(b) If
 $y\in D$
is a smooth point of D then the natural isomorphism is compatible with the action of T. In particular,
$y\in D$
is a smooth point of D then the natural isomorphism is compatible with the action of T. In particular, $$ \begin{align*}\mathcal{O}_X(-D)|_y\cong \mathcal{N}^*_{D/X}|_{y} \subseteq \Omega_X^1|_{y}\end{align*} $$
$$ \begin{align*}\mathcal{O}_X(-D)|_y\cong \mathcal{N}^*_{D/X}|_{y} \subseteq \Omega_X^1|_{y}\end{align*} $$
 $\mu = \nu _i$
for some i.
$\mu = \nu _i$
for some i.
-
Proof. The first statement is clear as
![]() $\mathcal {O}_X(-K_X)|_y = \det (\mathrm {T}X|_{y})$
as T-modules.
$\mathcal {O}_X(-K_X)|_y = \det (\mathrm {T}X|_{y})$
as T-modules.
Regarding item
![]() $(2)$
, we claim that there exists a local defining equation
$(2)$
, we claim that there exists a local defining equation
![]() $f \in \mathcal {O}_{X, y}$
of D such that
$f \in \mathcal {O}_{X, y}$
of D such that
Indeed, let
![]() $f' \in \mathcal {O}_{X, y}$
be any local defining equation. Since the action of T on
$f' \in \mathcal {O}_{X, y}$
be any local defining equation. Since the action of T on
![]() $\mathcal {O}_{X, y}$
is algebraic, the
$\mathcal {O}_{X, y}$
is algebraic, the
![]() $\operatorname {{\mathbb {C}}}$
-vector space spanned by
$\operatorname {{\mathbb {C}}}$
-vector space spanned by ![]() is finite-dimensional, see [Reference Milne24, Corollary 4.8]. Let
is finite-dimensional, see [Reference Milne24, Corollary 4.8]. Let
![]() $f_1, \ldots , f_r$
be a basis of T-eigenvectors, of weights
$f_1, \ldots , f_r$
be a basis of T-eigenvectors, of weights
![]() $\mu _i$
say. Since
$\mu _i$
say. Since ![]() is a local defining equation of D for any
is a local defining equation of D for any
![]() $t\in T$
by Example 3.7, it follows that
$t\in T$
by Example 3.7, it follows that
![]() $f_i$
vanishes along D for any i. On the other hand, since
$f_i$
vanishes along D for any i. On the other hand, since
![]() $f'$
is a
$f'$
is a
![]() $\operatorname {{\mathbb {C}}}$
-linear combination of the
$\operatorname {{\mathbb {C}}}$
-linear combination of the
![]() $f_i$
, there must exist at least one
$f_i$
, there must exist at least one
![]() $f = f_{i^*}$
which has multiplicity precisely one along D. Then f is a local defining equation for D, that is,
$f = f_{i^*}$
which has multiplicity precisely one along D. Then f is a local defining equation for D, that is,
![]() $f|_y = f_{i^*}|_y$
generates
$f|_y = f_{i^*}|_y$
generates
![]() $\mathcal {O}_X(-D)|_y$
. In particular, the weight of the action of T on
$\mathcal {O}_X(-D)|_y$
. In particular, the weight of the action of T on
![]() $\mathcal {O}_X(-D)|_y$
is
$\mathcal {O}_X(-D)|_y$
is
![]() $\mu _{i^*}$
. Thus,
$\mu _{i^*}$
. Thus,
![]() $\mu = \mu _{i^*}$
, thereby proving (3.2).
$\mu = \mu _{i^*}$
, thereby proving (3.2).
Now, it follows from Luna’s étale slice theorem, cf. for example [Reference Milne24, Lemma 13.36], that
for some formal functions
![]() $z_i$
satisfying
$z_i$
satisfying ![]() for any
for any
![]() $i = 1, \ldots n$
. Express
$i = 1, \ldots n$
. Express

as a formal power series. Since ![]() by (3.2), it follows that
by (3.2), it follows that
![]() $a_J = 0$
for all but possibly those
$a_J = 0$
for all but possibly those
![]() $J = (m_1, \ldots , m_n)$
such that
$J = (m_1, \ldots , m_n)$
such that
![]() $\sum m_i \cdot \nu _i = \mu $
. As
$\sum m_i \cdot \nu _i = \mu $
. As
![]() $f \neq 0$
, we deduce that there exists at least one
$f \neq 0$
, we deduce that there exists at least one ![]() such that
such that
![]() $\mu = \sum _i m_i \cdot \nu _i$
. This proves the assertion.
$\mu = \sum _i m_i \cdot \nu _i$
. This proves the assertion.
Finally, if
![]() $y\notin D$
we may take
$y\notin D$
we may take
![]() $f = 1$
, the constant function. As
$f = 1$
, the constant function. As ![]() we conclude that T acts trivially on
we conclude that T acts trivially on
![]() $\mathcal {O}_X(-D)|_y$
as proclaimed.
$\mathcal {O}_X(-D)|_y$
as proclaimed.
Moreover, if
![]() $y\in D$
is a smooth point of D then
$y\in D$
is a smooth point of D then
![]() $\mathcal {N}^*_{D/X}|_y \subseteq \Omega ^1_{X}|_y$
is a one-dimensional subspace, generated by
$\mathcal {N}^*_{D/X}|_y \subseteq \Omega ^1_{X}|_y$
is a one-dimensional subspace, generated by
![]() $df|_y$
. We compute
$df|_y$
. We compute
Thus the weights of the actions of T on
![]() $\mathcal {O}_X(-D)|_y$
and
$\mathcal {O}_X(-D)|_y$
and
![]() $\mathcal {N}^*_{D/X}|_{y}$
are the same and we are done.
$\mathcal {N}^*_{D/X}|_{y}$
are the same and we are done.
The presence of the divisor A in the following Lemma should be understood to be of a purely technical nature. Note that in any case Lemma 3.18 is no more general than Theorem C as also the pair
![]() $(X, D - A)$
is sub-log canonical, see [Reference Kollár and Mori18, Corollary 2.35].
$(X, D - A)$
is sub-log canonical, see [Reference Kollár and Mori18, Corollary 2.35].
Lemma 3.18. Let
![]() $(X, D)$
be a projective, log smooth, sub-log canonical pair and fix an algebraic torus
$(X, D)$
be a projective, log smooth, sub-log canonical pair and fix an algebraic torus
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X, D)$
. Let
$T\subseteq \operatorname {\mathrm {Aut}}(X, D)$
. Let
![]() $A \geq 0$
be an effective, T-invariant
$A \geq 0$
be an effective, T-invariant ![]() -divisor.
-divisor.
If
![]() $-(K_X+ D - A)$
is ample, then
$-(K_X+ D - A)$
is ample, then
![]() $0 \in P_{\mu }(X, -(K_X+ D - A))$
.
$0 \in P_{\mu }(X, -(K_X+ D - A))$
.
Remark 3.19. Note that in view of item
![]() $(1)$
in Proposition 3.13 it makes sense to define the moment polytope
$(1)$
in Proposition 3.13 it makes sense to define the moment polytope
![]() $P_{\mu }(X, -(K_X+ D - A))$
even if
$P_{\mu }(X, -(K_X+ D - A))$
even if
![]() $A, D$
are only
$A, D$
are only
![]() $\operatorname {{\mathbb {Q}}}$
-divisors by choosing m such that
$\operatorname {{\mathbb {Q}}}$
-divisors by choosing m such that
![]() $-m(K_X+ D - A)$
is Cartier and setting
$-m(K_X+ D - A)$
is Cartier and setting
Proof of Lemma 3.18
Choose
![]() $y\in X^T\neq \emptyset $
and let us denote by
$y\in X^T\neq \emptyset $
and let us denote by ![]() the weight of the action of T on
the weight of the action of T on
![]() $\mathcal {O}_X(-(K_X+ D - A))|_y$
Footnote
1
. Below, we will prove that
$\mathcal {O}_X(-(K_X+ D - A))|_y$
Footnote
1
. Below, we will prove that
for all sufficiently small
![]() $\varepsilon \geq 0$
. Using some completely elementary convex geometry this immediately yields the result, cf. Proposition 3.20 below.
$\varepsilon \geq 0$
. Using some completely elementary convex geometry this immediately yields the result, cf. Proposition 3.20 below.
To this end, let us denote the weights of the action of T on
![]() $\Omega _X^1|_{y}$
by
$\Omega _X^1|_{y}$
by
![]() $\nu _1, \ldots , \nu _n$
. As D has SNC-support, we may write
$\nu _1, \ldots , \nu _n$
. As D has SNC-support, we may write
 $$ \begin{align*} D = \sum_{i=1}^{s} \delta_i D_i \end{align*} $$
$$ \begin{align*} D = \sum_{i=1}^{s} \delta_i D_i \end{align*} $$
in some analytic open neighbourhood of
![]() $y\in X$
so that the
$y\in X$
so that the
![]() $D_i$
are smooth divisors meeting transversely at y and where
$D_i$
are smooth divisors meeting transversely at y and where
![]() $s\leq n$
. Then the
$s\leq n$
. Then the
![]() $\mathcal {N}^*_{D_i/X}|_{y}\subseteq \Omega _X^1|_{y}$
are distinct, one-dimensional, T-invariant subspaces. In particular, by Proposition 3.17 and after possibly re-indexing the
$\mathcal {N}^*_{D_i/X}|_{y}\subseteq \Omega _X^1|_{y}$
are distinct, one-dimensional, T-invariant subspaces. In particular, by Proposition 3.17 and after possibly re-indexing the
![]() $D_i$
, we may assume that for any
$D_i$
, we may assume that for any
![]() $i=1, \ldots , s$
the weight of the action of T on
$i=1, \ldots , s$
the weight of the action of T on
![]() $\mathcal {N}^*_{D_i/X}|_{y} \subseteq \Omega _X^1|_{y}$
is given by
$\mathcal {N}^*_{D_i/X}|_{y} \subseteq \Omega _X^1|_{y}$
is given by
![]() $\nu _i$
. Note that
$\nu _i$
. Note that
![]() $\delta _i\leq 1$
as
$\delta _i\leq 1$
as
![]() $(X, D)$
is assumed to be sub-log canonical. Let us set
$(X, D)$
is assumed to be sub-log canonical. Let us set
![]() $\delta _i = 0$
for
$\delta _i = 0$
for
![]() $s+1 \leq i \leq n$
. Write
$s+1 \leq i \leq n$
. Write
![]() $A = \sum a_j A_j$
, where, by assumption,
$A = \sum a_j A_j$
, where, by assumption,
![]() $a_j \geq 0$
for all j.
$a_j \geq 0$
for all j.
Then by Proposition 3.17 the weight
![]() $\mu $
of the action of T on
$\mu $
of the action of T on
![]() $\mathcal {O}_X(-(K_X+ D - A))|_y$
satisfies the following equation:
$\mathcal {O}_X(-(K_X+ D - A))|_y$
satisfies the following equation:

for some integers
![]() $m_{i, j} \geq 0$
.
$m_{i, j} \geq 0$
.
On the other hand, it is an important fact that if
![]() $\mathscr {L}$
is any T-linearized ample line bundle on X anf if
$\mathscr {L}$
is any T-linearized ample line bundle on X anf if
![]() $\mu $
denotes the weight of the action of T on
$\mu $
denotes the weight of the action of T on
![]() $\mathscr {L}|_y$
then
$\mathscr {L}|_y$
then
for sufficiently small
![]() $\varepsilon \geq 0$
, see [Reference Buczyński and Wiśniewski4, Corollary 2.14] for a quick and purely algebraic proofFootnote
2
.
$\varepsilon \geq 0$
, see [Reference Buczyński and Wiśniewski4, Corollary 2.14] for a quick and purely algebraic proofFootnote
2
.

Figure 1 Locally around the vertex
![]() $\mu $
the moment polytope
$\mu $
the moment polytope
![]() $P_\mu $
(drawn in blue) looks like the cone spanned by the weights of the action on the cotangent space (drawn in lilac).
$P_\mu $
(drawn in blue) looks like the cone spanned by the weights of the action on the cotangent space (drawn in lilac).
In any case in view of (3.4) and (3.5) we see that
 $$ \begin{align} (1-\varepsilon) \mu = \mu + \varepsilon \left( \sum_{i=1}^{n} (1-\delta_i) \nu_i + \sum_{i, j} a_j m_{j,i}\cdot \nu_{i} \right) \in P_{\mu}\Big(X, \mathcal{O}_X\big({-}(K_X+ D - A)\big)\Big), \end{align} $$
$$ \begin{align} (1-\varepsilon) \mu = \mu + \varepsilon \left( \sum_{i=1}^{n} (1-\delta_i) \nu_i + \sum_{i, j} a_j m_{j,i}\cdot \nu_{i} \right) \in P_{\mu}\Big(X, \mathcal{O}_X\big({-}(K_X+ D - A)\big)\Big), \end{align} $$
where we use that
![]() $\delta _i\leq 1$
as
$\delta _i\leq 1$
as
![]() $(X, D)$
is sub-log canonical and
$(X, D)$
is sub-log canonical and
![]() $a_j \geq 0$
as A is effective. This proves (3.3) as required. Finally, as was indicated already above, the claimed Lemma 3.18 now follows immediately from (3.3) and the following elementary consideration:
$a_j \geq 0$
as A is effective. This proves (3.3) as required. Finally, as was indicated already above, the claimed Lemma 3.18 now follows immediately from (3.3) and the following elementary consideration:
Proposition 3.20. Let V be a finite dimensional real vector space, let
![]() $W\subseteq V$
be a finite subset and let
$W\subseteq V$
be a finite subset and let
![]() $P\subseteq V$
be its convex hull. Assume that for any
$P\subseteq V$
be its convex hull. Assume that for any
![]() $w\in W$
it holds that
$w\in W$
it holds that
![]() $(1-\varepsilon )w \in P$
for all sufficiently small
$(1-\varepsilon )w \in P$
for all sufficiently small
![]() $0\leq \varepsilon $
. Then
$0\leq \varepsilon $
. Then
![]() $0\in P$
.
$0\in P$
.
Proof. Let us assume that
![]() $0\notin P$
. Then there exists a linear functional
$0\notin P$
. Then there exists a linear functional
![]() $\varphi $
on V such that
$\varphi $
on V such that
![]() $\varphi |_P> 0$
. As
$\varphi |_P> 0$
. As
![]() $P\subseteq V$
is compact and convex so is
$P\subseteq V$
is compact and convex so is
![]() $\varphi (P)\subseteq \operatorname {{\mathbb {R}}}$
, that is, it is a (compact) interval, say
$\varphi (P)\subseteq \operatorname {{\mathbb {R}}}$
, that is, it is a (compact) interval, say
![]() $\varphi (P) = [a,b]$
. Note that as P is the convex hull of W,
$\varphi (P) = [a,b]$
. Note that as P is the convex hull of W,
![]() $\varphi (P)$
is the convex hull of
$\varphi (P)$
is the convex hull of
![]() $\varphi (W)$
and so there exists at least one
$\varphi (W)$
and so there exists at least one
![]() $w\in W$
for which
$w\in W$
for which
![]() $\varphi (w) = a$
. But then our assumption that
$\varphi (w) = a$
. But then our assumption that
![]() $(1-\varepsilon )w \in P$
for all sufficiently small
$(1-\varepsilon )w \in P$
for all sufficiently small
![]() $0<\varepsilon $
contradicts the fact that
$0<\varepsilon $
contradicts the fact that
This completes the proof of the proposition.
Corollary 3.21. Let
![]() $(X, D)$
be a projective, log smooth, log canonical pair and fix an algebraic torus
$(X, D)$
be a projective, log smooth, log canonical pair and fix an algebraic torus
![]() $T\subseteq \operatorname {\mathrm {Aut}}(X, D)$
. If
$T\subseteq \operatorname {\mathrm {Aut}}(X, D)$
. If
![]() $-(K_X+ D)$
is nef, then
$-(K_X+ D)$
is nef, then
![]() $0 \in P_{\mu }(X, -(K_X+ D))$
.
$0 \in P_{\mu }(X, -(K_X+ D))$
.
Proof. Let us start by proving the following:
Claim. There exists a T-invariant, effective, ample divisor A on X.
Indeed, let
![]() $\mathscr {L}$
be a very ample line bundle on X. Then
$\mathscr {L}$
be a very ample line bundle on X. Then
![]() $\mathscr {L}$
is T-invariant and, possibly replacing
$\mathscr {L}$
is T-invariant and, possibly replacing
![]() $\mathscr {L}$
by some multiple, even linearizable, see [Reference Brion3, Theorem 5.2.1]. Let us choose an eigenvector
$\mathscr {L}$
by some multiple, even linearizable, see [Reference Brion3, Theorem 5.2.1]. Let us choose an eigenvector
![]() $\sigma \in \mathrm {H}^0(X, \mathscr {L})$
for the action of T of weight
$\sigma \in \mathrm {H}^0(X, \mathscr {L})$
for the action of T of weight
![]() $w \in M$
. Then the zero-set
$w \in M$
. Then the zero-set
![]() $A := Z(\sigma )$
is a T-invariant, effective, ample divisor on X as required.
$A := Z(\sigma )$
is a T-invariant, effective, ample divisor on X as required.
Now, write
![]() $A = \sum _j a_j A_j$
as the sum of distinct prime divisors. For any rational number
$A = \sum _j a_j A_j$
as the sum of distinct prime divisors. For any rational number
![]() $\varepsilon> 0$
we consider the ample (!) divisor
$\varepsilon> 0$
we consider the ample (!) divisor
According to Lemma 3.18 it holds that
We are now ready to conclude that
![]() $0 \in P := P_0 := P_{\mu }(X, -(K_X+ D))$
: Let us denote by
$0 \in P := P_0 := P_{\mu }(X, -(K_X+ D))$
: Let us denote by
the Hausdorff distance between
![]() $P_\varepsilon $
and P with respect to some norm on
$P_\varepsilon $
and P with respect to some norm on ![]() . Note that by definition and for any
. Note that by definition and for any
![]() $\varepsilon \geq 0$
, the polytope
$\varepsilon \geq 0$
, the polytope
![]() $P_{\varepsilon }$
is the convex hull of the weights
$P_{\varepsilon }$
is the convex hull of the weights
![]() $\mu _{\varepsilon , k}$
of the action of T on
$\mu _{\varepsilon , k}$
of the action of T on
![]() $ \mathcal {O}_X(-(K_X+ D - \varepsilon A))|_{y_k}$
. Moreover, by (3.4) we have
$ \mathcal {O}_X(-(K_X+ D - \varepsilon A))|_{y_k}$
. Moreover, by (3.4) we have
 $$ \begin{align*} \mu_{0, k} = \mu_{\varepsilon, k} + \varepsilon \left( \sum_{i, j} a_{j} m^{(k)}_{j, i} \cdot \nu_{i} \right) \end{align*} $$
$$ \begin{align*} \mu_{0, k} = \mu_{\varepsilon, k} + \varepsilon \left( \sum_{i, j} a_{j} m^{(k)}_{j, i} \cdot \nu_{i} \right) \end{align*} $$
for some integers
![]() $m^{(k)}_{j, i} \geq 0$
, depending only on the weights of the action of T on
$m^{(k)}_{j, i} \geq 0$
, depending only on the weights of the action of T on
![]() $\mathcal {O}_X(-A_j)|_{y_k}$
but not on
$\mathcal {O}_X(-A_j)|_{y_k}$
but not on
![]() $\varepsilon \geq 0$
, cf. Proposition 3.17. We infer that clearly
$\varepsilon \geq 0$
, cf. Proposition 3.17. We infer that clearly
![]() $d(P_\varepsilon , P_0)\rightarrow 0$
as
$d(P_\varepsilon , P_0)\rightarrow 0$
as
![]() $\varepsilon \rightarrow 0$
. In particular,
$\varepsilon \rightarrow 0$
. In particular,
![]() $d(P_0, 0) \leq d(P_\varepsilon , P_0)\rightarrow 0$
and so
$d(P_0, 0) \leq d(P_\varepsilon , P_0)\rightarrow 0$
and so
![]() $0\in P = P_0$
, using that the latter set is closed.
$0\in P = P_0$
, using that the latter set is closed.
The rest of this section is devoted to giving examples which demonstrate that the assumptions in Theorem 3.1, and hence in Theorem C, are essentially optimal.
Example 3.22. The conclusion of Theorem 3.1 fails if we allow for more general subgroups
![]() $H \subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
. In fact, the following example shows that it is already wrong for solvable groups:
$H \subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
. In fact, the following example shows that it is already wrong for solvable groups:
Let
![]() $X = \operatorname {{\mathbb {P}}}^1$
,
$X = \operatorname {{\mathbb {P}}}^1$
,
![]() $D = 0$
and let
$D = 0$
and let ![]() be the group of diagonal matrices as before. Then one easily checks that
be the group of diagonal matrices as before. Then one easily checks that
 $$ \begin{align*} \bigoplus_{m= 0}^\infty H^0(X, \mathcal{O}_X(-mK_X))^T = \operatorname{{\mathbb{C}}}[z \partial_z] \end{align*} $$
$$ \begin{align*} \bigoplus_{m= 0}^\infty H^0(X, \mathcal{O}_X(-mK_X))^T = \operatorname{{\mathbb{C}}}[z \partial_z] \end{align*} $$
is generated by a single section. However, the vector field
![]() $z \partial _z$
is not invariant under the action of the subgroup
$z \partial _z$
is not invariant under the action of the subgroup ![]() of upper triangular matrices.
of upper triangular matrices.
Example 3.23. The above example shows that usually
![]() $\kappa (X, -(K_X + D))^T$
is strictly smaller than
$\kappa (X, -(K_X + D))^T$
is strictly smaller than
![]() $\kappa (X, -(K_X + D))$
even when the assumptions in Theorem 3.1 are satisfied. In fact, it is straightforward to extend Example 3.22 to show that
$\kappa (X, -(K_X + D))$
even when the assumptions in Theorem 3.1 are satisfied. In fact, it is straightforward to extend Example 3.22 to show that
for any
![]() $n\geq 1$
. Here,
$n\geq 1$
. Here, ![]() denotes the torus of diagonal matrices.
denotes the torus of diagonal matrices.
Example 3.24. The assumption that
![]() $(X, D)$
is sub-log canonical is optimal as the following example demonstrates: Consider
$(X, D)$
is sub-log canonical is optimal as the following example demonstrates: Consider
![]() $X = \operatorname {{\mathbb {P}}}^1$
equipped with
$X = \operatorname {{\mathbb {P}}}^1$
equipped with
![]() $D = a\cdot \{0\}$
for some
$D = a\cdot \{0\}$
for some
![]() $a\in \operatorname {{\mathbb {Q}}}$
. Then the standard torus of diagonal matrices
$a\in \operatorname {{\mathbb {Q}}}$
. Then the standard torus of diagonal matrices
![]() $T \cong \operatorname {{\mathbb {C}}}^\times \subseteq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
acts on
$T \cong \operatorname {{\mathbb {C}}}^\times \subseteq \operatorname {\mathrm {Aut}}(\operatorname {{\mathbb {P}}}^1)$
acts on
![]() $\operatorname {{\mathbb {P}}}^1$
via
$\operatorname {{\mathbb {P}}}^1$
via ![]() . Note that the weight of the action of T on
. Note that the weight of the action of T on
![]() $\mathcal {T}_{\operatorname {{\mathbb {P}}}^1}|_0$
is given by
$\mathcal {T}_{\operatorname {{\mathbb {P}}}^1}|_0$
is given by
![]() $1\in \operatorname {{\mathbb {Z}}}\cong M$
and the weight of the action of T on
$1\in \operatorname {{\mathbb {Z}}}\cong M$
and the weight of the action of T on
![]() $\mathcal {T}_{\operatorname {{\mathbb {P}}}^1}|_\infty $
is given by
$\mathcal {T}_{\operatorname {{\mathbb {P}}}^1}|_\infty $
is given by
![]() $-1\in M$
. Consequently, the weights of the action of T on
$-1\in M$
. Consequently, the weights of the action of T on
![]() $\Omega ^1_{\operatorname {{\mathbb {P}}}^1}|_0$
and
$\Omega ^1_{\operatorname {{\mathbb {P}}}^1}|_0$
and
![]() $\Omega ^1_{\operatorname {{\mathbb {P}}}^1}|_\infty $
are given by
$\Omega ^1_{\operatorname {{\mathbb {P}}}^1}|_\infty $
are given by
![]() $-1$
and
$-1$
and
![]() $1,$
respectively. Thus,
$1,$
respectively. Thus,
![]() $P_{\mu }(\operatorname {{\mathbb {P}}}^1, \mathcal {O}(-K_{\operatorname {{\mathbb {P}}}^1})) = [-1, 1]$
and, hence, using Example 3.17
$P_{\mu }(\operatorname {{\mathbb {P}}}^1, \mathcal {O}(-K_{\operatorname {{\mathbb {P}}}^1})) = [-1, 1]$
and, hence, using Example 3.17
We conclude that
![]() $-(K_{\operatorname {{\mathbb {P}}}^1}+D)$
has T-invariant sections if and only if
$-(K_{\operatorname {{\mathbb {P}}}^1}+D)$
has T-invariant sections if and only if
![]() $a\leq 1$
which is the case if and only if
$a\leq 1$
which is the case if and only if
![]() $(X, D)$
is sub-log canonical. At the same time, notice that
$(X, D)$
is sub-log canonical. At the same time, notice that
![]() $-(K_{\operatorname {{\mathbb {P}}}^1}+D)$
is ample as long as
$-(K_{\operatorname {{\mathbb {P}}}^1}+D)$
is ample as long as
![]() $a\leq 2$
.
$a\leq 2$
.
4 Proof of the main results
4.1 Proof of Theorem C
Let
![]() $(X, D)$
be a projective, sub-log canonical pair and assume that
$(X, D)$
be a projective, sub-log canonical pair and assume that
![]() $-(K_X + D)$
is semiample. Fix a connected, commutative, linear algebraic subgroup
$-(K_X + D)$
is semiample. Fix a connected, commutative, linear algebraic subgroup
![]() $H\subseteq \operatorname {\mathrm {Aut}}(X, D)$
. We need to show that
$H\subseteq \operatorname {\mathrm {Aut}}(X, D)$
. We need to show that
If
![]() $(X, D)$
is log smooth, then this was already shown in Theorem 3.1, cf. also Lemma 2.3. In general, we choose an H-equivariant log resolution
$(X, D)$
is log smooth, then this was already shown in Theorem 3.1, cf. also Lemma 2.3. In general, we choose an H-equivariant log resolution
![]() $f\colon \hat {X} \rightarrow X$
of
$f\colon \hat {X} \rightarrow X$
of
![]() $(X, D)$
. Such a map always exists by [Reference Kollár19, Proposition 3.9.1]. Then, in particular
$(X, D)$
. Such a map always exists by [Reference Kollár19, Proposition 3.9.1]. Then, in particular ![]() will be H-invariant.
will be H-invariant.
Let us write
where
![]() $\hat {D}$
is supported on the strict transform of D and the exceptional locus of f. Then
$\hat {D}$
is supported on the strict transform of D and the exceptional locus of f. Then
![]() $(\hat {X}, \hat {D})$
is a log smooth pair which is sub-log canonical as
$(\hat {X}, \hat {D})$
is a log smooth pair which is sub-log canonical as
![]() $(X, D)$
is so, see [Reference Kollár and Mori18, Lemma 2.30]. Also, by construction,
$(X, D)$
is so, see [Reference Kollár and Mori18, Lemma 2.30]. Also, by construction,
is semiample. Thus the conditions in Theorem 3.1 are satisfied and we deduce that
Let us fix an integer
![]() $m\geq 1$
such that
$m\geq 1$
such that
![]() $-m(K_{\hat {X}} + \hat {D} )$
is Cartier and such that there exists an H-invariant form
$-m(K_{\hat {X}} + \hat {D} )$
is Cartier and such that there exists an H-invariant form
 $$ \begin{align*} \hat{\tau} \in \hspace{0.1cm }& H^0\Big(\widehat{X}, \mathcal{O}_{\widehat{X}}\Big({-}m\big(K_{\hat{X}} + \hat{D} \big)\Big)\Big)\\ \cong \hspace{0.1cm }& H^0\Big(\widehat{X}, \mathcal{O}_{\widehat{X}}\big(f^*({-}m(K_X + D))\big)\Big) \\ = \hspace{0.1cm }& H^0\big(X, \mathcal{O}_{X}\big({-}m(K_X + D)\big)\big). \end{align*} $$
$$ \begin{align*} \hat{\tau} \in \hspace{0.1cm }& H^0\Big(\widehat{X}, \mathcal{O}_{\widehat{X}}\Big({-}m\big(K_{\hat{X}} + \hat{D} \big)\Big)\Big)\\ \cong \hspace{0.1cm }& H^0\Big(\widehat{X}, \mathcal{O}_{\widehat{X}}\big(f^*({-}m(K_X + D))\big)\Big) \\ = \hspace{0.1cm }& H^0\big(X, \mathcal{O}_{X}\big({-}m(K_X + D)\big)\big). \end{align*} $$
Here, for the isomorphism in the second line we used (4.1). Let us denote by
![]() $\tau \in H^0(X, \mathcal {O}_{X}(-m(K_X + D)))$
the image of
$\tau \in H^0(X, \mathcal {O}_{X}(-m(K_X + D)))$
the image of
![]() $\hat {\tau }$
under this isomorphism. We claim that
$\hat {\tau }$
under this isomorphism. We claim that
![]() $\tau $
is H-invariant, concluding the proof of the Lemma. Note that this is not entirely clear as the natural H-actions on both sides may a priori differ.
$\tau $
is H-invariant, concluding the proof of the Lemma. Note that this is not entirely clear as the natural H-actions on both sides may a priori differ.
However, as
![]() $f\colon \hat {X} \rightarrow X$
is birational and H-equivariant, the set
$f\colon \hat {X} \rightarrow X$
is birational and H-equivariant, the set ![]() is a dense open H-invariant subset of
is a dense open H-invariant subset of
![]() $\hat {X}$
on which f is an isomorphism. In particular, we see that
$\hat {X}$
on which f is an isomorphism. In particular, we see that
As
![]() $\hat {\tau }$
is H-invariant we infer that so is
$\hat {\tau }$
is H-invariant we infer that so is
![]() $\hat {\tau }|_U = \tau |_U$
and, hence, (by continuity)
$\hat {\tau }|_U = \tau |_U$
and, hence, (by continuity)
![]() $\tau $
. Thus, we have produced a non-trivial H-invariant form
$\tau $
. Thus, we have produced a non-trivial H-invariant form
![]() $\tau \in H^0(X, \mathcal {O}_{X}(-m(K_X + D)))$
and we are done.
$\tau \in H^0(X, \mathcal {O}_{X}(-m(K_X + D)))$
and we are done.
4.3 Proof of Corollary B
Let
![]() $(X, \Delta )$
a projective klt threefold pair with nef anti-log canonical divisor
$(X, \Delta )$
a projective klt threefold pair with nef anti-log canonical divisor
![]() $-(K_X+\Delta )$
. We want to prove that
$-(K_X+\Delta )$
. We want to prove that
Let us start with some preliminary considerations. Let us denote by
![]() $(F, \Delta _F)$
a general fibre of the MRC fibration of
$(F, \Delta _F)$
a general fibre of the MRC fibration of
![]() $(X, \Delta )$
as in Theorem 2.1. Then F is a rationally connnected projective variety,
$(X, \Delta )$
as in Theorem 2.1. Then F is a rationally connnected projective variety,
![]() $(F, \Delta _F)$
is a klt pair and
$(F, \Delta _F)$
is a klt pair and
![]() $-(K_F + \Delta _F)$
is nef. We distinguish four cases according to whether
$-(K_F + \Delta _F)$
is nef. We distinguish four cases according to whether
![]() $\dim F = 0,1,2,3$
.
$\dim F = 0,1,2,3$
.
If
![]() $\dim F = 3$
, then
$\dim F = 3$
, then
![]() $X=F$
and (4.2) follows from [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21, Theorem A]. In the other cases, according to Theorem 2.2 we need to prove that for any algebraic torus
$X=F$
and (4.2) follows from [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21, Theorem A]. In the other cases, according to Theorem 2.2 we need to prove that for any algebraic torus
![]() $T\subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
it holds that
$T\subseteq \operatorname {\mathrm {Aut}}(F, \Delta _F)$
it holds that
In case
![]() $\dim F = 0$
, if
$\dim F = 0$
, if
![]() $F = \{ * \}$
is a point, there is nothing to prove, cf. Theorem 2.1. Also the case
$F = \{ * \}$
is a point, there is nothing to prove, cf. Theorem 2.1. Also the case
![]() $\dim F = 1$
is easy to settle, for example because in this case clearly
$\dim F = 1$
is easy to settle, for example because in this case clearly
![]() $F= \operatorname {{\mathbb {P}}}^1$
. Then since
$F= \operatorname {{\mathbb {P}}}^1$
. Then since
![]() $-(K_F + \Delta _F)$
is nef it is even semiample and (4.2) is a direct consequence of Theorem A. Thus, it remains to deal with the case when F is a surface.
$-(K_F + \Delta _F)$
is nef it is even semiample and (4.2) is a direct consequence of Theorem A. Thus, it remains to deal with the case when F is a surface.
So let us then assume that F is a surface. If
![]() $T = \{1\}$
is trivial, then we simply need to verify that
$T = \{1\}$
is trivial, then we simply need to verify that
which was proved in [Reference Han and Liu14, Theorem 1.5]. Alternatively, this statement is also contained in [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21, Theorem A]. In any case, note that this is precisely the situation when
![]() $X = Y \times F$
is a product.
$X = Y \times F$
is a product.
It remains to deal with the case that
![]() $\dim T \geq 1$
. Proceeding exactly as in the proof of Theorem C we may replace F by a log resolution. Note that this may force us to allow for
$\dim T \geq 1$
. Proceeding exactly as in the proof of Theorem C we may replace F by a log resolution. Note that this may force us to allow for
![]() $(F, \Delta _F)$
to be only sub-klt but this will not be an issue henceforth. In any case, we may assume F to be smooth.
$(F, \Delta _F)$
to be only sub-klt but this will not be an issue henceforth. In any case, we may assume F to be smooth.
Now, as
![]() $\dim T \geq 1$
, the surface F is certainly a T-variety of complexity one, a variety equipped with the action of an algebraic torus such that the maximal dimensional orbits have codimension one in F. But then F is an Mori Dream Space in the sense of [Reference Hu and Keel16], so that
$\dim T \geq 1$
, the surface F is certainly a T-variety of complexity one, a variety equipped with the action of an algebraic torus such that the maximal dimensional orbits have codimension one in F. But then F is an Mori Dream Space in the sense of [Reference Hu and Keel16], so that
![]() $-(K_F + \Delta _F)$
is not only nef but also semiample. Hence, (4.2) follows from Theorem C.
$-(K_F + \Delta _F)$
is not only nef but also semiample. Hence, (4.2) follows from Theorem C.
The assertion that F is a Mori Dream Space under the above hypothesis seems to be well-known, for the convenience of the reader we nevertheless provide a detailed explanation below: As F is a smooth, rationally connected surface, it is in particular rational, birational to ![]() . It follows that the class group
. It follows that the class group
![]() $\mathrm {Cl}(F)$
is finitely generated. Thus, to prove that F is a Mori Dream Space it only remains to show that the Cox ring of F is finitely generated, see [Reference Hu and Keel16, Proposition 2.9]. But indeed, Hausen and Süß in [Reference Hausen and Süß15, Theorem 1.3] can even determine an explicit finite list of generators and relations in terms of combinatorial data associated to the T-action. The theorem is proved.
$\mathrm {Cl}(F)$
is finitely generated. Thus, to prove that F is a Mori Dream Space it only remains to show that the Cox ring of F is finitely generated, see [Reference Hu and Keel16, Proposition 2.9]. But indeed, Hausen and Süß in [Reference Hausen and Süß15, Theorem 1.3] can even determine an explicit finite list of generators and relations in terms of combinatorial data associated to the T-action. The theorem is proved.
Acknowledgements
First and foremost, the author would like to express his sincere gratitude towards Jarosław Wiśniewski for sketching to the author the proof of Theorem C in the case of a smooth Fanos without boundary. This paper would not exist without him. The author would also like to take this opportunity to warmly thank Roland Púček and Andriy Regeta for organising the “Regional Workshop in Algebraic Geometry” at Jena where the author and Jarosław Wiśniewski met.
Second, the author is extremely grateful towards the authors of [Reference Lazić, Matsumura, Peternell, Tsakanikas and Xie21] for bringing up the question whether Theorem A is true and, in particular, Shin-Ichi Matsumura and Thomas Peternell for several inspiring and fruitful initial discussions on the issue. Moreover, he is indebted to Vladimir Lazić and to Nikolaos Tsakanikas for many helpful comments on an early draft of this text and especially to Nikolaos Tsakanikas and Lingyao Xie for pointing out a serious mistake in an earlier version of this text.
He would also like to thank Daniel Greb for his advice and for always trying to make the author see the positive side of things, and Jochen Heinloth for several helpful discussions on torus-actions and for always being glad to answer any question of anyone stumbling by his office. Finally, he would like to warmly thank the anonymous referee for their detailed review and their valuable suggestions.
The author gladly wants to acknowledge that while writing this article he was supported from the DFG Research Training Group 2553 ”Symmetries and Classifying Spaces: Analytic, Arithmetic, and Derived.