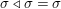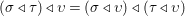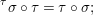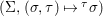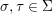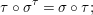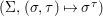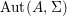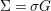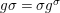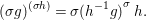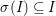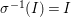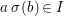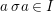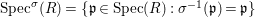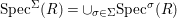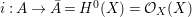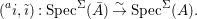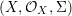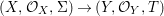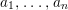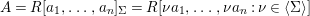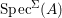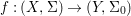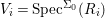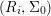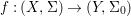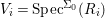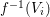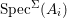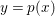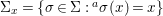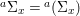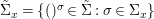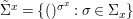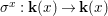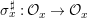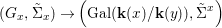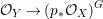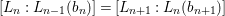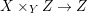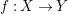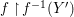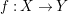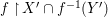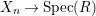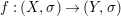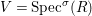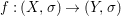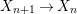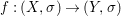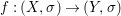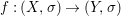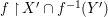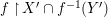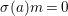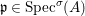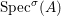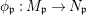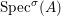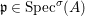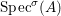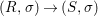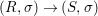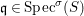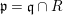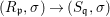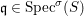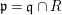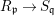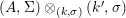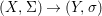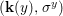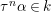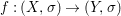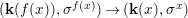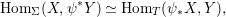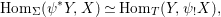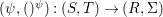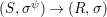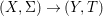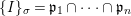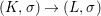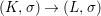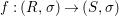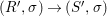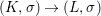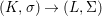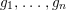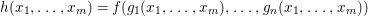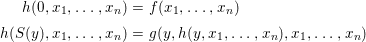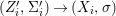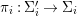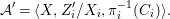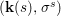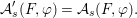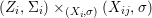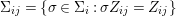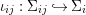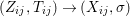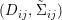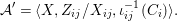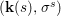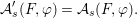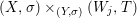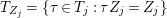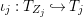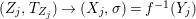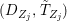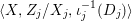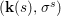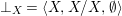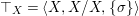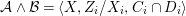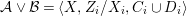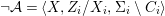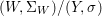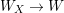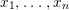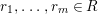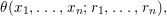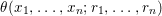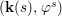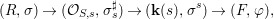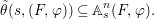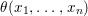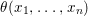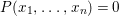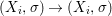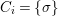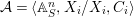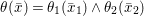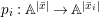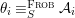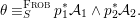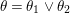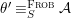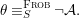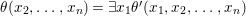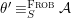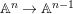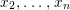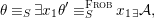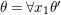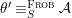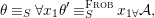1 Introduction
Galois stratification, originally developed through work of Fried, Haran, Jarden and Sacerdote [Reference Fried and Jarden13], [Reference Fried and Sacerdote14], [Reference Fried, Haran and Jarden12], provides an explicit arithmetic–geometric description of definable sets over finite fields in terms of Galois formulas associated to Galois covers of algebraic varieties. When compared to the earlier work of Ax [Reference Ax2], made more explicit by Kiefe [Reference Kiefe19], which showed that every formula in the language of rings is equivalent to a formula with a single (bounded) existential quantifier, the fundamental achievement of the Galois stratification was the effective (in fact primitive recursive) nature of its quantifier elimination procedure. Moreover, the precise description of formulas in terms of Galois covers was particularly well suited for applications of geometric and number-theoretic nature, for example in Fried’s work on Davenport’s problem [Reference Fried11]. In our opinion, the most impressive application was in the work of Denef and Loeser on arithmetic motivic integration in [Reference Denef and Loeser8]. They assign a Chow motive to a Galois formula, thus extending the consideration of algebraic–geometric invariants of algebraic varieties to arbitrary first-order formulas.
We develop the theory of twisted Galois stratification in order to describe first-order definable sets in the language of difference rings over algebraic closures of finite fields equipped with powers of the Frobenius automorphism. A (normal) Galois stratification on a difference scheme ![]() $(X,{\it\sigma})$ is a datum
$(X,{\it\sigma})$ is a datum
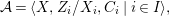 $$\begin{eqnarray}{\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\mid i\in I\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\mid i\in I\rangle ,\end{eqnarray}$$ where ![]() $X_{i}$,
$X_{i}$, ![]() $i\in I$ is a partition of
$i\in I$ is a partition of ![]() $X$ into finitely many normal locally closed difference subschemes of
$X$ into finitely many normal locally closed difference subschemes of ![]() $X$, each
$X$, each 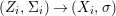 $(Z_{i},{\rm\Sigma}_{i})\rightarrow (X_{i},{\it\sigma})$ is a Galois cover with some group
$(Z_{i},{\rm\Sigma}_{i})\rightarrow (X_{i},{\it\sigma})$ is a Galois cover with some group 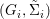 $(G_{i},\tilde{{\rm\Sigma}}_{i})$ and
$(G_{i},\tilde{{\rm\Sigma}}_{i})$ and ![]() $C_{i}$ is a conjugacy domain in
$C_{i}$ is a conjugacy domain in ![]() ${\rm\Sigma}_{i}$, with all these notions defined in Section 2. The Galois formula associated with
${\rm\Sigma}_{i}$, with all these notions defined in Section 2. The Galois formula associated with ![]() ${\mathcal{A}}$ is the realization subfunctor
${\mathcal{A}}$ is the realization subfunctor ![]() $\tilde{{\mathcal{A}}}$ of
$\tilde{{\mathcal{A}}}$ of ![]() $X$ defined by the assignment
$X$ defined by the assignment
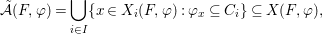 $$\begin{eqnarray}\tilde{{\mathcal{A}}}(F,{\it\varphi})=\mathop{\bigcup }_{i\in I}\{x\in X_{i}(F,{\it\varphi}):{\it\varphi}_{x}\subseteq C_{i}\}\subseteq X(F,{\it\varphi}),\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{A}}}(F,{\it\varphi})=\mathop{\bigcup }_{i\in I}\{x\in X_{i}(F,{\it\varphi}):{\it\varphi}_{x}\subseteq C_{i}\}\subseteq X(F,{\it\varphi}),\end{eqnarray}$$ where ![]() $(F,{\it\varphi})$ is an algebraically closed difference field and the conjugacy class
$(F,{\it\varphi})$ is an algebraically closed difference field and the conjugacy class ![]() ${\it\varphi}_{x}\subseteq {\rm\Sigma}$ is the local
${\it\varphi}_{x}\subseteq {\rm\Sigma}$ is the local ![]() ${\it\varphi}$-substitution at
${\it\varphi}$-substitution at ![]() $x$ (see 3.44). Our principal result in its algebraic–geometric incarnation is the following direct image theorem, stating that a direct image of a Galois formula by a morphism of finite transformal type is equivalent to a Galois formula over fields with Frobenii. Equivalently, the class of Galois formulas over fields with Frobenii is closed under taking direct images by morphisms of finite transformal type (the precise statement is 7.12).
$x$ (see 3.44). Our principal result in its algebraic–geometric incarnation is the following direct image theorem, stating that a direct image of a Galois formula by a morphism of finite transformal type is equivalent to a Galois formula over fields with Frobenii. Equivalently, the class of Galois formulas over fields with Frobenii is closed under taking direct images by morphisms of finite transformal type (the precise statement is 7.12).
Theorem 1.1. Let 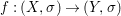 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of finite transformal type (over a suitable base), and let
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of finite transformal type (over a suitable base), and let ![]() ${\mathcal{A}}$ be a Galois stratification on
${\mathcal{A}}$ be a Galois stratification on ![]() $X$. We can effectively compute a Galois stratification
$X$. We can effectively compute a Galois stratification ![]() ${\mathcal{B}}$ on
${\mathcal{B}}$ on ![]() $Y$ such that for all (suitable)
$Y$ such that for all (suitable) ![]() $(\bar{\mathbb{F}}_{p},{\it\varphi})$ with a high enough power of Frobenius
$(\bar{\mathbb{F}}_{p},{\it\varphi})$ with a high enough power of Frobenius ![]() ${\it\varphi}$,
${\it\varphi}$,
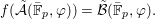 $$\begin{eqnarray}f(\tilde{{\mathcal{A}}}(\bar{\mathbb{F}}_{p},{\it\varphi}))=\tilde{{\mathcal{B}}}(\bar{\mathbb{F}}_{p},{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}f(\tilde{{\mathcal{A}}}(\bar{\mathbb{F}}_{p},{\it\varphi}))=\tilde{{\mathcal{B}}}(\bar{\mathbb{F}}_{p},{\it\varphi}).\end{eqnarray}$$A model-theoretic restatement of the above theorem is that fields with Frobenii allow quantifier elimination in the language of Galois formulas. In other words, any definable set over fields with powers of Frobenius can be described by a Galois formula (the precise statement is 7.15).
Theorem 1.2. Let 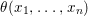 ${\it\theta}(x_{1},\ldots ,x_{n})$ be a first-order formula in the language of difference rings (with suitable parameters). We can effectively compute a Galois stratification
${\it\theta}(x_{1},\ldots ,x_{n})$ be a first-order formula in the language of difference rings (with suitable parameters). We can effectively compute a Galois stratification ![]() ${\mathcal{A}}$ of the difference affine
${\mathcal{A}}$ of the difference affine ![]() $n$-space such that for all (suitable)
$n$-space such that for all (suitable) ![]() $(\bar{\mathbb{F}}_{p},{\it\varphi})$ with a high enough power of Frobenius
$(\bar{\mathbb{F}}_{p},{\it\varphi})$ with a high enough power of Frobenius ![]() ${\it\varphi}$,
${\it\varphi}$,
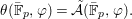 $$\begin{eqnarray}{\it\theta}(\bar{\mathbb{F}}_{p},{\it\varphi})=\tilde{{\mathcal{A}}}(\bar{\mathbb{F}}_{p},{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}(\bar{\mathbb{F}}_{p},{\it\varphi})=\tilde{{\mathcal{A}}}(\bar{\mathbb{F}}_{p},{\it\varphi}).\end{eqnarray}$$Conversely, every Galois formula is equivalent to a first-order formula in the language of difference rings over algebraically closed difference fields.
Historically speaking, the comparison of our result to the known model-theoretic quantifier elimination result found by Macintyre [Reference Macintyre21] and greatly refined in modern terms by Chatzidakis and Hrushovski [Reference Chatzidakis and Hrushovski6], is parallel to the relation between the work of Fried–Sacerdote and the work of Ax mentioned above. The logic quantifier elimination [Reference Chatzidakis and Hrushovski6, 1.6] states that any formula 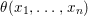 ${\it\theta}(x_{1},\ldots ,x_{n})$ in the language of difference rings is equivalent, modulo the theory ACFA of existentially closed difference fields, to a Boolean combination of formulas of the form
${\it\theta}(x_{1},\ldots ,x_{n})$ in the language of difference rings is equivalent, modulo the theory ACFA of existentially closed difference fields, to a Boolean combination of formulas of the form
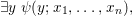 $$\begin{eqnarray}\exists y~{\it\psi}(y;x_{1},\ldots ,x_{n}),\end{eqnarray}$$
$$\begin{eqnarray}\exists y~{\it\psi}(y;x_{1},\ldots ,x_{n}),\end{eqnarray}$$ where ![]() ${\it\psi}$ is quantifier free, and
${\it\psi}$ is quantifier free, and 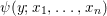 ${\it\psi}(y;x_{1},\ldots ,x_{n})$ implies that
${\it\psi}(y;x_{1},\ldots ,x_{n})$ implies that ![]() $y$ satisfies a nonzero polynomial whose coefficients are
$y$ satisfies a nonzero polynomial whose coefficients are ![]() ${\it\sigma}$-polynomials in
${\it\sigma}$-polynomials in 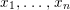 $x_{1},\ldots ,x_{n}$, that is, the single existential quantifier is bounded. The proof uses the compactness theorem and, although recursive, such quantifier elimination proceeds by unbounded searches and it is far from being primitive recursive or effective in a suitable sense of the word.
$x_{1},\ldots ,x_{n}$, that is, the single existential quantifier is bounded. The proof uses the compactness theorem and, although recursive, such quantifier elimination proceeds by unbounded searches and it is far from being primitive recursive or effective in a suitable sense of the word.
The main achievements of our paper are:
(1) the fine quantifier elimination, our Galois formulas being associated with finite Galois covers of difference schemes, whereas the covers associated with the logic quantifier elimination are in general only quasifinite, with possibly infinite algebraic extensions of function fields;
(2) the effectivity of our quantifier elimination procedure, the proof of the direct image theorem being fundamentally algorithmic and algebraic–geometric in nature.
We show that our quantifier elimination and the decision procedure for fields with Frobenii are ![]() $\dagger$-primitive recursive, that is, primitive recursive reducible to basic operations in difference algebraic geometry, as detailed in Section 6. Given that some of the most elementary constructions in difference algebra are not known to be primitive recursive themselves, the strength of the hybrid notion of
$\dagger$-primitive recursive, that is, primitive recursive reducible to basic operations in difference algebraic geometry, as detailed in Section 6. Given that some of the most elementary constructions in difference algebra are not known to be primitive recursive themselves, the strength of the hybrid notion of ![]() $\dagger$-primitive recursiveness is strongly dependent on future developments in the field of effective/constructive difference algebra. For that reason, we developed a coarser theory of direct Galois stratification (in the sense of 3.10), to show that the logic quantifier elimination is outright primitive recursive in [Reference Tomašić23]. Needless to say, while it may be possible to start with the model-theoretic quantifier elimination and deduce the precise form of 1.2 (in fact 7.17), taking this route would be missing the point.
$\dagger$-primitive recursiveness is strongly dependent on future developments in the field of effective/constructive difference algebra. For that reason, we developed a coarser theory of direct Galois stratification (in the sense of 3.10), to show that the logic quantifier elimination is outright primitive recursive in [Reference Tomašić23]. Needless to say, while it may be possible to start with the model-theoretic quantifier elimination and deduce the precise form of 1.2 (in fact 7.17), taking this route would be missing the point.
The statement 1.2 is over fields with Frobenii and that is why we must refer to the present author’s Chebotarev Lemma [Reference Tomašić24, 4.28] which uses the difficult paper [Reference Hrushovski18] on twisted Lang–Weil estimates, proving the earlier conjecture of [Reference Macintyre21] that ACFA is the elementary theory of fields with Frobenii. This is the only use of the main result of [Reference Hrushovski18] in this paper, and the remaining references to [Reference Hrushovski18] are mostly foundational lemmas. However, our Galois stratification procedure works over existentially closed difference fields unconditionally, without the use of [Reference Hrushovski18] (see 7.17).
One of the biggest challenges was the correct formulation of the result and even a suitable definition of a Galois cover, which already requires the full power of the theory of generalized difference schemes developed in [Reference Tomašić24], since the category of strict difference schemes has no reasonable Galois actions, covers or quotients. One clear advantage of the description of the definable sets in terms of (twisted) Galois stratifications is our ability to reduce considerations regarding points on definable sets to calculations of various character sums, as expounded in [Reference Tomašić24]. Since the style of our proof is reminiscent of many a direct image theorem from algebraic geometry, our results should appeal to algebraic geometers and number theorists and we expect more diophantine applications to follow.
Our approach to the proof of 1.1 (in fact of 7.12) is more geometric and conceptual than those of [Reference Fried and Jarden13], [Reference Fried and Sacerdote14], [Reference Fried, Haran and Jarden12] in the classical case. The proof from [Reference Nicaise22] in the algebraic case uses the theory of the étale fundamental group in a rather sophisticated way, which is not available in the difference scenario. However, by performing a “baby” Stein factorization at the start of our procedure, the only remnant of that theory is the short exact sequence for the étale fundamental group, in which case we can “manually” keep track of what happens at the level of finite Galois covers. From this point of view, even if we were to eliminate all the difference language, our line of proof would still yield an essentially new proof in the classical case. Here, on the other hand, we must treat several genuinely new difference phenomena which do not arise in the algebraic case. Key ingredients include Babbitt’s decomposition theorem 5.12 and our Chebotarev lemma [Reference Tomašić24, 4.28].
The foundation of the theory of generalized difference schemes has been laid in [Reference Tomašić24]. We give a gist of it in Section 2 and we develop the framework even further in Section 4.
In the course of the proof, we use local properties of difference schemes previously unknown in difference algebraic geometry, developed in Section 3. It must be emphasized that our theory is almost orthogonal to the various notions of smoothness that appear in Giabicani’s thesis [Reference Giabicani15] (see 3.31).
En route to the main theorem, we encounter another merit of working in the context of generalized difference schemes, a difference version of Chevalley’s theorem 7.7, which gives a sufficient condition for the image of a morphism of difference schemes of finite transformal type to contain a dense open set. Wibmer gives a similar result by generalizing difference algebra in a slightly different direction [Reference Wibmer26].
2 Generalized difference algebra and geometry
In this section, we give a summary of the theory of generalized difference schemes from [Reference Tomašić24]. The familiarity with this work is crucial and we often refer to numerous technical results from [Reference Tomašić24] we were not able to include here. However, the reader acquainted with [Reference Hrushovski18] may be able to follow the subsequent developments that refer to ordinary difference schemes.
2.1 Difference structures
Definition 2.1. Let us consider the category ![]() $\mathit{Diff}$ as follows. An object of
$\mathit{Diff}$ as follows. An object of ![]() $\mathit{Diff}$ is a set
$\mathit{Diff}$ is a set ![]() ${\rm\Sigma}$, equipped with a map
${\rm\Sigma}$, equipped with a map 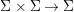 ${\rm\Sigma}\times {\rm\Sigma}\rightarrow {\rm\Sigma}$,
${\rm\Sigma}\times {\rm\Sigma}\rightarrow {\rm\Sigma}$, 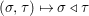 $({\it\sigma},{\it\tau})\mapsto {\it\sigma}\lhd {\it\tau}$ such that:
$({\it\sigma},{\it\tau})\mapsto {\it\sigma}\lhd {\it\tau}$ such that:
(1)
 ${\it\sigma}\lhd {\it\sigma}={\it\sigma}$;
${\it\sigma}\lhd {\it\sigma}={\it\sigma}$;(2)
 $\left({\it\sigma}\lhd {\it\tau}\right)\lhd {\it\upsilon}=\left({\it\sigma}\lhd {\it\upsilon}\right)\lhd \left({\it\tau}\lhd {\it\upsilon}\right)$ for all
$\left({\it\sigma}\lhd {\it\tau}\right)\lhd {\it\upsilon}=\left({\it\sigma}\lhd {\it\upsilon}\right)\lhd \left({\it\tau}\lhd {\it\upsilon}\right)$ for all  ${\it\sigma},{\it\tau},{\it\upsilon}\in {\rm\Sigma}$.
${\it\sigma},{\it\tau},{\it\upsilon}\in {\rm\Sigma}$.
A morphism 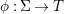 ${\it\phi}:{\rm\Sigma}\rightarrow T$ is a function such that for all
${\it\phi}:{\rm\Sigma}\rightarrow T$ is a function such that for all 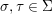 ${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
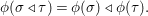 $$\begin{eqnarray}{\it\phi}({\it\sigma}\lhd {\it\tau})={\it\phi}({\it\sigma})\lhd {\it\phi}({\it\tau}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}({\it\sigma}\lhd {\it\tau})={\it\phi}({\it\sigma})\lhd {\it\phi}({\it\tau}).\end{eqnarray}$$ Inherently, for every ![]() ${\it\sigma}\in {\rm\Sigma}$, the map
${\it\sigma}\in {\rm\Sigma}$, the map 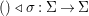 $()\lhd {\it\sigma}:{\rm\Sigma}\rightarrow {\rm\Sigma}$ is a
$()\lhd {\it\sigma}:{\rm\Sigma}\rightarrow {\rm\Sigma}$ is a ![]() $\mathit{Diff}$-morphism.
$\mathit{Diff}$-morphism.
Definition 2.2. The difference category of locally ringed spaces has objects of form ![]() $(X,{\rm\Sigma})$, where
$(X,{\rm\Sigma})$, where 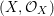 $(X,{\mathcal{O}}_{X})$ is a locally ringed space, and
$(X,{\mathcal{O}}_{X})$ is a locally ringed space, and ![]() ${\rm\Sigma}$ is a set of endomorphisms of
${\rm\Sigma}$ is a set of endomorphisms of ![]() $X$ such that there exists a function
$X$ such that there exists a function 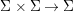 ${\rm\Sigma}\times {\rm\Sigma}\rightarrow {\rm\Sigma}$,
${\rm\Sigma}\times {\rm\Sigma}\rightarrow {\rm\Sigma}$, 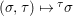 $({\it\sigma},{\it\tau})\mapsto \text{}^{{\it\tau}}{\it\sigma}$ with:
$({\it\sigma},{\it\tau})\mapsto \text{}^{{\it\tau}}{\it\sigma}$ with:
(1) for every
 ${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
${\it\sigma},{\it\tau}\in {\rm\Sigma}$,  $$\begin{eqnarray}\text{}^{{\it\tau}}{\it\sigma}\circ {\it\tau}={\it\tau}\circ {\it\sigma};\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{{\it\tau}}{\it\sigma}\circ {\it\tau}={\it\tau}\circ {\it\sigma};\end{eqnarray}$$(2)
 $\left({\rm\Sigma},({\it\sigma},{\it\tau})\mapsto \text{}^{{\it\tau}}{\it\sigma}\right)$ is an object of
$\left({\rm\Sigma},({\it\sigma},{\it\tau})\mapsto \text{}^{{\it\tau}}{\it\sigma}\right)$ is an object of  $\mathit{Diff}$.
$\mathit{Diff}$.
A morphism 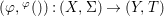 $({\it\varphi},\text{}^{{\it\varphi}}()):(X,{\rm\Sigma})\rightarrow (Y,T)$ consists of a
$({\it\varphi},\text{}^{{\it\varphi}}()):(X,{\rm\Sigma})\rightarrow (Y,T)$ consists of a ![]() $\mathit{Diff}$-morphism
$\mathit{Diff}$-morphism 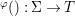 $\text{}^{{\it\varphi}}():{\rm\Sigma}\rightarrow T$ and a morphism of locally ringed spaces
$\text{}^{{\it\varphi}}():{\rm\Sigma}\rightarrow T$ and a morphism of locally ringed spaces 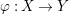 ${\it\varphi}:X\rightarrow Y$ such that for every
${\it\varphi}:X\rightarrow Y$ such that for every ![]() ${\it\sigma}\in {\rm\Sigma}$,
${\it\sigma}\in {\rm\Sigma}$,
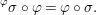 $$\begin{eqnarray}\text{}^{{\it\varphi}}{\it\sigma}\circ {\it\varphi}={\it\varphi}\circ {\it\sigma}.\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{{\it\varphi}}{\it\sigma}\circ {\it\varphi}={\it\varphi}\circ {\it\sigma}.\end{eqnarray}$$Definition 2.3. The category of difference rings has objects of form ![]() $(A,{\rm\Sigma})$, where
$(A,{\rm\Sigma})$, where ![]() $A$ is a commutative ring with identity and
$A$ is a commutative ring with identity and ![]() ${\rm\Sigma}$ is a set of endomorphisms
${\rm\Sigma}$ is a set of endomorphisms ![]() $A\rightarrow A$ such that there exists a function
$A\rightarrow A$ such that there exists a function 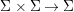 ${\rm\Sigma}\times {\rm\Sigma}\rightarrow {\rm\Sigma}$,
${\rm\Sigma}\times {\rm\Sigma}\rightarrow {\rm\Sigma}$, 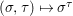 $({\it\sigma},{\it\tau})\mapsto {\it\sigma}^{{\it\tau}}$ with:
$({\it\sigma},{\it\tau})\mapsto {\it\sigma}^{{\it\tau}}$ with:
(1) for every
 ${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
${\it\sigma},{\it\tau}\in {\rm\Sigma}$,  $$\begin{eqnarray}{\it\tau}\circ {\it\sigma}^{{\it\tau}}={\it\sigma}\circ {\it\tau};\end{eqnarray}$$
$$\begin{eqnarray}{\it\tau}\circ {\it\sigma}^{{\it\tau}}={\it\sigma}\circ {\it\tau};\end{eqnarray}$$(2)
 $\left({\rm\Sigma},({\it\sigma},{\it\tau})\mapsto {\it\sigma}^{{\it\tau}}\right)$ is an object of
$\left({\rm\Sigma},({\it\sigma},{\it\tau})\mapsto {\it\sigma}^{{\it\tau}}\right)$ is an object of  $\mathit{Diff}$.
$\mathit{Diff}$.
A morphism 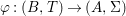 ${\it\varphi}:(B,T)\rightarrow (A,{\rm\Sigma})$ consists of a
${\it\varphi}:(B,T)\rightarrow (A,{\rm\Sigma})$ consists of a ![]() $\mathit{Diff}$-morphism
$\mathit{Diff}$-morphism 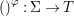 $()^{{\it\varphi}}:{\rm\Sigma}\rightarrow T$ and a ring homomorphism
$()^{{\it\varphi}}:{\rm\Sigma}\rightarrow T$ and a ring homomorphism 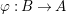 ${\it\varphi}:B\rightarrow A$ such that
${\it\varphi}:B\rightarrow A$ such that
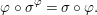 $$\begin{eqnarray}{\it\varphi}\circ {\it\sigma}^{{\it\varphi}}={\it\sigma}\circ {\it\varphi}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}\circ {\it\sigma}^{{\it\varphi}}={\it\sigma}\circ {\it\varphi}.\end{eqnarray}$$Definition 2.4. Each difference ring ![]() $(A,{\rm\Sigma})$ has a natural action of the free semigroup
$(A,{\rm\Sigma})$ has a natural action of the free semigroup ![]() $\langle {\rm\Sigma}\rangle$ generated by
$\langle {\rm\Sigma}\rangle$ generated by ![]() ${\rm\Sigma}$, as well as the ring
${\rm\Sigma}$, as well as the ring 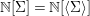 $\mathbb{N}[{\rm\Sigma}]=\mathbb{N}[\langle {\rm\Sigma}\rangle ]$ of positive integer combinations of elements of
$\mathbb{N}[{\rm\Sigma}]=\mathbb{N}[\langle {\rm\Sigma}\rangle ]$ of positive integer combinations of elements of ![]() $\langle {\rm\Sigma}\rangle$. The difference ring localization of
$\langle {\rm\Sigma}\rangle$. The difference ring localization of ![]() $A$ at
$A$ at ![]() $f\in A$ is
$f\in A$ is 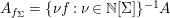 $A_{f_{{\rm\Sigma}}}=\{{\it\nu}f:{\it\nu}\in \mathbb{N}[{\rm\Sigma}]\}^{-1}A$.
$A_{f_{{\rm\Sigma}}}=\{{\it\nu}f:{\it\nu}\in \mathbb{N}[{\rm\Sigma}]\}^{-1}A$.
Definition 2.5. A difference ring ![]() $(A,{\rm\Sigma})$ is called
$(A,{\rm\Sigma})$ is called
(1) strong, or
 ${\rm\Sigma}$-reduced, if all endomorphisms in
${\rm\Sigma}$-reduced, if all endomorphisms in  ${\rm\Sigma}$ are injective;
${\rm\Sigma}$ are injective;(2) inversive, if every
 ${\it\sigma}\in {\rm\Sigma}$ is an automorphism of
${\it\sigma}\in {\rm\Sigma}$ is an automorphism of  $A$;
$A$;(3) almost-strict, if there exist a finite subgroup
 $G$ of
$G$ of  $\text{Aut}(A,{\rm\Sigma})$, an element
$\text{Aut}(A,{\rm\Sigma})$, an element  ${\it\sigma}\in {\rm\Sigma}$ and a group homomorphism
${\it\sigma}\in {\rm\Sigma}$ and a group homomorphism  $()^{{\it\sigma}}:G\rightarrow G$ such that
$()^{{\it\sigma}}:G\rightarrow G$ such that  ${\rm\Sigma}={\it\sigma}G$, and for all
${\rm\Sigma}={\it\sigma}G$, and for all  $g\in G$,
$g\in G$,  $g{\it\sigma}={\it\sigma}g^{{\it\sigma}}$. Consequently, the difference structure is given by
$g{\it\sigma}={\it\sigma}g^{{\it\sigma}}$. Consequently, the difference structure is given by  $$\begin{eqnarray}({\it\sigma}g)^{({\it\sigma}h)}={\it\sigma}(h^{-1}g)^{{\it\sigma}}\,h.\end{eqnarray}$$
$$\begin{eqnarray}({\it\sigma}g)^{({\it\sigma}h)}={\it\sigma}(h^{-1}g)^{{\it\sigma}}\,h.\end{eqnarray}$$
Every strong difference ring ![]() $(A,{\rm\Sigma})$ with
$(A,{\rm\Sigma})$ with ![]() ${\rm\Sigma}$ finite and every
${\rm\Sigma}$ finite and every 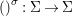 $()^{{\it\sigma}}:{\rm\Sigma}\rightarrow {\rm\Sigma}$ bijective has an inversive closure.
$()^{{\it\sigma}}:{\rm\Sigma}\rightarrow {\rm\Sigma}$ bijective has an inversive closure.
Definition 2.6. Let ![]() $I$ be an ideal in a difference ring
$I$ be an ideal in a difference ring ![]() $(A,{\rm\Sigma})$. We say that:
$(A,{\rm\Sigma})$. We say that:
(1)
 $I$ is a
$I$ is a  ${\rm\Sigma}$-ideal if
${\rm\Sigma}$-ideal if  ${\it\sigma}(I)\subseteq I$ for every
${\it\sigma}(I)\subseteq I$ for every  ${\it\sigma}\in {\rm\Sigma}$;
${\it\sigma}\in {\rm\Sigma}$;(2)
 $I$ is
$I$ is  ${\rm\Sigma}$-reflexive if
${\rm\Sigma}$-reflexive if  ${\it\sigma}^{-1}(I)=I$ for every
${\it\sigma}^{-1}(I)=I$ for every  ${\it\sigma}\in {\rm\Sigma}$;
${\it\sigma}\in {\rm\Sigma}$;(3)
 $I$ is
$I$ is  ${\rm\Sigma}$-well-mixed if
${\rm\Sigma}$-well-mixed if  $ab\in I$ implies
$ab\in I$ implies  $a\,{\it\sigma}(b)\in I$ for any
$a\,{\it\sigma}(b)\in I$ for any  ${\it\sigma}\in {\rm\Sigma}$;
${\it\sigma}\in {\rm\Sigma}$;(4)
 $A$ itself is well-mixed if the zero ideal is;
$A$ itself is well-mixed if the zero ideal is;(5)
 $I$ is
$I$ is  ${\rm\Sigma}$-perfect if for every
${\rm\Sigma}$-perfect if for every  ${\it\sigma}\in {\rm\Sigma}$,
${\it\sigma}\in {\rm\Sigma}$,  $a\,{\it\sigma}a\in I$ implies
$a\,{\it\sigma}a\in I$ implies  $a$ and
$a$ and  ${\it\sigma}a$ are both in
${\it\sigma}a$ are both in  $I$;
$I$;(6)
 $A$ is a transformal domain if
$A$ is a transformal domain if  $(A,{\rm\Sigma})$ is strong and
$(A,{\rm\Sigma})$ is strong and  $A$ is a domain.
$A$ is a domain.
2.2 Difference spectra
Definition 2.7. Let ![]() $(R,{\rm\Sigma})$ be a difference ring. We consider each of the following subsets of
$(R,{\rm\Sigma})$ be a difference ring. We consider each of the following subsets of 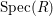 $\text{Spec}(R)$ as locally ringed spaces with the Zariski topology and the structure sheaves induced from
$\text{Spec}(R)$ as locally ringed spaces with the Zariski topology and the structure sheaves induced from 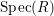 $\text{Spec}(R)$:
$\text{Spec}(R)$:
(1)
 $\text{Spec}^{{\it\sigma}}(R)=\{\mathfrak{p}\in \text{Spec}(R):{\it\sigma}^{-1}(\mathfrak{p})=\mathfrak{p}\}$, for any
$\text{Spec}^{{\it\sigma}}(R)=\{\mathfrak{p}\in \text{Spec}(R):{\it\sigma}^{-1}(\mathfrak{p})=\mathfrak{p}\}$, for any  ${\it\sigma}\in {\rm\Sigma}$;
${\it\sigma}\in {\rm\Sigma}$;(2)
 $\text{Spec}^{{\rm\Sigma}}(R)=\cup _{{\it\sigma}\in {\rm\Sigma}}\text{Spec}^{{\it\sigma}}(R)$.
$\text{Spec}^{{\rm\Sigma}}(R)=\cup _{{\it\sigma}\in {\rm\Sigma}}\text{Spec}^{{\it\sigma}}(R)$.
In discussions of induced topology, we use the notation ![]() $V^{{\it\sigma}}(I)$,
$V^{{\it\sigma}}(I)$, ![]() $D^{{\it\sigma}}(I)$,
$D^{{\it\sigma}}(I)$, ![]() $V^{{\rm\Sigma}}(I)$,
$V^{{\rm\Sigma}}(I)$, ![]() $D^{{\rm\Sigma}}(I)$, for the traces of
$D^{{\rm\Sigma}}(I)$, for the traces of ![]() $V(I)$ and
$V(I)$ and ![]() $D(I)$ on
$D(I)$ on 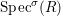 $\text{Spec}^{{\it\sigma}}(R)$,
$\text{Spec}^{{\it\sigma}}(R)$, 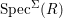 $\text{Spec}^{{\rm\Sigma}}(R)$, respectively.
$\text{Spec}^{{\rm\Sigma}}(R)$, respectively.
Writing 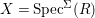 $X=\text{Spec}^{{\rm\Sigma}}(R)$, bearing in mind that for
$X=\text{Spec}^{{\rm\Sigma}}(R)$, bearing in mind that for 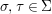 ${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
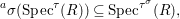 $$\begin{eqnarray}\text{}^{a}{\it\sigma}(\text{Spec}^{{\it\tau}}(R))\subseteq \text{Spec}^{{\it\tau}^{{\it\sigma}}}(R),\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{a}{\it\sigma}(\text{Spec}^{{\it\tau}}(R))\subseteq \text{Spec}^{{\it\tau}^{{\it\sigma}}}(R),\end{eqnarray}$$ each ![]() ${\it\sigma}\in {\rm\Sigma}$ induces the morphism of locally ringed spaces
${\it\sigma}\in {\rm\Sigma}$ induces the morphism of locally ringed spaces ![]() $(\text{}^{a}{\it\sigma},\tilde{{\it\sigma}})$
$(\text{}^{a}{\it\sigma},\tilde{{\it\sigma}})$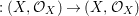 $:(X,{\mathcal{O}}_{X})\rightarrow (X,{\mathcal{O}}_{X})$. Consequently, the locally ringed space
$:(X,{\mathcal{O}}_{X})\rightarrow (X,{\mathcal{O}}_{X})$. Consequently, the locally ringed space 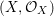 $(X,{\mathcal{O}}_{X})$ is equipped with a set of endomorphisms of locally ringed spaces
$(X,{\mathcal{O}}_{X})$ is equipped with a set of endomorphisms of locally ringed spaces
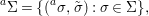 $$\begin{eqnarray}\text{}^{a}{\rm\Sigma}=\{(\text{}^{a}{\it\sigma},\tilde{{\it\sigma}}):{\it\sigma}\in {\rm\Sigma}\},\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{a}{\rm\Sigma}=\{(\text{}^{a}{\it\sigma},\tilde{{\it\sigma}}):{\it\sigma}\in {\rm\Sigma}\},\end{eqnarray}$$ which is closed under “conjugation” through the relation 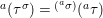 $\text{}^{a}({\it\tau}^{{\it\sigma}})=\text{}^{(\text{}^{a}{\it\sigma})}(\text{}^{a}{\it\tau})$, making
$\text{}^{a}({\it\tau}^{{\it\sigma}})=\text{}^{(\text{}^{a}{\it\sigma})}(\text{}^{a}{\it\tau})$, making 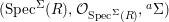 $(\text{Spec}^{{\rm\Sigma}}(R),{\mathcal{O}}_{\text{Spec}^{{\rm\Sigma}}(R)},\text{}^{a}{\rm\Sigma})$ into a difference locally ringed space.
$(\text{Spec}^{{\rm\Sigma}}(R),{\mathcal{O}}_{\text{Spec}^{{\rm\Sigma}}(R)},\text{}^{a}{\rm\Sigma})$ into a difference locally ringed space.
Similarly, a morphism 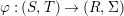 ${\it\varphi}:(S,T)\rightarrow (R,{\rm\Sigma})$ of difference rings satisfies
${\it\varphi}:(S,T)\rightarrow (R,{\rm\Sigma})$ of difference rings satisfies
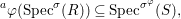 $$\begin{eqnarray}\text{}^{a}{\it\varphi}(\text{Spec}^{{\it\sigma}}(R))\subseteq \text{Spec}^{{\it\sigma}^{{\it\varphi}}}(S),\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{a}{\it\varphi}(\text{Spec}^{{\it\sigma}}(R))\subseteq \text{Spec}^{{\it\sigma}^{{\it\varphi}}}(S),\end{eqnarray}$$and it gives rise to a morphism in the difference category of locally ringed spaces
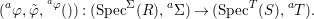 $$\begin{eqnarray}(\text{}^{a}{\it\varphi},\tilde{{\it\varphi}},\text{}^{\text{}^{a}{\it\varphi}}()):(\text{Spec}^{{\rm\Sigma}}(R),\text{}^{a}{\rm\Sigma})\rightarrow (\text{Spec}^{T}(S),\text{}^{a}T).\end{eqnarray}$$
$$\begin{eqnarray}(\text{}^{a}{\it\varphi},\tilde{{\it\varphi}},\text{}^{\text{}^{a}{\it\varphi}}()):(\text{Spec}^{{\rm\Sigma}}(R),\text{}^{a}{\rm\Sigma})\rightarrow (\text{Spec}^{T}(S),\text{}^{a}T).\end{eqnarray}$$ This makes ![]() $\text{Spec}$ into a contravariant functor from the category of difference rings to the difference category of locally ringed spaces which respects the difference structure.
$\text{Spec}$ into a contravariant functor from the category of difference rings to the difference category of locally ringed spaces which respects the difference structure.
Fact 2.8. Let ![]() $(A,{\rm\Sigma})$ be a well-mixed difference ring with finite
$(A,{\rm\Sigma})$ be a well-mixed difference ring with finite ![]() ${\rm\Sigma}$ so that
${\rm\Sigma}$ so that 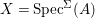 $X=\text{Spec}^{{\rm\Sigma}}(A)$ is quasicompact.
$X=\text{Spec}^{{\rm\Sigma}}(A)$ is quasicompact.
(1) The canonical morphism
 $i:A\rightarrow \bar{A}=H^{0}(X)={\mathcal{O}}_{X}(X)$ is injective and induces an isomorphism of difference schemes
$i:A\rightarrow \bar{A}=H^{0}(X)={\mathcal{O}}_{X}(X)$ is injective and induces an isomorphism of difference schemes  $$\begin{eqnarray}(\text{}^{a}i,\tilde{\imath }):\text{Spec}^{{\rm\Sigma}}(\bar{A})\stackrel{{\sim}}{\rightarrow }\text{Spec}^{{\rm\Sigma}}(A).\end{eqnarray}$$
$$\begin{eqnarray}(\text{}^{a}i,\tilde{\imath }):\text{Spec}^{{\rm\Sigma}}(\bar{A})\stackrel{{\sim}}{\rightarrow }\text{Spec}^{{\rm\Sigma}}(A).\end{eqnarray}$$(2) Consequently, the functor
 $H^{0}$ is left adjoint to
$H^{0}$ is left adjoint to  $\text{Spec}$.
$\text{Spec}$.
2.3 Difference schemes
(1) An affine difference scheme is an object
 $(X,{\mathcal{O}}_{X},{\rm\Sigma})$ of the difference category of locally ringed spaces, which is isomorphic to
$(X,{\mathcal{O}}_{X},{\rm\Sigma})$ of the difference category of locally ringed spaces, which is isomorphic to  $\text{Spec}^{{\rm\Sigma}}(A)$ for some difference ring
$\text{Spec}^{{\rm\Sigma}}(A)$ for some difference ring  $(A,{\rm\Sigma})$.
$(A,{\rm\Sigma})$.(2) A difference scheme is an object
 $(X,{\mathcal{O}}_{X},{\rm\Sigma})$ of the difference category of locally ringed spaces, which is locally an affine difference scheme.
$(X,{\mathcal{O}}_{X},{\rm\Sigma})$ of the difference category of locally ringed spaces, which is locally an affine difference scheme.(3) A morphism of difference schemes
 $(X,{\mathcal{O}}_{X},{\rm\Sigma})\rightarrow (Y,{\mathcal{O}}_{Y},T)$ is just a morphism in the difference category of locally ringed spaces.
$(X,{\mathcal{O}}_{X},{\rm\Sigma})\rightarrow (Y,{\mathcal{O}}_{Y},T)$ is just a morphism in the difference category of locally ringed spaces.
Definition 2.10. Let ![]() $(X,{\rm\Sigma})$ be a difference scheme and
$(X,{\rm\Sigma})$ be a difference scheme and ![]() $x\in X$ a point. Let
$x\in X$ a point. Let
 $$\begin{eqnarray}{\rm\Sigma}_{x}=\{{\it\sigma}\in {\rm\Sigma}:{\it\sigma}(x)=x\},\quad {\rm\Sigma}_{x}^{\sharp }=\{{\it\sigma}_{x}^{\sharp }:{\it\sigma}\in {\rm\Sigma}_{x}\},\quad \text{and}\quad {\rm\Sigma}^{x}=\{{\it\sigma}^{x}:{\it\sigma}\in {\rm\Sigma}_{x}\},\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Sigma}_{x}=\{{\it\sigma}\in {\rm\Sigma}:{\it\sigma}(x)=x\},\quad {\rm\Sigma}_{x}^{\sharp }=\{{\it\sigma}_{x}^{\sharp }:{\it\sigma}\in {\rm\Sigma}_{x}\},\quad \text{and}\quad {\rm\Sigma}^{x}=\{{\it\sigma}^{x}:{\it\sigma}\in {\rm\Sigma}_{x}\},\end{eqnarray}$$ where 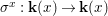 ${\it\sigma}^{x}:\mathbf{k}(x)\rightarrow \mathbf{k}(x)$ is induced by the local morphism
${\it\sigma}^{x}:\mathbf{k}(x)\rightarrow \mathbf{k}(x)$ is induced by the local morphism 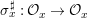 ${\it\sigma}_{x}^{\sharp }:{\mathcal{O}}_{x}\rightarrow {\mathcal{O}}_{x}$ associated with each
${\it\sigma}_{x}^{\sharp }:{\mathcal{O}}_{x}\rightarrow {\mathcal{O}}_{x}$ associated with each ![]() ${\it\sigma}\in {\rm\Sigma}_{x}$. This yields a difference local ring
${\it\sigma}\in {\rm\Sigma}_{x}$. This yields a difference local ring 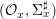 $({\mathcal{O}}_{x},{\rm\Sigma}_{x}^{\sharp })$ with difference residue field
$({\mathcal{O}}_{x},{\rm\Sigma}_{x}^{\sharp })$ with difference residue field 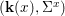 $(\mathbf{k}(x),{\rm\Sigma}^{x})$.
$(\mathbf{k}(x),{\rm\Sigma}^{x})$.
Definition 2.11. A difference scheme 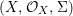 $(X,{\mathcal{O}}_{X},{\rm\Sigma})$ is said to be:
$(X,{\mathcal{O}}_{X},{\rm\Sigma})$ is said to be:
(1) reduced, if the nilradical of each
 ${\mathcal{O}}_{x}$ is trivial;
${\mathcal{O}}_{x}$ is trivial;(2) perfectly reduced, if the perfect closure of
 $0$ in each
$0$ in each  ${\mathcal{O}}_{x}$ is trivial;
${\mathcal{O}}_{x}$ is trivial;(3) irreducible (resp. connected) if its underlying topological space is;
(4) integral (resp. transformally integral) if it is irreducible and reduced (resp. perfectly reduced);
(5) well-mixed, if each
 ${\mathcal{O}}_{x}$ is well-mixed.
${\mathcal{O}}_{x}$ is well-mixed.
We often work in a relative setting, over a chosen base scheme ![]() $(S,{\rm\Sigma}_{0})$ or a base difference ring
$(S,{\rm\Sigma}_{0})$ or a base difference ring ![]() $(R,{\rm\Sigma}_{0})$. An
$(R,{\rm\Sigma}_{0})$. An ![]() $S$-scheme is a difference scheme morphism
$S$-scheme is a difference scheme morphism 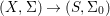 $(X,{\rm\Sigma})\rightarrow (S,{\rm\Sigma}_{0})$, and morphisms between
$(X,{\rm\Sigma})\rightarrow (S,{\rm\Sigma}_{0})$, and morphisms between ![]() $S$-difference schemes are required to preserve the structural morphisms to
$S$-difference schemes are required to preserve the structural morphisms to ![]() $S$. Similarly, an
$S$. Similarly, an ![]() $(R,{\rm\Sigma}_{0})$-difference scheme is locally of the form
$(R,{\rm\Sigma}_{0})$-difference scheme is locally of the form 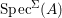 $\text{Spec}^{{\rm\Sigma}}(A)$, for a difference
$\text{Spec}^{{\rm\Sigma}}(A)$, for a difference ![]() $(R,{\rm\Sigma}_{0})$-algebra
$(R,{\rm\Sigma}_{0})$-algebra ![]() $(A,{\rm\Sigma})$, and morphisms are required to locally preserve the
$(A,{\rm\Sigma})$, and morphisms are required to locally preserve the ![]() $(R,{\rm\Sigma}_{0})$-algebra structure.
$(R,{\rm\Sigma}_{0})$-algebra structure.
Definition 2.12. Let ![]() $(X,{\rm\Sigma})$ be a difference scheme and
$(X,{\rm\Sigma})$ be a difference scheme and ![]() $(K,{\it\varphi})$ a difference field. The set of
$(K,{\it\varphi})$ a difference field. The set of ![]() $(K,{\it\varphi})$-rational points of
$(K,{\it\varphi})$-rational points of ![]() $(X,{\rm\Sigma})$ is the set
$(X,{\rm\Sigma})$ is the set
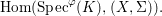 $$\begin{eqnarray}\text{Hom}(\text{Spec}^{{\it\varphi}}(K),(X,{\rm\Sigma})).\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}(\text{Spec}^{{\it\varphi}}(K),(X,{\rm\Sigma})).\end{eqnarray}$$In a relative setting, the points are required to factor through the base. A geometric point of a difference scheme is a point with values in an algebraically closed difference field.
In order for a fiber product 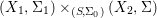 $(X_{1},{\rm\Sigma}_{1})\times _{(S,{\rm\Sigma}_{0})}(X_{2},{\rm\Sigma})$ to exist, the factors have to be compatible in a suitable sense. However, this technical difficulty is largely overcome by the framework of generalized difference schemes and we can ensure that all the products we form in subsequent sections are compatible.
$(X_{1},{\rm\Sigma}_{1})\times _{(S,{\rm\Sigma}_{0})}(X_{2},{\rm\Sigma})$ to exist, the factors have to be compatible in a suitable sense. However, this technical difficulty is largely overcome by the framework of generalized difference schemes and we can ensure that all the products we form in subsequent sections are compatible.
Definition 2.13. Let 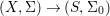 $(X,{\rm\Sigma})\rightarrow (S,{\rm\Sigma}_{0})$ be a morphism of difference schemes, considered as a family parametrized by
$(X,{\rm\Sigma})\rightarrow (S,{\rm\Sigma}_{0})$ be a morphism of difference schemes, considered as a family parametrized by ![]() $S$. Let
$S$. Let ![]() $(K,{\it\varphi})$ be a difference field and let
$(K,{\it\varphi})$ be a difference field and let 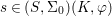 $s\in (S,{\rm\Sigma}_{0})(K,{\it\varphi})$. The fiber
$s\in (S,{\rm\Sigma}_{0})(K,{\it\varphi})$. The fiber ![]() $X_{s}$ is the
$X_{s}$ is the ![]() $(K,{\it\varphi})$-difference scheme obtained by base change via the morphism
$(K,{\it\varphi})$-difference scheme obtained by base change via the morphism 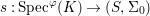 $s:\text{Spec}^{{\it\varphi}}(K)\rightarrow (S,{\rm\Sigma}_{0})$,
$s:\text{Spec}^{{\it\varphi}}(K)\rightarrow (S,{\rm\Sigma}_{0})$,
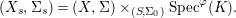 $$\begin{eqnarray}(X_{s},{\rm\Sigma}_{s})=(X,{\rm\Sigma})\times _{(S,{\rm\Sigma}_{0})}\text{Spec}^{{\it\varphi}}(K).\end{eqnarray}$$
$$\begin{eqnarray}(X_{s},{\rm\Sigma}_{s})=(X,{\rm\Sigma})\times _{(S,{\rm\Sigma}_{0})}\text{Spec}^{{\it\varphi}}(K).\end{eqnarray}$$ Let ![]() $P$ be a property of difference schemes. If
$P$ be a property of difference schemes. If 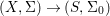 $(X,{\rm\Sigma})\rightarrow (S,{\rm\Sigma}_{0})$ is a difference scheme over a given base, we shall say that
$(X,{\rm\Sigma})\rightarrow (S,{\rm\Sigma}_{0})$ is a difference scheme over a given base, we shall say that ![]() $X$ is geometrically
$X$ is geometrically ![]() $P$, if every base change of
$P$, if every base change of ![]() $X$ has the property
$X$ has the property ![]() $P$.
$P$.
Definition 2.14. Let ![]() $(R,{\rm\Sigma}_{0})$ be a difference ring.
$(R,{\rm\Sigma}_{0})$ be a difference ring.
(1) An
 $(R,{\rm\Sigma}_{0})$-algebra
$(R,{\rm\Sigma}_{0})$-algebra  $(A,{\rm\Sigma})$ is of finite
$(A,{\rm\Sigma})$ is of finite  ${\rm\Sigma}$-type if there exist elements
${\rm\Sigma}$-type if there exist elements  $a_{1},\ldots ,a_{n}$ in
$a_{1},\ldots ,a_{n}$ in  $A$ such that
$A$ such that  $A=R[a_{1},\ldots ,a_{n}]_{{\rm\Sigma}}=R[{\it\nu}a_{1},\ldots ,{\it\nu}a_{n}:{\it\nu}\in \langle {\rm\Sigma}\rangle ]$.
$A=R[a_{1},\ldots ,a_{n}]_{{\rm\Sigma}}=R[{\it\nu}a_{1},\ldots ,{\it\nu}a_{n}:{\it\nu}\in \langle {\rm\Sigma}\rangle ]$.(2) An
 $(R,{\rm\Sigma}_{0})$-difference scheme
$(R,{\rm\Sigma}_{0})$-difference scheme  $(X,{\rm\Sigma})$ is of finite
$(X,{\rm\Sigma})$ is of finite  ${\rm\Sigma}$-type, or of finite transformal type if it is a finite union of affine difference schemes of the form
${\rm\Sigma}$-type, or of finite transformal type if it is a finite union of affine difference schemes of the form  $\text{Spec}^{{\rm\Sigma}}(A)$, where
$\text{Spec}^{{\rm\Sigma}}(A)$, where  $(A,{\rm\Sigma})$ is of finite
$(A,{\rm\Sigma})$ is of finite  ${\rm\Sigma}$-type over
${\rm\Sigma}$-type over  $(R,{\rm\Sigma}_{0})$.
$(R,{\rm\Sigma}_{0})$.(3) A morphism
 $f:(X,{\rm\Sigma})\rightarrow (Y,{\rm\Sigma}_{0})$ is of finite
$f:(X,{\rm\Sigma})\rightarrow (Y,{\rm\Sigma}_{0})$ is of finite  ${\rm\Sigma}$-type if
${\rm\Sigma}$-type if  $Y$ is a finite union of open affine subsets
$Y$ is a finite union of open affine subsets  $V_{i}=\text{Spec}^{{\rm\Sigma}_{0}}(R_{i})$ such that for each
$V_{i}=\text{Spec}^{{\rm\Sigma}_{0}}(R_{i})$ such that for each  $i$,
$i$,  $f^{-1}(V_{i})$ is of finite
$f^{-1}(V_{i})$ is of finite  ${\rm\Sigma}$-type over
${\rm\Sigma}$-type over  $(R_{i},{\rm\Sigma}_{0})$.
$(R_{i},{\rm\Sigma}_{0})$.(4) A morphism
 $f:(X,{\rm\Sigma})\rightarrow (Y,{\rm\Sigma}_{0})$ is integral (resp. finite) if
$f:(X,{\rm\Sigma})\rightarrow (Y,{\rm\Sigma}_{0})$ is integral (resp. finite) if  $Y$ is a finite union of open affine subsets
$Y$ is a finite union of open affine subsets  $V_{i}=\text{Spec}^{{\rm\Sigma}_{0}}(R_{i})$ such that for each
$V_{i}=\text{Spec}^{{\rm\Sigma}_{0}}(R_{i})$ such that for each  $i$,
$i$,  $f^{-1}(V_{i})$ is
$f^{-1}(V_{i})$ is  $\text{Spec}^{{\rm\Sigma}}(A_{i})$, where
$\text{Spec}^{{\rm\Sigma}}(A_{i})$, where  $A_{i}$ is integral (resp. finite) over
$A_{i}$ is integral (resp. finite) over  $R_{i}$.
$R_{i}$.
Definition 2.15. A difference ring ![]() $(R,{\rm\Sigma})$ is Ritt if it has the ascending chain condition on
$(R,{\rm\Sigma})$ is Ritt if it has the ascending chain condition on ![]() ${\rm\Sigma}$-perfect ideals.
${\rm\Sigma}$-perfect ideals.
It is classically known [Reference Cohn7] that every difference ring of finite ![]() ${\it\sigma}$-type over a Ritt difference ring is Ritt, or, equivalently, that difference schemes of finite
${\it\sigma}$-type over a Ritt difference ring is Ritt, or, equivalently, that difference schemes of finite ![]() ${\it\sigma}$-type over a Ritt difference ring are topologically Noetherian. Moreover, a perfectly reduced difference scheme decomposes into transformally integral components.
${\it\sigma}$-type over a Ritt difference ring are topologically Noetherian. Moreover, a perfectly reduced difference scheme decomposes into transformally integral components.
In the generalized context, we have the following.
Fact 2.16. Let ![]() $(S,{\rm\Sigma})$ be an almost-strict algebra of finite
$(S,{\rm\Sigma})$ be an almost-strict algebra of finite ![]() ${\rm\Sigma}$-type over a Ritt ring
${\rm\Sigma}$-type over a Ritt ring ![]() $(R,{\it\sigma}_{0})$, and
$(R,{\it\sigma}_{0})$, and ![]() ${\rm\Sigma}$ finite. Then
${\rm\Sigma}$ finite. Then 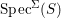 $\text{Spec}^{{\rm\Sigma}}(S)$ is topologically Noetherian and
$\text{Spec}^{{\rm\Sigma}}(S)$ is topologically Noetherian and ![]() $S$ has an ascending chain condition on ideals which are perfect with respect to any
$S$ has an ascending chain condition on ideals which are perfect with respect to any ![]() ${\it\sigma}\in {\rm\Sigma}$.
${\it\sigma}\in {\rm\Sigma}$.
2.4 Galois covers
Definition 2.17. A difference group ![]() $(G,{\rm\Sigma})$ is a group
$(G,{\rm\Sigma})$ is a group ![]() $G$, together with a
$G$, together with a ![]() $\mathit{Diff}$-structure
$\mathit{Diff}$-structure ![]() ${\rm\Sigma}$ of group endomorphisms satisfying the properties from 2.2 (more precisely, it is an object of the difference category over the category of groups in the sense of [Reference Tomašić24, 2.2]).
${\rm\Sigma}$ of group endomorphisms satisfying the properties from 2.2 (more precisely, it is an object of the difference category over the category of groups in the sense of [Reference Tomašić24, 2.2]).
We say that a group ![]() $(G,\text{}_{\llcorner }\!{\rm\Sigma})$acts (on the left) by automorphisms on a ring
$(G,\text{}_{\llcorner }\!{\rm\Sigma})$acts (on the left) by automorphisms on a ring ![]() $(A,{\rm\Sigma})$, if every
$(A,{\rm\Sigma})$, if every ![]() ${\it\sigma}\in {\rm\Sigma}$ corresponds to an endomorphism
${\it\sigma}\in {\rm\Sigma}$ corresponds to an endomorphism 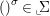 $()^{{\it\sigma}}\in \text{}_{\llcorner }\!{\rm\Sigma}$ of
$()^{{\it\sigma}}\in \text{}_{\llcorner }\!{\rm\Sigma}$ of ![]() $G$ so that, for every
$G$ so that, for every ![]() $g\in G$ and
$g\in G$ and 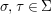 ${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
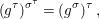 $$\begin{eqnarray}\left(g^{{\it\tau}}\right)^{{\it\sigma}^{{\it\tau}}}=\left(g^{{\it\sigma}}\right)^{{\it\tau}},\end{eqnarray}$$
$$\begin{eqnarray}\left(g^{{\it\tau}}\right)^{{\it\sigma}^{{\it\tau}}}=\left(g^{{\it\sigma}}\right)^{{\it\tau}},\end{eqnarray}$$ and, in  $\text{End}(A)$, we have the relation
$\text{End}(A)$, we have the relation
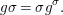 $$\begin{eqnarray}g{\it\sigma}={\it\sigma}g^{{\it\sigma}}.\end{eqnarray}$$
$$\begin{eqnarray}g{\it\sigma}={\it\sigma}g^{{\it\sigma}}.\end{eqnarray}$$ We invite the reader to formulate dual axioms for an action of a difference group ![]() $(G,{\rm\Sigma}\!_{\lrcorner })$ on a locally ringed space
$(G,{\rm\Sigma}\!_{\lrcorner })$ on a locally ringed space ![]() $(X,{\rm\Sigma})$, where each
$(X,{\rm\Sigma})$, where each ![]() ${\it\sigma}\in {\rm\Sigma}$ corresponds to an endomorphism
${\it\sigma}\in {\rm\Sigma}$ corresponds to an endomorphism ![]() $\text{}^{{\it\sigma}}()\in {\rm\Sigma}\!_{\lrcorner }$ of
$\text{}^{{\it\sigma}}()\in {\rm\Sigma}\!_{\lrcorner }$ of ![]() $G$.
$G$.
Remark 2.18. If ![]() $(G,\text{}_{\llcorner }\!{\rm\Sigma})$ acts on
$(G,\text{}_{\llcorner }\!{\rm\Sigma})$ acts on ![]() $(A,{\rm\Sigma})$, then
$(A,{\rm\Sigma})$, then 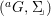 $(\text{}^{a}G,{\rm\Sigma}\!_{\lrcorner })$ acts on
$(\text{}^{a}G,{\rm\Sigma}\!_{\lrcorner })$ acts on 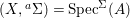 $(X,\text{}^{a}{\rm\Sigma})=\text{Spec}^{{\rm\Sigma}}(A)$ for
$(X,\text{}^{a}{\rm\Sigma})=\text{Spec}^{{\rm\Sigma}}(A)$ for 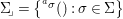 ${\rm\Sigma}\!_{\lrcorner }=\left\{\text{}^{\text{}^{a}{\it\sigma}}():{\it\sigma}\in {\rm\Sigma}\right\}$.
${\rm\Sigma}\!_{\lrcorner }=\left\{\text{}^{\text{}^{a}{\it\sigma}}():{\it\sigma}\in {\rm\Sigma}\right\}$.
Notation 2.19. Identifying the two difference groups from the remark, by a slight abuse of notation, we henceforth write ![]() $\tilde{{\rm\Sigma}}$ for either of
$\tilde{{\rm\Sigma}}$ for either of ![]() $\text{}_{\llcorner }\!{\rm\Sigma},{\rm\Sigma}\!_{\lrcorner }$, so that we can think of a difference group
$\text{}_{\llcorner }\!{\rm\Sigma},{\rm\Sigma}\!_{\lrcorner }$, so that we can think of a difference group ![]() $(G,\tilde{{\rm\Sigma}})$ acting both on algebraic and geometric objects.
$(G,\tilde{{\rm\Sigma}})$ acting both on algebraic and geometric objects.
Lemma 2.20. Let ![]() $(A,{\it\sigma})$ be a transformal domain. Suppose that a finite group
$(A,{\it\sigma})$ be a transformal domain. Suppose that a finite group ![]() $G$ acts on
$G$ acts on ![]() $A$ so that, writing
$A$ so that, writing 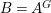 $B=A^{G}$, we have
$B=A^{G}$, we have 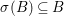 ${\it\sigma}(B)\subseteq B$. Let
${\it\sigma}(B)\subseteq B$. Let 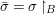 $\bar{{\it\sigma}}={\it\sigma}\restriction_{B}$. Then there exists a homomorphism
$\bar{{\it\sigma}}={\it\sigma}\restriction_{B}$. Then there exists a homomorphism 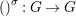 $()^{{\it\sigma}}:G\rightarrow G$ satisfying
$()^{{\it\sigma}}:G\rightarrow G$ satisfying 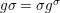 $g{\it\sigma}={\it\sigma}g^{{\it\sigma}}$ for
$g{\it\sigma}={\it\sigma}g^{{\it\sigma}}$ for ![]() $g\in G$, making
$g\in G$, making ![]() $(A,{\rm\Sigma})$, for
$(A,{\rm\Sigma})$, for 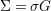 ${\rm\Sigma}={\it\sigma}G$, into an almost-strict extension of
${\rm\Sigma}={\it\sigma}G$, into an almost-strict extension of ![]() $(B,\bar{{\it\sigma}})$ with automorphism group
$(B,\bar{{\it\sigma}})$ with automorphism group ![]() $(G,\tilde{{\rm\Sigma}})$, where
$(G,\tilde{{\rm\Sigma}})$, where 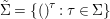 $\tilde{{\rm\Sigma}}=\{()^{{\it\tau}}:{\it\tau}\in {\rm\Sigma}\}$.
$\tilde{{\rm\Sigma}}=\{()^{{\it\tau}}:{\it\tau}\in {\rm\Sigma}\}$.
Proof. For a ![]() $g\in G$, consider
$g\in G$, consider ![]() $f_{1}=j{\it\sigma}$,
$f_{1}=j{\it\sigma}$, 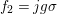 $f_{2}=jg{\it\sigma}$, where
$f_{2}=jg{\it\sigma}$, where ![]() $j$ injects
$j$ injects ![]() $A$ into its fraction field. Since
$A$ into its fraction field. Since 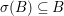 ${\it\sigma}(B)\subseteq B$, we verify that
${\it\sigma}(B)\subseteq B$, we verify that 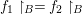 $f_{1}\restriction_{B}=f_{2}\restriction_{B}$, so [Reference Bourbaki5, V, Section 2.3, Corollaire 1] yields a
$f_{1}\restriction_{B}=f_{2}\restriction_{B}$, so [Reference Bourbaki5, V, Section 2.3, Corollaire 1] yields a ![]() $h\in G$ such that
$h\in G$ such that 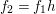 $f_{2}=f_{1}h$. By injectivity of
$f_{2}=f_{1}h$. By injectivity of ![]() $j$, we get
$j$, we get 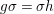 $g{\it\sigma}={\it\sigma}h$. Since
$g{\it\sigma}={\it\sigma}h$. Since ![]() ${\it\sigma}$ is injective,
${\it\sigma}$ is injective, ![]() $h$ is unique and we can write
$h$ is unique and we can write ![]() $h=g^{{\it\sigma}}$. ◻
$h=g^{{\it\sigma}}$. ◻
Corollary 2.21. Let 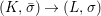 $(K,\bar{{\it\sigma}})\rightarrow (L,{\it\sigma})$ be a difference field extension where
$(K,\bar{{\it\sigma}})\rightarrow (L,{\it\sigma})$ be a difference field extension where ![]() $L/K$ is Galois with group
$L/K$ is Galois with group ![]() $G$. Let
$G$. Let ![]() ${\rm\Sigma}$ be the set of all lifts of
${\rm\Sigma}$ be the set of all lifts of ![]() $\bar{{\it\sigma}}$ to
$\bar{{\it\sigma}}$ to ![]() $L$. Then
$L$. Then 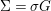 ${\rm\Sigma}={\it\sigma}G$ and we have endomorphisms
${\rm\Sigma}={\it\sigma}G$ and we have endomorphisms 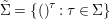 $\tilde{{\rm\Sigma}}=\{()^{{\it\tau}}:{\it\tau}\in {\rm\Sigma}\}$ of
$\tilde{{\rm\Sigma}}=\{()^{{\it\tau}}:{\it\tau}\in {\rm\Sigma}\}$ of ![]() $G$ such that
$G$ such that ![]() $(G,\tilde{{\rm\Sigma}})$ is the group of automorphisms of
$(G,\tilde{{\rm\Sigma}})$ is the group of automorphisms of ![]() $(L,{\rm\Sigma})$ over
$(L,{\rm\Sigma})$ over ![]() $(K,\bar{{\it\sigma}})$.
$(K,\bar{{\it\sigma}})$.
Proposition 2.22. Suppose a finite group ![]() $(G,\tilde{{\rm\Sigma}})$ acts on the left on a difference ring
$(G,\tilde{{\rm\Sigma}})$ acts on the left on a difference ring ![]() $(A,{\rm\Sigma})$, and
$(A,{\rm\Sigma})$, and 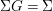 ${\rm\Sigma}G={\rm\Sigma}$. Consequently,
${\rm\Sigma}G={\rm\Sigma}$. Consequently, ![]() $G$ acts on the right on
$G$ acts on the right on 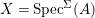 $X=\text{Spec}^{{\rm\Sigma}}(A)$ via
$X=\text{Spec}^{{\rm\Sigma}}(A)$ via 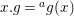 $x.g=\text{}^{a}g(x)$. Let
$x.g=\text{}^{a}g(x)$. Let 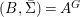 $(B,\bar{{\rm\Sigma}})=A^{G}$ be the subring of invariants of
$(B,\bar{{\rm\Sigma}})=A^{G}$ be the subring of invariants of ![]() $A$,
$A$, 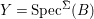 $Y=\text{Spec}^{\bar{{\rm\Sigma}}}(B)$ and let
$Y=\text{Spec}^{\bar{{\rm\Sigma}}}(B)$ and let 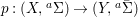 $p:(X,\text{}^{a}{\rm\Sigma})\rightarrow (Y,\text{}^{a}\bar{{\rm\Sigma}})$ be the canonical (
$p:(X,\text{}^{a}{\rm\Sigma})\rightarrow (Y,\text{}^{a}\bar{{\rm\Sigma}})$ be the canonical (![]() $G$-invariant) morphism. Then the following holds.
$G$-invariant) morphism. Then the following holds.
(1)
 $A$ is integral over
$A$ is integral over  $B$.
$B$.(2) The morphism
 $p$ is surjective, its fibers are
$p$ is surjective, its fibers are  $G$-orbits and the topology of
$G$-orbits and the topology of  $Y$ is the quotient of the topology of
$Y$ is the quotient of the topology of  $X$.
$X$.(3) Let
 $x\in X$,
$x\in X$,  $y=p(x)$. Write
$y=p(x)$. Write  $G_{x}$ for the stabilizer of
$G_{x}$ for the stabilizer of  $x$ and
$x$ and  ${\rm\Sigma}_{x}=\{{\it\sigma}\in {\rm\Sigma}:\text{}^{a}{\it\sigma}(x)=x\}$ (we used
${\rm\Sigma}_{x}=\{{\it\sigma}\in {\rm\Sigma}:\text{}^{a}{\it\sigma}(x)=x\}$ (we used  $\text{}^{a}{\rm\Sigma}_{x}=\text{}^{a}({\rm\Sigma}_{x})$ in 2.10). Let
$\text{}^{a}{\rm\Sigma}_{x}=\text{}^{a}({\rm\Sigma}_{x})$ in 2.10). Let  $\tilde{{\rm\Sigma}}_{x}=\{()^{{\it\sigma}}\in \tilde{{\rm\Sigma}}:{\it\sigma}\in {\rm\Sigma}_{x}\}$ and
$\tilde{{\rm\Sigma}}_{x}=\{()^{{\it\sigma}}\in \tilde{{\rm\Sigma}}:{\it\sigma}\in {\rm\Sigma}_{x}\}$ and  $\tilde{{\rm\Sigma}}^{x}=\{()^{{\it\sigma}^{x}}:{\it\sigma}\in {\rm\Sigma}_{x}\}$, where
$\tilde{{\rm\Sigma}}^{x}=\{()^{{\it\sigma}^{x}}:{\it\sigma}\in {\rm\Sigma}_{x}\}$, where  ${\it\sigma}^{x}:\mathbf{k}(x)\rightarrow \mathbf{k}(x)$ is induced by
${\it\sigma}^{x}:\mathbf{k}(x)\rightarrow \mathbf{k}(x)$ is induced by  ${\it\sigma}_{x}^{\sharp }:{\mathcal{O}}_{x}\rightarrow {\mathcal{O}}_{x}$ for every
${\it\sigma}_{x}^{\sharp }:{\mathcal{O}}_{x}\rightarrow {\mathcal{O}}_{x}$ for every  ${\it\sigma}\in {\rm\Sigma}_{x}$. Then
${\it\sigma}\in {\rm\Sigma}_{x}$. Then  $\mathbf{k}(x)$ is a quasi-Galois algebraic extension of
$\mathbf{k}(x)$ is a quasi-Galois algebraic extension of  $\mathbf{k}(y)$ and the canonical map is surjective.
$\mathbf{k}(y)$ and the canonical map is surjective. $$\begin{eqnarray}(G_{x},\tilde{{\rm\Sigma}}_{x})\rightarrow \left(\text{Gal}(\mathbf{k}(x)/\mathbf{k}(y)),\tilde{{\rm\Sigma}}^{x}\right)\end{eqnarray}$$
$$\begin{eqnarray}(G_{x},\tilde{{\rm\Sigma}}_{x})\rightarrow \left(\text{Gal}(\mathbf{k}(x)/\mathbf{k}(y)),\tilde{{\rm\Sigma}}^{x}\right)\end{eqnarray}$$(4) The natural homomorphism
 ${\mathcal{O}}_{Y}\rightarrow \left(p_{\ast }{\mathcal{O}}_{X}\right)^{G}$ is an isomorphism.
${\mathcal{O}}_{Y}\rightarrow \left(p_{\ast }{\mathcal{O}}_{X}\right)^{G}$ is an isomorphism.(5)
 $(Y,\bar{{\rm\Sigma}})$ is a quotient difference scheme of
$(Y,\bar{{\rm\Sigma}})$ is a quotient difference scheme of  $(X,{\rm\Sigma})$ by
$(X,{\rm\Sigma})$ by  $G$.
$G$.
Definition 2.23. Let ![]() $(X,{\rm\Sigma})$ be a difference scheme with a finite group of automorphisms
$(X,{\rm\Sigma})$ be a difference scheme with a finite group of automorphisms ![]() $(G,\tilde{{\rm\Sigma}})$ such that
$(G,\tilde{{\rm\Sigma}})$ such that 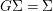 $G{\rm\Sigma}={\rm\Sigma}$ and let
$G{\rm\Sigma}={\rm\Sigma}$ and let 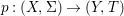 $p:(X,{\rm\Sigma})\rightarrow (Y,T)$ be an affine invariant morphism inducing
$p:(X,{\rm\Sigma})\rightarrow (Y,T)$ be an affine invariant morphism inducing 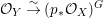 ${\mathcal{O}}_{Y}\stackrel{{\sim}}{\rightarrow }(p_{\ast }{\mathcal{O}}_{X})^{G}$. In this case, the morphism
${\mathcal{O}}_{Y}\stackrel{{\sim}}{\rightarrow }(p_{\ast }{\mathcal{O}}_{X})^{G}$. In this case, the morphism ![]() $p$ is called a Galois cover of
$p$ is called a Galois cover of ![]() $(Y,T)$ with group
$(Y,T)$ with group ![]() $(G,\tilde{{\rm\Sigma}})$.
$(G,\tilde{{\rm\Sigma}})$.
If ![]() $p$ is a Galois cover, it can be shown that
$p$ is a Galois cover, it can be shown that ![]() $(Y,T)$ is isomorphic to the quotient difference scheme
$(Y,T)$ is isomorphic to the quotient difference scheme 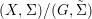 $(X,{\rm\Sigma})/(G,\tilde{{\rm\Sigma}})$ and the conclusions (1), (2), (3) of 2.22 still hold.
$(X,{\rm\Sigma})/(G,\tilde{{\rm\Sigma}})$ and the conclusions (1), (2), (3) of 2.22 still hold.
3 Local study of difference schemes and their morphisms
3.1 Difference schemes versus pro-algebraic varieties
One of the most important ideas in the study of difference algebraic geometry was the realization that there is a translation mechanism between the language of difference schemes and that of algebraic correspondences, or, more generally, systems of prolongations associated with a difference scheme.
We would like to be able to reduce the study of certain local properties of difference schemes to the study of known properties of algebraic schemes through systems of prolongations. In order to achieve this goal, we must be able to speak about difference subvarieties of ordinary algebraic varieties, which is achieved by defining a difference scheme associated to a scheme.
Proposition 3.1. [Reference Hrushovski18]
Let ![]() $(R,{\it\varsigma})$ be a difference ring. The forgetful functor from the category of difference
$(R,{\it\varsigma})$ be a difference ring. The forgetful functor from the category of difference ![]() $(R,{\it\varsigma})$-algebras to the category of
$(R,{\it\varsigma})$-algebras to the category of ![]() $R$-algebras has a left adjoint
$R$-algebras has a left adjoint ![]() $[{\it\varsigma}]_{R}$, that is, for every
$[{\it\varsigma}]_{R}$, that is, for every ![]() $R$-algebra
$R$-algebra ![]() $A$ we have a homomorphism
$A$ we have a homomorphism 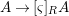 $A\rightarrow [{\it\varsigma}]_{R}A$ inducing the functorial isomorphism
$A\rightarrow [{\it\varsigma}]_{R}A$ inducing the functorial isomorphism
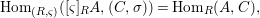 $$\begin{eqnarray}\text{Hom}_{(R,{\it\varsigma})}([{\it\varsigma}]_{R}A,(C,{\it\sigma}))=\text{Hom}_{R}(A,C),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{(R,{\it\varsigma})}([{\it\varsigma}]_{R}A,(C,{\it\sigma}))=\text{Hom}_{R}(A,C),\end{eqnarray}$$ for every ![]() $(R,{\it\varsigma})$-algebra
$(R,{\it\varsigma})$-algebra ![]() $(C,{\it\sigma})$.
$(C,{\it\sigma})$.
Proof. Let us write 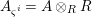 $A_{{\it\varsigma}^{i}}=A\otimes _{R}R$, where the morphism
$A_{{\it\varsigma}^{i}}=A\otimes _{R}R$, where the morphism ![]() $R\rightarrow R$ is
$R\rightarrow R$ is ![]() ${\it\varsigma}^{i}$, and let
${\it\varsigma}^{i}$, and let 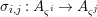 ${\it\sigma}_{i,j}:A_{{\it\varsigma}^{i}}\rightarrow A_{{\it\varsigma}^{j}}$ be the induced
${\it\sigma}_{i,j}:A_{{\it\varsigma}^{i}}\rightarrow A_{{\it\varsigma}^{j}}$ be the induced ![]() ${\it\varsigma}^{j-i}$-linear homomorphisms, for
${\it\varsigma}^{j-i}$-linear homomorphisms, for ![]() $i\leqslant j$. Writing
$i\leqslant j$. Writing
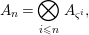 $$\begin{eqnarray}A_{n}=\mathop{\otimes }_{i\leqslant n}A_{{\it\varsigma}^{i}},\end{eqnarray}$$
$$\begin{eqnarray}A_{n}=\mathop{\otimes }_{i\leqslant n}A_{{\it\varsigma}^{i}},\end{eqnarray}$$ where the tensor product is taken over ![]() $R$, and
$R$, and
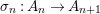 $$\begin{eqnarray}{\it\sigma}_{n}:A_{n}\rightarrow A_{n+1}\end{eqnarray}$$
$$\begin{eqnarray}{\it\sigma}_{n}:A_{n}\rightarrow A_{n+1}\end{eqnarray}$$ for the natural ![]() ${\it\varsigma}$-homomorphisms induced by the
${\it\varsigma}$-homomorphisms induced by the ![]() ${\it\sigma}_{i,i+1}$, we obtain a system
${\it\sigma}_{i,i+1}$, we obtain a system ![]() $A_{n}$ of
$A_{n}$ of ![]() $R$-algebras directed by inclusions
$R$-algebras directed by inclusions 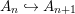 $A_{n}{\hookrightarrow}A_{n+1}$. The direct limit
$A_{n}{\hookrightarrow}A_{n+1}$. The direct limit 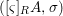 $([{\it\varsigma}]_{R}A,{\it\sigma})$ of
$([{\it\varsigma}]_{R}A,{\it\sigma})$ of ![]() $A_{n}$ and
$A_{n}$ and ![]() ${\it\sigma}_{n}$ is clearly a difference
${\it\sigma}_{n}$ is clearly a difference ![]() $(R,{\it\varsigma})$-algebra, and the inclusion
$(R,{\it\varsigma})$-algebra, and the inclusion 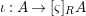 ${\it\iota}:A\rightarrow [{\it\varsigma}]_{R}A$ is obtained by identifying
${\it\iota}:A\rightarrow [{\it\varsigma}]_{R}A$ is obtained by identifying ![]() $A$ with
$A$ with ![]() $A_{0}$.
$A_{0}$.
We need to show that every ![]() $R$-homomorphism
$R$-homomorphism 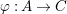 ${\it\varphi}:A\rightarrow C$ to an
${\it\varphi}:A\rightarrow C$ to an ![]() $(R,{\it\varsigma})$-algebra
$(R,{\it\varsigma})$-algebra ![]() $(C,{\it\sigma})$ lifts uniquely to a
$(C,{\it\sigma})$ lifts uniquely to a ![]() $(R,{\it\varsigma})$-homomorphism
$(R,{\it\varsigma})$-homomorphism 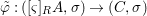 $\tilde{{\it\varphi}}:([{\it\varsigma}]_{R}A,{\it\sigma})\rightarrow (C,{\it\sigma})$ such that
$\tilde{{\it\varphi}}:([{\it\varsigma}]_{R}A,{\it\sigma})\rightarrow (C,{\it\sigma})$ such that ![]() ${\it\varphi}=\tilde{{\it\varphi}}{\it\iota}$. By the universal property of tensor products, the diagram
${\it\varphi}=\tilde{{\it\varphi}}{\it\iota}$. By the universal property of tensor products, the diagram
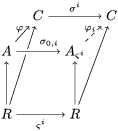
yields a unique 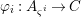 ${\it\varphi}_{i}:A_{{\it\varsigma}^{i}}\rightarrow C$, and subsequently
${\it\varphi}_{i}:A_{{\it\varsigma}^{i}}\rightarrow C$, and subsequently 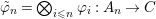 $\tilde{{\it\varphi}}_{n}=\otimes _{i\leqslant n}{\it\varphi}_{i}:A_{n}\rightarrow C$. Passing to the limit, we obtain
$\tilde{{\it\varphi}}_{n}=\otimes _{i\leqslant n}{\it\varphi}_{i}:A_{n}\rightarrow C$. Passing to the limit, we obtain 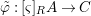 $\tilde{{\it\varphi}}:[{\it\varsigma}]_{R}A\rightarrow C$ with the required properties.◻
$\tilde{{\it\varphi}}:[{\it\varsigma}]_{R}A\rightarrow C$ with the required properties.◻
Proposition 3.2. [Reference Hrushovski18]
Let ![]() $(R,{\it\varsigma})$ be a difference ring and let
$(R,{\it\varsigma})$ be a difference ring and let ![]() $X$ be an (algebraic) scheme over
$X$ be an (algebraic) scheme over ![]() $R$. The functor from the category of difference
$R$. The functor from the category of difference ![]() $(R,{\it\varsigma})$-schemes to the category of sets,
$(R,{\it\varsigma})$-schemes to the category of sets, 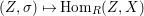 $(Z,{\it\sigma})\mapsto \text{Hom}_{R}(Z,X)$ (morphisms of locally
$(Z,{\it\sigma})\mapsto \text{Hom}_{R}(Z,X)$ (morphisms of locally ![]() $R$-ringed spaces) is representable. More precisely, the universal morphism
$R$-ringed spaces) is representable. More precisely, the universal morphism 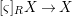 $[{\it\varsigma}]_{R}X\rightarrow X$ of locally
$[{\it\varsigma}]_{R}X\rightarrow X$ of locally ![]() $R$-ringed spaces induces a functorial isomorphism
$R$-ringed spaces induces a functorial isomorphism
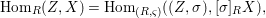 $$\begin{eqnarray}\text{Hom}_{R}(Z,X)=\text{Hom}_{(R,{\it\varsigma})}((Z,{\it\sigma}),[{\it\sigma}]_{R}X),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{R}(Z,X)=\text{Hom}_{(R,{\it\varsigma})}((Z,{\it\sigma}),[{\it\sigma}]_{R}X),\end{eqnarray}$$ for every ![]() $(R,{\it\sigma})$-difference scheme
$(R,{\it\sigma})$-difference scheme ![]() $(Z,{\it\sigma})$.
$(Z,{\it\sigma})$.
Proof. Let us prove the affine case. Suppose 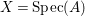 $X=\text{Spec}(A)$,
$X=\text{Spec}(A)$, 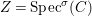 $Z=\text{Spec}^{{\it\sigma}}(C)$ for a well-mixed difference ring
$Z=\text{Spec}^{{\it\sigma}}(C)$ for a well-mixed difference ring ![]() $(C,{\it\sigma})$ and let
$(C,{\it\sigma})$ and let 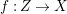 $f:Z\rightarrow X$ be a morphism of locally ringed spaces. By taking global sections of the corresponding sheaf morphism, we derive a ring homomorphism
$f:Z\rightarrow X$ be a morphism of locally ringed spaces. By taking global sections of the corresponding sheaf morphism, we derive a ring homomorphism 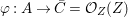 ${\it\varphi}:A\rightarrow \bar{C}={\mathcal{O}}_{Z}(Z)$ so that, in view of 2.8
${\it\varphi}:A\rightarrow \bar{C}={\mathcal{O}}_{Z}(Z)$ so that, in view of 2.8 ![]() $f$ is the restriction of
$f$ is the restriction of 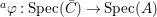 $\text{}^{a}{\it\varphi}:\text{Spec}(\bar{C})\rightarrow \text{Spec}(A)$ to
$\text{}^{a}{\it\varphi}:\text{Spec}(\bar{C})\rightarrow \text{Spec}(A)$ to 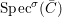 $\text{Spec}^{{\it\sigma}}(\bar{C})$. Using 3.1, there is a unique lift
$\text{Spec}^{{\it\sigma}}(\bar{C})$. Using 3.1, there is a unique lift 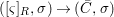 $([{\it\varsigma}]_{R},{\it\sigma})\rightarrow (\bar{C},{\it\sigma})$ of
$([{\it\varsigma}]_{R},{\it\sigma})\rightarrow (\bar{C},{\it\sigma})$ of ![]() ${\it\varphi}$, which gives the required difference scheme morphism
${\it\varphi}$, which gives the required difference scheme morphism
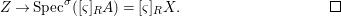 $$\begin{eqnarray}Z\rightarrow \text{Spec}^{{\it\sigma}}([{\it\varsigma}]_{R}A)=[{\it\varsigma}]_{R}X.\end{eqnarray}$$
$$\begin{eqnarray}Z\rightarrow \text{Spec}^{{\it\sigma}}([{\it\varsigma}]_{R}A)=[{\it\varsigma}]_{R}X.\end{eqnarray}$$ Suppose now that ![]() $X$ is an
$X$ is an ![]() $R$-scheme and
$R$-scheme and ![]() $(Z,{\it\sigma})$ is a closed
$(Z,{\it\sigma})$ is a closed ![]() $(R,{\it\varsigma})$-difference subscheme of
$(R,{\it\varsigma})$-difference subscheme of ![]() $[{\it\varsigma}]_{R}X$. For ease of notation, let us write
$[{\it\varsigma}]_{R}X$. For ease of notation, let us write 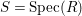 $S=\text{Spec}(R)$. Writing
$S=\text{Spec}(R)$. Writing ![]() $X_{{\it\varsigma}^{i}}$ for the base change
$X_{{\it\varsigma}^{i}}$ for the base change  $X\times _{S}S$ via the morphism
$X\times _{S}S$ via the morphism  ${\it\varsigma}^{i}:S\rightarrow S$, it is clear that the
${\it\varsigma}^{i}:S\rightarrow S$, it is clear that the ![]() ${\it\varsigma}^{i}$-linear morphism
${\it\varsigma}^{i}$-linear morphism 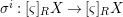 ${\it\sigma}^{i}:[{\it\varsigma}]_{R}X\rightarrow [{\it\varsigma}]_{R}X$ defines an
${\it\sigma}^{i}:[{\it\varsigma}]_{R}X\rightarrow [{\it\varsigma}]_{R}X$ defines an ![]() $R$-morphism
$R$-morphism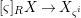 $[{\it\varsigma}]_{R}X\rightarrow X_{{\it\varsigma}^{i}}$ and thus we deduce a morphism
$[{\it\varsigma}]_{R}X\rightarrow X_{{\it\varsigma}^{i}}$ and thus we deduce a morphism
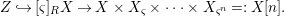 $$\begin{eqnarray}Z{\hookrightarrow}[{\it\varsigma}]_{R}X\rightarrow X\times X_{{\it\varsigma}}\times \cdots \times X_{{\it\varsigma}^{n}}=:X[n].\end{eqnarray}$$
$$\begin{eqnarray}Z{\hookrightarrow}[{\it\varsigma}]_{R}X\rightarrow X\times X_{{\it\varsigma}}\times \cdots \times X_{{\it\varsigma}^{n}}=:X[n].\end{eqnarray}$$ We denote the scheme-theoretic image of this map by ![]() $Z[n]$, obtaining a closed
$Z[n]$, obtaining a closed ![]() $R$-subscheme
$R$-subscheme 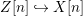 $Z[n]{\hookrightarrow}X[n]$ for every
$Z[n]{\hookrightarrow}X[n]$ for every ![]() $n$, called the
$n$, called the ![]() $n\text{th}$Zariski closure of the difference scheme
$n\text{th}$Zariski closure of the difference scheme ![]() $Z$in
$Z$in ![]() $X$. Although the projective limit
$X$. Although the projective limit ![]() $Z[\infty ]$ of the
$Z[\infty ]$ of the ![]() $Z[n]$ can be viewed as a scheme, we find it most illuminating to view it as a pro-(scheme of finite type).
$Z[n]$ can be viewed as a scheme, we find it most illuminating to view it as a pro-(scheme of finite type).
The maps 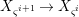 $X_{{\it\varsigma}^{i+1}}\rightarrow X_{{\it\varsigma}^{i}}$ induce the maps
$X_{{\it\varsigma}^{i+1}}\rightarrow X_{{\it\varsigma}^{i}}$ induce the maps 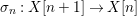 ${\it\sigma}_{n}:X[n+1]\rightarrow X[n]$ and thus
${\it\sigma}_{n}:X[n+1]\rightarrow X[n]$ and thus ![]() $X[\infty ]$ is equipped with an endomorphism
$X[\infty ]$ is equipped with an endomorphism ![]() ${\it\sigma}$, which is the limit of
${\it\sigma}$, which is the limit of ![]() ${\it\sigma}_{n}$. In this context,
${\it\sigma}_{n}$. In this context, ![]() $[{\it\varsigma}]_{R}X$ is the fixed-point scheme of
$[{\it\varsigma}]_{R}X$ is the fixed-point scheme of ![]() ${\it\sigma}$ on
${\it\sigma}$ on ![]() $X[\infty ]$.
$X[\infty ]$.
We say that ![]() $Z$ is weakly Zariski dense in
$Z$ is weakly Zariski dense in ![]() $X$ if
$X$ if 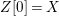 $Z[0]=X$. Note that it can happen that
$Z[0]=X$. Note that it can happen that ![]() $Z$ is weakly Zariski dense in
$Z$ is weakly Zariski dense in ![]() $X$ but the set of points of
$X$ but the set of points of ![]() $Z$ is not Zariski dense in
$Z$ is not Zariski dense in ![]() $X$.
$X$.
Let us now start with a difference scheme ![]() $(X,{\it\sigma})$ of finite
$(X,{\it\sigma})$ of finite ![]() ${\it\sigma}$-type over
${\it\sigma}$-type over ![]() $(R,{\it\varsigma})$ and build a system of “prolongations” of
$(R,{\it\varsigma})$ and build a system of “prolongations” of ![]() $X$ in which
$X$ in which ![]() $X$ is weakly Zariski dense by construction. We shall describe the procedure for an affine difference scheme
$X$ is weakly Zariski dense by construction. We shall describe the procedure for an affine difference scheme 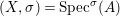 $(X,{\it\sigma})=\text{Spec}^{{\it\sigma}}(A)$, where
$(X,{\it\sigma})=\text{Spec}^{{\it\sigma}}(A)$, where 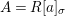 $A=R[a]_{{\it\sigma}}$ is an
$A=R[a]_{{\it\sigma}}$ is an ![]() $(R,{\it\varsigma})$-algebra of finite
$(R,{\it\varsigma})$-algebra of finite ![]() ${\it\sigma}$-type, generated by a tuple
${\it\sigma}$-type, generated by a tuple ![]() $a\in A$.
$a\in A$.
If we write 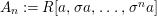 $A_{n}:=R[a,{\it\sigma}a,\ldots ,{\it\sigma}^{n}a]$, we have inclusions
$A_{n}:=R[a,{\it\sigma}a,\ldots ,{\it\sigma}^{n}a]$, we have inclusions 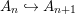 $A_{n}{\hookrightarrow}A_{n+1}$ and maps
$A_{n}{\hookrightarrow}A_{n+1}$ and maps 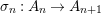 ${\it\sigma}_{n}:A_{n}\rightarrow A_{n+1}$ induced by
${\it\sigma}_{n}:A_{n}\rightarrow A_{n+1}$ induced by ![]() ${\it\sigma}$, so that
${\it\sigma}$, so that ![]() $(A,{\it\sigma})$ is the direct limit of the
$(A,{\it\sigma})$ is the direct limit of the ![]() $A_{n}$ and the
$A_{n}$ and the ![]() ${\it\sigma}_{n}$. We obtain the following diagram for
${\it\sigma}_{n}$. We obtain the following diagram for 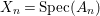 $X_{n}=\text{Spec}(A_{n})$.
$X_{n}=\text{Spec}(A_{n})$.
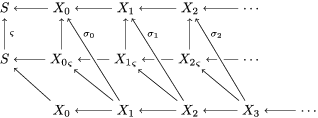
By construction, we have closed immersions 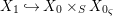 $X_{1}{\hookrightarrow}X_{0}\times _{S}{X_{0}}_{{\it\varsigma}}$ and
$X_{1}{\hookrightarrow}X_{0}\times _{S}{X_{0}}_{{\it\varsigma}}$ and 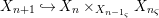 $X_{n+1}{\hookrightarrow}X_{n}\times _{{X_{n-1}}_{{\it\varsigma}}}{X_{n}}_{{\it\varsigma}}$ for
$X_{n+1}{\hookrightarrow}X_{n}\times _{{X_{n-1}}_{{\it\varsigma}}}{X_{n}}_{{\it\varsigma}}$ for ![]() $n\geqslant 1$, and we conclude that we have written
$n\geqslant 1$, and we conclude that we have written ![]() $(X,{\it\sigma})$ as a weakly Zariski dense difference subscheme of
$(X,{\it\sigma})$ as a weakly Zariski dense difference subscheme of ![]() $X_{0}$.
$X_{0}$.
Lemma 3.3. (Preparation Lemma)
With above notation, if ![]() $A$ and
$A$ and ![]() $R$ are transformally integral, by
$R$ are transformally integral, by ![]() ${\it\sigma}$-localizing
${\it\sigma}$-localizing ![]() $A$ and
$A$ and ![]() $R$ we can arrange that morphisms
$R$ we can arrange that morphisms
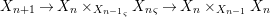 $$\begin{eqnarray}X_{n+1}\rightarrow X_{n}\times _{{X_{n-1}}_{{\it\varsigma}}}{X_{n}}_{{\it\varsigma}}\rightarrow X_{n}\times _{X_{n-1}}X_{n}\end{eqnarray}$$
$$\begin{eqnarray}X_{n+1}\rightarrow X_{n}\times _{{X_{n-1}}_{{\it\varsigma}}}{X_{n}}_{{\it\varsigma}}\rightarrow X_{n}\times _{X_{n-1}}X_{n}\end{eqnarray}$$ are isomorphisms for ![]() $n\geqslant 1$ and that
$n\geqslant 1$ and that ![]() $X$ is a Zariski dense difference subscheme of
$X$ is a Zariski dense difference subscheme of ![]() $X_{0}$.
$X_{0}$.
Proof. Let ![]() $K$ be the fraction field of
$K$ be the fraction field of ![]() $R$. By combining the statements 5.2.10, 5.2.11, 5.2.12 from [Reference Levin20], modulo a
$R$. By combining the statements 5.2.10, 5.2.11, 5.2.12 from [Reference Levin20], modulo a ![]() ${\it\varsigma}$-localization of
${\it\varsigma}$-localization of ![]() $R$, we can find a new tuple of generators
$R$, we can find a new tuple of generators ![]() $a=bc$ so that, writing
$a=bc$ so that, writing 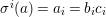 ${\it\sigma}^{i}(a)=a_{i}=b_{i}c_{i}$ and
${\it\sigma}^{i}(a)=a_{i}=b_{i}c_{i}$ and 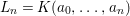 $L_{n}=K(a_{0},\ldots ,a_{n})$ for the fraction field of
$L_{n}=K(a_{0},\ldots ,a_{n})$ for the fraction field of ![]() $A_{n}$, we have that for
$A_{n}$, we have that for ![]() $n\geqslant 1$,
$n\geqslant 1$,
(1)
 $b_{n}$ is algebraically independent over
$b_{n}$ is algebraically independent over  $L_{n-1}$; and
$L_{n-1}$; and(2)
 $[L_{n}:L_{n-1}(b_{n})]=[L_{n+1}:L_{n}(b_{n+1})]$.
$[L_{n}:L_{n-1}(b_{n})]=[L_{n+1}:L_{n}(b_{n+1})]$.
Given a diagram
of sub-![]() $k$-algebras
$k$-algebras ![]() $B$,
$B$, ![]() $C$ of a difference field
$C$ of a difference field ![]() $(K,{\it\sigma})$, we shall say that
$(K,{\it\sigma})$, we shall say that ![]() $B$ is
$B$ is ![]() ${\it\sigma}$-linearly disjoint from
${\it\sigma}$-linearly disjoint from ![]() $C$ over
$C$ over ![]() $k$ if whenever
$k$ if whenever 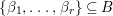 $\{{\it\beta}_{1},\ldots ,{\it\beta}_{r}\}\subseteq B$ is linearly independent over
$\{{\it\beta}_{1},\ldots ,{\it\beta}_{r}\}\subseteq B$ is linearly independent over ![]() $k$, then
$k$, then 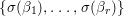 $\{{\it\sigma}({\it\beta}_{1}),\ldots ,{\it\sigma}({\it\beta}_{r})\}$ is linearly independent over
$\{{\it\sigma}({\it\beta}_{1}),\ldots ,{\it\sigma}({\it\beta}_{r})\}$ is linearly independent over ![]() $C$. This is equivalent to the injectivity of the natural map
$C$. This is equivalent to the injectivity of the natural map 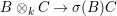 $B\otimes _{k}C\rightarrow {\it\sigma}(B)C$.
$B\otimes _{k}C\rightarrow {\it\sigma}(B)C$.
Using (1), we see that 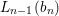 $L_{n-1}(b_{n})$ is
$L_{n-1}(b_{n})$ is ![]() ${\it\sigma}$-linearly disjoint from
${\it\sigma}$-linearly disjoint from ![]() $L_{n}$ over
$L_{n}$ over ![]() $L_{n-1}$, and using (2) we deduce that
$L_{n-1}$, and using (2) we deduce that ![]() $L_{n}$ is
$L_{n}$ is ![]() ${\it\sigma}$-linearly disjoint from
${\it\sigma}$-linearly disjoint from 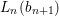 $L_{n}(b_{n+1})$ over
$L_{n}(b_{n+1})$ over 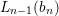 $L_{n-1}(b_{n})$. By transitivity of
$L_{n-1}(b_{n})$. By transitivity of ![]() ${\it\sigma}$-linear disjointness, it follows from the diagram
${\it\sigma}$-linear disjointness, it follows from the diagram

that ![]() $L_{n}$ is
$L_{n}$ is ![]() ${\it\sigma}$-linearly disjoint from
${\it\sigma}$-linearly disjoint from ![]() $L_{n}$ over
$L_{n}$ over ![]() $L_{n-1}$ for all
$L_{n-1}$ for all ![]() $n\geqslant 1$.
$n\geqslant 1$.
Now, using generic flatness [Reference Grothendieck16, Théorème 6.9.2], by ![]() ${\it\sigma}$-localizing
${\it\sigma}$-localizing ![]() $A$ (by an element of
$A$ (by an element of ![]() $A_{0}$) we may assume that
$A_{0}$) we may assume that 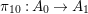 ${\it\pi}_{10}:A_{0}\rightarrow A_{1}$ and
${\it\pi}_{10}:A_{0}\rightarrow A_{1}$ and 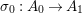 ${\it\sigma}_{0}:A_{0}\rightarrow A_{1}$ are flat (i.e.,
${\it\sigma}_{0}:A_{0}\rightarrow A_{1}$ are flat (i.e., ![]() $A_{1}$ is a flat
$A_{1}$ is a flat ![]() $A_{0}$-module both via
$A_{0}$-module both via ![]() ${\it\pi}_{10}$ and
${\it\pi}_{10}$ and ![]() ${\it\sigma}_{0}$), so
${\it\sigma}_{0}$), so 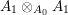 $A_{1}\otimes _{A_{0}}A_{1}$ is a flat
$A_{1}\otimes _{A_{0}}A_{1}$ is a flat ![]() $A_{0}$ module. Thus the natural morphism
$A_{0}$ module. Thus the natural morphism
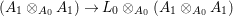 $$\begin{eqnarray}(A_{1}\otimes _{A_{0}}A_{1})\rightarrow L_{0}\otimes _{A_{0}}(A_{1}\otimes _{A_{0}}A_{1})\end{eqnarray}$$
$$\begin{eqnarray}(A_{1}\otimes _{A_{0}}A_{1})\rightarrow L_{0}\otimes _{A_{0}}(A_{1}\otimes _{A_{0}}A_{1})\end{eqnarray}$$ is injective, the kernel in general being the ![]() $A_{0}$-torsion of
$A_{0}$-torsion of 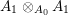 $A_{1}\otimes _{A_{0}}A_{1}$, which we thoughtfully made trivial. Moreover, by linear disjointness guaranteed by the construction,
$A_{1}\otimes _{A_{0}}A_{1}$, which we thoughtfully made trivial. Moreover, by linear disjointness guaranteed by the construction,
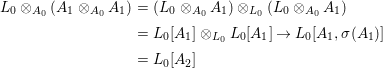 $$\begin{eqnarray}\displaystyle L_{0}\otimes _{A_{0}}(A_{1}\otimes _{A_{0}}A_{1}) & = & \displaystyle (L_{0}\otimes _{A_{0}}A_{1})\otimes _{L_{0}}(L_{0}\otimes _{A_{0}}A_{1})\nonumber\\ \displaystyle & = & \displaystyle L_{0}[A_{1}]\otimes _{L_{0}}L_{0}[A_{1}]\rightarrow L_{0}[A_{1},{\it\sigma}(A_{1})]\nonumber\\ \displaystyle & = & \displaystyle L_{0}[A_{2}]\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{0}\otimes _{A_{0}}(A_{1}\otimes _{A_{0}}A_{1}) & = & \displaystyle (L_{0}\otimes _{A_{0}}A_{1})\otimes _{L_{0}}(L_{0}\otimes _{A_{0}}A_{1})\nonumber\\ \displaystyle & = & \displaystyle L_{0}[A_{1}]\otimes _{L_{0}}L_{0}[A_{1}]\rightarrow L_{0}[A_{1},{\it\sigma}(A_{1})]\nonumber\\ \displaystyle & = & \displaystyle L_{0}[A_{2}]\nonumber\end{eqnarray}$$ is injective. We conclude that 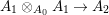 $A_{1}\otimes _{A_{0}}A_{1}\rightarrow A_{2}$ is injective and thus bijective by the construction, and that both
$A_{1}\otimes _{A_{0}}A_{1}\rightarrow A_{2}$ is injective and thus bijective by the construction, and that both 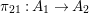 ${\it\pi}_{21}:A_{1}\rightarrow A_{2}$ and
${\it\pi}_{21}:A_{1}\rightarrow A_{2}$ and 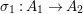 ${\it\sigma}_{1}:A_{1}\rightarrow A_{2}$ are flat. This is all we need to proceed by induction and prove that all
${\it\sigma}_{1}:A_{1}\rightarrow A_{2}$ are flat. This is all we need to proceed by induction and prove that all
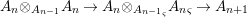 $$\begin{eqnarray}A_{n}\otimes _{A_{n-1}}A_{n}\rightarrow A_{n}\otimes _{{A_{n-1}}_{{\it\varsigma}}}{A_{n}}_{{\it\varsigma}}\rightarrow A_{n+1}\end{eqnarray}$$
$$\begin{eqnarray}A_{n}\otimes _{A_{n-1}}A_{n}\rightarrow A_{n}\otimes _{{A_{n-1}}_{{\it\varsigma}}}{A_{n}}_{{\it\varsigma}}\rightarrow A_{n+1}\end{eqnarray}$$ are isomorphisms. Note, if we are happy to finish with the associated morphisms being just closed immersions which are generically isomorphisms, we can skip the “generic flatness” step and we do not need to localize ![]() $A$ but only
$A$ but only ![]() $R$.◻
$R$.◻
Definition 3.4. Let ![]() $P$ be a property of scheme morphisms of finite type. Consider the following permanence properties of
$P$ be a property of scheme morphisms of finite type. Consider the following permanence properties of ![]() $P$:
$P$:
(1) (Composite). A composite of morphisms with property
 $P$ has property
$P$ has property  $P$.
$P$.(2) (Base change). If
 $X\rightarrow Y$ has
$X\rightarrow Y$ has  $P$, and
$P$, and  $Z\rightarrow Y$ is arbitrary, then the morphism
$Z\rightarrow Y$ is arbitrary, then the morphism  $X\times _{Y}Z\rightarrow Z$ has
$X\times _{Y}Z\rightarrow Z$ has  $P$.
$P$.(3) (Open embedding). If
 $X\rightarrow Y$ has
$X\rightarrow Y$ has  $P$, and
$P$, and  $U{\hookrightarrow}X$, then
$U{\hookrightarrow}X$, then  $U\rightarrow Y$ has
$U\rightarrow Y$ has  $P$.
$P$.(4) (Genericity in the target). If
 $f:X\rightarrow Y$ (with
$f:X\rightarrow Y$ (with  $Y$ integral) is generically
$Y$ integral) is generically  $P$, there is a localization
$P$, there is a localization  $Y^{\prime }$ of
$Y^{\prime }$ of  $Y$ such that
$Y$ such that  $f\,\restriction\,f^{-1}(Y^{\prime })$ is
$f\,\restriction\,f^{-1}(Y^{\prime })$ is  $P$.
$P$.
- (
 $4^{\prime }$)
$4^{\prime }$) (Genericity in the source). If
 $f:X\rightarrow Y$ (with
$f:X\rightarrow Y$ (with  $Y$ integral) is generically
$Y$ integral) is generically  $P$, there is a localization
$P$, there is a localization  $X^{\prime }$ of
$X^{\prime }$ of  $X$ and
$X$ and  $Y^{\prime }$ of
$Y^{\prime }$ of  $Y$ such that the morphism
$Y$ such that the morphism  $f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is
$f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is  $P$.
$P$.
We say that ![]() $P$ is hereditary if it has properties (1)–(3). It is hereditarily generic in the target (resp. source), if it is hereditary with property (4) (resp. (4’)). The property
$P$ is hereditary if it has properties (1)–(3). It is hereditarily generic in the target (resp. source), if it is hereditary with property (4) (resp. (4’)). The property ![]() $P$ is strongly hereditary if in addition,
$P$ is strongly hereditary if in addition,
(5) (SH). If
 $g\circ f$ and
$g\circ f$ and  $g$ have
$g$ have  $P$, then
$P$, then  $f$ has
$f$ has  $P$.
$P$.
(1) Let
 $(X,{\it\sigma})$ be an
$(X,{\it\sigma})$ be an  $(R,{\it\sigma})$-difference scheme of finite
$(R,{\it\sigma})$-difference scheme of finite  ${\it\sigma}$-type. We say that
${\it\sigma}$-type. We say that  $(X,{\it\sigma})$ has the property
$(X,{\it\sigma})$ has the property  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, if there exists a prolongation sequence
$P$, if there exists a prolongation sequence  $X_{n}$ as above for
$X_{n}$ as above for  $X$ such that all the structure maps
$X$ such that all the structure maps  $X_{n}\rightarrow \text{Spec}(R)$ have the property
$X_{n}\rightarrow \text{Spec}(R)$ have the property  $P$.
$P$.(2) Let
 $P$ be a property of scheme morphisms of finite type. Let
$P$ be a property of scheme morphisms of finite type. Let  $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of finite
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of finite  ${\it\sigma}$-type. We say that
${\it\sigma}$-type. We say that  $f$ has the property
$f$ has the property  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, if for every open affine
$P$, if for every open affine  $V=\text{Spec}^{{\it\sigma}}(R)$ in
$V=\text{Spec}^{{\it\sigma}}(R)$ in  $Y$, the scheme
$Y$, the scheme  $f^{-1}(V)$ has the property
$f^{-1}(V)$ has the property  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$.
$P$.(3) Let
 $P$ be a property of morphisms of schemes of finite type. Let
$P$ be a property of morphisms of schemes of finite type. Let  $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of schemes of finite
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of schemes of finite  ${\it\sigma}$-type (over a common base). We say that
${\it\sigma}$-type (over a common base). We say that  $f$ has the property
$f$ has the property  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, if there exists a prolongation sequence
$P$, if there exists a prolongation sequence  $f_{n}:X_{n}\rightarrow Y_{n}$ for
$f_{n}:X_{n}\rightarrow Y_{n}$ for  $f$ such that all the maps
$f$ such that all the maps  $f_{n}$ have the property
$f_{n}$ have the property  $P$.
$P$.
Remark 3.6. Suppose ![]() $P$ is strongly hereditary.
$P$ is strongly hereditary.
(1) If
 $(X,{\it\sigma})$ is
$(X,{\it\sigma})$ is  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, then all the connecting morphisms
$P$, then all the connecting morphisms  $X_{n+1}\rightarrow X_{n}$ have the property
$X_{n+1}\rightarrow X_{n}$ have the property  $P$.
$P$.(2) If a morphism
 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ of schemes of finite
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ of schemes of finite  ${\it\sigma}$-type (over some common base) is
${\it\sigma}$-type (over some common base) is  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, and
$P$, and  $(Y,{\it\sigma})$ is
$(Y,{\it\sigma})$ is  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, then
$P$, then  $(X,{\it\sigma})$ is
$(X,{\it\sigma})$ is  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$.
$P$.
(1) Let
 $P$ be a property of scheme morphisms of finite type which is hereditarily generic in the source/target. Then the property
$P$ be a property of scheme morphisms of finite type which is hereditarily generic in the source/target. Then the property  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$ is
$P$ is  ${\it\sigma}$-generic in the source. In other words, if
${\it\sigma}$-generic in the source. In other words, if  $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is a morphism of finite
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is a morphism of finite  ${\it\sigma}$-type between transformally integral schemes which is generically
${\it\sigma}$-type between transformally integral schemes which is generically  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, then there exists a
$P$, then there exists a  ${\it\sigma}$-localization
${\it\sigma}$-localization  $X^{\prime }$ of
$X^{\prime }$ of  $X$ and
$X$ and  $Y^{\prime }$ of
$Y^{\prime }$ of  $Y$ such that
$Y$ such that  $f\,\restriction\,X^{\prime }$ is
$f\,\restriction\,X^{\prime }$ is  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$ above
$P$ above  $Y^{\prime }$, that is,
$Y^{\prime }$, that is,  $f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is
$f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$.
$P$.(2) The same statement applies when
 $P$ is a (target/source) hereditarily generic property of morphisms of schemes of finite type and
$P$ is a (target/source) hereditarily generic property of morphisms of schemes of finite type and  $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is a morphism of transformally integral schemes of finite
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is a morphism of transformally integral schemes of finite  ${\it\sigma}$-type.
${\it\sigma}$-type.
Proof. Let us prove (2), the proof of (1) being strictly easier. We shall assume the reader has constructed, upon a ![]() ${\it\sigma}$-localization of the source, the relevant diagram of prolongations for
${\it\sigma}$-localization of the source, the relevant diagram of prolongations for 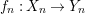 $f_{n}:X_{n}\rightarrow Y_{n}$ using the Preparation Lemma 3.3. In the case of genericity in the target, by using (G), modulo a
$f_{n}:X_{n}\rightarrow Y_{n}$ using the Preparation Lemma 3.3. In the case of genericity in the target, by using (G), modulo a ![]() ${\it\sigma}$-localization of
${\it\sigma}$-localization of ![]() $Y$ we can assume that
$Y$ we can assume that 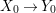 $X_{0}\rightarrow Y_{0}$ has
$X_{0}\rightarrow Y_{0}$ has ![]() $P$. Using (G) and (O), by
$P$. Using (G) and (O), by ![]() ${\it\sigma}$-localizing
${\it\sigma}$-localizing ![]() $X$ by an element of
$X$ by an element of ![]() $X_{0}$ we can assume that
$X_{0}$ we can assume that 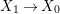 $X_{1}\rightarrow X_{0}$ also has
$X_{1}\rightarrow X_{0}$ also has ![]() $P$.
$P$.
In the case of genericity in the source, using (G), by a ![]() ${\it\sigma}$-localization of
${\it\sigma}$-localization of ![]() $X$ and
$X$ and ![]() $Y$ we can assume that
$Y$ we can assume that 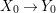 $X_{0}\rightarrow Y_{0}$ has
$X_{0}\rightarrow Y_{0}$ has ![]() $P$. Using (G) again, we need to
$P$. Using (G) again, we need to ![]() ${\it\sigma}$-localize
${\it\sigma}$-localize ![]() $X$ further to make
$X$ further to make 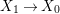 $X_{1}\rightarrow X_{0}$ have the property
$X_{1}\rightarrow X_{0}$ have the property ![]() $P$. Using (O), the new
$P$. Using (O), the new 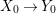 $X_{0}\rightarrow Y_{0}$ still has
$X_{0}\rightarrow Y_{0}$ still has ![]() $P$, but we lose the exact
$P$, but we lose the exact ![]() ${\it\sigma}$-generation in terms of fiber products to the extent that
${\it\sigma}$-generation in terms of fiber products to the extent that  $X_{n+1}\rightarrow X_{n}\times _{{X_{n-1}}_{{\it\varsigma}}}{X_{n}}_{{\it\varsigma}}$ are no longer isomorphisms for
$X_{n+1}\rightarrow X_{n}\times _{{X_{n-1}}_{{\it\varsigma}}}{X_{n}}_{{\it\varsigma}}$ are no longer isomorphisms for ![]() $n\geqslant 1$, but only open immersions.
$n\geqslant 1$, but only open immersions.
We proceed by induction. Assuming that  $X_{n-1}\rightarrow Y_{n-1}$ and
$X_{n-1}\rightarrow Y_{n-1}$ and 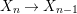 $X_{n}\rightarrow X_{n-1}$ have
$X_{n}\rightarrow X_{n-1}$ have ![]() $P$, using (C), we get that
$P$, using (C), we get that 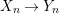 $X_{n}\rightarrow Y_{n}$ has
$X_{n}\rightarrow Y_{n}$ has ![]() $P$. Moreover, using (BC), we obtain that
$P$. Moreover, using (BC), we obtain that 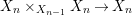 $X_{n}\times _{X_{n-1}}X_{n}\rightarrow X_{n}$ has
$X_{n}\times _{X_{n-1}}X_{n}\rightarrow X_{n}$ has ![]() $P$. By (O) and the fact that
$P$. By (O) and the fact that 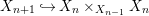 $X_{n+1}{\hookrightarrow}X_{n}\times _{X_{n-1}}X_{n}$ for
$X_{n+1}{\hookrightarrow}X_{n}\times _{X_{n-1}}X_{n}$ for ![]() $n\geqslant 1$, we can deduce that
$n\geqslant 1$, we can deduce that 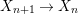 $X_{n+1}\rightarrow X_{n}$ also has
$X_{n+1}\rightarrow X_{n}$ also has ![]() $P$, which keeps the induction going.
$P$, which keeps the induction going.
Let us note that, in case of a property strongly hereditarily generic in the target, if the preparation lemma could be improved so that we need only localize the base, then we could prove that ![]() ${\it\sigma}$-pro-
${\it\sigma}$-pro-![]() $P$ is
$P$ is ![]() ${\it\sigma}$-generic in the target.◻
${\it\sigma}$-generic in the target.◻
Corollary 3.8. Let 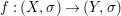 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of finite
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of finite ![]() ${\it\sigma}$-type between transformally integral schemes.
${\it\sigma}$-type between transformally integral schemes.
(1) If
 $f$ is separable then there is a
$f$ is separable then there is a  ${\it\sigma}$-localization
${\it\sigma}$-localization  $X^{\prime }$ of
$X^{\prime }$ of  $X$ and
$X$ and  $Y^{\prime }$ of
$Y^{\prime }$ of  $Y$ such that
$Y$ such that  $f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is
$f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is  ${\it\sigma}$-pro-smooth.
${\it\sigma}$-pro-smooth.(2) If
 $f$ is separable algebraic, then there is a
$f$ is separable algebraic, then there is a  ${\it\sigma}$-localization
${\it\sigma}$-localization  $X^{\prime }$ of
$X^{\prime }$ of  $X$ and
$X$ and  $Y^{\prime }$ of
$Y^{\prime }$ of  $Y$ such that
$Y$ such that  $f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is
$f\,\restriction\,X^{\prime }\cap f^{-1}(Y^{\prime })$ is  ${\it\sigma}$-pro-étale.
${\it\sigma}$-pro-étale.
Corollary 3.9. Let ![]() $(X,{\it\sigma})$ be a transformally integral separable difference scheme of finite
$(X,{\it\sigma})$ be a transformally integral separable difference scheme of finite ![]() ${\it\sigma}$-type over
${\it\sigma}$-type over ![]() $(R,{\it\sigma})$. There is a
$(R,{\it\sigma})$. There is a ![]() ${\it\sigma}$-localization
${\it\sigma}$-localization ![]() $X^{\prime }$ of
$X^{\prime }$ of ![]() $X$ and
$X$ and ![]() $R^{\prime }$ of
$R^{\prime }$ of ![]() $R$ such that
$R$ such that ![]() $X^{\prime }/R^{\prime }$ is normal (in the sense of 3.27).
$X^{\prime }/R^{\prime }$ is normal (in the sense of 3.27).
Proof. By 3.8, take a ![]() ${\it\sigma}$-localization
${\it\sigma}$-localization ![]() $X^{\prime }/R^{\prime }$ which is
$X^{\prime }/R^{\prime }$ which is ![]() ${\it\sigma}$-pro-smooth.◻
${\it\sigma}$-pro-smooth.◻
Definition 3.10. Given a difference-polynomial ring  $P=R[\bar{x}]_{{\rm\Sigma}}$ over
$P=R[\bar{x}]_{{\rm\Sigma}}$ over ![]() $(R,{\it\varsigma})$, let us write
$(R,{\it\varsigma})$, let us write  $P_{i}=R[\bar{x},{\rm\Sigma}\bar{x},\ldots ,{\rm\Sigma}^{i}\bar{x}]\subseteq P$. We shall say that an
$P_{i}=R[\bar{x},{\rm\Sigma}\bar{x},\ldots ,{\rm\Sigma}^{i}\bar{x}]\subseteq P$. We shall say that an ![]() $(R,{\it\varsigma})$-algebra
$(R,{\it\varsigma})$-algebra ![]() $(A,{\rm\Sigma})$ of finite
$(A,{\rm\Sigma})$ of finite ![]() ${\rm\Sigma}$-type is directly presented if there exists an
${\rm\Sigma}$-type is directly presented if there exists an ![]() $(R,{\it\varsigma})$-epimorphism from some
$(R,{\it\varsigma})$-epimorphism from some ![]() ${\rm\Sigma}$-polynomial ring
${\rm\Sigma}$-polynomial ring 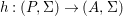 $h:(P,{\rm\Sigma})\rightarrow (A,{\rm\Sigma})$ whose kernel
$h:(P,{\rm\Sigma})\rightarrow (A,{\rm\Sigma})$ whose kernel ![]() $I$ is
$I$ is ![]() ${\rm\Sigma}$-generated by
${\rm\Sigma}$-generated by ![]() $I\cap P_{1}$.
$I\cap P_{1}$.
An affine difference scheme is directly presented over ![]() $(R,{\it\varsigma})$ if it is the spectrum of a directly presented
$(R,{\it\varsigma})$ if it is the spectrum of a directly presented ![]() $(R,{\it\varsigma})$-algebra.
$(R,{\it\varsigma})$-algebra.
Remark 3.11. Let 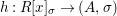 $h:R[x]_{{\it\sigma}}\rightarrow (A,{\it\sigma})$ be a direct presentation of
$h:R[x]_{{\it\sigma}}\rightarrow (A,{\it\sigma})$ be a direct presentation of ![]() $(A,{\it\sigma})$ over
$(A,{\it\sigma})$ over ![]() $(R,{\it\varsigma})$. Let
$(R,{\it\varsigma})$. Let 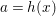 $a=h(x)$ be an associated choice of
$a=h(x)$ be an associated choice of ![]() ${\it\sigma}$-generators of
${\it\sigma}$-generators of ![]() $A$, and let
$A$, and let ![]() $A_{n}$ be the projective system of Zariski closures constructed above. Then clearly
$A_{n}$ be the projective system of Zariski closures constructed above. Then clearly ![]() $(A,{\it\sigma})$ can be reconstructed from the morphisms
$(A,{\it\sigma})$ can be reconstructed from the morphisms  $A_{0}{\hookrightarrow}A_{1}\stackrel{{\it\sigma}}{\leftarrow }A_{0}$. Similarly,
$A_{0}{\hookrightarrow}A_{1}\stackrel{{\it\sigma}}{\leftarrow }A_{0}$. Similarly, 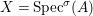 $X=\text{Spec}^{{\it\sigma}}(A)$ is “presented” by the algebraic correspondence
$X=\text{Spec}^{{\it\sigma}}(A)$ is “presented” by the algebraic correspondence 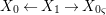 $X_{0}\leftarrow X_{1}\rightarrow X_{0{\it\varsigma}}$ over
$X_{0}\leftarrow X_{1}\rightarrow X_{0{\it\varsigma}}$ over ![]() $R$. Conversely, for every closed immersion
$R$. Conversely, for every closed immersion 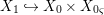 $X_{1}{\hookrightarrow}X_{0}\times X_{0{\it\varsigma}}$ of
$X_{1}{\hookrightarrow}X_{0}\times X_{0{\it\varsigma}}$ of ![]() $R$-schemes
$R$-schemes ![]() $X_{0}$,
$X_{0}$, ![]() $X_{1}$, Hrushovski [Reference Hrushovski18] gives a construction of the associated directly presented difference scheme.
$X_{1}$, Hrushovski [Reference Hrushovski18] gives a construction of the associated directly presented difference scheme.
In [Reference Tomašić23], we consider directly presented difference schemes ![]() $(X,{\rm\Sigma})$ associated with a collection of algebraic correspondences
$(X,{\rm\Sigma})$ associated with a collection of algebraic correspondences 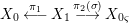 $X_{0}\stackrel{{\it\pi}_{1}}{\longleftarrow }X_{1}\stackrel{{\it\pi}_{2}({\it\sigma})}{\longrightarrow }X_{0{\it\varsigma}}$, for
$X_{0}\stackrel{{\it\pi}_{1}}{\longleftarrow }X_{1}\stackrel{{\it\pi}_{2}({\it\sigma})}{\longrightarrow }X_{0{\it\varsigma}}$, for ![]() ${\it\sigma}\in {\rm\Sigma}$.
${\it\sigma}\in {\rm\Sigma}$.
Definition 3.12. Let ![]() $(X,{\rm\Sigma})$ be a directly presented difference scheme over
$(X,{\rm\Sigma})$ be a directly presented difference scheme over ![]() $(R,{\it\varsigma})$ associated with algebraic correspondences
$(R,{\it\varsigma})$ associated with algebraic correspondences 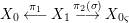 $X_{0}\stackrel{{\it\pi}_{1}}{\longleftarrow }X_{1}\stackrel{{\it\pi}_{2}({\it\sigma})}{\longrightarrow }X_{0{\it\varsigma}}$, for
$X_{0}\stackrel{{\it\pi}_{1}}{\longleftarrow }X_{1}\stackrel{{\it\pi}_{2}({\it\sigma})}{\longrightarrow }X_{0{\it\varsigma}}$, for ![]() ${\it\sigma}\in {\rm\Sigma}$, and let
${\it\sigma}\in {\rm\Sigma}$, and let ![]() $P$ be a property of
$P$ be a property of ![]() $R$-algebraic schemes. We say that
$R$-algebraic schemes. We say that ![]() $X$ is directly
$X$ is directly ![]() $P$, if
$P$, if ![]() $X_{0}$,
$X_{0}$, ![]() $X_{1}$ and
$X_{1}$ and ![]() $X_{0{\it\varsigma}}$ have the property
$X_{0{\it\varsigma}}$ have the property ![]() $P$.
$P$.
Definition 3.13. With notation of 3.12, a difference scheme ![]() $(X,{\rm\Sigma})$ is said to be directly geometrically transformally integral if it is directly geometrically integral and
$(X,{\rm\Sigma})$ is said to be directly geometrically transformally integral if it is directly geometrically integral and ![]() ${\it\pi}_{1}$,
${\it\pi}_{1}$, ![]() ${\it\pi}_{2}({\it\sigma})$ are dominant, for all
${\it\pi}_{2}({\it\sigma})$ are dominant, for all ![]() ${\it\sigma}\in {\rm\Sigma}$.
${\it\sigma}\in {\rm\Sigma}$.
Lemma 3.14. Let 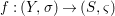 $f:(Y,{\it\sigma})\rightarrow (S,{\it\varsigma})$ be a morphism of finite
$f:(Y,{\it\sigma})\rightarrow (S,{\it\varsigma})$ be a morphism of finite ![]() ${\it\sigma}$-type of transformally integral difference schemes whose generic fiber is geometrically transformally integral. Then there is a
${\it\sigma}$-type of transformally integral difference schemes whose generic fiber is geometrically transformally integral. Then there is a ![]() ${\it\sigma}$-localization
${\it\sigma}$-localization ![]() $Y^{\prime }$ of
$Y^{\prime }$ of ![]() $Y$,
$Y$, ![]() $Y^{\prime }$ of
$Y^{\prime }$ of ![]() $Y$ such that
$Y$ such that 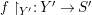 $f\restriction_{Y^{\prime }}:Y^{\prime }\rightarrow S^{\prime }$ has directly geometrically transformally integral fibers.
$f\restriction_{Y^{\prime }}:Y^{\prime }\rightarrow S^{\prime }$ has directly geometrically transformally integral fibers.
Proof. The Preparation Lemma 3.3 shows that, modulo a localization, ![]() $Y$ can be made directly presented over
$Y$ can be made directly presented over ![]() $S$. Writing
$S$. Writing ![]() ${\it\eta}$ for the generic point of
${\it\eta}$ for the generic point of ![]() $S$,
$S$, ![]() $Y_{{\it\eta}}$ is assumed to be geometrically transformally integral, so
$Y_{{\it\eta}}$ is assumed to be geometrically transformally integral, so ![]() $Y_{0,{\it\eta}}$,
$Y_{0,{\it\eta}}$, ![]() $Y_{1,{\it\eta}}$ and
$Y_{1,{\it\eta}}$ and  $Y_{0{\it\varsigma},{\it\eta}}=Y_{0,{\it\varsigma}{\it\eta}}$ are geometrically integral and the relevant projections are all dominant. Using the constructibility of the property of being geometrically integral [1, Tag 055G], as well as the dominance of a morphism, we can
$Y_{0{\it\varsigma},{\it\eta}}=Y_{0,{\it\varsigma}{\it\eta}}$ are geometrically integral and the relevant projections are all dominant. Using the constructibility of the property of being geometrically integral [1, Tag 055G], as well as the dominance of a morphism, we can ![]() ${\it\varsigma}$-localize
${\it\varsigma}$-localize ![]() $S$ to obtain that every fiber
$S$ to obtain that every fiber ![]() $Y_{s}$ is directly transformally integral. ◻
$Y_{s}$ is directly transformally integral. ◻
Lemma 3.15. Let 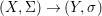 $(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ be an étale Galois cover of transformally integral difference schemes of finite transformal type over
$(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ be an étale Galois cover of transformally integral difference schemes of finite transformal type over ![]() $(S,{\it\varsigma})$ such that the generic fibers of
$(S,{\it\varsigma})$ such that the generic fibers of ![]() $X$ and
$X$ and ![]() $Y$ over
$Y$ over ![]() $S$ are geometrically transformally integral. Then there exist localizations
$S$ are geometrically transformally integral. Then there exist localizations ![]() $X^{\prime }$ of
$X^{\prime }$ of ![]() $X$,
$X$, ![]() $Y^{\prime }$ of
$Y^{\prime }$ of ![]() $Y$ and
$Y$ and ![]() $S^{\prime }$ of
$S^{\prime }$ of ![]() $S$ such that for every
$S$ such that for every ![]() $s\in S^{\prime }$, the fibers
$s\in S^{\prime }$, the fibers ![]() $X_{s}^{\prime }$ and
$X_{s}^{\prime }$ and ![]() $Y_{s}^{\prime }$ are directly geometrically transformally integral and
$Y_{s}^{\prime }$ are directly geometrically transformally integral and
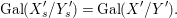 $$\begin{eqnarray}\text{Gal}(X_{s}^{\prime }/Y_{s}^{\prime })=\text{Gal}(X^{\prime }/Y^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\text{Gal}(X_{s}^{\prime }/Y_{s}^{\prime })=\text{Gal}(X^{\prime }/Y^{\prime }).\end{eqnarray}$$Proof. It is an exercise in dealing with constructible properties of algebraic schemes and correspondences to find an ad hoc proof of this claim. We offer a more conceptual proof, referring to the techniques of [Reference Tomašić23]. By a localization, we may assume that ![]() $X\rightarrow Y$ is a direct Galois cover whose direct Galois group equals
$X\rightarrow Y$ is a direct Galois cover whose direct Galois group equals  $\text{Gal}(X/Y)$. Using the assumption on the generic fibers, by a further localization and 3.14 we can achieve that the fibers
$\text{Gal}(X/Y)$. Using the assumption on the generic fibers, by a further localization and 3.14 we can achieve that the fibers ![]() $X_{s}$ and
$X_{s}$ and ![]() $Y_{s}$ are directly geometrically transformally integral and then the direct Galois groups of
$Y_{s}$ are directly geometrically transformally integral and then the direct Galois groups of ![]() $X_{s}/Y_{s}$ and
$X_{s}/Y_{s}$ and ![]() $X/S$ obviously coincide. By the construction, the direct Galois groups are in fact Galois groups and we are done.◻
$X/S$ obviously coincide. By the construction, the direct Galois groups are in fact Galois groups and we are done.◻
3.2 Local properties
This subsection is mostly concerned with the question of whether it is reasonable to expect that if a property holds locally, at every point of a fixed-point spectrum of a difference ring, then it also holds globally.
Definition 3.16. Let ![]() $(M,{\it\sigma})$ be an
$(M,{\it\sigma})$ be an ![]() $(A,{\it\sigma})$-module and let
$(A,{\it\sigma})$-module and let ![]() $(N,{\it\sigma})$ be a submodule.
$(N,{\it\sigma})$ be a submodule.
(1) We say that
 $(M,{\it\sigma})$ is well-mixed if
$(M,{\it\sigma})$ is well-mixed if  $am=0$ implies
$am=0$ implies  ${\it\sigma}(a)m=0$ for all
${\it\sigma}(a)m=0$ for all  $a\in A$,
$a\in A$,  $m\in M$.
$m\in M$.(2) We say that
 $(N,{\it\sigma})$ is a well-mixed submodule of
$(N,{\it\sigma})$ is a well-mixed submodule of  $(M,{\it\sigma})$ if the module
$(M,{\it\sigma})$ if the module  $M/N$ is well-mixed.
$M/N$ is well-mixed.
Clearly ![]() $(M,{\it\sigma})$ is well-mixed if and only if the annihilator
$(M,{\it\sigma})$ is well-mixed if and only if the annihilator  $\text{Ann}(m)$ of any
$\text{Ann}(m)$ of any ![]() $m\in M$ is a well-mixed
$m\in M$ is a well-mixed ![]() ${\it\sigma}$-ideal in
${\it\sigma}$-ideal in ![]() $(A,{\it\sigma})$. Indeed, if
$(A,{\it\sigma})$. Indeed, if 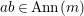 $ab\in \text{Ann}(m)$, then
$ab\in \text{Ann}(m)$, then 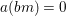 $a(bm)=0$ so
$a(bm)=0$ so 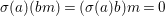 ${\it\sigma}(a)(bm)=({\it\sigma}(a)b)m=0$ and
${\it\sigma}(a)(bm)=({\it\sigma}(a)b)m=0$ and 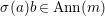 ${\it\sigma}(a)b\in \text{Ann}(m)$.
${\it\sigma}(a)b\in \text{Ann}(m)$.
Moreover, since the intersection of well-mixed submodules is well-mixed and ![]() $M$ is trivially a well-mixed submodule of itself, for every submodule
$M$ is trivially a well-mixed submodule of itself, for every submodule ![]() $(N,{\it\sigma})$ of
$(N,{\it\sigma})$ of ![]() $(M,{\it\sigma})$ there exists a smallest well-mixed submodule
$(M,{\it\sigma})$ there exists a smallest well-mixed submodule ![]() $[N]_{w}$ containing
$[N]_{w}$ containing ![]() $N$. Thus
$N$. Thus ![]() $[0]_{w}$ is the smallest well-mixed submodule of
$[0]_{w}$ is the smallest well-mixed submodule of ![]() $(M,{\it\sigma})$ associated with the largest well-mixed quotient
$(M,{\it\sigma})$ associated with the largest well-mixed quotient ![]() $M_{w}$ of
$M_{w}$ of ![]() $M$.
$M$.
Proposition 3.17. Let ![]() $(M,{\it\sigma})$ be a well-mixed
$(M,{\it\sigma})$ be a well-mixed ![]() $(A,{\it\sigma})$-module. The following are equivalent.
$(A,{\it\sigma})$-module. The following are equivalent.
(1)
 $M=0$;
$M=0$;(2)
 $M_{\mathfrak{p}}=0$ for every
$M_{\mathfrak{p}}=0$ for every  $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$;
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$;(3)
 $M_{\mathfrak{p}}=0$ for every
$M_{\mathfrak{p}}=0$ for every  $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in  $\text{Spec}^{{\it\sigma}}(A)$.
$\text{Spec}^{{\it\sigma}}(A)$.
Proof. It is clear that (1) implies (2) and (2) implies (3). Suppose that (3) holds but ![]() $M\neq 0$. Let
$M\neq 0$. Let 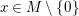 $x\in M\setminus \{0\}$ and let
$x\in M\setminus \{0\}$ and let 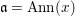 $\mathfrak{a}=\text{Ann}(x)$. Then
$\mathfrak{a}=\text{Ann}(x)$. Then ![]() $\mathfrak{a}\neq (1)$ is well-mixed and, by [Reference Tomašić24, 2.21],
$\mathfrak{a}\neq (1)$ is well-mixed and, by [Reference Tomašić24, 2.21], 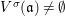 $V^{{\it\sigma}}(\mathfrak{a})\neq \emptyset$. Choose a maximal
$V^{{\it\sigma}}(\mathfrak{a})\neq \emptyset$. Choose a maximal ![]() $\mathfrak{p}$ in
$\mathfrak{p}$ in ![]() $V^{{\it\sigma}}(\mathfrak{a})$. Since
$V^{{\it\sigma}}(\mathfrak{a})$. Since ![]() $x/1=0$ in
$x/1=0$ in ![]() $M_{\mathfrak{p}}$, there exists an
$M_{\mathfrak{p}}$, there exists an ![]() $a\notin \mathfrak{p}$ such that
$a\notin \mathfrak{p}$ such that ![]() $ax=0$, which is in contradiction with
$ax=0$, which is in contradiction with 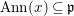 $\text{Ann}(x)\subseteq \mathfrak{p}$.◻
$\text{Ann}(x)\subseteq \mathfrak{p}$.◻
Corollary 3.18. Let ![]() $(M,{\it\sigma})$ be an
$(M,{\it\sigma})$ be an ![]() $(A,{\it\sigma})$-module. If
$(A,{\it\sigma})$-module. If ![]() $M_{\mathfrak{p}}=0$ for every
$M_{\mathfrak{p}}=0$ for every 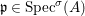 $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$, then
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$, then  $M_{w}=0$.
$M_{w}=0$.
The above can be sharpened as follows.
Proposition 3.19. Let ![]() $(M,{\it\sigma})$ be an
$(M,{\it\sigma})$ be an ![]() $(A,{\it\sigma})$-module. If
$(A,{\it\sigma})$-module. If  $(M_{\mathfrak{p}})_{w}=0$ for every
$(M_{\mathfrak{p}})_{w}=0$ for every ![]() $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in 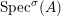 $\text{Spec}^{{\it\sigma}}(A)$, then
$\text{Spec}^{{\it\sigma}}(A)$, then  $M_{w}=0$.
$M_{w}=0$.
Proof. Using the universal properties of localization and passing to well-mixed quotients, as well as the fact that localization is an exact functor, we construct a commutative diagram
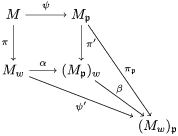
in which ![]() ${\it\pi}$ and
${\it\pi}$ and ![]() ${\it\pi}^{\prime }$ are surjective, so we conclude that
${\it\pi}^{\prime }$ are surjective, so we conclude that ![]() ${\it\pi}_{\mathfrak{p}}$ and
${\it\pi}_{\mathfrak{p}}$ and ![]() ${\it\beta}$ are also surjective. Therefore,
${\it\beta}$ are also surjective. Therefore,  $(M_{\mathfrak{p}})_{w}=0$ implies that
$(M_{\mathfrak{p}})_{w}=0$ implies that  $(M_{w})_{\mathfrak{p}}=0$ and we finish by 3.17.◻
$(M_{w})_{\mathfrak{p}}=0$ and we finish by 3.17.◻
Proposition 3.20. Let 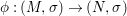 ${\it\phi}:(M,{\it\sigma})\rightarrow (N,{\it\sigma})$ be an
${\it\phi}:(M,{\it\sigma})\rightarrow (N,{\it\sigma})$ be an ![]() $(A,{\it\sigma})$-module homomorphism and assume that
$(A,{\it\sigma})$-module homomorphism and assume that ![]() $(M,{\it\sigma})$ is well-mixed. The following are equivalent.
$(M,{\it\sigma})$ is well-mixed. The following are equivalent.
(1)
 ${\it\phi}$ is injective;
${\it\phi}$ is injective;(2)
 ${\it\phi}_{\mathfrak{p}}:M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is injective for every
${\it\phi}_{\mathfrak{p}}:M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is injective for every  $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$;
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$;(3)
 ${\it\phi}_{\mathfrak{p}}:M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is injective for every
${\it\phi}_{\mathfrak{p}}:M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is injective for every  $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in  $\text{Spec}^{{\it\sigma}}(A)$.
$\text{Spec}^{{\it\sigma}}(A)$.
Proof. (1) ![]() $\Rightarrow$ (2). If
$\Rightarrow$ (2). If 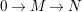 $0\rightarrow M\rightarrow N$ is exact, since localization is exact, we get that
$0\rightarrow M\rightarrow N$ is exact, since localization is exact, we get that  $0\rightarrow M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is also exact. (2)
$0\rightarrow M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is also exact. (2) ![]() $\Rightarrow$ (3) is trivial.
$\Rightarrow$ (3) is trivial.
(3) ![]() $\Rightarrow$ (1). Let
$\Rightarrow$ (1). Let  $M^{\prime }=\ker {\it\phi}$. Then
$M^{\prime }=\ker {\it\phi}$. Then 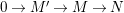 $0\rightarrow M^{\prime }\rightarrow M\rightarrow N$ is exact so
$0\rightarrow M^{\prime }\rightarrow M\rightarrow N$ is exact so 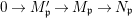 $0\rightarrow M_{\mathfrak{p}}^{\prime }\rightarrow M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is exact for every
$0\rightarrow M_{\mathfrak{p}}^{\prime }\rightarrow M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is exact for every 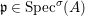 $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. By assumption,
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. By assumption, ![]() $M_{\mathfrak{p}}^{\prime }=0$ for every
$M_{\mathfrak{p}}^{\prime }=0$ for every 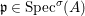 $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. Since
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. Since ![]() $M^{\prime }$ is well-mixed (as a submodule of
$M^{\prime }$ is well-mixed (as a submodule of ![]() $M$), by 3.17 we conclude that
$M$), by 3.17 we conclude that ![]() $M^{\prime }=0$.◻
$M^{\prime }=0$.◻
We shall say that an ![]() $(A,{\it\sigma})$-module homomorphism
$(A,{\it\sigma})$-module homomorphism 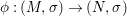 ${\it\phi}:(M,{\it\sigma})\rightarrow (N,{\it\sigma})$ is almost surjective, if
${\it\phi}:(M,{\it\sigma})\rightarrow (N,{\it\sigma})$ is almost surjective, if  $[\text{im}({\it\phi})]_{w}=N$ (or, equivalently, if
$[\text{im}({\it\phi})]_{w}=N$ (or, equivalently, if  $\text{coker}({\it\phi})_{w}=0$).
$\text{coker}({\it\phi})_{w}=0$).
Proposition 3.21. Let 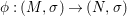 ${\it\phi}:(M,{\it\sigma})\rightarrow (N,{\it\sigma})$ be an
${\it\phi}:(M,{\it\sigma})\rightarrow (N,{\it\sigma})$ be an ![]() $(A,{\it\sigma})$-module homomorphism. If
$(A,{\it\sigma})$-module homomorphism. If 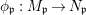 ${\it\phi}_{\mathfrak{p}}:M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is almost surjective for every
${\it\phi}_{\mathfrak{p}}:M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}$ is almost surjective for every ![]() $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in 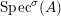 $\text{Spec}^{{\it\sigma}}(A)$, then
$\text{Spec}^{{\it\sigma}}(A)$, then ![]() ${\it\phi}$ is almost surjective.
${\it\phi}$ is almost surjective.
Proof. Let  $N^{\prime }=\text{coker}({\it\phi})$. Then
$N^{\prime }=\text{coker}({\it\phi})$. Then  $M\rightarrow N\rightarrow N^{\prime }\rightarrow 0$ is exact, and by localization
$M\rightarrow N\rightarrow N^{\prime }\rightarrow 0$ is exact, and by localization 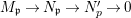 $M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}\rightarrow N_{p}^{\prime }\rightarrow 0$ is exact for every
$M_{\mathfrak{p}}\rightarrow N_{\mathfrak{p}}\rightarrow N_{p}^{\prime }\rightarrow 0$ is exact for every 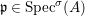 $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. By assumption,
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. By assumption, 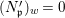 $(N_{\mathfrak{p}}^{\prime })_{w}=0$ for all
$(N_{\mathfrak{p}}^{\prime })_{w}=0$ for all ![]() $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in 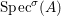 $\text{Spec}^{{\it\sigma}}(A)$ and 3.19 implies that
$\text{Spec}^{{\it\sigma}}(A)$ and 3.19 implies that ![]() $N_{w}^{\prime }=0$.◻
$N_{w}^{\prime }=0$.◻
Lemma 3.22. [Reference Eisenbud10, 6.4]
Let ![]() $M$ and
$M$ and ![]() $N$ be
$N$ be ![]() $A$-modules and suppose
$A$-modules and suppose ![]() $N$ is generated by
$N$ is generated by ![]() $\{n_{i}\}$. Then every element of
$\{n_{i}\}$. Then every element of 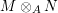 $M\otimes _{A}N$ can be written as
$M\otimes _{A}N$ can be written as 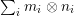 $\sum _{i}m_{i}\otimes n_{i}$ with finitely many nonzero
$\sum _{i}m_{i}\otimes n_{i}$ with finitely many nonzero ![]() $m_{i}$ and
$m_{i}$ and 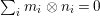 $\sum _{i}m_{i}\otimes n_{i}=0$ in
$\sum _{i}m_{i}\otimes n_{i}=0$ in 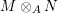 $M\otimes _{A}N$ if and only if there exist
$M\otimes _{A}N$ if and only if there exist 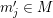 $m_{j}^{\prime }\in M$ and
$m_{j}^{\prime }\in M$ and ![]() $a_{ij}\in A$ such that for every
$a_{ij}\in A$ such that for every ![]() $i$,
$i$,
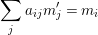 $$\begin{eqnarray}\mathop{\sum }_{j}a_{ij}m_{j}^{\prime }=m_{i}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j}a_{ij}m_{j}^{\prime }=m_{i}\end{eqnarray}$$ and for every ![]() $j$,
$j$,
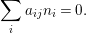 $$\begin{eqnarray}\mathop{\sum }_{i}a_{ij}n_{i}=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i}a_{ij}n_{i}=0.\end{eqnarray}$$Proposition 3.23. Let ![]() $(M,{\it\sigma})$ and
$(M,{\it\sigma})$ and ![]() $(N,{\it\sigma})$ be
$(N,{\it\sigma})$ be ![]() $(A,{\it\sigma})$-modules with
$(A,{\it\sigma})$-modules with ![]() $(N,{\it\sigma})$ well-mixed. Then
$(N,{\it\sigma})$ well-mixed. Then  $(M,{\it\sigma})\otimes _{(A,{\it\sigma})}(N,{\it\sigma})$ is well-mixed.
$(M,{\it\sigma})\otimes _{(A,{\it\sigma})}(N,{\it\sigma})$ is well-mixed.
Proof. Pick a set of generators ![]() $\{n_{i}\}$ for
$\{n_{i}\}$ for ![]() $N$. Suppose
$N$. Suppose 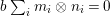 $b\sum _{i}m_{i}\otimes n_{i}=0$. Then
$b\sum _{i}m_{i}\otimes n_{i}=0$. Then 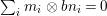 $\sum _{i}m_{i}\otimes bn_{i}=0$ so 3.22 implies the existence of
$\sum _{i}m_{i}\otimes bn_{i}=0$ so 3.22 implies the existence of 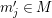 $m_{j}^{\prime }\in M$ and
$m_{j}^{\prime }\in M$ and ![]() $a_{ij}\in A$ such that for every
$a_{ij}\in A$ such that for every ![]() $i$,
$i$, 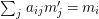 $\sum _{j}a_{ij}m_{j}^{\prime }=m_{i}$ and for every
$\sum _{j}a_{ij}m_{j}^{\prime }=m_{i}$ and for every ![]() $j$,
$j$, 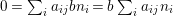 $0=\sum _{i}a_{ij}bn_{i}=b\sum _{i}a_{ij}n_{i}$. Since the latter holds in
$0=\sum _{i}a_{ij}bn_{i}=b\sum _{i}a_{ij}n_{i}$. Since the latter holds in ![]() $(N,{\it\sigma})$ which is well-mixed, we get that
$(N,{\it\sigma})$ which is well-mixed, we get that 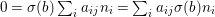 $0={\it\sigma}(b)\sum _{i}a_{ij}n_{i}=\sum _{i}a_{ij}{\it\sigma}(b)n_{i}$. Using 3.22 again, it follows that
$0={\it\sigma}(b)\sum _{i}a_{ij}n_{i}=\sum _{i}a_{ij}{\it\sigma}(b)n_{i}$. Using 3.22 again, it follows that 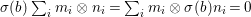 ${\it\sigma}(b)\sum _{i}m_{i}\otimes n_{i}=\sum _{i}m_{i}\otimes {\it\sigma}(b)n_{i}=0$.◻
${\it\sigma}(b)\sum _{i}m_{i}\otimes n_{i}=\sum _{i}m_{i}\otimes {\it\sigma}(b)n_{i}=0$.◻
Proposition 3.24. Let ![]() $(M,{\it\sigma})$ be a well-mixed
$(M,{\it\sigma})$ be a well-mixed ![]() $(A,{\it\sigma})$-module. The following are equivalent.
$(A,{\it\sigma})$-module. The following are equivalent.
(1)
 $M$ is a flat
$M$ is a flat  $A$-module.
$A$-module.(2)
 $M_{\mathfrak{p}}$ is a flat
$M_{\mathfrak{p}}$ is a flat  $A_{\mathfrak{p}}$-module for every
$A_{\mathfrak{p}}$-module for every  $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$.
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$.(3)
 $M_{\mathfrak{p}}$ is a flat
$M_{\mathfrak{p}}$ is a flat  $A_{\mathfrak{p}}$-module for every
$A_{\mathfrak{p}}$-module for every  $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in  $\text{Spec}^{{\it\sigma}}(A)$.
$\text{Spec}^{{\it\sigma}}(A)$.
Proof. (1) ![]() $\Rightarrow$ (2). Assuming
$\Rightarrow$ (2). Assuming ![]() $(i)$, it is classically known that
$(i)$, it is classically known that ![]() $M_{\mathfrak{p}}$ is a flat
$M_{\mathfrak{p}}$ is a flat ![]() $A_{\mathfrak{p}}$ module for every prime
$A_{\mathfrak{p}}$ module for every prime ![]() $\mathfrak{p}$. (2)
$\mathfrak{p}$. (2) ![]() $\Rightarrow$ (3) is trivial.
$\Rightarrow$ (3) is trivial.
(3) ![]() $\Rightarrow$ (1). Let
$\Rightarrow$ (1). Let 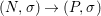 $(N,{\it\sigma})\rightarrow (P,{\it\sigma})$ be injective. Then
$(N,{\it\sigma})\rightarrow (P,{\it\sigma})$ be injective. Then 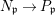 $N_{\mathfrak{p}}\rightarrow P_{\mathfrak{p}}$ is injective for every
$N_{\mathfrak{p}}\rightarrow P_{\mathfrak{p}}$ is injective for every 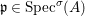 $\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. By assumption,
$\mathfrak{p}\in \text{Spec}^{{\it\sigma}}(A)$. By assumption,  $N_{\mathfrak{p}}\otimes _{A_{\mathfrak{p}}}M_{\mathfrak{p}}\rightarrow P_{\mathfrak{p}}\otimes _{A_{\mathfrak{p}}}M_{\mathfrak{p}}$ is injective and thus
$N_{\mathfrak{p}}\otimes _{A_{\mathfrak{p}}}M_{\mathfrak{p}}\rightarrow P_{\mathfrak{p}}\otimes _{A_{\mathfrak{p}}}M_{\mathfrak{p}}$ is injective and thus  $\left(N\otimes _{A}M\right)_{\mathfrak{p}}\rightarrow \left(P\otimes _{A}M\right)_{\mathfrak{p}}$ is injective for all
$\left(N\otimes _{A}M\right)_{\mathfrak{p}}\rightarrow \left(P\otimes _{A}M\right)_{\mathfrak{p}}$ is injective for all ![]() $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in 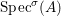 $\text{Spec}^{{\it\sigma}}(A)$. Since
$\text{Spec}^{{\it\sigma}}(A)$. Since  $N\otimes _{A}M$ is well-mixed by 3.23, Proposition 3.20 implies that
$N\otimes _{A}M$ is well-mixed by 3.23, Proposition 3.20 implies that  $N\otimes _{A}M\rightarrow P\otimes _{A}M$ is injective.◻
$N\otimes _{A}M\rightarrow P\otimes _{A}M$ is injective.◻
Remark 3.25. Let  $(A,{\it\sigma})\rightarrow (B,{\it\sigma})$ be a homomorphism of well-mixed difference rings such that
$(A,{\it\sigma})\rightarrow (B,{\it\sigma})$ be a homomorphism of well-mixed difference rings such that ![]() $B$ is a flat
$B$ is a flat ![]() $A$-module and denote by
$A$-module and denote by ![]() $\bar{A}$ and
$\bar{A}$ and ![]() $\bar{B}$ the rings of global sections of
$\bar{B}$ the rings of global sections of 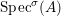 $\text{Spec}^{{\it\sigma}}(A)$ and
$\text{Spec}^{{\it\sigma}}(A)$ and 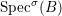 $\text{Spec}^{{\it\sigma}}(B)$. We can consider
$\text{Spec}^{{\it\sigma}}(B)$. We can consider ![]() $\bar{B}$ as an
$\bar{B}$ as an ![]() $A$-module via the morphism
$A$-module via the morphism 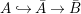 $A{\hookrightarrow}\bar{A}\rightarrow \bar{B}$ as in 2.8, and we can conclude that
$A{\hookrightarrow}\bar{A}\rightarrow \bar{B}$ as in 2.8, and we can conclude that ![]() $\bar{B}$ is flat over
$\bar{B}$ is flat over ![]() $A$. Indeed,
$A$. Indeed, ![]() $\bar{B}$ is well-mixed, and we know that
$\bar{B}$ is well-mixed, and we know that 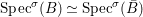 $\text{Spec}^{{\it\sigma}}(B)\simeq \text{Spec}^{{\it\sigma}}(\bar{B})$ and
$\text{Spec}^{{\it\sigma}}(B)\simeq \text{Spec}^{{\it\sigma}}(\bar{B})$ and 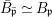 $\bar{B}_{\bar{\mathfrak{p}}}\simeq B_{\mathfrak{p}}$, which suffices to apply 3.24.
$\bar{B}_{\bar{\mathfrak{p}}}\simeq B_{\mathfrak{p}}$, which suffices to apply 3.24.
Proposition 3.26. Let ![]() $(A,{\it\sigma})$ be a transformal domain. If
$(A,{\it\sigma})$ be a transformal domain. If ![]() $A_{\mathfrak{p}}$ is normal for every
$A_{\mathfrak{p}}$ is normal for every ![]() $\mathfrak{p}$ maximal in
$\mathfrak{p}$ maximal in 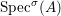 $\text{Spec}^{{\it\sigma}}(A)$, then
$\text{Spec}^{{\it\sigma}}(A)$, then ![]() $A$ is almost normal in the sense that there is a normal transformal domain
$A$ is almost normal in the sense that there is a normal transformal domain ![]() $C$ with
$C$ with 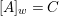 $[A]_{w}=C$.
$[A]_{w}=C$.
Proof. Let ![]() $K$ be the fraction field of
$K$ be the fraction field of ![]() $A$, let
$A$, let ![]() $C$ be the integral closure of
$C$ be the integral closure of ![]() $A$ in
$A$ in ![]() $K$ and denote by
$K$ and denote by 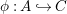 ${\it\phi}:A{\hookrightarrow}C$ the inclusion. By assumption, each
${\it\phi}:A{\hookrightarrow}C$ the inclusion. By assumption, each ![]() ${\it\phi}_{\mathfrak{p}}$ is surjective, so 3.21 implies that
${\it\phi}_{\mathfrak{p}}$ is surjective, so 3.21 implies that ![]() ${\it\phi}$ is almost surjective and thus
${\it\phi}$ is almost surjective and thus 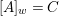 $[A]_{w}=C$.◻
$[A]_{w}=C$.◻
Definition 3.27. A difference scheme ![]() $(X,{\rm\Sigma})$ is said to be normal if every local ring
$(X,{\rm\Sigma})$ is said to be normal if every local ring ![]() ${\mathcal{O}}_{x}$, for
${\mathcal{O}}_{x}$, for ![]() $x\in X$, is normal.
$x\in X$, is normal.
3.3 Étale morphisms of difference schemes
Definition 3.28. A morphism 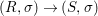 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally smooth (resp. formally unramified, formally étale), if for every solid commutative diagram
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally smooth (resp. formally unramified, formally étale), if for every solid commutative diagram
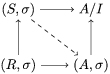
with ![]() $I$ a difference ideal satisfying
$I$ a difference ideal satisfying ![]() $I^{2}=0$, there exists at least one (resp. at most one, exactly one) dashed arrow making the diagram commutative.
$I^{2}=0$, there exists at least one (resp. at most one, exactly one) dashed arrow making the diagram commutative.
Recall that a morphism of rings ![]() $R\rightarrow S$ is defined to be formally smooth, formally unramified or formally étale by using exactly the same universal property in the category of commutative rings, omitting the difference structure.
$R\rightarrow S$ is defined to be formally smooth, formally unramified or formally étale by using exactly the same universal property in the category of commutative rings, omitting the difference structure.
Lemma 3.29. If 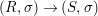 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally smooth, then
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally smooth, then ![]() $R\rightarrow S$ is formally smooth.
$R\rightarrow S$ is formally smooth.
Proof. Let 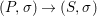 $(P,{\it\sigma})\rightarrow (S,{\it\sigma})$ be a surjective
$(P,{\it\sigma})\rightarrow (S,{\it\sigma})$ be a surjective ![]() $(R,{\it\sigma})$-algebra morphism from a difference-polynomial ring
$(R,{\it\sigma})$-algebra morphism from a difference-polynomial ring ![]() $P$, and let
$P$, and let ![]() $J$ be the kernel, which is a difference ideal. Consider the above diagram for
$J$ be the kernel, which is a difference ideal. Consider the above diagram for  $A=P/J^{2}$ and
$A=P/J^{2}$ and ![]() $I$ generated by
$I$ generated by ![]() $J$. By formal smoothness, we obtain a (difference) morphism
$J$. By formal smoothness, we obtain a (difference) morphism  $S\rightarrow P/J^{2}$ which is a right inverse to the surjection
$S\rightarrow P/J^{2}$ which is a right inverse to the surjection  $P/J^{2}\rightarrow S$, and thus
$P/J^{2}\rightarrow S$, and thus ![]() $R\rightarrow S$ is formally smooth using [1, 00TL].◻
$R\rightarrow S$ is formally smooth using [1, 00TL].◻
Remark 3.30. For a difference ![]() $(R,{\it\sigma})$-algebra
$(R,{\it\sigma})$-algebra ![]() $(S,{\it\sigma})$, the module of relative differentials
$(S,{\it\sigma})$, the module of relative differentials ![]() ${\rm\Omega}_{S/R}$ naturally classifies
${\rm\Omega}_{S/R}$ naturally classifies ![]() $R$-derivations that commute with
$R$-derivations that commute with ![]() ${\it\sigma}$. Indeed, if we let
${\it\sigma}$. Indeed, if we let ![]() $J$ be the kernel of the multiplication map
$J$ be the kernel of the multiplication map 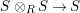 $S\otimes _{R}S\rightarrow S$, it is known that
$S\otimes _{R}S\rightarrow S$, it is known that 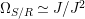 ${\rm\Omega}_{S/R}\simeq J/J^{2}$. However, in this context
${\rm\Omega}_{S/R}\simeq J/J^{2}$. However, in this context ![]() $J$ is a difference ideal and
$J$ is a difference ideal and ![]() $J/J^{2}$ comes equipped with a natural difference structure, which entails in particular that the universal
$J/J^{2}$ comes equipped with a natural difference structure, which entails in particular that the universal ![]() $R$-derivation
$R$-derivation 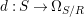 $d:S\rightarrow {\rm\Omega}_{S/R}$ satisfies
$d:S\rightarrow {\rm\Omega}_{S/R}$ satisfies
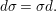 $$\begin{eqnarray}d{\it\sigma}={\it\sigma}d.\end{eqnarray}$$
$$\begin{eqnarray}d{\it\sigma}={\it\sigma}d.\end{eqnarray}$$Remark 3.31. The above is in contrast with the various notions of smoothness developed in Giabicani’s thesis [Reference Giabicani15]. With clear intent to apply his theory to the case where ![]() ${\it\sigma}$ is a power of the Frobenius automorphism, he postulates
${\it\sigma}$ is a power of the Frobenius automorphism, he postulates ![]() $d{\it\sigma}=0$. Another fundamental difference is that étale morphisms in our context as developed below are of relative total dimension
$d{\it\sigma}=0$. Another fundamental difference is that étale morphisms in our context as developed below are of relative total dimension ![]() $0$, whereas in Giabicani’s context they are of relative transformal dimension
$0$, whereas in Giabicani’s context they are of relative transformal dimension ![]() $0$.
$0$.
Remark 3.32. If ![]() $(B,{\it\sigma})$ is an
$(B,{\it\sigma})$ is an ![]() $(A,{\it\sigma})$-algebra of finite
$(A,{\it\sigma})$-algebra of finite ![]() ${\it\sigma}$-type, the second exact sequence for differentials implies that
${\it\sigma}$-type, the second exact sequence for differentials implies that ![]() ${\rm\Omega}_{B/A}$ is a finitely
${\rm\Omega}_{B/A}$ is a finitely ![]() ${\it\sigma}$-generated
${\it\sigma}$-generated ![]() $(B,{\it\sigma})$-module.
$(B,{\it\sigma})$-module.
Lemma 3.33. Given a difference morphism 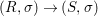 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$, the following statements are equivalent:
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$, the following statements are equivalent:
(1)
 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally unramified;
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally unramified;(2)
 $R\rightarrow S$ is formally unramified;
$R\rightarrow S$ is formally unramified;(3)
 ${\rm\Omega}_{S/R}=0$.
${\rm\Omega}_{S/R}=0$.
Proof. In view of 3.30, since 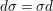 $d{\it\sigma}={\it\sigma}d$, the classical proof of the equivalence of (2) and (3) also works for the equivalence of (1) and (3).◻
$d{\it\sigma}={\it\sigma}d$, the classical proof of the equivalence of (2) and (3) also works for the equivalence of (1) and (3).◻
Corollary 3.34. Let 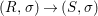 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ be a morphism. The following are equivalent:
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ be a morphism. The following are equivalent:
(1)
 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is almost formally unramified in the sense that
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is almost formally unramified in the sense that  $({\rm\Omega}_{S/R})_{w}=0$;
$({\rm\Omega}_{S/R})_{w}=0$;(2) for every
 $\mathfrak{q}\in \text{Spec}^{{\it\sigma}}(S)$ lying over
$\mathfrak{q}\in \text{Spec}^{{\it\sigma}}(S)$ lying over  $\mathfrak{p}=\mathfrak{q}\cap R$,
$\mathfrak{p}=\mathfrak{q}\cap R$,  $(R_{\mathfrak{p}},{\it\sigma})\rightarrow (S_{\mathfrak{q}},{\it\sigma})$ is formally unramified;
$(R_{\mathfrak{p}},{\it\sigma})\rightarrow (S_{\mathfrak{q}},{\it\sigma})$ is formally unramified;(3) for every
 $\mathfrak{q}\in \text{Spec}^{{\it\sigma}}(S)$ lying over
$\mathfrak{q}\in \text{Spec}^{{\it\sigma}}(S)$ lying over  $\mathfrak{p}=\mathfrak{q}\cap R$,
$\mathfrak{p}=\mathfrak{q}\cap R$,  $R_{\mathfrak{p}}\rightarrow S_{\mathfrak{q}}$ is formally unramified.
$R_{\mathfrak{p}}\rightarrow S_{\mathfrak{q}}$ is formally unramified.
Proof. Straightforward from 3.19 applied to the ![]() $(S,{\it\sigma})$-module
$(S,{\it\sigma})$-module ![]() ${\rm\Omega}_{S/R}$.◻
${\rm\Omega}_{S/R}$.◻
Corollary 3.35. A morphism 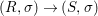 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally étale if and only if
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally étale if and only if ![]() $R\rightarrow S$ is formally étale.
$R\rightarrow S$ is formally étale.
Proof. If 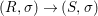 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally étale, it is both formally smooth and formally unramified. By 3.29,
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is formally étale, it is both formally smooth and formally unramified. By 3.29, ![]() $R\rightarrow S$ is formally smooth, and by 3.33, it is formally unramified, and therefore it is formally étale. The converse follows by a lengthy (although elementary) diagram chase, as noted in a discussion with M. Wibmer.◻
$R\rightarrow S$ is formally smooth, and by 3.33, it is formally unramified, and therefore it is formally étale. The converse follows by a lengthy (although elementary) diagram chase, as noted in a discussion with M. Wibmer.◻
Definition 3.36. A morphism 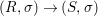 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is smooth (resp. unramified, étale), if it is of finite
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is smooth (resp. unramified, étale), if it is of finite ![]() ${\it\sigma}$-type and formally smooth (resp. formally unramified, formally étale).
${\it\sigma}$-type and formally smooth (resp. formally unramified, formally étale).
Proposition 3.37. If 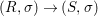 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is ![]() ${\it\sigma}$-pro-étale, then
${\it\sigma}$-pro-étale, then 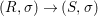 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is étale.
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is étale.
Proof. Assuming that ![]() $(S,{\it\sigma})$ is
$(S,{\it\sigma})$ is ![]() ${\it\sigma}$-pro-étale over
${\it\sigma}$-pro-étale over ![]() $(R,{\it\sigma})$, we can find a system of
$(R,{\it\sigma})$, we can find a system of ![]() $S_{i}$ directed by inclusions
$S_{i}$ directed by inclusions 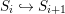 $S_{i}{\hookrightarrow}S_{i+1}$ and homomorphisms
$S_{i}{\hookrightarrow}S_{i+1}$ and homomorphisms 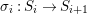 ${\it\sigma}_{i}:S_{i}\rightarrow S_{i+1}$ such that
${\it\sigma}_{i}:S_{i}\rightarrow S_{i+1}$ such that ![]() $(S,{\it\sigma})$ is the direct limit of the
$(S,{\it\sigma})$ is the direct limit of the ![]() $S_{i}$ and the
$S_{i}$ and the ![]() ${\it\sigma}_{i}$, as in Subsection 3.1, where all
${\it\sigma}_{i}$, as in Subsection 3.1, where all ![]() $R\rightarrow S_{i}$ are étale. Suppose we have a situation from 3.28, and write
$R\rightarrow S_{i}$ are étale. Suppose we have a situation from 3.28, and write 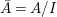 $\bar{A}=A/I$,
$\bar{A}=A/I$, 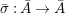 $\bar{{\it\sigma}}:\bar{A}\rightarrow \bar{A}$ for the endomorphism induced by
$\bar{{\it\sigma}}:\bar{A}\rightarrow \bar{A}$ for the endomorphism induced by 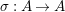 ${\it\sigma}:A\rightarrow A$, and denote the morphism
${\it\sigma}:A\rightarrow A$, and denote the morphism 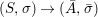 $(S,{\it\sigma})\rightarrow (\bar{A},\bar{{\it\sigma}})$ by
$(S,{\it\sigma})\rightarrow (\bar{A},\bar{{\it\sigma}})$ by ![]() $f$. We obtain the solid part of the diagram
$f$. We obtain the solid part of the diagram
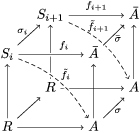
where ![]() $f_{i}$ denotes the restriction of
$f_{i}$ denotes the restriction of ![]() $f$ to
$f$ to ![]() $S_{i}$. The dashed arrows represent the unique lifts
$S_{i}$. The dashed arrows represent the unique lifts 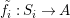 $\tilde{f}_{i}:S_{i}\rightarrow A$ of
$\tilde{f}_{i}:S_{i}\rightarrow A$ of ![]() $f_{i}$. Since both
$f_{i}$. Since both ![]() $\tilde{f}_{i+1}{\it\sigma}_{i}$ and
$\tilde{f}_{i+1}{\it\sigma}_{i}$ and ![]() ${\it\sigma}\tilde{f}_{i}$ are lifts of
${\it\sigma}\tilde{f}_{i}$ are lifts of 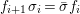 $f_{i+1}{\it\sigma}_{i}=\bar{{\it\sigma}}f_{i}$, by étaleness of
$f_{i+1}{\it\sigma}_{i}=\bar{{\it\sigma}}f_{i}$, by étaleness of ![]() $R\rightarrow S_{i}$ we deduce that
$R\rightarrow S_{i}$ we deduce that 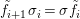 $\tilde{f}_{i+1}{\it\sigma}_{i}={\it\sigma}\tilde{f}_{i}$, which yields a unique lift
$\tilde{f}_{i+1}{\it\sigma}_{i}={\it\sigma}\tilde{f}_{i}$, which yields a unique lift 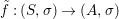 $\tilde{f}:(S,{\it\sigma})\rightarrow (A,{\it\sigma})$ of
$\tilde{f}:(S,{\it\sigma})\rightarrow (A,{\it\sigma})$ of ![]() $f$ in the limit.◻
$f$ in the limit.◻
Definition 3.38. A morphism 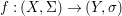 $f:(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ is called smooth (resp. unramified, étale), if it is of finite transformal type and for every
$f:(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ is called smooth (resp. unramified, étale), if it is of finite transformal type and for every ![]() $x\in X$ and every
$x\in X$ and every ![]() ${\it\tau}\in {\rm\Sigma}_{x}$, the morphism
${\it\tau}\in {\rm\Sigma}_{x}$, the morphism 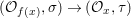 $({\mathcal{O}}_{f(x)},{\it\sigma})\rightarrow ({\mathcal{O}}_{x},{\it\tau})$ is smooth (resp. unramified, étale).
$({\mathcal{O}}_{f(x)},{\it\sigma})\rightarrow ({\mathcal{O}}_{x},{\it\tau})$ is smooth (resp. unramified, étale).
Remark 3.39. A morphism 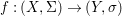 $f:(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ of finite transformal type is unramified (resp. étale) if and only if for every
$f:(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ of finite transformal type is unramified (resp. étale) if and only if for every ![]() $x\in X$ there exists an (affine) open neighborhood on which
$x\in X$ there exists an (affine) open neighborhood on which ![]() $f$ is modeled by an unramified (resp. étale) morphism of difference rings. More precisely, if a morphism
$f$ is modeled by an unramified (resp. étale) morphism of difference rings. More precisely, if a morphism 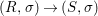 $(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is unramified (resp. étale) at some
$(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ is unramified (resp. étale) at some 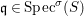 $\mathfrak{q}\in \text{Spec}^{{\it\sigma}}(S)$ lying over
$\mathfrak{q}\in \text{Spec}^{{\it\sigma}}(S)$ lying over 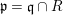 $\mathfrak{p}=\mathfrak{q}\cap R$, then there is a
$\mathfrak{p}=\mathfrak{q}\cap R$, then there is a ![]() $g\notin \mathfrak{q}$ such that the
$g\notin \mathfrak{q}$ such that the ![]() ${\it\sigma}$-localization
${\it\sigma}$-localization 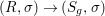 $(R,{\it\sigma})\rightarrow (S_{g},{\it\sigma})$ is unramified (resp. étale).
$(R,{\it\sigma})\rightarrow (S_{g},{\it\sigma})$ is unramified (resp. étale).
The above “openness” statement for the property of being unramified is obvious from 3.33 and 3.32. For étaleness, it follows from 3.32 and the Jacobian criterion for smoothness which states the following. Let ![]() $(A,{\it\sigma})$ be a difference ring,
$(A,{\it\sigma})$ be a difference ring, ![]() $(B,{\it\sigma})$ a formally smooth
$(B,{\it\sigma})$ a formally smooth ![]() $(A,{\it\sigma})$-algebra,
$(A,{\it\sigma})$-algebra, ![]() $J$ a reflexive difference ideal of
$J$ a reflexive difference ideal of ![]() $B$ and let
$B$ and let 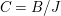 $C=B/J$. Then
$C=B/J$. Then ![]() $(C,{\it\sigma})$ is a formally smooth
$(C,{\it\sigma})$ is a formally smooth ![]() $(A,{\it\sigma})$-algebra if and only if the natural morphism of difference modules
$(A,{\it\sigma})$-algebra if and only if the natural morphism of difference modules
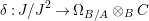 $$\begin{eqnarray}{\it\delta}:J/J^{2}\rightarrow {\rm\Omega}_{B/A}\otimes _{B}C\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}:J/J^{2}\rightarrow {\rm\Omega}_{B/A}\otimes _{B}C\end{eqnarray}$$is left-invertible. We omit the details of the proof since these results will not be used in the sequel. However, a generic étaleness result can be deduced by combining 3.8 with 3.37.
3.4 Étale Galois covers
In view of Babbitt’s decomposition discussed in the next section, many considerations reduce to a study of unramified or étale morphisms with stronger finiteness assumptions such as quasifiniteness or finiteness, and we make every effort to explicitly state them when possible.
Suppose ![]() $(G,\tilde{{\rm\Sigma}})$ acts on
$(G,\tilde{{\rm\Sigma}})$ acts on ![]() $(X,{\rm\Sigma})$. For
$(X,{\rm\Sigma})$. For ![]() $x\in X$, the decomposition group at
$x\in X$, the decomposition group at ![]() $x$ is the stabilizer
$x$ is the stabilizer 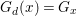 $G_{d}(x)=G_{x}$ of
$G_{d}(x)=G_{x}$ of ![]() $x$. With the notation of 2.22,
$x$. With the notation of 2.22, 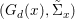 $(G_{d}(x),\tilde{{\rm\Sigma}}_{x})$ acts on
$(G_{d}(x),\tilde{{\rm\Sigma}}_{x})$ acts on 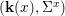 $(\mathbf{k}(x),{\rm\Sigma}^{x})$ and the inertia group
$(\mathbf{k}(x),{\rm\Sigma}^{x})$ and the inertia group ![]() $G_{i}(x)$ at
$G_{i}(x)$ at ![]() $x$ is the set of elements of
$x$ is the set of elements of ![]() $G_{d}(x)$ which act trivially on
$G_{d}(x)$ which act trivially on ![]() $\mathbf{k}(x)$.
$\mathbf{k}(x)$.
If 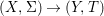 $(X,{\rm\Sigma})\rightarrow (Y,T)$ is a Galois cover with group
$(X,{\rm\Sigma})\rightarrow (Y,T)$ is a Galois cover with group ![]() $(G,\tilde{{\rm\Sigma}})$, and
$(G,\tilde{{\rm\Sigma}})$, and ![]() $(F,{\it\varphi})$ is an algebraically closed difference field, we have that
$(F,{\it\varphi})$ is an algebraically closed difference field, we have that 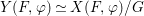 $Y(F,{\it\varphi})\simeq X(F,{\it\varphi})/G$. Moreover, if
$Y(F,{\it\varphi})\simeq X(F,{\it\varphi})/G$. Moreover, if ![]() $x$ is the locus of
$x$ is the locus of 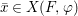 $\bar{x}\in X(F,{\it\varphi})$, the stabilizer of
$\bar{x}\in X(F,{\it\varphi})$, the stabilizer of ![]() $\bar{x}$ in
$\bar{x}$ in ![]() $G$ is exactly the inertia group
$G$ is exactly the inertia group ![]() $G_{i}(x)$.
$G_{i}(x)$.
Proposition 3.40. Suppose that 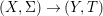 $(X,{\rm\Sigma})\rightarrow (Y,T)$ is a Galois cover of difference schemes of finite transformal type over a difference field
$(X,{\rm\Sigma})\rightarrow (Y,T)$ is a Galois cover of difference schemes of finite transformal type over a difference field ![]() $(k,{\it\sigma})$ with group
$(k,{\it\sigma})$ with group ![]() $(G,\tilde{{\rm\Sigma}})$. If
$(G,\tilde{{\rm\Sigma}})$. If 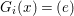 $G_{i}(x)=(e)$ for all
$G_{i}(x)=(e)$ for all ![]() $x\in X$, the natural projection
$x\in X$, the natural projection 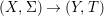 $(X,{\rm\Sigma})\rightarrow (Y,T)$ is finite étale.
$(X,{\rm\Sigma})\rightarrow (Y,T)$ is finite étale.
Proof. Since the assertion is local, we may assume that ![]() $X$ is affine and that we are in the situation of 2.22. Suppose
$X$ is affine and that we are in the situation of 2.22. Suppose 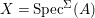 $X=\text{Spec}^{{\rm\Sigma}}(A)$ and that
$X=\text{Spec}^{{\rm\Sigma}}(A)$ and that ![]() $(G,\tilde{{\rm\Sigma}})$ acts on
$(G,\tilde{{\rm\Sigma}})$ acts on ![]() $(A,{\rm\Sigma})$. By assumption, there is a finite tuple
$(A,{\rm\Sigma})$. By assumption, there is a finite tuple ![]() $a\in A$ so that
$a\in A$ so that 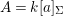 $A=k[a]_{{\rm\Sigma}}$. Writing
$A=k[a]_{{\rm\Sigma}}$. Writing 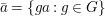 $\bar{a}=\{ga:g\in G\}$, we have that
$\bar{a}=\{ga:g\in G\}$, we have that 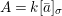 $A=k[\bar{a}]_{{\it\sigma}}$ for any choice of
$A=k[\bar{a}]_{{\it\sigma}}$ for any choice of ![]() ${\it\sigma}\in {\rm\Sigma}$. Then
${\it\sigma}\in {\rm\Sigma}$. Then ![]() $G$ acts on each
$G$ acts on each 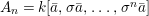 $A_{n}=k[\bar{a},{\it\sigma}\bar{a},\ldots ,{\it\sigma}^{n}\bar{a}]$, and we can form
$A_{n}=k[\bar{a},{\it\sigma}\bar{a},\ldots ,{\it\sigma}^{n}\bar{a}]$, and we can form 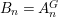 $B_{n}=A_{n}^{G}$. We have
$B_{n}=A_{n}^{G}$. We have 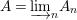 $A=\xrightarrow[]{\lim }_{n}A_{n}$ and
$A=\xrightarrow[]{\lim }_{n}A_{n}$ and 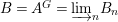 $B=A^{G}=\xrightarrow[]{\lim }_{n}B_{n}$ and we have formed a projective limit of Galois covers
$B=A^{G}=\xrightarrow[]{\lim }_{n}B_{n}$ and we have formed a projective limit of Galois covers 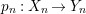 $p_{n}:X_{n}\rightarrow Y_{n}$ such that
$p_{n}:X_{n}\rightarrow Y_{n}$ such that ![]() $X\rightarrow Y$ is obtained by taking the
$X\rightarrow Y$ is obtained by taking the ![]() ${\rm\Sigma}$-fixed points of the ambient Galois cover
${\rm\Sigma}$-fixed points of the ambient Galois cover 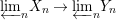 $\xleftarrow[]{\lim }_{n}X_{n}\rightarrow \xleftarrow[]{\lim }_{n}Y_{n}$. Let
$\xleftarrow[]{\lim }_{n}X_{n}\rightarrow \xleftarrow[]{\lim }_{n}Y_{n}$. Let ![]() $x\in X$ and write
$x\in X$ and write ![]() $x_{n}$ for the projection of
$x_{n}$ for the projection of ![]() $x$ in
$x$ in ![]() $X_{n}$. Since
$X_{n}$. Since 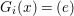 $G_{i}(x)=(e)$, we have that
$G_{i}(x)=(e)$, we have that 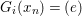 $G_{i}(x_{n})=(e)$ for all
$G_{i}(x_{n})=(e)$ for all ![]() $n$, so by the known result for Galois covers of locally Noetherian schemes it follows that
$n$, so by the known result for Galois covers of locally Noetherian schemes it follows that ![]() $p_{n}$ is étale at
$p_{n}$ is étale at ![]() $x_{n}$. By compatibility of formal étaleness with limits, we conclude that
$x_{n}$. By compatibility of formal étaleness with limits, we conclude that ![]() $X\rightarrow Y$ is étale at
$X\rightarrow Y$ is étale at ![]() $x$.◻
$x$.◻
Corollary 3.41. Suppose ![]() $(X,{\rm\Sigma})$ is integral and that
$(X,{\rm\Sigma})$ is integral and that ![]() $(G,\tilde{{\rm\Sigma}})$ acts faithfully. Then
$(G,\tilde{{\rm\Sigma}})$ acts faithfully. Then  $X\rightarrow X/G$ is étale if and only if all the inertia groups of points of
$X\rightarrow X/G$ is étale if and only if all the inertia groups of points of ![]() $X$ are trivial.
$X$ are trivial.
Proof. By the previous result, it suffices to show that if the quotient morphism is étale at ![]() $x\in X$, then
$x\in X$, then 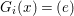 $G_{i}(x)=(e)$. Take an
$G_{i}(x)=(e)$. Take an ![]() $x\in X$ with
$x\in X$ with 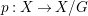 $p:X\rightarrow X/G$ étale. We can easily reduce to the case where
$p:X\rightarrow X/G$ étale. We can easily reduce to the case where 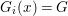 $G_{i}(x)=G$ and
$G_{i}(x)=G$ and 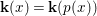 $\mathbf{k}(x)=\mathbf{k}(p(x))$. Note, since
$\mathbf{k}(x)=\mathbf{k}(p(x))$. Note, since ![]() $X$ is integral and
$X$ is integral and ![]() $G$ is faithful on
$G$ is faithful on ![]() $X$, then
$X$, then ![]() $G$ is also faithful on
$G$ is also faithful on ![]() ${\mathcal{O}}_{x}$. However, the classical proof works for the finite local étale extension
${\mathcal{O}}_{x}$. However, the classical proof works for the finite local étale extension 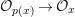 ${\mathcal{O}}_{p(x)}\rightarrow {\mathcal{O}}_{x}$ and shows that
${\mathcal{O}}_{p(x)}\rightarrow {\mathcal{O}}_{x}$ and shows that ![]() $G=(e)$.◻
$G=(e)$.◻
Definition 3.42. A difference scheme ![]() $(X,{\rm\Sigma})$ is faithful if
$(X,{\rm\Sigma})$ is faithful if ![]() ${\rm\Sigma}$ acts faithfully on geometric points of
${\rm\Sigma}$ acts faithfully on geometric points of ![]() $X$ in the sense that, for every geometric point
$X$ in the sense that, for every geometric point 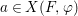 $a\in X(F,{\it\varphi})$, and
$a\in X(F,{\it\varphi})$, and 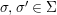 ${\it\sigma},{\it\sigma}^{\prime }\in {\rm\Sigma}$, the relation
${\it\sigma},{\it\sigma}^{\prime }\in {\rm\Sigma}$, the relation 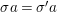 ${\it\sigma}a={\it\sigma}^{\prime }a$ implies
${\it\sigma}a={\it\sigma}^{\prime }a$ implies ![]() ${\it\sigma}={\it\sigma}^{\prime }$.
${\it\sigma}={\it\sigma}^{\prime }$.
Corollary 3.43. Suppose ![]() $(Y,T)$ is faithful, and that
$(Y,T)$ is faithful, and that 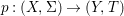 $p:(X,{\rm\Sigma})\rightarrow (Y,T)$ is an étale almost direct Galois cover of transformally integral difference schemes. Then
$p:(X,{\rm\Sigma})\rightarrow (Y,T)$ is an étale almost direct Galois cover of transformally integral difference schemes. Then ![]() $(X,{\rm\Sigma})$ is also faithful.
$(X,{\rm\Sigma})$ is also faithful.
Thus, if 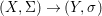 $(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ is an étale Galois cover of a strict difference scheme, then
$(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ is an étale Galois cover of a strict difference scheme, then ![]() $(X,{\rm\Sigma})$ is automatically faithful. Since most generalized difference schemes that appear in the later sections will in fact be Galois covers of a strict difference scheme, we shall not need to discuss faithfulness outside this section.
$(X,{\rm\Sigma})$ is automatically faithful. Since most generalized difference schemes that appear in the later sections will in fact be Galois covers of a strict difference scheme, we shall not need to discuss faithfulness outside this section.
When ![]() $(X,{\rm\Sigma})$ is faithful and
$(X,{\rm\Sigma})$ is faithful and 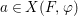 $a\in X(F,{\it\varphi})$ is a geometric point, we define the local
$a\in X(F,{\it\varphi})$ is a geometric point, we define the local ![]() ${\it\varphi}$-substitution
${\it\varphi}$-substitution ![]() ${\it\varphi}_{a}$at
${\it\varphi}_{a}$at ![]() $a$ as the unique element
$a$ as the unique element 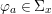 ${\it\varphi}_{a}\in {\rm\Sigma}_{x}$ satisfying
${\it\varphi}_{a}\in {\rm\Sigma}_{x}$ satisfying
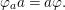 $$\begin{eqnarray}{\it\varphi}_{a}a=a{\it\varphi}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}_{a}a=a{\it\varphi}.\end{eqnarray}$$ In other words, if ![]() $a$ is localized at
$a$ is localized at ![]() $x\in X$, then
$x\in X$, then ![]() ${\it\varphi}_{a}$ is the element of
${\it\varphi}_{a}$ is the element of ![]() ${\rm\Sigma}_{x}$ corresponding (via the conclusion of 2.22(3)) to the image
${\rm\Sigma}_{x}$ corresponding (via the conclusion of 2.22(3)) to the image ![]() ${\it\varphi}^{a}$ of
${\it\varphi}^{a}$ of ![]() ${\it\varphi}$ by the morphism of difference structure
${\it\varphi}$ by the morphism of difference structure 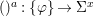 $()^{a}:\{{\it\varphi}\}\rightarrow {\rm\Sigma}^{x}$. Note, when we have a Galois cover
$()^{a}:\{{\it\varphi}\}\rightarrow {\rm\Sigma}^{x}$. Note, when we have a Galois cover 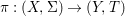 ${\it\pi}:(X,{\rm\Sigma})\rightarrow (Y,T)$ of faithful difference schemes with group
${\it\pi}:(X,{\rm\Sigma})\rightarrow (Y,T)$ of faithful difference schemes with group ![]() $(G,\tilde{{\rm\Sigma}})$, and
$(G,\tilde{{\rm\Sigma}})$, and 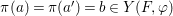 ${\it\pi}(a)={\it\pi}(a^{\prime })=b\in Y(F,{\it\varphi})$, there exists a
${\it\pi}(a)={\it\pi}(a^{\prime })=b\in Y(F,{\it\varphi})$, there exists a ![]() $g\in G$ with
$g\in G$ with ![]() $a^{\prime }=ga$ and
$a^{\prime }=ga$ and
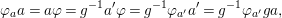 $$\begin{eqnarray}{\it\varphi}_{a}a=a{\it\varphi}=g^{-1}a^{\prime }{\it\varphi}=g^{-1}{\it\varphi}_{a^{\prime }}a^{\prime }=g^{-1}{\it\varphi}_{a^{\prime }}ga,\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}_{a}a=a{\it\varphi}=g^{-1}a^{\prime }{\it\varphi}=g^{-1}{\it\varphi}_{a^{\prime }}a^{\prime }=g^{-1}{\it\varphi}_{a^{\prime }}ga,\end{eqnarray}$$ so we conclude that ![]() ${\it\varphi}_{a}$ and
${\it\varphi}_{a}$ and ![]() ${\it\varphi}_{a^{\prime }}$ are
${\it\varphi}_{a^{\prime }}$ are ![]() $G$-conjugate. Therefore, the following definition is meaningful.
$G$-conjugate. Therefore, the following definition is meaningful.
Definition 3.44. The local ![]() ${\it\varphi}$-substitution at
${\it\varphi}$-substitution at ![]() $b$ is the
$b$ is the ![]() $G$-conjugacy class
$G$-conjugacy class 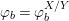 ${\it\varphi}_{b}={\it\varphi}_{b}^{X/Y}$ of any
${\it\varphi}_{b}={\it\varphi}_{b}^{X/Y}$ of any ![]() ${\it\varphi}_{a}$ with
${\it\varphi}_{a}$ with 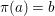 ${\it\pi}(a)=b$.
${\it\pi}(a)=b$.
Alternatively, let 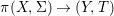 ${\it\pi}(X,{\rm\Sigma})\rightarrow (Y,T)$ be an étale Galois cover, and fix a section
${\it\pi}(X,{\rm\Sigma})\rightarrow (Y,T)$ be an étale Galois cover, and fix a section ![]() $T\rightarrow {\rm\Sigma}$ and a geometric point
$T\rightarrow {\rm\Sigma}$ and a geometric point 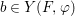 $b\in Y(F,{\it\varphi})$. Writing
$b\in Y(F,{\it\varphi})$. Writing ![]() $\tilde{{\it\sigma}}\in {\rm\Sigma}$ for the image of
$\tilde{{\it\sigma}}\in {\rm\Sigma}$ for the image of 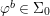 ${\it\varphi}^{b}\in {\rm\Sigma}_{0}$, we define the twisted local
${\it\varphi}^{b}\in {\rm\Sigma}_{0}$, we define the twisted local ![]() ${\it\varphi}$-substitution at
${\it\varphi}$-substitution at 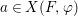 $a\in X(F,{\it\varphi})$ with
$a\in X(F,{\it\varphi})$ with 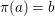 ${\it\pi}(a)=b$, to be the unique element
${\it\pi}(a)=b$, to be the unique element 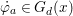 $\dot{{\it\varphi}}_{a}\in G_{d}(x)$ with the property
$\dot{{\it\varphi}}_{a}\in G_{d}(x)$ with the property
 $$\begin{eqnarray}\dot{{\it\varphi}}_{a}\tilde{{\it\sigma}}a=a{\it\varphi}.\end{eqnarray}$$
$$\begin{eqnarray}\dot{{\it\varphi}}_{a}\tilde{{\it\sigma}}a=a{\it\varphi}.\end{eqnarray}$$ As explained above, for 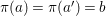 ${\it\pi}(a)={\it\pi}(a^{\prime })=b$, there is a
${\it\pi}(a)={\it\pi}(a^{\prime })=b$, there is a ![]() $g\in G$ such that
$g\in G$ such that
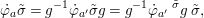 $$\begin{eqnarray}\dot{{\it\varphi}}_{a}\tilde{{\it\sigma}}=g^{-1}\dot{{\it\varphi}}_{a^{\prime }}\tilde{{\it\sigma}}g=g^{-1}\dot{{\it\varphi}}_{a^{\prime }}\,\text{}^{\tilde{{\it\sigma}}}g\,\tilde{{\it\sigma}},\end{eqnarray}$$
$$\begin{eqnarray}\dot{{\it\varphi}}_{a}\tilde{{\it\sigma}}=g^{-1}\dot{{\it\varphi}}_{a^{\prime }}\tilde{{\it\sigma}}g=g^{-1}\dot{{\it\varphi}}_{a^{\prime }}\,\text{}^{\tilde{{\it\sigma}}}g\,\tilde{{\it\sigma}},\end{eqnarray}$$so we can make the following definition.
Definition 3.45. The twisted ![]() ${\it\varphi}$-substitution
${\it\varphi}$-substitution ![]() $\dot{{\it\varphi}}_{b}$ at
$\dot{{\it\varphi}}_{b}$ at 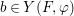 $b\in Y(F,{\it\varphi})$ is the
$b\in Y(F,{\it\varphi})$ is the ![]() $\text{}^{\tilde{{\it\sigma}}}()$-conjugacy class in
$\text{}^{\tilde{{\it\sigma}}}()$-conjugacy class in ![]() $G$ of any
$G$ of any ![]() $\dot{{\it\varphi}}_{a}$ with
$\dot{{\it\varphi}}_{a}$ with 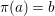 ${\it\pi}(a)=b$.
${\it\pi}(a)=b$.
The previous two definitions are equivalent for an étale Galois cover of faithful difference schemes via the relation 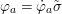 ${\it\varphi}_{a}=\dot{{\it\varphi}}_{a}\tilde{{\it\sigma}}$.
${\it\varphi}_{a}=\dot{{\it\varphi}}_{a}\tilde{{\it\sigma}}$.
In the special case when ![]() $F=\bar{k}$ is the algebraic closure of a finite field
$F=\bar{k}$ is the algebraic closure of a finite field ![]() $k$ and
$k$ and ![]() ${\it\varphi}={\it\varphi}_{k}$ is the Frobenius automorphism generating
${\it\varphi}={\it\varphi}_{k}$ is the Frobenius automorphism generating 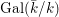 $\text{Gal}(\bar{k}/k)$, and
$\text{Gal}(\bar{k}/k)$, and 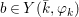 $b\in Y(\bar{k},{\it\varphi}_{k})$ is a
$b\in Y(\bar{k},{\it\varphi}_{k})$ is a ![]() $(\bar{k},{\it\varphi}_{k})$-rational point, we obtain the local Frobenius substitution at
$(\bar{k},{\it\varphi}_{k})$-rational point, we obtain the local Frobenius substitution at ![]() $b$, denoted by
$b$, denoted by ![]() ${\it\varphi}_{k,b}$ when considered as a conjugacy class in
${\it\varphi}_{k,b}$ when considered as a conjugacy class in ![]() ${\rm\Sigma}$, or
${\rm\Sigma}$, or ![]() $\dot{{\it\varphi}}_{k,b}$ when considered as a twisted conjugacy class in
$\dot{{\it\varphi}}_{k,b}$ when considered as a twisted conjugacy class in ![]() $G$.
$G$.
3.5 Transformal separability
The following definition generalizes the notion of ![]() ${\it\sigma}$-separable extensions of difference fields from [Reference Hrushovski18] and [Reference Di Vizio, Hardouin and Wibmer9].
${\it\sigma}$-separable extensions of difference fields from [Reference Hrushovski18] and [Reference Di Vizio, Hardouin and Wibmer9].
(1) An algebra
 $(A,{\rm\Sigma})$ over a difference field
$(A,{\rm\Sigma})$ over a difference field  $(k,{\it\sigma})$ is
$(k,{\it\sigma})$ is  ${\rm\Sigma}$-separable, if
${\rm\Sigma}$-separable, if  $(A,{\rm\Sigma})\otimes _{(k,{\it\sigma})}(k^{\prime },{\it\sigma})$ is
$(A,{\rm\Sigma})\otimes _{(k,{\it\sigma})}(k^{\prime },{\it\sigma})$ is  ${\rm\Sigma}$-reduced/strong for every difference field extension
${\rm\Sigma}$-reduced/strong for every difference field extension  $(k^{\prime },{\it\sigma})$ of
$(k^{\prime },{\it\sigma})$ of  $(k,{\it\sigma})$.
$(k,{\it\sigma})$.(2) A morphism
 $(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ of finite transformal type is transformally separable, if every fiber
$(X,{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ of finite transformal type is transformally separable, if every fiber  $X_{y}$ is a finite union of difference spectra of transformally separable
$X_{y}$ is a finite union of difference spectra of transformally separable  $(\mathbf{k}(y),{\it\sigma}^{y})$-algebras, for
$(\mathbf{k}(y),{\it\sigma}^{y})$-algebras, for  $y\in Y$.
$y\in Y$.(3) A difference field extension
 $(L,{\rm\Sigma})$ of
$(L,{\rm\Sigma})$ of  $(k,{\it\sigma})$ is
$(k,{\it\sigma})$ is  ${\it\tau}$-radicial (for
${\it\tau}$-radicial (for  ${\it\tau}\in {\rm\Sigma}$), if for every
${\it\tau}\in {\rm\Sigma}$), if for every  ${\it\alpha}\in L$, there exists a natural number
${\it\alpha}\in L$, there exists a natural number  $n$ with
$n$ with  ${\it\tau}^{n}{\it\alpha}\in k$. It is
${\it\tau}^{n}{\it\alpha}\in k$. It is  ${\rm\Sigma}$-radicial, if it is
${\rm\Sigma}$-radicial, if it is  ${\it\tau}$-radicial for every
${\it\tau}$-radicial for every  ${\it\tau}\in {\rm\Sigma}$.
${\it\tau}\in {\rm\Sigma}$.(4) A morphism
 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is  ${\it\sigma}$-radicial if it is injective as a map of topological spaces, and for every
${\it\sigma}$-radicial if it is injective as a map of topological spaces, and for every  $x\in X$, the difference field extension
$x\in X$, the difference field extension  $(\mathbf{k}(f(x)),{\it\sigma}^{f(x)})\rightarrow (\mathbf{k}(x),{\it\sigma}^{x})$ is transformally radicial.
$(\mathbf{k}(f(x)),{\it\sigma}^{f(x)})\rightarrow (\mathbf{k}(x),{\it\sigma}^{x})$ is transformally radicial.
Proposition 3.47. Any difference field extension 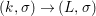 $(k,{\it\sigma})\rightarrow (L,{\it\sigma})$ of finite
$(k,{\it\sigma})\rightarrow (L,{\it\sigma})$ of finite ![]() ${\it\sigma}$-type factors as
${\it\sigma}$-type factors as 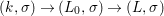 $(k,{\it\sigma})\rightarrow (L_{0},{\it\sigma})\rightarrow (L,{\it\sigma})$, where
$(k,{\it\sigma})\rightarrow (L_{0},{\it\sigma})\rightarrow (L,{\it\sigma})$, where ![]() $L_{0}$ is
$L_{0}$ is ![]() ${\it\sigma}$-separable over
${\it\sigma}$-separable over ![]() $k$, and
$k$, and ![]() $L$ is
$L$ is ![]() ${\it\sigma}$-radicial over
${\it\sigma}$-radicial over ![]() $L_{0}$.
$L_{0}$.
Proof. A subextension ![]() $(E,{\it\sigma})$ is
$(E,{\it\sigma})$ is ![]() ${\it\sigma}$-separable over
${\it\sigma}$-separable over ![]() $k$ if and only if it is linearly disjoint from the inversive closure of
$k$ if and only if it is linearly disjoint from the inversive closure of ![]() $k^{\text{inv}}$ over
$k^{\text{inv}}$ over ![]() $k$. By [Reference Giabicani15, 3.2.9], there is a natural number
$k$. By [Reference Giabicani15, 3.2.9], there is a natural number ![]() $r$ such that
$r$ such that 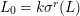 $L_{0}=k{\it\sigma}^{r}(L)$ is linearly disjoint from
$L_{0}=k{\it\sigma}^{r}(L)$ is linearly disjoint from ![]() $k^{\text{inv}}$ over
$k^{\text{inv}}$ over ![]() $k$, that is, such that
$k$, that is, such that ![]() $L_{0}$ is
$L_{0}$ is ![]() ${\it\sigma}$-separable over
${\it\sigma}$-separable over ![]() $k$.◻
$k$.◻
Remark 3.48. A transformally radicial morphism 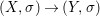 $(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ induces an injection
$(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ induces an injection 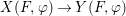 $X(F,{\it\varphi})\rightarrow Y(F,{\it\varphi})$ for every difference field
$X(F,{\it\varphi})\rightarrow Y(F,{\it\varphi})$ for every difference field ![]() $(F,{\it\varphi})$. If
$(F,{\it\varphi})$. If ![]() $(F,{\it\varphi})$ is inversive, the induced map is bijective.
$(F,{\it\varphi})$ is inversive, the induced map is bijective.
Remark 3.49. Let 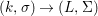 $(k,{\it\sigma})\rightarrow (L,{\rm\Sigma})$ be a difference field extension with
$(k,{\it\sigma})\rightarrow (L,{\rm\Sigma})$ be a difference field extension with ![]() $L/k$ Galois. In view of 2.21,
$L/k$ Galois. In view of 2.21, ![]() $L$ is
$L$ is ![]() ${\it\tau}$-separable (resp.
${\it\tau}$-separable (resp. ![]() ${\it\tau}$-radicial) over
${\it\tau}$-radicial) over ![]() $k$ for some
$k$ for some ![]() ${\it\tau}\in {\rm\Sigma}$ if and only if
${\it\tau}\in {\rm\Sigma}$ if and only if ![]() $L$ is
$L$ is ![]() ${\rm\Sigma}$-separable (resp.
${\rm\Sigma}$-separable (resp. ![]() ${\rm\Sigma}$-radicial) over
${\rm\Sigma}$-radicial) over ![]() $k$.
$k$.
Lemma 3.50. Let 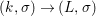 $(k,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a separable,
$(k,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a separable, ![]() ${\it\sigma}$-separable difference field extension, and let
${\it\sigma}$-separable difference field extension, and let ![]() $L_{0}$ be the relative algebraic closure of
$L_{0}$ be the relative algebraic closure of ![]() $k$ in
$k$ in ![]() $L$. Then
$L$. Then ![]() $L$ is regular
$L$ is regular ![]() ${\it\sigma}$-separable over
${\it\sigma}$-separable over ![]() $L_{0}$.
$L_{0}$.
Proof. By [Reference Bourbaki4, Corollary 3, A.V.119], ![]() $L/L_{0}$ is separable and therefore regular. Note, since
$L/L_{0}$ is separable and therefore regular. Note, since ![]() $L_{0}$ is algebraic over
$L_{0}$ is algebraic over ![]() $k$, we have that
$k$, we have that ![]() $L_{0}^{\text{inv}}$ is algebraic over
$L_{0}^{\text{inv}}$ is algebraic over ![]() $k^{\text{inv}}$. Hence, given that
$k^{\text{inv}}$. Hence, given that ![]() $L$ is linearly disjoint from
$L$ is linearly disjoint from ![]() $k^{\text{inv}}$, we deduce that
$k^{\text{inv}}$, we deduce that ![]() $L$ s free from
$L$ s free from ![]() $L_{0}^{\text{inv}}$ over
$L_{0}^{\text{inv}}$ over ![]() $L_{0}$, so [Reference Bourbaki4, Corollary 1, A.V.137] yields that
$L_{0}$, so [Reference Bourbaki4, Corollary 1, A.V.137] yields that ![]() $L$ is linearly disjoint from
$L$ is linearly disjoint from ![]() $L_{0}^{\text{inv}}$ over
$L_{0}^{\text{inv}}$ over ![]() $L_{0}$.◻
$L_{0}$.◻
4 Bi-fibered structure of the category of difference schemes
Definition 4.1. (Pullback)
Let ![]() $(Y,T)$ be a difference scheme and let
$(Y,T)$ be a difference scheme and let 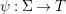 ${\it\psi}:{\rm\Sigma}\rightarrow T$ be a
${\it\psi}:{\rm\Sigma}\rightarrow T$ be a ![]() $\mathit{Diff}$-morphism. The pullback of
$\mathit{Diff}$-morphism. The pullback of ![]() $Y$ with respect to
$Y$ with respect to ![]() ${\it\psi}$ is defined as
${\it\psi}$ is defined as
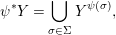 $$\begin{eqnarray}{\it\psi}^{\ast }Y=\mathop{\bigcup }_{{\it\sigma}\in {\rm\Sigma}}Y^{{\it\psi}({\it\sigma})},\end{eqnarray}$$
$$\begin{eqnarray}{\it\psi}^{\ast }Y=\mathop{\bigcup }_{{\it\sigma}\in {\rm\Sigma}}Y^{{\it\psi}({\it\sigma})},\end{eqnarray}$$ with its induced structure as a ![]() ${\rm\Sigma}$-difference scheme, with
${\rm\Sigma}$-difference scheme, with ![]() ${\it\sigma}\in {\rm\Sigma}$ acting as
${\it\sigma}\in {\rm\Sigma}$ acting as ![]() ${\it\psi}({\it\sigma})$ on
${\it\psi}({\it\sigma})$ on ![]() $Y$. There is a natural morphism
$Y$. There is a natural morphism
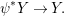 $$\begin{eqnarray}{\it\psi}^{\ast }Y\rightarrow Y.\end{eqnarray}$$
$$\begin{eqnarray}{\it\psi}^{\ast }Y\rightarrow Y.\end{eqnarray}$$Definition 4.2. Let 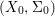 $(X_{0},{\rm\Sigma}_{0})$ be a difference scheme and let
$(X_{0},{\rm\Sigma}_{0})$ be a difference scheme and let 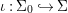 ${\it\iota}:{\rm\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}$ be an inclusion of almost-strict difference structures, that is,
${\it\iota}:{\rm\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}$ be an inclusion of almost-strict difference structures, that is, 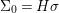 ${\rm\Sigma}_{0}=H{\it\sigma}$,
${\rm\Sigma}_{0}=H{\it\sigma}$, 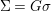 ${\rm\Sigma}=G{\it\sigma}$, and we have a homomorphism
${\rm\Sigma}=G{\it\sigma}$, and we have a homomorphism 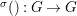 $\text{}^{{\it\sigma}}():G\rightarrow G$, so that
$\text{}^{{\it\sigma}}():G\rightarrow G$, so that ![]() $H$ is a subgroup of
$H$ is a subgroup of ![]() $G$ with
$G$ with 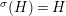 $\text{}^{{\it\sigma}}(H)=H$. Note that in this geometric situation, we have properties dual to those of 2.5(3), namely
$\text{}^{{\it\sigma}}(H)=H$. Note that in this geometric situation, we have properties dual to those of 2.5(3), namely 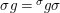 ${\it\sigma}g=\text{}^{{\it\sigma}}g{\it\sigma}$ and
${\it\sigma}g=\text{}^{{\it\sigma}}g{\it\sigma}$ and 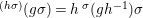 $\text{}^{(h{\it\sigma})}(g{\it\sigma})=h\,\text{}^{{\it\sigma}}(gh^{-1}){\it\sigma}$, for
$\text{}^{(h{\it\sigma})}(g{\it\sigma})=h\,\text{}^{{\it\sigma}}(gh^{-1}){\it\sigma}$, for 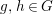 $g,h\in G$.
$g,h\in G$.
For 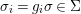 ${\it\sigma}_{i}=g_{i}{\it\sigma}\in {\rm\Sigma}$,
${\it\sigma}_{i}=g_{i}{\it\sigma}\in {\rm\Sigma}$,  $i=0,1,2$, we introduce the notation
$i=0,1,2$, we introduce the notation
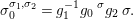 $$\begin{eqnarray}{\it\sigma}_{0}^{{\it\sigma}_{1},{\it\sigma}_{2}}=g_{1}^{-1}g_{0}\,\text{}^{{\it\sigma}}g_{2}\,{\it\sigma}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\sigma}_{0}^{{\it\sigma}_{1},{\it\sigma}_{2}}=g_{1}^{-1}g_{0}\,\text{}^{{\it\sigma}}g_{2}\,{\it\sigma}.\end{eqnarray}$$ Let ![]() $g_{i}$,
$g_{i}$, ![]() $i\in I$ be the representatives of
$i\in I$ be the representatives of ![]() $G/H$, and
$G/H$, and 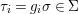 ${\it\tau}_{i}=g_{i}{\it\sigma}\in {\rm\Sigma}$. For each
${\it\tau}_{i}=g_{i}{\it\sigma}\in {\rm\Sigma}$. For each ![]() ${\it\tau}\in {\rm\Sigma}$, and each
${\it\tau}\in {\rm\Sigma}$, and each ![]() ${\it\tau}_{i}$, there is a unique
${\it\tau}_{i}$, there is a unique ![]() ${\it\tau}_{j}$ with
${\it\tau}_{j}$ with 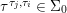 ${\it\tau}^{{\it\tau}_{j},{\it\tau}_{i}}\in {\rm\Sigma}_{0}$. The assignment
${\it\tau}^{{\it\tau}_{j},{\it\tau}_{i}}\in {\rm\Sigma}_{0}$. The assignment ![]() $i\mapsto j$ defines a permutation
$i\mapsto j$ defines a permutation ![]() $\bar{{\it\tau}}$ of
$\bar{{\it\tau}}$ of ![]() $I$. Consider the space
$I$. Consider the space
where each ![]() $X_{i}$ is a copy of
$X_{i}$ is a copy of ![]() $X_{0}$ (that should be thought of as
$X_{0}$ (that should be thought of as ![]() $g_{i}X_{0}$) and
$g_{i}X_{0}$) and ![]() ${\it\tau}\in {\rm\Sigma}$ takes
${\it\tau}\in {\rm\Sigma}$ takes ![]() $X_{i}$ to
$X_{i}$ to ![]() $X_{\bar{{\it\tau}}(i)}$, and acts as
$X_{\bar{{\it\tau}}(i)}$, and acts as 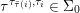 ${\it\tau}^{{\it\tau}_{\bar{{\it\tau}}(i)},{\it\tau}_{i}}\in {\rm\Sigma}_{0}$ on the associated copy of
${\it\tau}^{{\it\tau}_{\bar{{\it\tau}}(i)},{\it\tau}_{i}}\in {\rm\Sigma}_{0}$ on the associated copy of ![]() $X_{0}$. In view of the fact that
$X_{0}$. In view of the fact that ![]() $\bar{{\it\tau}}(i)=i$ if and only if
$\bar{{\it\tau}}(i)=i$ if and only if 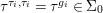 ${\it\tau}^{{\it\tau}_{i},{\it\tau}_{i}}={\it\tau}^{g_{i}}\in {\rm\Sigma}_{0}$, the underlying space of the (coproduct) pushforward is
${\it\tau}^{{\it\tau}_{i},{\it\tau}_{i}}={\it\tau}^{g_{i}}\in {\rm\Sigma}_{0}$, the underlying space of the (coproduct) pushforward is
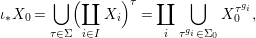 $$\begin{eqnarray}{\it\iota}_{\ast }X_{0}=\mathop{\bigcup }_{{\it\tau}\in {\rm\Sigma}}(\coprod _{i\in I}X_{i})^{{\it\tau}}=\coprod _{i}\mathop{\bigcup }_{{\it\tau}^{g_{i}}\in {\rm\Sigma}_{0}}X_{0}^{{\it\tau}^{g_{i}}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\iota}_{\ast }X_{0}=\mathop{\bigcup }_{{\it\tau}\in {\rm\Sigma}}(\coprod _{i\in I}X_{i})^{{\it\tau}}=\coprod _{i}\mathop{\bigcup }_{{\it\tau}^{g_{i}}\in {\rm\Sigma}_{0}}X_{0}^{{\it\tau}^{g_{i}}},\end{eqnarray}$$ and the action of ![]() ${\rm\Sigma}$ is inherited from
${\rm\Sigma}$ is inherited from 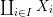 $\coprod _{i\in I}X_{i}$.
$\coprod _{i\in I}X_{i}$.
There is a natural (inclusion) morphism
 $$\begin{eqnarray}(X_{0},{\rm\Sigma}_{0})\rightarrow ({\it\iota}_{\ast }X_{0},{\rm\Sigma}).\end{eqnarray}$$
$$\begin{eqnarray}(X_{0},{\rm\Sigma}_{0})\rightarrow ({\it\iota}_{\ast }X_{0},{\rm\Sigma}).\end{eqnarray}$$Definition 4.3. Let  $(X_{0},{\rm\Sigma}_{0})$ be a difference scheme and let
$(X_{0},{\rm\Sigma}_{0})$ be a difference scheme and let 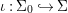 ${\it\iota}:{\rm\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}$ and
${\it\iota}:{\rm\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}$ and ![]() $I$ satisfy the assumptions of 4.2. Consider the space
$I$ satisfy the assumptions of 4.2. Consider the space
where each ![]() $X_{i}$ is a copy of
$X_{i}$ is a copy of ![]() $X_{0}$, which can be identified with
$X_{0}$, which can be identified with ![]() $X_{0}^{I}$, the space of functions
$X_{0}^{I}$, the space of functions 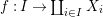 $f:I\rightarrow \coprod _{i\in I}X_{i}$ with the property
$f:I\rightarrow \coprod _{i\in I}X_{i}$ with the property 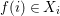 $f(i)\in X_{i}$. The action is defined via
$f(i)\in X_{i}$. The action is defined via
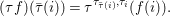 $$\begin{eqnarray}({\it\tau}f)(\bar{{\it\tau}}(i))={\it\tau}^{{\it\tau}_{\bar{{\it\tau}}(i)},{\it\tau}_{i}}(f(i)).\end{eqnarray}$$
$$\begin{eqnarray}({\it\tau}f)(\bar{{\it\tau}}(i))={\it\tau}^{{\it\tau}_{\bar{{\it\tau}}(i)},{\it\tau}_{i}}(f(i)).\end{eqnarray}$$The underlying space of the (product) pushforward is
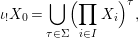 $$\begin{eqnarray}{\it\iota}_{!}X_{0}=\mathop{\bigcup }_{{\it\tau}\in {\rm\Sigma}}(\mathop{\prod }_{i\in I}X_{i})^{{\it\tau}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\iota}_{!}X_{0}=\mathop{\bigcup }_{{\it\tau}\in {\rm\Sigma}}(\mathop{\prod }_{i\in I}X_{i})^{{\it\tau}},\end{eqnarray}$$ and the action of ![]() ${\rm\Sigma}$ is inherited from
${\rm\Sigma}$ is inherited from 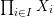 $\prod _{i\in I}X_{i}$.
$\prod _{i\in I}X_{i}$.
There is a natural morphism projecting onto the first factor
 $$\begin{eqnarray}{\it\iota}^{\ast }{\it\iota}_{!}X_{0}\rightarrow X_{0}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\iota}^{\ast }{\it\iota}_{!}X_{0}\rightarrow X_{0}.\end{eqnarray}$$ Definitions 4.2 and 4.3 can also be made sense of in the context of full difference structures ![]() ${\rm\Sigma}$, recall [Reference Tomašić24, 2.6].
${\rm\Sigma}$, recall [Reference Tomašić24, 2.6].
Definition 4.4. Let ![]() $(X,{\rm\Sigma})$ be a difference scheme and let
$(X,{\rm\Sigma})$ be a difference scheme and let 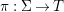 ${\it\pi}:{\rm\Sigma}\rightarrow T$ be a
${\it\pi}:{\rm\Sigma}\rightarrow T$ be a ![]() $\mathit{Diff}$-morphism such that there exists a finite group
$\mathit{Diff}$-morphism such that there exists a finite group ![]() $K$ acting faithfully on
$K$ acting faithfully on ![]() ${\rm\Sigma}$ such that
${\rm\Sigma}$ such that ![]() ${\it\pi}$ is in fact the canonical projection
${\it\pi}$ is in fact the canonical projection 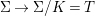 ${\rm\Sigma}\rightarrow {\rm\Sigma}/K=T$. We define
${\rm\Sigma}\rightarrow {\rm\Sigma}/K=T$. We define
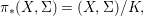 $$\begin{eqnarray}{\it\pi}_{\ast }(X,{\rm\Sigma})=(X,{\rm\Sigma})/K,\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{\ast }(X,{\rm\Sigma})=(X,{\rm\Sigma})/K,\end{eqnarray}$$ considered as a ![]() $T$-difference scheme. There is an obvious quotient morphism
$T$-difference scheme. There is an obvious quotient morphism
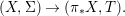 $$\begin{eqnarray}(X,{\rm\Sigma})\rightarrow ({\it\pi}_{\ast }X,T).\end{eqnarray}$$
$$\begin{eqnarray}(X,{\rm\Sigma})\rightarrow ({\it\pi}_{\ast }X,T).\end{eqnarray}$$Remark 4.5. Let 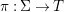 ${\it\pi}:{\rm\Sigma}\rightarrow T$ be as in 4.4. We shall not need the functor
${\it\pi}:{\rm\Sigma}\rightarrow T$ be as in 4.4. We shall not need the functor ![]() ${\it\pi}_{!}$ in the sequel, but we give an idea of its construction on an affine model. Let
${\it\pi}_{!}$ in the sequel, but we give an idea of its construction on an affine model. Let ![]() $(R,{\rm\Sigma})$ be a difference algebra over a difference field
$(R,{\rm\Sigma})$ be a difference algebra over a difference field ![]() $(k,{\it\varphi})$. Let
$(k,{\it\varphi})$. Let
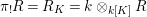 $$\begin{eqnarray}{\it\pi}_{!}R=R_{K}=k\otimes _{k[K]}R\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{!}R=R_{K}=k\otimes _{k[K]}R\end{eqnarray}$$ be the ring of ![]() $K$-coinvariants, with its natural
$K$-coinvariants, with its natural ![]() $T$-action. Both natural morphisms
$T$-action. Both natural morphisms 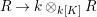 $R\rightarrow k\otimes _{k[K]}R$ and
$R\rightarrow k\otimes _{k[K]}R$ and 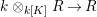 $k\otimes _{k[K]}R\rightarrow R$ are used to prove the required adjunction below.
$k\otimes _{k[K]}R\rightarrow R$ are used to prove the required adjunction below.
Definition 4.6. Let ![]() $(X,{\rm\Sigma})$ be a difference scheme and let
$(X,{\rm\Sigma})$ be a difference scheme and let 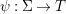 ${\it\psi}:{\rm\Sigma}\rightarrow T$ be a
${\it\psi}:{\rm\Sigma}\rightarrow T$ be a ![]() $\mathit{Diff}$-morphism which is a composite of
$\mathit{Diff}$-morphism which is a composite of ![]() $\mathit{Diff}$-morphisms satisfying the requirements of 4.2 or 4.4,
$\mathit{Diff}$-morphisms satisfying the requirements of 4.2 or 4.4,  ${\it\psi}={\it\psi}_{1}\circ \cdots {\it\psi}_{n}$. We define
${\it\psi}={\it\psi}_{1}\circ \cdots {\it\psi}_{n}$. We define
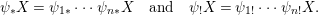 $$\begin{eqnarray}{\it\psi}_{\ast }X={\it\psi}_{1\ast }\cdots {\it\psi}_{n\ast }X\quad \text{and}\quad {\it\psi}_{!}X={\it\psi}_{1!}\cdots {\it\psi}_{n!}X.\end{eqnarray}$$
$$\begin{eqnarray}{\it\psi}_{\ast }X={\it\psi}_{1\ast }\cdots {\it\psi}_{n\ast }X\quad \text{and}\quad {\it\psi}_{!}X={\it\psi}_{1!}\cdots {\it\psi}_{n!}X.\end{eqnarray}$$Theorem 4.7. Let 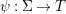 ${\it\psi}:{\rm\Sigma}\rightarrow T$ be a
${\it\psi}:{\rm\Sigma}\rightarrow T$ be a ![]() $\mathit{Diff}$-morphism as in 4.6.
$\mathit{Diff}$-morphism as in 4.6.
(1) The functor
 ${\it\psi}_{\ast }$ is left adjoint to
${\it\psi}_{\ast }$ is left adjoint to  ${\it\psi}^{\ast }$, that is, functorially in
${\it\psi}^{\ast }$, that is, functorially in $$\begin{eqnarray}\text{Hom}_{{\rm\Sigma}}(X,{\it\psi}^{\ast }Y)\simeq \text{Hom}_{T}({\it\psi}_{\ast }X,Y),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{{\rm\Sigma}}(X,{\it\psi}^{\ast }Y)\simeq \text{Hom}_{T}({\it\psi}_{\ast }X,Y),\end{eqnarray}$$ $(X,{\rm\Sigma})$ and
$(X,{\rm\Sigma})$ and  $(Y,T)$.
$(Y,T)$.(2) The functor
 ${\it\psi}_{!}$ is right adjoint to
${\it\psi}_{!}$ is right adjoint to  ${\it\psi}^{\ast }$, that is, functorially in
${\it\psi}^{\ast }$, that is, functorially in $$\begin{eqnarray}\text{Hom}_{{\rm\Sigma}}({\it\psi}^{\ast }Y,X)\simeq \text{Hom}_{T}(Y,{\it\psi}_{!}X),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{{\rm\Sigma}}({\it\psi}^{\ast }Y,X)\simeq \text{Hom}_{T}(Y,{\it\psi}_{!}X),\end{eqnarray}$$ $(X,{\rm\Sigma})$ and
$(X,{\rm\Sigma})$ and  $(Y,T)$.
$(Y,T)$.
Proof. (1) Suppose we have a difference scheme ![]() $(X,{\rm\Sigma})$ and
$(X,{\rm\Sigma})$ and 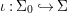 ${\it\iota}:{\rm\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}$ satisfies the assumptions of 4.2. Writing
${\it\iota}:{\rm\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}$ satisfies the assumptions of 4.2. Writing 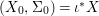 $(X_{0},{\rm\Sigma}_{0})={\it\iota}^{\ast }X$ and adopting the above notation, there is a natural morphism
$(X_{0},{\rm\Sigma}_{0})={\it\iota}^{\ast }X$ and adopting the above notation, there is a natural morphism 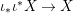 ${\it\iota}_{\ast }{\it\iota}^{\ast }X\rightarrow X$, induced by the morphism
${\it\iota}_{\ast }{\it\iota}^{\ast }X\rightarrow X$, induced by the morphism 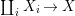 $\coprod _{i}X_{i}\rightarrow X$, taking the
$\coprod _{i}X_{i}\rightarrow X$, taking the ![]() $i\text{th}$ copy of
$i\text{th}$ copy of ![]() $X_{0}$ to
$X_{0}$ to ![]() $g_{i}(X_{0})$. Since
$g_{i}(X_{0})$. Since ![]() ${\it\iota}^{\ast }{\it\iota}_{\ast }Y$ is a disjoint union of copies of
${\it\iota}^{\ast }{\it\iota}_{\ast }Y$ is a disjoint union of copies of ![]() $(Y,{\rm\Sigma}_{0})$, an obvious morphism
$(Y,{\rm\Sigma}_{0})$, an obvious morphism 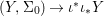 $(Y,{\rm\Sigma}_{0})\rightarrow {\it\iota}^{\ast }{\it\iota}_{\ast }Y$ is the inclusion onto the first copy. This makes it easy to verify that the resulting adjunctions
$(Y,{\rm\Sigma}_{0})\rightarrow {\it\iota}^{\ast }{\it\iota}_{\ast }Y$ is the inclusion onto the first copy. This makes it easy to verify that the resulting adjunctions
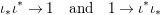 $$\begin{eqnarray}{\it\iota}_{\ast }{\it\iota}^{\ast }\rightarrow 1\quad \text{and}\quad 1\rightarrow {\it\iota}^{\ast }{\it\iota}_{\ast }\end{eqnarray}$$
$$\begin{eqnarray}{\it\iota}_{\ast }{\it\iota}^{\ast }\rightarrow 1\quad \text{and}\quad 1\rightarrow {\it\iota}^{\ast }{\it\iota}_{\ast }\end{eqnarray}$$ indeed satisfy the required unit-counit identities for the required adjunction to hold. When 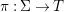 ${\it\pi}:{\rm\Sigma}\rightarrow T$ satisfies the requirements of 4.4,
${\it\pi}:{\rm\Sigma}\rightarrow T$ satisfies the requirements of 4.4, 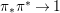 ${\it\pi}_{\ast }{\it\pi}^{\ast }\rightarrow 1$ is an isomorphism and
${\it\pi}_{\ast }{\it\pi}^{\ast }\rightarrow 1$ is an isomorphism and 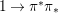 $1\rightarrow {\it\pi}^{\ast }{\it\pi}_{\ast }$ is essentially the quotient morphism, so the unit-counit relations are easily verified.
$1\rightarrow {\it\pi}^{\ast }{\it\pi}_{\ast }$ is essentially the quotient morphism, so the unit-counit relations are easily verified.
(2) With the above notation, a natural morphism 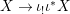 $X\rightarrow {\it\iota}_{!}{\it\iota}^{\ast }X$ is obtained as a restriction of the twisted diagonal embedding
$X\rightarrow {\it\iota}_{!}{\it\iota}^{\ast }X$ is obtained as a restriction of the twisted diagonal embedding 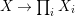 $X\rightarrow \prod _{i}X_{i}$, where the
$X\rightarrow \prod _{i}X_{i}$, where the ![]() $X_{i}$ are copies of
$X_{i}$ are copies of ![]() $X$ and the morphism is
$X$ and the morphism is 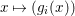 $x\mapsto (g_{i}(x))$. For
$x\mapsto (g_{i}(x))$. For ![]() $(Y,{\rm\Sigma}_{0})$, a natural morphism
$(Y,{\rm\Sigma}_{0})$, a natural morphism 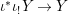 ${\it\iota}^{\ast }{\it\iota}_{!}Y\rightarrow Y$ is the projection on the first factor,
${\it\iota}^{\ast }{\it\iota}_{!}Y\rightarrow Y$ is the projection on the first factor, ![]() ${\it\iota}^{\ast }{\it\iota}_{!}Y$ being a direct product of copies of
${\it\iota}^{\ast }{\it\iota}_{!}Y$ being a direct product of copies of ![]() $(Y,{\rm\Sigma})$. It is just a formality to verify that the resulting adjunctions
$(Y,{\rm\Sigma})$. It is just a formality to verify that the resulting adjunctions
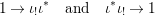 $$\begin{eqnarray}1\rightarrow {\it\iota}_{!}{\it\iota}^{\ast }\quad \text{and}\quad {\it\iota}^{\ast }{\it\iota}_{!}\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow {\it\iota}_{!}{\it\iota}^{\ast }\quad \text{and}\quad {\it\iota}^{\ast }{\it\iota}_{!}\rightarrow 1\end{eqnarray}$$are as required. ◻
Remark 4.8. The construction from 4.3 can be adapted to a relative setting. In addition to the data from 4.3, suppose we have a difference scheme ![]() $(Y,{\rm\Sigma})$ and a morphism
$(Y,{\rm\Sigma})$ and a morphism 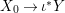 $X_{0}\rightarrow {\it\iota}^{\ast }Y$. We carry out an analogous construction on the fiber product of the
$X_{0}\rightarrow {\it\iota}^{\ast }Y$. We carry out an analogous construction on the fiber product of the ![]() $X_{i}$ over
$X_{i}$ over ![]() $Y$, where
$Y$, where 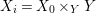 $X_{i}=X_{0}\times _{Y}Y$ as in the diagram
$X_{i}=X_{0}\times _{Y}Y$ as in the diagram
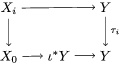
which yields a difference scheme  $({\it\iota}_{!}(X_{0}/Y),{\rm\Sigma})$ satisfying
$({\it\iota}_{!}(X_{0}/Y),{\rm\Sigma})$ satisfying
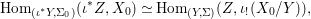 $$\begin{eqnarray}\text{Hom}_{({\it\iota}^{\ast }Y,{\rm\Sigma}_{0})}({\it\iota}^{\ast }Z,X_{0})\simeq \text{Hom}_{(Y,{\rm\Sigma})}(Z,{\it\iota}_{!}(X_{0}/Y)),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{({\it\iota}^{\ast }Y,{\rm\Sigma}_{0})}({\it\iota}^{\ast }Z,X_{0})\simeq \text{Hom}_{(Y,{\rm\Sigma})}(Z,{\it\iota}_{!}(X_{0}/Y)),\end{eqnarray}$$ for any difference scheme ![]() $(Z,{\rm\Sigma})$ over
$(Z,{\rm\Sigma})$ over ![]() $(Y,{\rm\Sigma})$.
$(Y,{\rm\Sigma})$.
Remark 4.9. As hinted in [Reference Tomašić24, 2.10], the functor  $(X,{\rm\Sigma})\mapsto {\rm\Sigma}$ makes the category of difference schemes into a (split) fibered category over
$(X,{\rm\Sigma})\mapsto {\rm\Sigma}$ makes the category of difference schemes into a (split) fibered category over ![]() $\mathit{Diff}$.
$\mathit{Diff}$.
In Grothendieck’s terminology from [Reference Grothendieck17], the existence of left adjoints for the pullback functors makes the category of almost-strict difference schemes into a (split) bi-fibered category over the category of almost-strict difference structures. The author is uncertain on the nomenclature of (split) fibrations in which the pullback functors come with right adjoints as well.
5 Babbitt’s decomposition
5.1 Nonabelian difference Galois cohomology
Definition 5.1. Let ![]() $(G,{\rm\Sigma})$ be a difference group. Recall (2.17), for every
$(G,{\rm\Sigma})$ be a difference group. Recall (2.17), for every ![]() ${\it\sigma}\in {\rm\Sigma}$ we have a group endomorphism
${\it\sigma}\in {\rm\Sigma}$ we have a group endomorphism 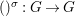 $()^{{\it\sigma}}:G\rightarrow G$ such that for every
$()^{{\it\sigma}}:G\rightarrow G$ such that for every ![]() $g\in G$ and
$g\in G$ and  ${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
${\it\sigma},{\it\tau}\in {\rm\Sigma}$,
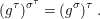 $$\begin{eqnarray}\left(g^{{\it\tau}}\right)^{{\it\sigma}^{{\it\tau}}}=\left(g^{{\it\sigma}}\right)^{{\it\tau}}.\end{eqnarray}$$
$$\begin{eqnarray}\left(g^{{\it\tau}}\right)^{{\it\sigma}^{{\it\tau}}}=\left(g^{{\it\sigma}}\right)^{{\it\tau}}.\end{eqnarray}$$ We let  $H^{0}({\rm\Sigma},G)=G^{{\rm\Sigma}}=\{g\in G:g^{{\it\sigma}}=g\text{ for all }{\it\sigma}\in {\rm\Sigma}\}$. A cocycle is a map
$H^{0}({\rm\Sigma},G)=G^{{\rm\Sigma}}=\{g\in G:g^{{\it\sigma}}=g\text{ for all }{\it\sigma}\in {\rm\Sigma}\}$. A cocycle is a map  $a:{\rm\Sigma}\rightarrow G$ such that
$a:{\rm\Sigma}\rightarrow G$ such that
 $$\begin{eqnarray}a({\it\sigma})^{{\it\tau}}=a({\it\tau})^{{\it\sigma}^{{\it\tau}}}a({\it\sigma}^{{\it\tau}})a({\it\tau})^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}a({\it\sigma})^{{\it\tau}}=a({\it\tau})^{{\it\sigma}^{{\it\tau}}}a({\it\sigma}^{{\it\tau}})a({\it\tau})^{-1}.\end{eqnarray}$$ Two cycles ![]() $a$ and
$a$ and ![]() $b$ are cohomologous, if there exists a
$b$ are cohomologous, if there exists a ![]() $g\in G$ such that
$g\in G$ such that
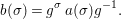 $$\begin{eqnarray}b({\it\sigma})=g^{{\it\sigma}}\,a({\it\sigma})g^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}b({\it\sigma})=g^{{\it\sigma}}\,a({\it\sigma})g^{-1}.\end{eqnarray}$$ The cohomology set  $H^{1}({\rm\Sigma},G)$ is the pointed set of equivalence classes of cocycles by the relation of being cohomologous, equipped with the distinguished class of the unit cocycle.
$H^{1}({\rm\Sigma},G)$ is the pointed set of equivalence classes of cocycles by the relation of being cohomologous, equipped with the distinguished class of the unit cocycle.
Proposition 5.2. Every short exact sequence of ![]() $\mathit{Diff}$-groups
$\mathit{Diff}$-groups
 $$\begin{eqnarray}1\rightarrow (H,{\rm\Sigma})\rightarrow (G,{\rm\Sigma})\rightarrow (\bar{G},{\rm\Sigma})\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow (H,{\rm\Sigma})\rightarrow (G,{\rm\Sigma})\rightarrow (\bar{G},{\rm\Sigma})\rightarrow 1\end{eqnarray}$$gives rise to a long exact cohomology sequence
 $$\begin{eqnarray}\displaystyle & 1\rightarrow H^{0}({\rm\Sigma},H)\rightarrow H^{0}({\rm\Sigma},G)\rightarrow H^{0}({\rm\Sigma},\bar{G})\rightarrow & \displaystyle \nonumber\\ \displaystyle & \rightarrow H^{1}({\rm\Sigma},H)\rightarrow H^{1}({\rm\Sigma},G)\rightarrow H^{1}({\rm\Sigma},\bar{G}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & 1\rightarrow H^{0}({\rm\Sigma},H)\rightarrow H^{0}({\rm\Sigma},G)\rightarrow H^{0}({\rm\Sigma},\bar{G})\rightarrow & \displaystyle \nonumber\\ \displaystyle & \rightarrow H^{1}({\rm\Sigma},H)\rightarrow H^{1}({\rm\Sigma},G)\rightarrow H^{1}({\rm\Sigma},\bar{G}). & \displaystyle \nonumber\end{eqnarray}$$The proof consists of a number of lengthy but routine verifications similar to the proof of an analogous result in classical group/semigroup/rack cohomology.
Remark 5.3. In the case 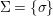 ${\rm\Sigma}=\{{\it\sigma}\}$,
${\rm\Sigma}=\{{\it\sigma}\}$, 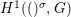 $H^{1}(()^{{\it\sigma}},G)$ is just the set of
$H^{1}(()^{{\it\sigma}},G)$ is just the set of ![]() $()^{{\it\sigma}}$-conjugacy classes in
$()^{{\it\sigma}}$-conjugacy classes in ![]() $G$, so clearly the last arrow in 5.2 is surjective.
$G$, so clearly the last arrow in 5.2 is surjective.
Let 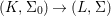 $(K,{\rm\Sigma}_{0})\rightarrow (L,{\rm\Sigma})$ be a separable quasi-Galois extension with a surjective structure morphism
$(K,{\rm\Sigma}_{0})\rightarrow (L,{\rm\Sigma})$ be a separable quasi-Galois extension with a surjective structure morphism 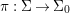 ${\it\pi}:{\rm\Sigma}\rightarrow {\rm\Sigma}_{0}$ and let
${\it\pi}:{\rm\Sigma}\rightarrow {\rm\Sigma}_{0}$ and let 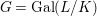 $G=\text{Gal}(L/K)$. The morphism
$G=\text{Gal}(L/K)$. The morphism ![]() ${\it\pi}$ extends to the set
${\it\pi}$ extends to the set ![]() $\hat{{\rm\Sigma}}$ consisting of all lifts of elements of
$\hat{{\rm\Sigma}}$ consisting of all lifts of elements of ![]() ${\rm\Sigma}_{0}$ to
${\rm\Sigma}_{0}$ to ![]() $L$ by the rule
$L$ by the rule 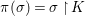 ${\it\pi}({\it\sigma})={\it\sigma}\,\restriction\,K$.
${\it\pi}({\it\sigma})={\it\sigma}\,\restriction\,K$.
As in 2.21, for any 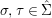 ${\it\sigma},{\it\tau}\in \hat{{\rm\Sigma}}$ such that
${\it\sigma},{\it\tau}\in \hat{{\rm\Sigma}}$ such that 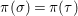 ${\it\pi}({\it\sigma})={\it\pi}({\it\tau})$, there exists a (unique)
${\it\pi}({\it\sigma})={\it\pi}({\it\tau})$, there exists a (unique) ![]() $g\in G$ with
$g\in G$ with ![]() ${\it\tau}={\it\sigma}g$. For each
${\it\tau}={\it\sigma}g$. For each ![]() ${\it\tau}\in {\rm\Sigma}$ this yields a homomorphism
${\it\tau}\in {\rm\Sigma}$ this yields a homomorphism 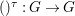 $()^{{\it\tau}}:G\rightarrow G$ such that
$()^{{\it\tau}}:G\rightarrow G$ such that
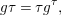 $$\begin{eqnarray}g{\it\tau}={\it\tau}g^{{\it\tau}},\end{eqnarray}$$
$$\begin{eqnarray}g{\it\tau}={\it\tau}g^{{\it\tau}},\end{eqnarray}$$ which makes ![]() $G$ into a
$G$ into a ![]() $\mathit{Diff}$-group
$\mathit{Diff}$-group ![]() $(G,{\rm\Sigma})$.
$(G,{\rm\Sigma})$.
Suppose now ![]() $(L,{\rm\Sigma}^{\prime })$ is another extension of
$(L,{\rm\Sigma}^{\prime })$ is another extension of ![]() $(K,{\rm\Sigma}_{0})$, with
$(K,{\rm\Sigma}_{0})$, with 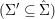 $({\rm\Sigma}^{\prime }\subseteq \hat{{\rm\Sigma}})$ and let
$({\rm\Sigma}^{\prime }\subseteq \hat{{\rm\Sigma}})$ and let 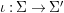 ${\it\iota}:{\rm\Sigma}\rightarrow {\rm\Sigma}^{\prime }$ be a surjective
${\it\iota}:{\rm\Sigma}\rightarrow {\rm\Sigma}^{\prime }$ be a surjective ![]() $\mathit{Diff}$-morphism with the property
$\mathit{Diff}$-morphism with the property ![]() ${\it\pi}{\it\iota}={\it\pi}$. It is easily verified that maps
${\it\pi}{\it\iota}={\it\pi}$. It is easily verified that maps 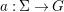 $a:{\rm\Sigma}\rightarrow G$ satisfying
$a:{\rm\Sigma}\rightarrow G$ satisfying
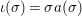 $$\begin{eqnarray}{\it\iota}({\it\sigma})={\it\sigma}a({\it\sigma})\end{eqnarray}$$
$$\begin{eqnarray}{\it\iota}({\it\sigma})={\it\sigma}a({\it\sigma})\end{eqnarray}$$ correspond to cocycles, and that cocycles ![]() $a_{1}$,
$a_{1}$, ![]() $a_{2}$ corresponding to isomorphic extensions
$a_{2}$ corresponding to isomorphic extensions ![]() $(L,{\rm\Sigma}_{1})$,
$(L,{\rm\Sigma}_{1})$, ![]() $(L,{\rm\Sigma}_{2})$ of
$(L,{\rm\Sigma}_{2})$ of ![]() $(K,{\rm\Sigma}_{0})$ are cohomologous. We draw the following conclusion.
$(K,{\rm\Sigma}_{0})$ are cohomologous. We draw the following conclusion.
Remark 5.4. The cohomology set  $H^{1}({\rm\Sigma},\text{Gal}(L/K))$ classifies the above family of difference field extensions of
$H^{1}({\rm\Sigma},\text{Gal}(L/K))$ classifies the above family of difference field extensions of ![]() $(K,{\rm\Sigma}_{0})$ up to isomorphism.
$(K,{\rm\Sigma}_{0})$ up to isomorphism.
5.2 Benign extensions and Babbitt’s theorem
Definition 5.5. A morphism  $(S,{\it\sigma})\rightarrow (R,{\it\sigma})$ of difference rings is called benign if there exists a quasifinite
$(S,{\it\sigma})\rightarrow (R,{\it\sigma})$ of difference rings is called benign if there exists a quasifinite 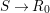 $S\rightarrow R_{0}$ such that
$S\rightarrow R_{0}$ such that ![]() $(R,{\it\sigma})$ is isomorphic to
$(R,{\it\sigma})$ is isomorphic to ![]() $[{\it\sigma}]_{S}R_{0}$ over
$[{\it\sigma}]_{S}R_{0}$ over ![]() $(S,{\it\sigma})$. In other words, writing
$(S,{\it\sigma})$. In other words, writing 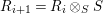 $R_{i+1}=R_{i}\otimes _{S}S$ for
$R_{i+1}=R_{i}\otimes _{S}S$ for ![]() $i\geqslant 0$ (where the morphism
$i\geqslant 0$ (where the morphism ![]() $S\rightarrow S$ is
$S\rightarrow S$ is ![]() ${\it\sigma}$),
${\it\sigma}$), ![]() $(R,{\it\sigma})$ is the (limit) tensor product of the
$(R,{\it\sigma})$ is the (limit) tensor product of the ![]() $R_{i}$ and the canonical morphisms
$R_{i}$ and the canonical morphisms 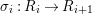 ${\it\sigma}_{i}:R_{i}\rightarrow R_{i+1}$ over
${\it\sigma}_{i}:R_{i}\rightarrow R_{i+1}$ over ![]() $S$. The morphism is proper benign if, in addition,
$S$. The morphism is proper benign if, in addition, ![]() $R$ is (algebraically) integral over
$R$ is (algebraically) integral over ![]() $S$.
$S$.
In the benign Galois case, ![]() $R_{0}$ is Galois over
$R_{0}$ is Galois over ![]() $S$ with group
$S$ with group ![]() $G_{0}$ and the Galois group
$G_{0}$ and the Galois group  $\text{Gal}(R/S)=\text{Gal}(\mathbf{k}(R)/\mathbf{k}(S))=(G,()^{{\it\sigma}})$ is isomorphic to the direct product of
$\text{Gal}(R/S)=\text{Gal}(\mathbf{k}(R)/\mathbf{k}(S))=(G,()^{{\it\sigma}})$ is isomorphic to the direct product of 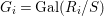 $G_{i}=\text{Gal}(R_{i}/S)$ and
$G_{i}=\text{Gal}(R_{i}/S)$ and ![]() $()^{{\it\sigma}}$ “shifts” from
$()^{{\it\sigma}}$ “shifts” from ![]() $G_{i}$ to
$G_{i}$ to ![]() $G_{i+1}$.
$G_{i+1}$.
In view of such a specific form of ![]() $G$, we the get that for any
$G$, we the get that for any 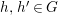 $h,h^{\prime }\in G$ there is a
$h,h^{\prime }\in G$ there is a ![]() $g\in G$ such that
$g\in G$ such that 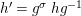 $h^{\prime }=g^{{\it\sigma}}\,hg^{-1}$, that is,
$h^{\prime }=g^{{\it\sigma}}\,hg^{-1}$, that is, ![]() $h$ and
$h$ and ![]() $h^{\prime }$ are
$h^{\prime }$ are ![]() $()^{{\it\sigma}}$-conjugate, proving the following.
$()^{{\it\sigma}}$-conjugate, proving the following.
Lemma 5.6. The (nonabelian) difference cohomology 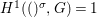 $H^{1}(()^{{\it\sigma}},G)=1$.
$H^{1}(()^{{\it\sigma}},G)=1$.
Lemma 5.7. If ![]() $R$ is proper benign over
$R$ is proper benign over ![]() $S$, then for any
$S$, then for any 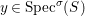 $y\in \text{Spec}^{{\it\sigma}}(S)$, any algebraically closed difference field
$y\in \text{Spec}^{{\it\sigma}}(S)$, any algebraically closed difference field ![]() $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending 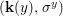 $(\mathbf{k}(y),{\it\sigma}^{y})$, any
$(\mathbf{k}(y),{\it\sigma}^{y})$, any 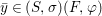 $\bar{y}\in (S,{\it\sigma})(F,{\it\varphi})$ above
$\bar{y}\in (S,{\it\sigma})(F,{\it\varphi})$ above ![]() $y$ and any
$y$ and any ![]() $g\in G$, there exists an
$g\in G$, there exists an 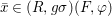 $\bar{x}\in (R,g{\it\sigma})(F,{\it\varphi})$ lifting
$\bar{x}\in (R,g{\it\sigma})(F,{\it\varphi})$ lifting ![]() $\bar{y}$.
$\bar{y}$.
Proof. By 5.6 and 5.4, all ![]() $(R,{\it\sigma}g)$,
$(R,{\it\sigma}g)$, ![]() $g\in G$ are isomorphic over
$g\in G$ are isomorphic over ![]() $(S,{\it\sigma})$, so it suffices to treat the case of
$(S,{\it\sigma})$, so it suffices to treat the case of ![]() $(R,{\it\sigma})$.
$(R,{\it\sigma})$.
Let ![]() $R_{i}$ be as in 5.5. By the integrality assumption, all the
$R_{i}$ be as in 5.5. By the integrality assumption, all the ![]() $R_{i}$ are finite over
$R_{i}$ are finite over ![]() $S$. Let
$S$. Let 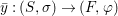 $\bar{y}:(S,{\it\sigma})\rightarrow (F,{\it\varphi})$. Since
$\bar{y}:(S,{\it\sigma})\rightarrow (F,{\it\varphi})$. Since ![]() $R_{0}$ is finite over
$R_{0}$ is finite over ![]() $S$ and
$S$ and ![]() $F$ is algebraically closed, we can find some
$F$ is algebraically closed, we can find some 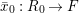 $\bar{x}_{0}:R_{0}\rightarrow F$ above
$\bar{x}_{0}:R_{0}\rightarrow F$ above ![]() $\bar{y}$. By the universal property 3.1 of
$\bar{y}$. By the universal property 3.1 of 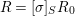 $R=[{\it\sigma}]_{S}R_{0}$, there exists an
$R=[{\it\sigma}]_{S}R_{0}$, there exists an 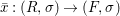 $\bar{x}:(R,{\it\sigma})\rightarrow (F,{\it\sigma})$ extending
$\bar{x}:(R,{\it\sigma})\rightarrow (F,{\it\sigma})$ extending ![]() $\bar{x}_{0}$ and consequently
$\bar{x}_{0}$ and consequently ![]() $\bar{y}$.◻
$\bar{y}$.◻
(1) A morphism
 $({\it\psi},()^{{\it\psi}}):(S,T)\rightarrow (R,{\rm\Sigma})$ of almost-strict difference rings is benign if for some (or equivalently, for all)
$({\it\psi},()^{{\it\psi}}):(S,T)\rightarrow (R,{\rm\Sigma})$ of almost-strict difference rings is benign if for some (or equivalently, for all)  ${\it\sigma}\in {\rm\Sigma}$, the morphism
${\it\sigma}\in {\rm\Sigma}$, the morphism  $(S,{\it\sigma}^{{\it\psi}})\rightarrow (R,{\it\sigma})$ is benign.
$(S,{\it\sigma}^{{\it\psi}})\rightarrow (R,{\it\sigma})$ is benign.(2) A morphism
 $(X,{\rm\Sigma})\rightarrow (Y,T)$ of almost-strict difference schemes is benign if it is affine and above each open affine subset of
$(X,{\rm\Sigma})\rightarrow (Y,T)$ of almost-strict difference schemes is benign if it is affine and above each open affine subset of  $Y$ it is modeled by a fixed-point spectrum of a benign morphism of rings.
$Y$ it is modeled by a fixed-point spectrum of a benign morphism of rings.(3) In the situation of (2), the morphism is proper benign, if the relevant difference ring extensions are proper benign.
An immediate consequence of 5.7 is the following.
Lemma 5.9. Let 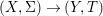 $(X,{\rm\Sigma})\rightarrow (Y,T)$ be a proper benign Galois morphism. For any
$(X,{\rm\Sigma})\rightarrow (Y,T)$ be a proper benign Galois morphism. For any ![]() ${\it\tau}\in T$ and
${\it\tau}\in T$ and ![]() ${\it\sigma}\in {\rm\Sigma}$ mapping to
${\it\sigma}\in {\rm\Sigma}$ mapping to ![]() ${\it\tau}$, any
${\it\tau}$, any ![]() $y\in Y^{{\it\tau}}$, any algebraically closed difference field
$y\in Y^{{\it\tau}}$, any algebraically closed difference field ![]() $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending 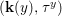 $(\mathbf{k}(y),{\it\tau}^{y})$, any
$(\mathbf{k}(y),{\it\tau}^{y})$, any 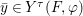 $\bar{y}\in Y^{{\it\tau}}(F,{\it\varphi})$ above
$\bar{y}\in Y^{{\it\tau}}(F,{\it\varphi})$ above ![]() $y$, there exists an
$y$, there exists an 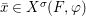 $\bar{x}\in X^{{\it\sigma}}(F,{\it\varphi})$ lifting
$\bar{x}\in X^{{\it\sigma}}(F,{\it\varphi})$ lifting ![]() $\bar{y}$.
$\bar{y}$.
Definition 5.10. Two difference schemes 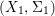 $(X_{1},{\rm\Sigma}_{1})$ and
$(X_{1},{\rm\Sigma}_{1})$ and 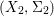 $(X_{2},{\rm\Sigma}_{2})$ are called equivalent, written
$(X_{2},{\rm\Sigma}_{2})$ are called equivalent, written 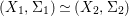 $(X_{1},{\rm\Sigma}_{1})\simeq (X_{2},{\rm\Sigma}_{2})$, if they have isomorphic inversive closures,
$(X_{1},{\rm\Sigma}_{1})\simeq (X_{2},{\rm\Sigma}_{2})$, if they have isomorphic inversive closures, 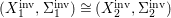 $(X_{1}^{\text{inv}},{\rm\Sigma}_{1}^{\text{inv}})\cong (X_{2}^{\text{inv}},{\rm\Sigma}_{2}^{\text{inv}})$.
$(X_{1}^{\text{inv}},{\rm\Sigma}_{1}^{\text{inv}})\cong (X_{2}^{\text{inv}},{\rm\Sigma}_{2}^{\text{inv}})$.
The following is a slight refinement of a fundamental theorem from [Reference Babbitt3], showing how to use it for not necessarily inversive difference fields.
Lemma 5.11. (Babbitt’s Theorem)
Let 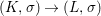 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a separable
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a separable ![]() ${\it\sigma}$-separable quasi-Galois extension of finite
${\it\sigma}$-separable quasi-Galois extension of finite ![]() ${\it\sigma}$-type. Then we have a tower
${\it\sigma}$-type. Then we have a tower
 $$\begin{eqnarray}(K,{\it\sigma})\rightarrow (L_{0},{\it\sigma})\rightarrow (L_{1},{\it\sigma})\rightarrow \cdots \rightarrow (L_{n},{\it\sigma})\simeq (L,{\it\sigma})\end{eqnarray}$$
$$\begin{eqnarray}(K,{\it\sigma})\rightarrow (L_{0},{\it\sigma})\rightarrow (L_{1},{\it\sigma})\rightarrow \cdots \rightarrow (L_{n},{\it\sigma})\simeq (L,{\it\sigma})\end{eqnarray}$$ of difference field extensions with ![]() $L_{0}/K$ finite and all
$L_{0}/K$ finite and all  $L_{i+1}/L_{i}$ benign for
$L_{i+1}/L_{i}$ benign for ![]() $i\geqslant 0$.
$i\geqslant 0$.
Proof. Let us remark that, if ![]() $F/K$ is
$F/K$ is ![]() ${\it\sigma}$-separable, and
${\it\sigma}$-separable, and  $F^{\text{inv}}=K^{\text{inv}}(a)_{{\it\sigma}}$ for some
$F^{\text{inv}}=K^{\text{inv}}(a)_{{\it\sigma}}$ for some 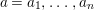 $a=a_{1},\ldots ,a_{n}$, then there is an
$a=a_{1},\ldots ,a_{n}$, then there is an ![]() $r\geqslant 0$ such that
$r\geqslant 0$ such that 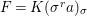 $F=K({\it\sigma}^{r}a)_{{\it\sigma}}$.
$F=K({\it\sigma}^{r}a)_{{\it\sigma}}$.
The original theorem from [Reference Babbitt3] gives that, writing 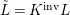 $\tilde{L}=K^{\text{inv}}L$, and
$\tilde{L}=K^{\text{inv}}L$, and ![]() $\tilde{L}_{0}$ for the core of
$\tilde{L}_{0}$ for the core of ![]() $K^{\text{inv}}$ in
$K^{\text{inv}}$ in ![]() $\tilde{L}$, there exist
$\tilde{L}$, there exist 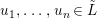 $u_{1},\ldots ,u_{n}\in \tilde{L}$ such that
$u_{1},\ldots ,u_{n}\in \tilde{L}$ such that 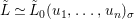 $\tilde{L}\simeq \tilde{L}_{0}(u_{1},\ldots ,u_{n})_{{\it\sigma}}$ and for every
$\tilde{L}\simeq \tilde{L}_{0}(u_{1},\ldots ,u_{n})_{{\it\sigma}}$ and for every  $0\leqslant i\leqslant n-1$,
$0\leqslant i\leqslant n-1$,  $\tilde{L}_{0}(u_{1},\ldots ,u_{i+1})_{{\it\sigma}}$ is a benign extension of
$\tilde{L}_{0}(u_{1},\ldots ,u_{i+1})_{{\it\sigma}}$ is a benign extension of  $\tilde{L}_{0}(u_{1},\ldots ,u_{i})_{{\it\sigma}}$ with normal minimal generator
$\tilde{L}_{0}(u_{1},\ldots ,u_{i})_{{\it\sigma}}$ with normal minimal generator ![]() $u_{i+1}$.
$u_{i+1}$.
It is known that ![]() $\tilde{L}_{0}$ is inversive, so using the above remark for
$\tilde{L}_{0}$ is inversive, so using the above remark for ![]() $F=\tilde{L}_{0}$, we deduce that
$F=\tilde{L}_{0}$, we deduce that 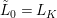 $\tilde{L}_{0}=L_{K}$, the core of
$\tilde{L}_{0}=L_{K}$, the core of ![]() $K$ in
$K$ in ![]() $L$. Bearing in mind that
$L$. Bearing in mind that ![]() $L\simeq \tilde{L}$, we produce the required decomposition.◻
$L\simeq \tilde{L}$, we produce the required decomposition.◻
Babbitt’s theorem on algebraic extensions of difference fields has the following consequence in our terminology, providing a deep structure theorem.
Theorem 5.12. (Babbitt’s decomposition)
Any generically étale quasi-Galois ![]() ${\it\sigma}$-separable morphism of finite transformal type
${\it\sigma}$-separable morphism of finite transformal type 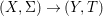 $(X,{\rm\Sigma})\rightarrow (Y,T)$ of transformally integral normal affine almost-strict difference schemes factorizes as
$(X,{\rm\Sigma})\rightarrow (Y,T)$ of transformally integral normal affine almost-strict difference schemes factorizes as
 $$\begin{eqnarray}(X,{\rm\Sigma})\simeq (X_{n},{\rm\Sigma}_{n})\rightarrow \cdots \rightarrow (X_{1},{\rm\Sigma}_{1})\rightarrow (X_{0},{\rm\Sigma}_{0})\rightarrow (Y,T),\end{eqnarray}$$
$$\begin{eqnarray}(X,{\rm\Sigma})\simeq (X_{n},{\rm\Sigma}_{n})\rightarrow \cdots \rightarrow (X_{1},{\rm\Sigma}_{1})\rightarrow (X_{0},{\rm\Sigma}_{0})\rightarrow (Y,T),\end{eqnarray}$$ where  $(X_{0},{\rm\Sigma}_{0})\rightarrow (Y,T)$ is generically finite étale quasi-Galois and for
$(X_{0},{\rm\Sigma}_{0})\rightarrow (Y,T)$ is generically finite étale quasi-Galois and for ![]() $i\geqslant 0$,
$i\geqslant 0$, 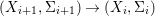 $(X_{i+1},{\rm\Sigma}_{i+1})\rightarrow (X_{i},{\rm\Sigma}_{i})$ is benign Galois. Modulo a transformal localization of
$(X_{i+1},{\rm\Sigma}_{i+1})\rightarrow (X_{i},{\rm\Sigma}_{i})$ is benign Galois. Modulo a transformal localization of ![]() $Y$, we can achieve that
$Y$, we can achieve that 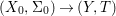 $(X_{0},{\rm\Sigma}_{0})\rightarrow (Y,T)$ is finite étale quasi-Galois, and that
$(X_{0},{\rm\Sigma}_{0})\rightarrow (Y,T)$ is finite étale quasi-Galois, and that 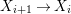 $X_{i+1}\rightarrow X_{i}$ are étale proper benign Galois.
$X_{i+1}\rightarrow X_{i}$ are étale proper benign Galois.
Proof. By applying Babbitt’s theorem 5.11 to the extension of difference function fields 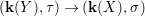 $(\mathbf{k}(Y),{\it\tau})\rightarrow (\mathbf{k}(X),{\it\sigma})$ for a suitable choice of
$(\mathbf{k}(Y),{\it\tau})\rightarrow (\mathbf{k}(X),{\it\sigma})$ for a suitable choice of ![]() ${\it\sigma}$ and
${\it\sigma}$ and ![]() ${\it\tau}$ we obtain a tower of difference field extensions
${\it\tau}$ we obtain a tower of difference field extensions
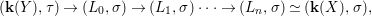 $$\begin{eqnarray}(\mathbf{k}(Y),{\it\tau})\rightarrow (L_{0},{\it\sigma})\rightarrow (L_{1},{\it\sigma})\cdots \rightarrow (L_{n},{\it\sigma})\simeq (\mathbf{k}(X),{\it\sigma}),\end{eqnarray}$$
$$\begin{eqnarray}(\mathbf{k}(Y),{\it\tau})\rightarrow (L_{0},{\it\sigma})\rightarrow (L_{1},{\it\sigma})\cdots \rightarrow (L_{n},{\it\sigma})\simeq (\mathbf{k}(X),{\it\sigma}),\end{eqnarray}$$ where 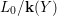 $L_{0}/\mathbf{k}(Y)$ is finite and each
$L_{0}/\mathbf{k}(Y)$ is finite and each 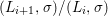 $(L_{i+1},{\it\sigma})/(L_{i},{\it\sigma})$ is benign for
$(L_{i+1},{\it\sigma})/(L_{i},{\it\sigma})$ is benign for ![]() $i\geqslant 0$. We let
$i\geqslant 0$. We let ![]() ${\rm\Sigma}_{i}$ be the
${\rm\Sigma}_{i}$ be the ![]() $\mathit{Diff}$-structure obtained as a restriction of
$\mathit{Diff}$-structure obtained as a restriction of ![]() ${\rm\Sigma}$ from
${\rm\Sigma}$ from ![]() $L_{n}$ to
$L_{n}$ to ![]() $L_{i}$. Let
$L_{i}$. Let 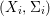 $(X_{i},{\rm\Sigma}_{i})$ be the normalization of
$(X_{i},{\rm\Sigma}_{i})$ be the normalization of ![]() $(Y,T)$ in
$(Y,T)$ in ![]() $(L_{i},{\rm\Sigma}_{i})$. It is clear from [Reference Tomašić24, 2.56] that by a transformal localization we can achieve that
$(L_{i},{\rm\Sigma}_{i})$. It is clear from [Reference Tomašić24, 2.56] that by a transformal localization we can achieve that 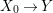 $X_{0}\rightarrow Y$ is finite étale and it remains to show that each
$X_{0}\rightarrow Y$ is finite étale and it remains to show that each 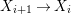 $X_{i+1}\rightarrow X_{i}$ can be made étale benign, which is granted by the following lemma.◻
$X_{i+1}\rightarrow X_{i}$ can be made étale benign, which is granted by the following lemma.◻
Lemma 5.13. Let ![]() $(R,{\it\sigma})$ be a normal transformal domain with fraction field
$(R,{\it\sigma})$ be a normal transformal domain with fraction field ![]() $(K,{\it\sigma})$ and let
$(K,{\it\sigma})$ and let 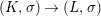 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a benign extension of difference fields such that
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a benign extension of difference fields such that ![]() $L$ is the composite of the linearly disjoint subfields
$L$ is the composite of the linearly disjoint subfields 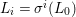 $L_{i}={\it\sigma}^{i}(L_{0})$ where
$L_{i}={\it\sigma}^{i}(L_{0})$ where ![]() $L_{0}$ is a fraction field of an étale
$L_{0}$ is a fraction field of an étale ![]() $R$-algebra
$R$-algebra ![]() $A_{0}$. Then the normalization of
$A_{0}$. Then the normalization of ![]() $R$ in
$R$ in ![]() $L$ is the (limit) tensor product of the
$L$ is the (limit) tensor product of the ![]() $A_{0{\it\sigma}^{i}}$ over
$A_{0{\it\sigma}^{i}}$ over ![]() $R$ and thus benign over
$R$ and thus benign over ![]() $R$.
$R$.
Proof. Since ![]() $A_{0}$ is étale over
$A_{0}$ is étale over ![]() $R$ so is any
$R$ so is any ![]() $A_{0{\it\sigma}^{i}}$, and any tensor product of those is therefore
$A_{0{\it\sigma}^{i}}$, and any tensor product of those is therefore ![]() $R$-torsion-free and the conclusion follows from linear disjointness in the spirit of the proof of 3.3.◻
$R$-torsion-free and the conclusion follows from linear disjointness in the spirit of the proof of 3.3.◻
5.3 Galois closure
Lemma 5.14. Let 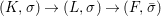 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})\rightarrow (F,\bar{{\it\sigma}})$ be a tower of difference field extensions with
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})\rightarrow (F,\bar{{\it\sigma}})$ be a tower of difference field extensions with ![]() $L/K$ algebraic, and suppose that the quasi-Galois (normal) closure
$L/K$ algebraic, and suppose that the quasi-Galois (normal) closure ![]() $\tilde{L}$ of
$\tilde{L}$ of ![]() $L$ over
$L$ over ![]() $K$ is contained in
$K$ is contained in ![]() $F$. Then
$F$. Then 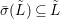 $\bar{{\it\sigma}}(\tilde{L})\subseteq \tilde{L}$ and
$\bar{{\it\sigma}}(\tilde{L})\subseteq \tilde{L}$ and ![]() $(\tilde{L},\tilde{{\it\sigma}})$ is a difference field extension of
$(\tilde{L},\tilde{{\it\sigma}})$ is a difference field extension of ![]() $(L,{\it\sigma})$, where
$(L,{\it\sigma})$, where 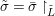 $\tilde{{\it\sigma}}=\bar{{\it\sigma}}\restriction_{\tilde{L}}$.
$\tilde{{\it\sigma}}=\bar{{\it\sigma}}\restriction_{\tilde{L}}$.
Proof. If ![]() ${\it\alpha}\in \tilde{L}$, then it is a conjugate of some
${\it\alpha}\in \tilde{L}$, then it is a conjugate of some ![]() ${\it\alpha}_{0}\in L$. In other words, the minimal polynomial
${\it\alpha}_{0}\in L$. In other words, the minimal polynomial 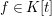 $f\in K[t]$ of
$f\in K[t]$ of ![]() ${\it\alpha}_{0}$ over
${\it\alpha}_{0}$ over ![]() $K$ splits as
$K$ splits as 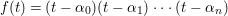 $f(t)=(t-{\it\alpha}_{0})(t-{\it\alpha}_{1})\cdots (t-{\it\alpha}_{n})$, for
$f(t)=(t-{\it\alpha}_{0})(t-{\it\alpha}_{1})\cdots (t-{\it\alpha}_{n})$, for ![]() ${\it\alpha}_{i}\in \tilde{L}$, and
${\it\alpha}_{i}\in \tilde{L}$, and ![]() ${\it\alpha}$ is one of the
${\it\alpha}$ is one of the ![]() ${\it\alpha}_{i}$. Then
${\it\alpha}_{i}$. Then 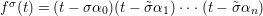 $f^{{\it\sigma}}(t)=(t-{\it\sigma}{\it\alpha}_{0})(t-\tilde{{\it\sigma}}{\it\alpha}_{1})\cdots (t-\tilde{{\it\sigma}}{\it\alpha}_{n})$ is the minimal polynomial of
$f^{{\it\sigma}}(t)=(t-{\it\sigma}{\it\alpha}_{0})(t-\tilde{{\it\sigma}}{\it\alpha}_{1})\cdots (t-\tilde{{\it\sigma}}{\it\alpha}_{n})$ is the minimal polynomial of ![]() ${\it\sigma}{\it\alpha}_{0}$, which is again in
${\it\sigma}{\it\alpha}_{0}$, which is again in ![]() $L$, so
$L$, so ![]() $\tilde{{\it\alpha}}_{i}$ are its conjugates and therefore they lie in
$\tilde{{\it\alpha}}_{i}$ are its conjugates and therefore they lie in ![]() $\tilde{L}$.◻
$\tilde{L}$.◻
Remark 5.15. Cohn remarks in [Reference Cohn7, Chapter 7, no. 16] that the algebraic closure ![]() $\bar{L}$ of
$\bar{L}$ of ![]() $L$ can always be equipped with an endomorphism
$L$ can always be equipped with an endomorphism ![]() $\tilde{{\it\sigma}}$ so that
$\tilde{{\it\sigma}}$ so that ![]() $(\bar{L},\tilde{{\it\sigma}})$ extends
$(\bar{L},\tilde{{\it\sigma}})$ extends ![]() $(L,{\it\sigma})$. Thus (considering
$(L,{\it\sigma})$. Thus (considering ![]() $(\bar{L},\bar{{\it\sigma}})$ in the role of
$(\bar{L},\bar{{\it\sigma}})$ in the role of ![]() $(F,\bar{{\it\sigma}})$ above), the quasi-Galois closure
$(F,\bar{{\it\sigma}})$ above), the quasi-Galois closure ![]() $\tilde{L}$ can always be made (noncanonically) into a difference field extension of
$\tilde{L}$ can always be made (noncanonically) into a difference field extension of ![]() $(L,{\it\sigma})$.
$(L,{\it\sigma})$.
Definition 5.16. Suppose ![]() $(L,{\it\sigma})$ is a separable extension of
$(L,{\it\sigma})$ is a separable extension of ![]() $(K,{\it\sigma})$, and let
$(K,{\it\sigma})$, and let ![]() $(\tilde{L},\tilde{{\it\sigma}})$ be a choice of a difference structure on the quasi-Galois closure of
$(\tilde{L},\tilde{{\it\sigma}})$ be a choice of a difference structure on the quasi-Galois closure of ![]() $L$ over
$L$ over ![]() $K$. The diagram
$K$. The diagram
is called the Galois closure of ![]() $(L,{\it\sigma})$ over
$(L,{\it\sigma})$ over ![]() $(K,{\it\sigma})$, where
$(K,{\it\sigma})$, where ![]() ${\rm\Sigma}$ is the set of all lifts of
${\rm\Sigma}$ is the set of all lifts of ![]() ${\it\sigma}$ from
${\it\sigma}$ from ![]() $K$ to
$K$ to ![]() $\tilde{L}$, and
$\tilde{L}$, and ![]() $\mathring{\Sigma}\subseteq {\rm\Sigma}$ is the set of all lifts of
$\mathring{\Sigma}\subseteq {\rm\Sigma}$ is the set of all lifts of ![]() ${\it\sigma}$ from
${\it\sigma}$ from ![]() $L$ to
$L$ to ![]() $\tilde{L}$. In fact,
$\tilde{L}$. In fact, 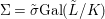 ${\rm\Sigma}=\tilde{{\it\sigma}}\text{Gal}(\tilde{L}/K)$, and
${\rm\Sigma}=\tilde{{\it\sigma}}\text{Gal}(\tilde{L}/K)$, and 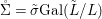 $\mathring{\Sigma}=\tilde{{\it\sigma}}\text{Gal}(\tilde{L}/L)$.
$\mathring{\Sigma}=\tilde{{\it\sigma}}\text{Gal}(\tilde{L}/L)$.
Proposition 5.17. (The universal property of Galois closure)
Let ![]() $(L,{\it\sigma})$ be a separable extension of
$(L,{\it\sigma})$ be a separable extension of ![]() $(K,{\it\sigma})$, and suppose
$(K,{\it\sigma})$, and suppose ![]() $(F,{\rm\Sigma}_{F})$ is Galois over
$(F,{\rm\Sigma}_{F})$ is Galois over ![]() $(K,{\it\sigma})$ such that there is a
$(K,{\it\sigma})$ such that there is a ![]() $\bar{{\it\sigma}}\in {\rm\Sigma}_{F}$ with
$\bar{{\it\sigma}}\in {\rm\Sigma}_{F}$ with ![]() $(F,\bar{{\it\sigma}})$ extending
$(F,\bar{{\it\sigma}})$ extending ![]() $(L,{\it\sigma})$. Then there are extensions
$(L,{\it\sigma})$. Then there are extensions 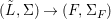 $(\tilde{L},{\rm\Sigma})\rightarrow (F,{\rm\Sigma}_{F})$ and
$(\tilde{L},{\rm\Sigma})\rightarrow (F,{\rm\Sigma}_{F})$ and 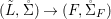 $(\tilde{L},\mathring{\Sigma})\rightarrow (F,\mathring{\Sigma}_{F})$, where
$(\tilde{L},\mathring{\Sigma})\rightarrow (F,\mathring{\Sigma}_{F})$, where 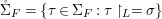 $\mathring{\Sigma}_{F}=\{{\it\tau}\in {\rm\Sigma}_{F}:{\it\tau}\restriction_{L}={\it\sigma}\}$.
$\mathring{\Sigma}_{F}=\{{\it\tau}\in {\rm\Sigma}_{F}:{\it\tau}\restriction_{L}={\it\sigma}\}$.
Proof. By the universal property of (algebraic) Galois closure, ![]() $\tilde{L}\subseteq F$ and
$\tilde{L}\subseteq F$ and ![]() $F/\tilde{L}$ is Galois. Let
$F/\tilde{L}$ is Galois. Let ![]() $\bar{{\it\sigma}}\in {\rm\Sigma}_{F}$ be an endomorphism such that
$\bar{{\it\sigma}}\in {\rm\Sigma}_{F}$ be an endomorphism such that 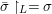 $\bar{{\it\sigma}}\restriction_{L}={\it\sigma}$. By 5.14,
$\bar{{\it\sigma}}\restriction_{L}={\it\sigma}$. By 5.14, 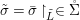 $\tilde{{\it\sigma}}=\bar{{\it\sigma}}\restriction_{\tilde{L}}\in \mathring{\Sigma}$, and we know that
$\tilde{{\it\sigma}}=\bar{{\it\sigma}}\restriction_{\tilde{L}}\in \mathring{\Sigma}$, and we know that 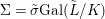 ${\rm\Sigma}=\tilde{{\it\sigma}}\text{Gal}(\tilde{L}/K)$,
${\rm\Sigma}=\tilde{{\it\sigma}}\text{Gal}(\tilde{L}/K)$, 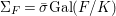 ${\rm\Sigma}_{F}=\bar{{\it\sigma}}\text{Gal}(F/K)$ and that
${\rm\Sigma}_{F}=\bar{{\it\sigma}}\text{Gal}(F/K)$ and that
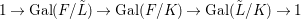 $$\begin{eqnarray}1\rightarrow \text{Gal}(F/\tilde{L})\rightarrow \text{Gal}(F/K)\rightarrow \text{Gal}(\tilde{L}/K)\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \text{Gal}(F/\tilde{L})\rightarrow \text{Gal}(F/K)\rightarrow \text{Gal}(\tilde{L}/K)\rightarrow 1\end{eqnarray}$$ is exact, so the restriction map 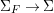 ${\rm\Sigma}_{F}\rightarrow {\rm\Sigma}$ is onto, giving the inclusion
${\rm\Sigma}_{F}\rightarrow {\rm\Sigma}$ is onto, giving the inclusion 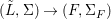 $(\tilde{L},{\rm\Sigma})\rightarrow (F,{\rm\Sigma}_{F})$. Similarly we get the inclusion
$(\tilde{L},{\rm\Sigma})\rightarrow (F,{\rm\Sigma}_{F})$. Similarly we get the inclusion 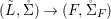 $(\tilde{L},\mathring{\Sigma})\rightarrow (F,\mathring{\Sigma}_{F})$.◻
$(\tilde{L},\mathring{\Sigma})\rightarrow (F,\mathring{\Sigma}_{F})$.◻
Definition 5.18. Let 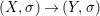 $(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a generically étale
$(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a generically étale ![]() ${\it\sigma}$-separable finite morphism of transformally integral normal difference schemes, and denote by
${\it\sigma}$-separable finite morphism of transformally integral normal difference schemes, and denote by 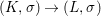 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ the corresponding extension of function fields, let
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ the corresponding extension of function fields, let ![]() $(\tilde{L},{\rm\Sigma})$ and
$(\tilde{L},{\rm\Sigma})$ and ![]() $\mathring{\Sigma}$ be as in 5.16 (
$\mathring{\Sigma}$ be as in 5.16 (![]() ${\rm\Sigma}$ is finite in this case), and write
${\rm\Sigma}$ is finite in this case), and write 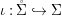 ${\it\iota}:\mathring{\Sigma}{\hookrightarrow}{\rm\Sigma}$. Let
${\it\iota}:\mathring{\Sigma}{\hookrightarrow}{\rm\Sigma}$. Let ![]() $(\tilde{X},{\rm\Sigma})$ be the normalization of
$(\tilde{X},{\rm\Sigma})$ be the normalization of ![]() $Y$ in
$Y$ in ![]() $(\tilde{L},{\rm\Sigma})$, and let
$(\tilde{L},{\rm\Sigma})$, and let 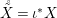 $\mathring{\tilde{X}}={\it\iota}^{\ast }X$. The Galois closure of
$\mathring{\tilde{X}}={\it\iota}^{\ast }X$. The Galois closure of ![]() $X$ over
$X$ over ![]() $Y$ is the resulting diagram
$Y$ is the resulting diagram
in which the vertical arrows are Galois covers.
5.4 Ampleness of finite difference structures
A geometric motivation for the study of generalized difference geometry was the quest for a framework that gives rise to a suitable notion of a Galois cover. Intuitively, a morphism 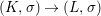 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of difference fields with
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of difference fields with ![]() $K\rightarrow L$ Galois is not a Galois extension in the category of difference rings. Instead, one should consider the extension
$K\rightarrow L$ Galois is not a Galois extension in the category of difference rings. Instead, one should consider the extension 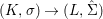 $(K,{\it\sigma})\rightarrow (L,\hat{{\rm\Sigma}})$ where
$(K,{\it\sigma})\rightarrow (L,\hat{{\rm\Sigma}})$ where ![]() $\hat{{\rm\Sigma}}$ is the set of all lifts of
$\hat{{\rm\Sigma}}$ is the set of all lifts of ![]() ${\it\sigma}$ to
${\it\sigma}$ to ![]() $L$. Even in the common case where
$L$. Even in the common case where ![]() $L$ is algebraic of finite
$L$ is algebraic of finite ![]() ${\it\sigma}$-type over
${\it\sigma}$-type over ![]() $K$, this typically involves a consideration of a profinite structure
$K$, this typically involves a consideration of a profinite structure ![]() $\hat{{\rm\Sigma}}$. This certainly works, but falls beyond the scope of the present paper.
$\hat{{\rm\Sigma}}$. This certainly works, but falls beyond the scope of the present paper.
The aim of the following string of results is to show that, for most purposes in difference algebraic geometry, it suffices to consider difference rings and fields (and schemes) with finite difference structures.
Lemma 5.19. Let  $(L_{0},{\it\sigma})\rightarrow (L,{\it\sigma})$ be a coreless extension of an inversive difference field
$(L_{0},{\it\sigma})\rightarrow (L,{\it\sigma})$ be a coreless extension of an inversive difference field ![]() $L_{0}$ (i.e., the core of
$L_{0}$ (i.e., the core of ![]() $L_{0}$ in
$L_{0}$ in ![]() $L$ is
$L$ is ![]() $L_{0}$). Then
$L_{0}$). Then
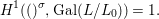 $$\begin{eqnarray}H^{1}(()^{{\it\sigma}},\text{Gal}(L/L_{0}))=1.\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(()^{{\it\sigma}},\text{Gal}(L/L_{0}))=1.\end{eqnarray}$$Proof. Using Babbitt’s decomposition, let
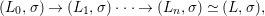 $$\begin{eqnarray}(L_{0},{\it\sigma})\rightarrow (L_{1},{\it\sigma})\cdots \rightarrow (L_{n},{\it\sigma})\simeq (L,{\it\sigma}),\end{eqnarray}$$
$$\begin{eqnarray}(L_{0},{\it\sigma})\rightarrow (L_{1},{\it\sigma})\cdots \rightarrow (L_{n},{\it\sigma})\simeq (L,{\it\sigma}),\end{eqnarray}$$ be a tower of benign difference field extensions. By 5.6, 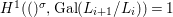 $H^{1}(()^{{\it\sigma}},\text{Gal}(L_{i+1}/L_{i}))=1$ for all
$H^{1}(()^{{\it\sigma}},\text{Gal}(L_{i+1}/L_{i}))=1$ for all ![]() $i\geqslant 0$. It is straightforward now to prove that
$i\geqslant 0$. It is straightforward now to prove that 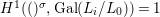 $H^{1}(()^{{\it\sigma}},\text{Gal}(L_{i}/L_{0}))=1$ by induction, using the long exact sequence for difference cohomology associated with the short exact sequence
$H^{1}(()^{{\it\sigma}},\text{Gal}(L_{i}/L_{0}))=1$ by induction, using the long exact sequence for difference cohomology associated with the short exact sequence
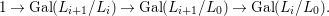 $$\begin{eqnarray}1\rightarrow \text{Gal}(L_{i+1}/L_{i})\rightarrow \text{Gal}(L_{i+1}/L_{0})\rightarrow \text{Gal}(L_{i}/L_{0}).\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \text{Gal}(L_{i+1}/L_{i})\rightarrow \text{Gal}(L_{i+1}/L_{0})\rightarrow \text{Gal}(L_{i}/L_{0}).\end{eqnarray}$$ In particular, we have that 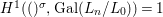 $H^{1}(()^{{\it\sigma}},\text{Gal}(L_{n}/L_{0}))=1$. By analogous considerations, we obtain
$H^{1}(()^{{\it\sigma}},\text{Gal}(L_{n}/L_{0}))=1$. By analogous considerations, we obtain 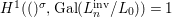 $H^{1}(()^{{\it\sigma}},\text{Gal}(L_{n}^{\text{inv}}/L_{0}))=1$.
$H^{1}(()^{{\it\sigma}},\text{Gal}(L_{n}^{\text{inv}}/L_{0}))=1$.
If 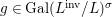 $g\in \text{Gal}(L^{\text{inv}}/L)^{{\it\sigma}}$, then also
$g\in \text{Gal}(L^{\text{inv}}/L)^{{\it\sigma}}$, then also ![]() $g^{{\it\sigma}^{r}}=g$ for every
$g^{{\it\sigma}^{r}}=g$ for every ![]() $r$. For
$r$. For 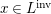 $x\in L^{\text{inv}}$, choose
$x\in L^{\text{inv}}$, choose ![]() $r$ so that
$r$ so that 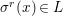 ${\it\sigma}^{r}(x)\in L$, and then
${\it\sigma}^{r}(x)\in L$, and then 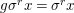 $g{\it\sigma}^{r}x={\it\sigma}^{r}x$, so
$g{\it\sigma}^{r}x={\it\sigma}^{r}x$, so 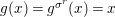 $g(x)=g^{{\it\sigma}^{r}}(x)=x$, and thus
$g(x)=g^{{\it\sigma}^{r}}(x)=x$, and thus ![]() $g$ is the identity. We conclude that
$g$ is the identity. We conclude that 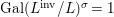 $\text{Gal}(L^{\text{inv}}/L)^{{\it\sigma}}=1$.
$\text{Gal}(L^{\text{inv}}/L)^{{\it\sigma}}=1$.
Using the fact that 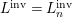 $L^{\text{inv}}=L_{n}^{\text{inv}}$, the cohomology long exact sequence (extended by 5.3) associated with
$L^{\text{inv}}=L_{n}^{\text{inv}}$, the cohomology long exact sequence (extended by 5.3) associated with
 $$\begin{eqnarray}1\rightarrow \text{Gal}(L^{\text{inv}}/L)\rightarrow \text{Gal}(L^{\text{inv}}/L_{0})\rightarrow \text{Gal}(L/L_{0})\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \text{Gal}(L^{\text{inv}}/L)\rightarrow \text{Gal}(L^{\text{inv}}/L_{0})\rightarrow \text{Gal}(L/L_{0})\rightarrow 1\end{eqnarray}$$becomes
 $$\begin{eqnarray}\displaystyle & 1\rightarrow 1\rightarrow \text{Gal}(L_{1}^{\text{inv}}/L_{0})^{{\it\sigma}}\rightarrow \text{Gal}(L/L_{0})^{{\it\sigma}}\rightarrow & \displaystyle \nonumber\\ \displaystyle & \rightarrow H^{1}(()^{{\it\sigma}},L^{\text{inv}}/L)\rightarrow 1\rightarrow H^{1}(()^{{\it\sigma}},L/L_{0})\rightarrow 1, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & 1\rightarrow 1\rightarrow \text{Gal}(L_{1}^{\text{inv}}/L_{0})^{{\it\sigma}}\rightarrow \text{Gal}(L/L_{0})^{{\it\sigma}}\rightarrow & \displaystyle \nonumber\\ \displaystyle & \rightarrow H^{1}(()^{{\it\sigma}},L^{\text{inv}}/L)\rightarrow 1\rightarrow H^{1}(()^{{\it\sigma}},L/L_{0})\rightarrow 1, & \displaystyle \nonumber\end{eqnarray}$$ whence we conclude that 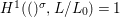 $H^{1}(()^{{\it\sigma}},L/L_{0})=1$, and, since
$H^{1}(()^{{\it\sigma}},L/L_{0})=1$, and, since 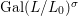 $\text{Gal}(L/L_{0})^{{\it\sigma}}$ is finite as a
$\text{Gal}(L/L_{0})^{{\it\sigma}}$ is finite as a ![]() ${\it\sigma}$-Galois group of an algebraic extension of finite
${\it\sigma}$-Galois group of an algebraic extension of finite ![]() ${\it\sigma}$-type, that all the remaining terms are finite.◻
${\it\sigma}$-type, that all the remaining terms are finite.◻
Lemma 5.20. Let 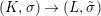 $(K,{\it\sigma})\rightarrow (L,\tilde{{\it\sigma}})$ be a separable
$(K,{\it\sigma})\rightarrow (L,\tilde{{\it\sigma}})$ be a separable ![]() ${\it\sigma}$-separable quasi-Galois extension of finite
${\it\sigma}$-separable quasi-Galois extension of finite ![]() $\tilde{{\it\sigma}}$-type. Let
$\tilde{{\it\sigma}}$-type. Let  $L_{0}=L_{K}$ be the core of
$L_{0}=L_{K}$ be the core of ![]() $K$ in
$K$ in ![]() $L$. The exact sequence
$L$. The exact sequence
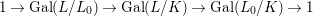 $$\begin{eqnarray}1\rightarrow \text{Gal}(L/L_{0})\rightarrow \text{Gal}(L/K)\rightarrow \text{Gal}(L_{0}/K)\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \text{Gal}(L/L_{0})\rightarrow \text{Gal}(L/K)\rightarrow \text{Gal}(L_{0}/K)\rightarrow 1\end{eqnarray}$$ is nearly split in the sense that there exists a finite ![]() $()^{{\it\sigma}}$-invariant subgroup
$()^{{\it\sigma}}$-invariant subgroup ![]() $G_{1}$ of
$G_{1}$ of 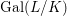 $\text{Gal}(L/K)$ which maps onto
$\text{Gal}(L/K)$ which maps onto 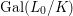 $\text{Gal}(L_{0}/K)$.
$\text{Gal}(L_{0}/K)$.
Moreover, the set of isomorphism classes of all lifts of ![]() ${\it\sigma}$ from
${\it\sigma}$ from ![]() $K$ to
$K$ to ![]() $L$ is in one-to-one correspondence with the set of isomorphism classes of lifts of
$L$ is in one-to-one correspondence with the set of isomorphism classes of lifts of ![]() ${\it\sigma}$ from
${\it\sigma}$ from ![]() $K$ to
$K$ to ![]() $L_{0}$ and
$L_{0}$ and ![]() $G_{1}$ can be chosen so that
$G_{1}$ can be chosen so that ![]() ${\it\sigma}G_{1}$ contains a set of representatives for those isomorphism classes.
${\it\sigma}G_{1}$ contains a set of representatives for those isomorphism classes.
Proof. The assumption that ![]() $L$ is
$L$ is ![]() ${\it\sigma}$-separable allows us to assume that
${\it\sigma}$-separable allows us to assume that ![]() $K$ is inversive, and then
$K$ is inversive, and then ![]() $L_{0}$ is inversive by [Reference Cohn7, Chapter 7, no. 15]. Let us introduce the shorthand notation
$L_{0}$ is inversive by [Reference Cohn7, Chapter 7, no. 15]. Let us introduce the shorthand notation 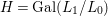 $H=\text{Gal}(L_{1}/L_{0})$,
$H=\text{Gal}(L_{1}/L_{0})$, 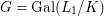 $G=\text{Gal}(L_{1}/K)$,
$G=\text{Gal}(L_{1}/K)$, 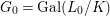 $G_{0}=\text{Gal}(L_{0}/K)$, and let us denote by
$G_{0}=\text{Gal}(L_{0}/K)$, and let us denote by ![]() ${\rm\Phi}$ the operator
${\rm\Phi}$ the operator  $()^{{\it\sigma}^{n}}:G\rightarrow G$, where
$()^{{\it\sigma}^{n}}:G\rightarrow G$, where ![]() $n$ is the order of
$n$ is the order of ![]() $()^{{\it\sigma}}$ on
$()^{{\it\sigma}}$ on ![]() $G_{0}$.
$G_{0}$.
Using 5.19, we get that  $H^{1}(()^{{\it\sigma}},H)=1$ and
$H^{1}(()^{{\it\sigma}},H)=1$ and 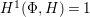 $H^{1}({\rm\Phi},H)=1$ so the long exact sequences (from 5.3) for (nonabelian) difference cohomology become
$H^{1}({\rm\Phi},H)=1$ so the long exact sequences (from 5.3) for (nonabelian) difference cohomology become
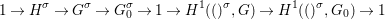 $$\begin{eqnarray}1\rightarrow H^{{\it\sigma}}\rightarrow G^{{\it\sigma}}\rightarrow G_{0}^{{\it\sigma}}\rightarrow 1\rightarrow H^{1}(()^{{\it\sigma}},G)\rightarrow H^{1}(()^{{\it\sigma}},G_{0})\rightarrow 1\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow H^{{\it\sigma}}\rightarrow G^{{\it\sigma}}\rightarrow G_{0}^{{\it\sigma}}\rightarrow 1\rightarrow H^{1}(()^{{\it\sigma}},G)\rightarrow H^{1}(()^{{\it\sigma}},G_{0})\rightarrow 1\end{eqnarray}$$and
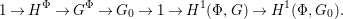 $$\begin{eqnarray}1\rightarrow H^{{\rm\Phi}}\rightarrow G^{{\rm\Phi}}\rightarrow G_{0}\rightarrow 1\rightarrow H^{1}({\rm\Phi},G)\rightarrow H^{1}({\rm\Phi},G_{0}).\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow H^{{\rm\Phi}}\rightarrow G^{{\rm\Phi}}\rightarrow G_{0}\rightarrow 1\rightarrow H^{1}({\rm\Phi},G)\rightarrow H^{1}({\rm\Phi},G_{0}).\end{eqnarray}$$ Since ![]() $H^{{\rm\Phi}}$ is finite, (2) implies that
$H^{{\rm\Phi}}$ is finite, (2) implies that ![]() $G^{{\rm\Phi}}$ is a finite subgroup of
$G^{{\rm\Phi}}$ is a finite subgroup of ![]() $G$ that maps onto
$G$ that maps onto ![]() $G_{0}$. But (1) shows that
$G_{0}$. But (1) shows that 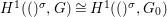 $H^{1}(()^{{\it\sigma}},G)\cong H^{1}(()^{{\it\sigma}},G_{0})$ and thus
$H^{1}(()^{{\it\sigma}},G)\cong H^{1}(()^{{\it\sigma}},G_{0})$ and thus ![]() $G^{{\rm\Phi}}$ also maps onto
$G^{{\rm\Phi}}$ also maps onto 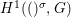 $H^{1}(()^{{\it\sigma}},G)$, which proves the “moreover” clause by 5.4. ◻
$H^{1}(()^{{\it\sigma}},G)$, which proves the “moreover” clause by 5.4. ◻
Definition 5.21. Let 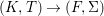 $(K,T)\rightarrow (F,{\rm\Sigma})$ be an extension of difference fields with finite structures
$(K,T)\rightarrow (F,{\rm\Sigma})$ be an extension of difference fields with finite structures ![]() $T$ and
$T$ and ![]() ${\rm\Sigma}$, and let
${\rm\Sigma}$, and let ![]() $(L,{\rm\Sigma})$ be the relative algebraic closure of
$(L,{\rm\Sigma})$ be the relative algebraic closure of ![]() $K$ in
$K$ in ![]() $F$. We say that an extension
$F$. We say that an extension 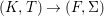 $(K,T)\rightarrow (F,{\rm\Sigma})$ is a weak difference cover if
$(K,T)\rightarrow (F,{\rm\Sigma})$ is a weak difference cover if ![]() $L/K$ is Galois and
$L/K$ is Galois and ![]() ${\rm\Sigma}$ contains a (finite) set of representatives of the isomorphism classes of lifts of all
${\rm\Sigma}$ contains a (finite) set of representatives of the isomorphism classes of lifts of all ![]() ${\it\tau}\in T$ to
${\it\tau}\in T$ to ![]() $L$.
$L$.
Definition 5.22. Let 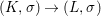 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a separable algebraic
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ be a separable algebraic ![]() ${\it\sigma}$-separable extension of difference fields of finite
${\it\sigma}$-separable extension of difference fields of finite ![]() ${\it\sigma}$-type. Let
${\it\sigma}$-type. Let ![]() $(\tilde{L},{\rm\Sigma})$ be the Galois closure of
$(\tilde{L},{\rm\Sigma})$ be the Galois closure of ![]() $(L,{\it\sigma})$ over
$(L,{\it\sigma})$ over ![]() $(K,{\it\sigma})$ as in 5.16. Note that
$(K,{\it\sigma})$ as in 5.16. Note that ![]() ${\rm\Sigma}$ will often be infinite.
${\rm\Sigma}$ will often be infinite.
We use 5.20 to find ![]() $(\tilde{L},{\rm\Sigma}_{0})$ where the finite
$(\tilde{L},{\rm\Sigma}_{0})$ where the finite ![]() ${\rm\Sigma}_{0}\subseteq {\rm\Sigma}$ represents all lifts of
${\rm\Sigma}_{0}\subseteq {\rm\Sigma}$ represents all lifts of ![]() ${\it\sigma}$ from
${\it\sigma}$ from ![]() $K$ to
$K$ to ![]() $\tilde{L}$, and we let
$\tilde{L}$, and we let 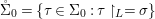 $\mathring{\Sigma}_{0}=\{{\it\tau}\in {\rm\Sigma}_{0}:{\it\tau}\restriction_{L}={\it\sigma}\}$. Then
$\mathring{\Sigma}_{0}=\{{\it\tau}\in {\rm\Sigma}_{0}:{\it\tau}\restriction_{L}={\it\sigma}\}$. Then  $(K,{\it\sigma})\rightarrow (\tilde{L},{\rm\Sigma}_{0})$ and
$(K,{\it\sigma})\rightarrow (\tilde{L},{\rm\Sigma}_{0})$ and  $(L,{\it\sigma})\rightarrow (\tilde{L},\mathring{\Sigma}_{0})$ are weak difference covers and the associated diagram is called the weak Galois closure of
$(L,{\it\sigma})\rightarrow (\tilde{L},\mathring{\Sigma}_{0})$ are weak difference covers and the associated diagram is called the weak Galois closure of ![]() $(L,{\it\sigma})$ over
$(L,{\it\sigma})$ over ![]() $(K,{\it\sigma})$.
$(K,{\it\sigma})$.
Definition 5.23. Let  $(X,{\rm\Sigma})\rightarrow (Y,T)$ be a dominant morphism of transformally integral difference schemes. We shall say that it is a generic weak cover if the corresponding inclusion of function fields
$(X,{\rm\Sigma})\rightarrow (Y,T)$ be a dominant morphism of transformally integral difference schemes. We shall say that it is a generic weak cover if the corresponding inclusion of function fields 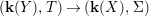 $(\mathbf{k}(Y),T)\rightarrow (\mathbf{k}(X),{\rm\Sigma})$ is a weak difference cover of fields.
$(\mathbf{k}(Y),T)\rightarrow (\mathbf{k}(X),{\rm\Sigma})$ is a weak difference cover of fields.
Definition 5.24. Let 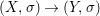 $(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a generically étale
$(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a generically étale ![]() ${\it\sigma}$-separable morphism of transformally integral normal difference schemes, and denote by
${\it\sigma}$-separable morphism of transformally integral normal difference schemes, and denote by 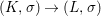 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ the corresponding extension of function fields, let
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ the corresponding extension of function fields, let ![]() $(\tilde{L},{\rm\Sigma}_{0})$ and
$(\tilde{L},{\rm\Sigma}_{0})$ and ![]() $\mathring{\Sigma}_{0}$ be as in 5.22, and write
$\mathring{\Sigma}_{0}$ be as in 5.22, and write  ${\it\iota}:\mathring{\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}_{0}$. Let
${\it\iota}:\mathring{\Sigma}_{0}{\hookrightarrow}{\rm\Sigma}_{0}$. Let ![]() $(\tilde{X},{\rm\Sigma}_{0})$ be the normalization of
$(\tilde{X},{\rm\Sigma}_{0})$ be the normalization of ![]() $Y$ in
$Y$ in ![]() $(\tilde{L},{\rm\Sigma}_{0})$. We obtain a diagram
$(\tilde{L},{\rm\Sigma}_{0})$. We obtain a diagram
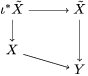
in which the vertical arrows are weak generic covers, called the (generic) weak Galois closure of ![]() $X$ over
$X$ over ![]() $Y$.
$Y$.
Proposition 5.25. Let 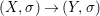 $(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a generically dominant generically smooth morphism of integral normal almost-strict difference schemes. Then it can be subsumed in a generic weak cover in the sense that there exists a diagram
$(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a generically dominant generically smooth morphism of integral normal almost-strict difference schemes. Then it can be subsumed in a generic weak cover in the sense that there exists a diagram
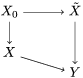
where  $(X_{0},{\rm\Sigma}_{0})\rightarrow (X,{\it\sigma})$ and
$(X_{0},{\rm\Sigma}_{0})\rightarrow (X,{\it\sigma})$ and 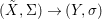 $(\tilde{X},{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ are generic weak covers.
$(\tilde{X},{\rm\Sigma})\rightarrow (Y,{\it\sigma})$ are generic weak covers.
Proof. Let ![]() $(L,{\it\sigma})$ be the relative algebraic closure of
$(L,{\it\sigma})$ be the relative algebraic closure of ![]() $\mathbf{k}(Y)$ inside
$\mathbf{k}(Y)$ inside ![]() $\mathbf{k}(X)$, and let
$\mathbf{k}(X)$, and let ![]() $\bar{Y}$ be the normalization of
$\bar{Y}$ be the normalization of ![]() $Y$ in
$Y$ in ![]() $L$. As in 5.24, let
$L$. As in 5.24, let ![]() $({\tilde{Y}},{\rm\Sigma})$,
$({\tilde{Y}},{\rm\Sigma})$, 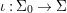 ${\it\iota}:{\rm\Sigma}_{0}\rightarrow {\rm\Sigma}$ be the data associated with the quasi-Galois closure
${\it\iota}:{\rm\Sigma}_{0}\rightarrow {\rm\Sigma}$ be the data associated with the quasi-Galois closure ![]() ${\it\iota}^{\ast }{\tilde{Y}}$ of
${\it\iota}^{\ast }{\tilde{Y}}$ of ![]() $\bar{Y}$ over
$\bar{Y}$ over ![]() $Y$, and let
$Y$, and let 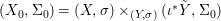 $(X_{0},{\rm\Sigma}_{0})=(X,{\it\sigma})\times _{(Y,{\it\sigma})}({\it\iota}^{\ast }{\tilde{Y}},{\rm\Sigma}_{0})$. The diagram obtained using 4.8
$(X_{0},{\rm\Sigma}_{0})=(X,{\it\sigma})\times _{(Y,{\it\sigma})}({\it\iota}^{\ast }{\tilde{Y}},{\rm\Sigma}_{0})$. The diagram obtained using 4.8
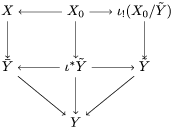
shows the required statement with 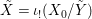 $\tilde{X}={\it\iota}_{!}(X_{0}/{\tilde{Y}})$ in a very explicit way.◻
$\tilde{X}={\it\iota}_{!}(X_{0}/{\tilde{Y}})$ in a very explicit way.◻
6 Effective difference algebraic geometry
As mentioned in the Introduction, one of the main benefits of our Galois stratification procedure is that it makes the quantifier elimination and decision procedures for fields with Frobenii effective in an adequate sense of the word to be expounded in this section.
Ideally, we would like to prove that it makes those procedures primitive recursive, which would represent a significant improvement on the known results [Reference Macintyre21], [Reference Chatzidakis and Hrushovski6], [Reference Hrushovski18], where it was shown that the decision procedure is recursive.
Unfortunately, due to the underdeveloped state of constructive difference algebra, and the lack of algorithms for relevant operations with difference-polynomial ideals, all we can do at the moment is to show that our Galois stratification procedure is primitive recursive reducible to a number of oracles for basic operations in difference algebra, which we hope will be shown to be primitive recursive themselves.
For a reader critical of this hybrid notion of effectiveness, let us mention that we have developed the theory of Galois stratification in the context of directly presented difference schemes, and the resulting quantifier elimination, equivalent in power to the logic quantifier elimination but coarser than the one in the present paper, is shown to be unconditionally primitive recursive in [Reference Tomašić23]. As is often the case in difference and differential algebra, a coarser result turns out to be more effective.
Definition 6.1. A ring ![]() $(R,{\it\sigma})$ is said to be effectively presented, if it has a finite
$(R,{\it\sigma})$ is said to be effectively presented, if it has a finite ![]() ${\it\sigma}$-presentation over
${\it\sigma}$-presentation over ![]() $\mathbb{Z}$, with its generators and relations explicitly given.
$\mathbb{Z}$, with its generators and relations explicitly given.
The following is a list of elementary operations on effectively presented rings that we shall have recourse to in the sequel.
(†1) Given a difference ideal
 $I$ in a difference-polynomial ring over an effectively presented difference field, find its minimal associated
$I$ in a difference-polynomial ring over an effectively presented difference field, find its minimal associated  ${\it\sigma}$-primes, that is, find an irredundant decomposition
${\it\sigma}$-primes, that is, find an irredundant decomposition  $\{I\}_{{\it\sigma}}=\mathfrak{p}_{1}\cap \cdots \cap \mathfrak{p}_{n}$ (as in [Reference Tomašić24, 2.45]).
$\{I\}_{{\it\sigma}}=\mathfrak{p}_{1}\cap \cdots \cap \mathfrak{p}_{n}$ (as in [Reference Tomašić24, 2.45]).(†2) Given an extension
 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of effectively presented difference fields of finite
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of effectively presented difference fields of finite  ${\it\sigma}$-type, compute the relative algebraic closure of
${\it\sigma}$-type, compute the relative algebraic closure of  $K$ in
$K$ in  $L$.
$L$.(†3) In the situation of (†2), compute a decomposition into a
 ${\it\sigma}$-separable and
${\it\sigma}$-separable and  ${\it\sigma}$-radicial part as in 3.47.
${\it\sigma}$-radicial part as in 3.47.(†4) Given an
 ${\it\sigma}$-separable Galois extension
${\it\sigma}$-separable Galois extension  $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of effectively presented difference fields of finite
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of effectively presented difference fields of finite  ${\it\sigma}$-type, compute its Babbitt’s decomposition (as in 5.11).
${\it\sigma}$-type, compute its Babbitt’s decomposition (as in 5.11).(†5) For an effectively presented integrally closed domain
 $(R,{\it\sigma})$ with fraction field
$(R,{\it\sigma})$ with fraction field  $(K,{\it\sigma})$, and an extension
$(K,{\it\sigma})$, and an extension  $(L,{\it\sigma})$ of
$(L,{\it\sigma})$ of  $(K,{\it\sigma})$ of finite
$(K,{\it\sigma})$ of finite  ${\it\sigma}$-type, find the integral closure
${\it\sigma}$-type, find the integral closure  $(S,{\it\sigma})$ of
$(S,{\it\sigma})$ of  $R$ in
$R$ in  $L$, and compute the
$L$, and compute the  ${\it\sigma}$-localization
${\it\sigma}$-localization  $(R^{\prime },{\it\sigma})$ of
$(R^{\prime },{\it\sigma})$ of  $R$ so that the corresponding
$R$ so that the corresponding  $S^{\prime }$ is of finite
$S^{\prime }$ is of finite  ${\it\sigma}$-type over
${\it\sigma}$-type over  $R^{\prime }$ [Reference Tomašić24, 2.56].
$R^{\prime }$ [Reference Tomašić24, 2.56].(†6) Given an effectively presented morphism
 $f:(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ of effectively presented difference rings and a suitable property
$f:(R,{\it\sigma})\rightarrow (S,{\it\sigma})$ of effectively presented difference rings and a suitable property  $P$ of scheme morphisms, if
$P$ of scheme morphisms, if  $f$ is generically
$f$ is generically  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$, compute the
$P$, compute the  ${\it\sigma}$-localizations
${\it\sigma}$-localizations  $R^{\prime }$ of
$R^{\prime }$ of  $R$ and
$R$ and  $S^{\prime }$ of
$S^{\prime }$ of  $S$ such that
$S$ such that  $(R^{\prime },{\it\sigma})\rightarrow (S^{\prime },{\it\sigma})$ is
$(R^{\prime },{\it\sigma})\rightarrow (S^{\prime },{\it\sigma})$ is  ${\it\sigma}$-pro-
${\it\sigma}$-pro- $P$ (in particular, we need effective versions of 3.8, 3.14 and 3.9).
$P$ (in particular, we need effective versions of 3.8, 3.14 and 3.9).(†7) Given an algebraic extension
 $(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of effectively presented difference fields of finite
$(K,{\it\sigma})\rightarrow (L,{\it\sigma})$ of effectively presented difference fields of finite  ${\it\sigma}$-type, compute the quasi-Galois closure of
${\it\sigma}$-type, compute the quasi-Galois closure of  $L$ over
$L$ over  $K$.
$K$.(†8) For a finite Galois extension
 $(K,{\it\sigma})\rightarrow (L,{\rm\Sigma})$ of effectively presented difference fields, establish an effective correspondence between the intermediate field extensions and subgroups of the Galois group.
$(K,{\it\sigma})\rightarrow (L,{\rm\Sigma})$ of effectively presented difference fields, establish an effective correspondence between the intermediate field extensions and subgroups of the Galois group.(†9) Effective Twisted Lang–Weil estimate. In the situation of [Reference Tomašić24, 4.2], compute explicitly the constant
 $C$ and the localization
$C$ and the localization  $S^{\prime }$ of
$S^{\prime }$ of  $S$.
$S$.
Definition 6.2. We define ![]() $\dagger$-primitive recursive functions as functions primitive recursive reducible to basic operations in Difference Algebraic Geometry as detailed by the following axioms.
$\dagger$-primitive recursive functions as functions primitive recursive reducible to basic operations in Difference Algebraic Geometry as detailed by the following axioms.
Basic ![]() $\dagger$-primitive recursive functions are:
$\dagger$-primitive recursive functions are:
(1) Constant functions, Successor function
 $S$, coordinate Projections;
$S$, coordinate Projections;(2) Elementary operations in difference algebraic geometry (†1)–(†9).
More complex ![]() $\dagger$-primitive recursive functions are built using:
$\dagger$-primitive recursive functions are built using:
(3) Composition. If
 $f$ is an
$f$ is an  $n$-ary
$n$-ary  $\dagger$-primitive recursive function, and
$\dagger$-primitive recursive function, and  $g_{1},\ldots ,g_{n}$ are
$g_{1},\ldots ,g_{n}$ are  $m$-ary
$m$-ary  $\dagger$-primitive recursive function, then is
$\dagger$-primitive recursive function, then is $$\begin{eqnarray}h(x_{1},\ldots ,x_{m})=f(g_{1}(x_{1},\ldots ,x_{m}),\ldots ,g_{n}(x_{1},\ldots ,x_{m}))\end{eqnarray}$$
$$\begin{eqnarray}h(x_{1},\ldots ,x_{m})=f(g_{1}(x_{1},\ldots ,x_{m}),\ldots ,g_{n}(x_{1},\ldots ,x_{m}))\end{eqnarray}$$ $\dagger$-primitive recursive.
$\dagger$-primitive recursive.(3) Primitive recursion. Suppose
 $f$ is an
$f$ is an  $n$-ary and
$n$-ary and  $g$ is an
$g$ is an  $(n+2)$-ary
$(n+2)$-ary  $\dagger$-primitive recursive function. The function
$\dagger$-primitive recursive function. The function  $h$, defined by is
$h$, defined by is $$\begin{eqnarray}\displaystyle h(0,x_{1},\ldots ,x_{n}) & = & \displaystyle f(x_{1},\ldots ,x_{n})\nonumber\\ \displaystyle h(S(y),x_{1},\ldots ,x_{n}) & = & \displaystyle g(y,h(y,x_{1},\ldots ,x_{n}),x_{1},\ldots ,x_{n})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(0,x_{1},\ldots ,x_{n}) & = & \displaystyle f(x_{1},\ldots ,x_{n})\nonumber\\ \displaystyle h(S(y),x_{1},\ldots ,x_{n}) & = & \displaystyle g(y,h(y,x_{1},\ldots ,x_{n}),x_{1},\ldots ,x_{n})\nonumber\end{eqnarray}$$ $\dagger$-primitive recursive.
$\dagger$-primitive recursive.
Proof. In view of the constructive nature of proofs of 3.3, 3.7, 3.8, 3.14, 3.9, the fact that the operation (†6) is primitive recursive will follow from the existence of the classical primitive recursive procedure for finding a localization satisfying the property ![]() $P$ at the start of the prolongation sequence.
$P$ at the start of the prolongation sequence.
The operation (†7) is primitive recursive because the construction of quasi-Galois closure is primitive recursive in the algebraic case. Indeed, if 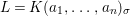 $L=K(a_{1},\ldots ,a_{n})_{{\it\sigma}}$, and
$L=K(a_{1},\ldots ,a_{n})_{{\it\sigma}}$, and  $K(b_{1},\ldots ,b_{m})$ is the quasi-Galois closure of
$K(b_{1},\ldots ,b_{m})$ is the quasi-Galois closure of  $K(a_{1},\ldots ,a_{n})$, then
$K(a_{1},\ldots ,a_{n})$, then 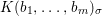 $K(b_{1},\ldots ,b_{m})_{{\it\sigma}}$ is the quasi-Galois closure of
$K(b_{1},\ldots ,b_{m})_{{\it\sigma}}$ is the quasi-Galois closure of ![]() $L$.
$L$.
Since the operation (†8) only deals with finite Galois extensions, it follows that it is primitive recursive by the discussion in [Reference Fried and Sacerdote14].
Regarding (†9), Hrushovski indicates in the “Decidability” subsection following [Reference Hrushovski18, 13.2] that it is effective, showing how to explicitly compute the constants for the error term. ◻
7 Galois stratification
7.1 Galois stratifications and Galois formulas
Definition 7.1. Let ![]() $(X,{\it\sigma})$ be an
$(X,{\it\sigma})$ be an ![]() $(S,{\it\sigma})$-difference scheme. It is often useful to consider its realization functor
$(S,{\it\sigma})$-difference scheme. It is often useful to consider its realization functor ![]() $\tilde{X}$. For each
$\tilde{X}$. For each ![]() $s\in S$ and each algebraically closed difference field
$s\in S$ and each algebraically closed difference field ![]() $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending 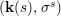 $(\mathbf{k}(s),{\it\sigma}^{s})$,
$(\mathbf{k}(s),{\it\sigma}^{s})$,
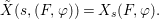 $$\begin{eqnarray}\tilde{X}(s,(F,{\it\varphi}))=X_{s}(F,{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{X}(s,(F,{\it\varphi}))=X_{s}(F,{\it\varphi}).\end{eqnarray}$$ An ![]() $(S,{\it\sigma})$-subassignment of
$(S,{\it\sigma})$-subassignment of ![]() $X$ is any subfunctor
$X$ is any subfunctor ![]() ${\mathcal{F}}$ of
${\mathcal{F}}$ of ![]() $\tilde{X}$. Namely, for any
$\tilde{X}$. Namely, for any 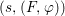 $(s,(F,{\it\varphi}))$ as above,
$(s,(F,{\it\varphi}))$ as above,
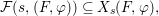 $$\begin{eqnarray}{\mathcal{F}}(s,(F,{\it\varphi}))\subseteq X_{s}(F,{\it\varphi}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}(s,(F,{\it\varphi}))\subseteq X_{s}(F,{\it\varphi}),\end{eqnarray}$$ and for any 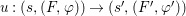 $u:(s,(F,{\it\varphi}))\rightarrow (s^{\prime },(F^{\prime },{\it\varphi}^{\prime }))$,
$u:(s,(F,{\it\varphi}))\rightarrow (s^{\prime },(F^{\prime },{\it\varphi}^{\prime }))$, ![]() ${\mathcal{F}}(u)$ is the restriction of
${\mathcal{F}}(u)$ is the restriction of ![]() $\tilde{X}(u)$ to
$\tilde{X}(u)$ to 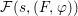 ${\mathcal{F}}(s,(F,{\it\varphi}))$.
${\mathcal{F}}(s,(F,{\it\varphi}))$.
Definition 7.2. Let ![]() $(S,{\it\sigma})$ be a difference scheme and let
$(S,{\it\sigma})$ be a difference scheme and let ![]() $(X,{\it\sigma})$ be a difference scheme over
$(X,{\it\sigma})$ be a difference scheme over ![]() $(S,{\it\sigma})$. A normal (twisted) Galois stratification
$(S,{\it\sigma})$. A normal (twisted) Galois stratification
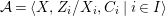 $$\begin{eqnarray}{\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\mid i\in I\rangle\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\mid i\in I\rangle\end{eqnarray}$$ of ![]() $(X,{\it\sigma})$ over
$(X,{\it\sigma})$ over ![]() $(S,{\it\sigma})$ is a partition of
$(S,{\it\sigma})$ is a partition of ![]() $(X,{\it\sigma})$ into a finite set of transformally integral normal
$(X,{\it\sigma})$ into a finite set of transformally integral normal ![]() ${\it\sigma}$-locally closed difference
${\it\sigma}$-locally closed difference ![]() $(S,{\it\sigma})$-subvarieties
$(S,{\it\sigma})$-subvarieties ![]() $(X_{i},{\it\sigma})$ of
$(X_{i},{\it\sigma})$ of ![]() $(X,{\it\sigma})$, each equipped with a transformally integral étale Galois cover
$(X,{\it\sigma})$, each equipped with a transformally integral étale Galois cover 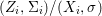 $(Z_{i},{\rm\Sigma}_{i})/(X_{i},{\it\sigma})$ with group
$(Z_{i},{\rm\Sigma}_{i})/(X_{i},{\it\sigma})$ with group 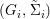 $(G_{i},\tilde{{\rm\Sigma}}_{i})$, and
$(G_{i},\tilde{{\rm\Sigma}}_{i})$, and ![]() $C_{i}$ is a “conjugacy domain” in
$C_{i}$ is a “conjugacy domain” in ![]() ${\rm\Sigma}_{i}$.
${\rm\Sigma}_{i}$.
A normal Galois stratification is effectively given, if the base ![]() $(S,{\it\sigma})$ and all the pieces
$(S,{\it\sigma})$ and all the pieces ![]() $Z_{i}$,
$Z_{i}$, ![]() $X_{i}$ are affine with effectively presented coordinate rings (i.e., of finite
$X_{i}$ are affine with effectively presented coordinate rings (i.e., of finite ![]() ${\it\sigma}$-presentation over
${\it\sigma}$-presentation over ![]() $\mathbb{Z}$).
$\mathbb{Z}$).
Definition 7.3. We define the (twisted) Galois formula over ![]() $(S,{\it\sigma})$ associated with the above stratification
$(S,{\it\sigma})$ associated with the above stratification ![]() ${\mathcal{A}}$ to be its realization subassignment
${\mathcal{A}}$ to be its realization subassignment ![]() $\tilde{{\mathcal{A}}}$ of
$\tilde{{\mathcal{A}}}$ of ![]() $X$. Given a point
$X$. Given a point ![]() $s\in S$ and an algebraically closed difference field
$s\in S$ and an algebraically closed difference field ![]() $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending 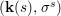 $(\mathbf{k}(s),{\it\sigma}^{s})$,
$(\mathbf{k}(s),{\it\sigma}^{s})$,
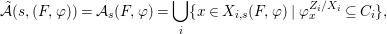 $$\begin{eqnarray}\tilde{{\mathcal{A}}}(s,(F,{\it\varphi}))={\mathcal{A}}_{s}(F,{\it\varphi})=\mathop{\bigcup }_{i}\{x\in X_{i,s}(F,{\it\varphi})\mid {\it\varphi}_{x}^{Z_{i}/X_{i}}\subseteq C_{i}\},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{A}}}(s,(F,{\it\varphi}))={\mathcal{A}}_{s}(F,{\it\varphi})=\mathop{\bigcup }_{i}\{x\in X_{i,s}(F,{\it\varphi})\mid {\it\varphi}_{x}^{Z_{i}/X_{i}}\subseteq C_{i}\},\end{eqnarray}$$ where ![]() ${\it\varphi}_{x}^{Z_{i}/X_{i}}$ denotes the local
${\it\varphi}_{x}^{Z_{i}/X_{i}}$ denotes the local ![]() ${\it\varphi}$-substitution at
${\it\varphi}$-substitution at ![]() $x$ (see 3.44).
$x$ (see 3.44).
It can be beneficial to think of the Galois formula associated with ![]() ${\mathcal{A}}$ and a given parameter
${\mathcal{A}}$ and a given parameter ![]() $s\in S$ as of the formal expression
$s\in S$ as of the formal expression
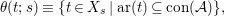 $$\begin{eqnarray}{\it\theta}(t;s)\equiv \{t\in X_{s}\mid \text{ar}(t)\subseteq \text{con}({\mathcal{A}})\},\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}(t;s)\equiv \{t\in X_{s}\mid \text{ar}(t)\subseteq \text{con}({\mathcal{A}})\},\end{eqnarray}$$ whose interpretation in any given ![]() $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending 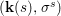 $(\mathbf{k}(s),{\it\sigma}^{s})$ is given above. Namely, the “Artin symbol”
$(\mathbf{k}(s),{\it\sigma}^{s})$ is given above. Namely, the “Artin symbol” ![]() $\text{ar}(t)$ of a point
$\text{ar}(t)$ of a point 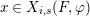 $x\in X_{i,s}(F,{\it\varphi})$ is interpreted as
$x\in X_{i,s}(F,{\it\varphi})$ is interpreted as 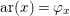 $\text{ar}(x)={\it\varphi}_{x}$, the local
$\text{ar}(x)={\it\varphi}_{x}$, the local ![]() ${\it\varphi}$-substitution at
${\it\varphi}$-substitution at ![]() $x$ with respect to the cover
$x$ with respect to the cover ![]() $Z_{i}/X_{i}$, and
$Z_{i}/X_{i}$, and ![]() $\text{con}({\mathcal{A}})$ at
$\text{con}({\mathcal{A}})$ at ![]() $x$ becomes the appropriate
$x$ becomes the appropriate ![]() $C_{i}$.
$C_{i}$.
Remark 7.4. If we fix a lift ![]() ${\it\sigma}_{i}\in {\rm\Sigma}_{i}$ of
${\it\sigma}_{i}\in {\rm\Sigma}_{i}$ of ![]() ${\it\sigma}$ for each
${\it\sigma}$ for each ![]() $i$ as in 3.45, the above data is equivalent to fixing for each
$i$ as in 3.45, the above data is equivalent to fixing for each ![]() $i$ a
$i$ a ![]() $\text{}^{{\it\sigma}_{i}}()$-conjugacy domain
$\text{}^{{\it\sigma}_{i}}()$-conjugacy domain ![]() ${\dot{C}}_{i}$ in
${\dot{C}}_{i}$ in ![]() $G_{i}$, that is, a union of
$G_{i}$, that is, a union of ![]() $\text{}^{{\it\sigma}_{i}}()$-conjugacy classes in
$\text{}^{{\it\sigma}_{i}}()$-conjugacy classes in ![]() $G_{i}$. This justifies the adjective “twisted” used alongside “stratification”. Clearly,
$G_{i}$. This justifies the adjective “twisted” used alongside “stratification”. Clearly,
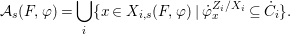 $$\begin{eqnarray}{\mathcal{A}}_{s}(F,{\it\varphi})=\mathop{\bigcup }_{i}\{x\in X_{i,s}(F,{\it\varphi})\mid \dot{{\it\varphi}}_{x}^{Z_{i}/X_{i}}\subseteq {\dot{C}}_{i}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{s}(F,{\it\varphi})=\mathop{\bigcup }_{i}\{x\in X_{i,s}(F,{\it\varphi})\mid \dot{{\it\varphi}}_{x}^{Z_{i}/X_{i}}\subseteq {\dot{C}}_{i}\}.\end{eqnarray}$$Definition 7.5. Let 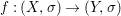 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be an
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be an ![]() $(S,{\it\varphi})$-morphism, let
$(S,{\it\varphi})$-morphism, let 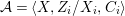 ${\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\rangle$ be an
${\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\rangle$ be an ![]() $(S,{\it\sigma})$-Galois stratification on
$(S,{\it\sigma})$-Galois stratification on ![]() $X$ and let
$X$ and let  ${\mathcal{B}}=\langle Y,W_{j}/Y_{j},D_{j}\rangle$ be an
${\mathcal{B}}=\langle Y,W_{j}/Y_{j},D_{j}\rangle$ be an ![]() $(S,{\it\sigma})$-Galois stratification on
$(S,{\it\sigma})$-Galois stratification on ![]() $Y$.
$Y$.
(1) Given étale Galois
 $(S,{\it\varphi})$-covers
$(S,{\it\varphi})$-covers  $(Z_{i}^{\prime },{\rm\Sigma}_{i}^{\prime })\rightarrow (X_{i},{\it\sigma})$ that dominate
$(Z_{i}^{\prime },{\rm\Sigma}_{i}^{\prime })\rightarrow (X_{i},{\it\sigma})$ that dominate  $Z_{i}/X_{i}$, and writing
$Z_{i}/X_{i}$, and writing  ${\it\pi}_{i}:{\rm\Sigma}_{i}^{\prime }\rightarrow {\rm\Sigma}_{i}$ for the relevant
${\it\pi}_{i}:{\rm\Sigma}_{i}^{\prime }\rightarrow {\rm\Sigma}_{i}$ for the relevant  $\mathit{Diff}$-morphisms, the inflation of
$\mathit{Diff}$-morphisms, the inflation of  ${\mathcal{A}}$with respect to covers
${\mathcal{A}}$with respect to covers  $Z_{i}^{\prime }/X_{i}$ is defined asIt has the property that for every
$Z_{i}^{\prime }/X_{i}$ is defined asIt has the property that for every $$\begin{eqnarray}{\mathcal{A}}^{\prime }=\langle X,Z_{i}^{\prime }/X_{i},{\it\pi}_{i}^{-1}(C_{i})\rangle .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}^{\prime }=\langle X,Z_{i}^{\prime }/X_{i},{\it\pi}_{i}^{-1}(C_{i})\rangle .\end{eqnarray}$$ $s\in S$, and every algebraically closed
$s\in S$, and every algebraically closed  $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending  $(\mathbf{k}(s),{\it\sigma}^{s})$,
$(\mathbf{k}(s),{\it\sigma}^{s})$,  $$\begin{eqnarray}{\mathcal{A}}_{s}^{\prime }(F,{\it\varphi})={\mathcal{A}}_{s}(F,{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{s}^{\prime }(F,{\it\varphi})={\mathcal{A}}_{s}(F,{\it\varphi}).\end{eqnarray}$$(2) Suppose we are given a further stratification of each
 $X_{i}$ into finitely many integral, normal, locally closed
$X_{i}$ into finitely many integral, normal, locally closed  $(S,{\it\sigma})$-subschemes
$(S,{\it\sigma})$-subschemes  $X_{ij}$. For each
$X_{ij}$. For each  $i,j$, let
$i,j$, let  $Z_{ij}$ be a connected component of
$Z_{ij}$ be a connected component of  $(Z_{i},{\rm\Sigma}_{i})\times _{(X_{i},{\it\sigma})}(X_{ij},{\it\sigma})$, and let
$(Z_{i},{\rm\Sigma}_{i})\times _{(X_{i},{\it\sigma})}(X_{ij},{\it\sigma})$, and let  $D_{ij}$ be its decomposition subgroup in
$D_{ij}$ be its decomposition subgroup in  $Z_{i}/X_{i}$. Moreover, let
$Z_{i}/X_{i}$. Moreover, let  ${\rm\Sigma}_{ij}=\{{\it\sigma}\in {\rm\Sigma}_{i}:{\it\sigma}Z_{ij}=Z_{ij}\}$ and write
${\rm\Sigma}_{ij}=\{{\it\sigma}\in {\rm\Sigma}_{i}:{\it\sigma}Z_{ij}=Z_{ij}\}$ and write  ${\it\iota}_{ij}:{\rm\Sigma}_{ij}{\hookrightarrow}{\rm\Sigma}_{i}$. Then
${\it\iota}_{ij}:{\rm\Sigma}_{ij}{\hookrightarrow}{\rm\Sigma}_{i}$. Then  $(Z_{ij},T_{ij})\rightarrow (X_{ij},{\it\sigma})$ is a Galois cover over
$(Z_{ij},T_{ij})\rightarrow (X_{ij},{\it\sigma})$ is a Galois cover over  $(S,{\it\sigma})$ with group
$(S,{\it\sigma})$ with group  $(D_{ij},\tilde{{\rm\Sigma}}_{ij})$.
$(D_{ij},\tilde{{\rm\Sigma}}_{ij})$.The refinement of
 ${\mathcal{A}}$to the stratification
${\mathcal{A}}$to the stratification  $\{X_{ij}\}$of
$\{X_{ij}\}$of  $X$ is defined as It has the property that for every
$X$ is defined as It has the property that for every $$\begin{eqnarray}{\mathcal{A}}^{\prime }=\langle X,Z_{ij}/X_{ij},{\it\iota}_{ij}^{-1}(C_{i})\rangle .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}^{\prime }=\langle X,Z_{ij}/X_{ij},{\it\iota}_{ij}^{-1}(C_{i})\rangle .\end{eqnarray}$$ $s\in S$, and every algebraically closed
$s\in S$, and every algebraically closed  $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending  $(\mathbf{k}(s),{\it\sigma}^{s})$,
$(\mathbf{k}(s),{\it\sigma}^{s})$,  $$\begin{eqnarray}{\mathcal{A}}_{s}^{\prime }(F,{\it\varphi})={\mathcal{A}}_{s}(F,{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{s}^{\prime }(F,{\it\varphi})={\mathcal{A}}_{s}(F,{\it\varphi}).\end{eqnarray}$$(3) Let
 $Z_{j}$ be a component of
$Z_{j}$ be a component of  $(X,{\it\sigma})\times _{(Y,{\it\sigma})}(W_{j},T)$, and let
$(X,{\it\sigma})\times _{(Y,{\it\sigma})}(W_{j},T)$, and let  $D_{Z_{j}}$ be its decomposition subgroup in
$D_{Z_{j}}$ be its decomposition subgroup in  $W_{j}/Y_{j}$. Moreover, let
$W_{j}/Y_{j}$. Moreover, let  $T_{Z_{j}}=\{{\it\tau}\in T_{j}:{\it\tau}Z_{j}=Z_{j}\}$ and write
$T_{Z_{j}}=\{{\it\tau}\in T_{j}:{\it\tau}Z_{j}=Z_{j}\}$ and write  ${\it\iota}_{j}:T_{Z_{j}}{\hookrightarrow}T_{j}$. Then
${\it\iota}_{j}:T_{Z_{j}}{\hookrightarrow}T_{j}$. Then  $(Z_{j},T_{Z_{j}})\rightarrow (X_{j},{\it\sigma})=f^{-1}(Y_{j})$ is a Galois cover with group
$(Z_{j},T_{Z_{j}})\rightarrow (X_{j},{\it\sigma})=f^{-1}(Y_{j})$ is a Galois cover with group  $(D_{Z_{j}},\tilde{T}_{Z_{j}})$.
$(D_{Z_{j}},\tilde{T}_{Z_{j}})$.The pullback
 $f^{\ast }{\mathcal{B}}$ of
$f^{\ast }{\mathcal{B}}$ of  ${\mathcal{B}}$ with respect to
${\mathcal{B}}$ with respect to  $f$ is defined as a refinement of to a normal refinement (noncanonical, found by 3.9) of the stratification
$f$ is defined as a refinement of to a normal refinement (noncanonical, found by 3.9) of the stratification $$\begin{eqnarray}\langle X,Z_{j}/X_{j},{\it\iota}_{j}^{-1}(D_{j})\rangle\end{eqnarray}$$
$$\begin{eqnarray}\langle X,Z_{j}/X_{j},{\it\iota}_{j}^{-1}(D_{j})\rangle\end{eqnarray}$$ $X_{j}$ of
$X_{j}$ of  $X$. It has the property that for every
$X$. It has the property that for every  $s\in S$, and every algebraically closed
$s\in S$, and every algebraically closed  $(F,{\it\varphi})$ extending
$(F,{\it\varphi})$ extending  $(\mathbf{k}(s),{\it\sigma}^{s})$,
$(\mathbf{k}(s),{\it\sigma}^{s})$,  $$\begin{eqnarray}f^{\ast }{\mathcal{B}}_{s}(F,{\it\varphi})=f_{s}^{-1}({\mathcal{B}}_{s}(F,{\it\varphi})).\end{eqnarray}$$
$$\begin{eqnarray}f^{\ast }{\mathcal{B}}_{s}(F,{\it\varphi})=f_{s}^{-1}({\mathcal{B}}_{s}(F,{\it\varphi})).\end{eqnarray}$$
Definition 7.6. Let ![]() $(X,{\it\sigma})$ be an
$(X,{\it\sigma})$ be an ![]() $(S,{\it\sigma})$-difference scheme. The class of
$(S,{\it\sigma})$-difference scheme. The class of ![]() $(S,{\it\sigma})$-Galois formulas on
$(S,{\it\sigma})$-Galois formulas on ![]() $X$ has a Boolean algebra structure as follows.
$X$ has a Boolean algebra structure as follows.
(1)
 $\bot _{X}=\langle X,X/X,\emptyset \rangle$,
$\bot _{X}=\langle X,X/X,\emptyset \rangle$,  $\top _{X}=\langle X,X/X,\{{\it\sigma}\}\rangle$.
$\top _{X}=\langle X,X/X,\{{\it\sigma}\}\rangle$.
For Galois formulas on ![]() $X$ given by
$X$ given by ![]() ${\mathcal{A}}$ and
${\mathcal{A}}$ and ![]() ${\mathcal{B}}$, upon a refinement and an inflation we may assume that
${\mathcal{B}}$, upon a refinement and an inflation we may assume that 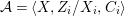 ${\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\rangle$ and
${\mathcal{A}}=\langle X,Z_{i}/X_{i},C_{i}\rangle$ and 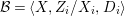 ${\mathcal{B}}=\langle X,Z_{i}/X_{i},D_{i}\rangle$, with
${\mathcal{B}}=\langle X,Z_{i}/X_{i},D_{i}\rangle$, with 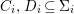 $C_{i},D_{i}\subseteq {\rm\Sigma}_{i}$.
$C_{i},D_{i}\subseteq {\rm\Sigma}_{i}$.
(2)
 ${\mathcal{A}}\wedge {\mathcal{B}}=\langle X,Z_{i}/X_{i},C_{i}\cap D_{i}\rangle$.
${\mathcal{A}}\wedge {\mathcal{B}}=\langle X,Z_{i}/X_{i},C_{i}\cap D_{i}\rangle$.
(3)
 ${\mathcal{A}}\vee {\mathcal{B}}=\langle X,Z_{i}/X_{i},C_{i}\cup D_{i}\rangle$.
${\mathcal{A}}\vee {\mathcal{B}}=\langle X,Z_{i}/X_{i},C_{i}\cup D_{i}\rangle$.
(4)
 $\neg {\mathcal{A}}=\langle X,Z_{i}/X_{i},{\rm\Sigma}_{i}\setminus C_{i}\rangle$.
$\neg {\mathcal{A}}=\langle X,Z_{i}/X_{i},{\rm\Sigma}_{i}\setminus C_{i}\rangle$.
7.2 Direct image theorems
The following result can be considered as a difference version of Chevalley’s theorem stating that a direct image of a constructible set by a scheme morphism of finite presentation is again constructible.
Proposition 7.7. Let 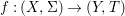 $f:(X,{\rm\Sigma})\rightarrow (Y,T)$ be a generic weak cover of finite transformal type. Then
$f:(X,{\rm\Sigma})\rightarrow (Y,T)$ be a generic weak cover of finite transformal type. Then ![]() $f(X)$ contains a dense open subset of
$f(X)$ contains a dense open subset of ![]() $Y$. If
$Y$. If ![]() $f$ is effectively presented, we can compute it in a
$f$ is effectively presented, we can compute it in a ![]() $\dagger$-primitive recursive way.
$\dagger$-primitive recursive way.
Proof. It is enough to consider the case when 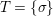 $T=\{{\it\sigma}\}$.
$T=\{{\it\sigma}\}$.
Using 3.47, we can factorize ![]() $f$ as a composite of a radicial (purely inseparable),
$f$ as a composite of a radicial (purely inseparable), ![]() ${\it\sigma}$-radicial and a separable
${\it\sigma}$-radicial and a separable ![]() ${\it\sigma}$-separable morphism. The cases of radicial or
${\it\sigma}$-separable morphism. The cases of radicial or ![]() ${\it\sigma}$-radicial
${\it\sigma}$-radicial ![]() $f$ are dealt with using 3.48, so we reduce to the case of separable
$f$ are dealt with using 3.48, so we reduce to the case of separable ![]() ${\it\sigma}$-separable
${\it\sigma}$-separable ![]() $f$. In the effective situation, this requires (†3).
$f$. In the effective situation, this requires (†3).
By ![]() ${\it\sigma}$-localizing (3.8), we may assume that
${\it\sigma}$-localizing (3.8), we may assume that ![]() $f$ is a
$f$ is a ![]() ${\it\sigma}$-pro-smooth morphism between normal difference schemes. This is
${\it\sigma}$-pro-smooth morphism between normal difference schemes. This is ![]() $\dagger$-primitive recursive by (†9). By considering the normalization
$\dagger$-primitive recursive by (†9). By considering the normalization ![]() ${\tilde{Y}}$ in the relative algebraic closure of
${\tilde{Y}}$ in the relative algebraic closure of ![]() $\mathbf{k}(Y)$ inside
$\mathbf{k}(Y)$ inside ![]() $\mathbf{k}(X)$, we obtain a baby Stein factorization
$\mathbf{k}(X)$, we obtain a baby Stein factorization 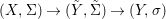 $(X,{\rm\Sigma})\rightarrow ({\tilde{Y}},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$, where the first map has geometrically transformally integral generic fiber (by 3.50), and the second is generically
$(X,{\rm\Sigma})\rightarrow ({\tilde{Y}},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$, where the first map has geometrically transformally integral generic fiber (by 3.50), and the second is generically ![]() ${\it\sigma}$-pro-étale
${\it\sigma}$-pro-étale ![]() ${\it\sigma}$-separable, with
${\it\sigma}$-separable, with 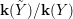 $\mathbf{k}({\tilde{Y}})/\mathbf{k}(Y)$ Galois by definition of weak covers.
$\mathbf{k}({\tilde{Y}})/\mathbf{k}(Y)$ Galois by definition of weak covers.
By localizing further using 3.14, we may assume that all the fibers of the first morphism are directly transformally integral and consequently nonempty, so the first morphism is surjective, and we can restrict our attention to the second morphism. These steps are ![]() $\dagger$-primitive recursive by (†2), (†5), (†6).
$\dagger$-primitive recursive by (†2), (†5), (†6).
Using 3.8, by another localization we restrict to the case where 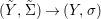 $({\tilde{Y}},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$ is
$({\tilde{Y}},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$ is ![]() ${\it\sigma}$-pro-étale
${\it\sigma}$-pro-étale ![]() ${\it\sigma}$-separable. Applying Babbitt’s decomposition 5.12 to
${\it\sigma}$-separable. Applying Babbitt’s decomposition 5.12 to 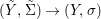 $({\tilde{Y}},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$ and a further localization if necessary, we obtain a tower
$({\tilde{Y}},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$ and a further localization if necessary, we obtain a tower
 $$\begin{eqnarray}{\tilde{Y}}\simeq Y_{n}\rightarrow \cdots \rightarrow Y_{1}\rightarrow Y_{0}\rightarrow Y,\end{eqnarray}$$
$$\begin{eqnarray}{\tilde{Y}}\simeq Y_{n}\rightarrow \cdots \rightarrow Y_{1}\rightarrow Y_{0}\rightarrow Y,\end{eqnarray}$$ with  $(Y_{0},{\rm\Sigma}_{0})\rightarrow (Y,{\it\sigma})$ finite Galois and all
$(Y_{0},{\rm\Sigma}_{0})\rightarrow (Y,{\it\sigma})$ finite Galois and all  $Y_{i+1}\rightarrow Y_{i}$ proper benign, for
$Y_{i+1}\rightarrow Y_{i}$ proper benign, for ![]() $i\geqslant 0$. In the effective case, all this can be achieved in a
$i\geqslant 0$. In the effective case, all this can be achieved in a ![]() $\dagger$-primitive recursive way, using (†6), (†4), (†5). The first morphism is a Galois cover and therefore surjective by 2.22 and its generalizations, and proper benign morphisms are clearly surjective. Thus, we conclude that
$\dagger$-primitive recursive way, using (†6), (†4), (†5). The first morphism is a Galois cover and therefore surjective by 2.22 and its generalizations, and proper benign morphisms are clearly surjective. Thus, we conclude that ![]() $f$ can be made surjective upon a finite
$f$ can be made surjective upon a finite ![]() ${\it\sigma}$-localization, which is enough to deduce the required statement.◻
${\it\sigma}$-localization, which is enough to deduce the required statement.◻
Definition 7.8. Let ![]() $(S,{\it\sigma})$ be a normal integral difference scheme of finite
$(S,{\it\sigma})$ be a normal integral difference scheme of finite ![]() ${\it\sigma}$-type over
${\it\sigma}$-type over ![]() $\mathbb{Z}$, and let
$\mathbb{Z}$, and let ![]() $(X,{\it\sigma})$ be an
$(X,{\it\sigma})$ be an ![]() $(S,{\it\sigma})$-difference scheme. Let
$(S,{\it\sigma})$-difference scheme. Let ![]() ${\mathcal{F}}$ and
${\mathcal{F}}$ and ![]() ${\mathcal{F}}^{\prime }$ be
${\mathcal{F}}^{\prime }$ be ![]() $(S,{\it\sigma})$-subassignments of
$(S,{\it\sigma})$-subassignments of ![]() $X$ and let
$X$ and let ![]() $m$ be a positive integer. We shall write
$m$ be a positive integer. We shall write
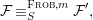 $$\begin{eqnarray}{\mathcal{F}}\equiv _{S}^{{\rm \small{Frob}},m}{\mathcal{F}}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}\equiv _{S}^{{\rm \small{Frob}},m}{\mathcal{F}}^{\prime },\end{eqnarray}$$ if for every closed ![]() $s\in S$, every finite field
$s\in S$, every finite field ![]() $k$ with
$k$ with ![]() $(\bar{k},{\it\varphi}_{k})$ extending
$(\bar{k},{\it\varphi}_{k})$ extending 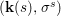 $(\mathbf{k}(s),{\it\sigma}^{s})$ and
$(\mathbf{k}(s),{\it\sigma}^{s})$ and ![]() $|k|\geqslant m$,
$|k|\geqslant m$,
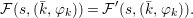 $$\begin{eqnarray}{\mathcal{F}}(s,(\bar{k},{\it\varphi}_{k}))={\mathcal{F}}^{\prime }(s,(\bar{k},{\it\varphi}_{k})).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}(s,(\bar{k},{\it\varphi}_{k}))={\mathcal{F}}^{\prime }(s,(\bar{k},{\it\varphi}_{k})).\end{eqnarray}$$ We say that ![]() ${\mathcal{F}}$ and
${\mathcal{F}}$ and ![]() ${\mathcal{F}}^{\prime }$ are equivalent modulo fields with Frobenii over
${\mathcal{F}}^{\prime }$ are equivalent modulo fields with Frobenii over ![]() $S$ and write
$S$ and write
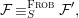 $$\begin{eqnarray}{\mathcal{F}}\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{F}}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{F}}^{\prime },\end{eqnarray}$$ if 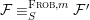 ${\mathcal{F}}\equiv _{S}^{{\rm \small{Frob}},m}{\mathcal{F}}^{\prime }$ for some
${\mathcal{F}}\equiv _{S}^{{\rm \small{Frob}},m}{\mathcal{F}}^{\prime }$ for some ![]() $m$. We write
$m$. We write 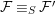 ${\mathcal{F}}\equiv _{S}{\mathcal{F}}^{\prime }$, if the two subassignments agree over all algebraically closed difference fields.
${\mathcal{F}}\equiv _{S}{\mathcal{F}}^{\prime }$, if the two subassignments agree over all algebraically closed difference fields.
Definition 7.9. Let 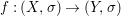 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of ![]() $(S,{\it\sigma})$-difference schemes and let
$(S,{\it\sigma})$-difference schemes and let ![]() ${\mathcal{A}}$ be Galois stratification on
${\mathcal{A}}$ be Galois stratification on ![]() $X$. For
$X$. For ![]() $s\in S$ and
$s\in S$ and ![]() $(F,{\it\varphi})$ an algebraically closed difference field extending
$(F,{\it\varphi})$ an algebraically closed difference field extending 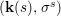 $(\mathbf{k}(s),{\it\sigma}^{s})$, we define a subassignment
$(\mathbf{k}(s),{\it\sigma}^{s})$, we define a subassignment ![]() $f_{\exists }{\mathcal{A}}$ of
$f_{\exists }{\mathcal{A}}$ of ![]() $Y$ by the rule
$Y$ by the rule
 $$\begin{eqnarray}f_{\exists }{\mathcal{A}}(s,(F,{\it\varphi}))=(f_{\exists }{\mathcal{A}})_{s}(F,{\it\varphi})=f_{s}({\mathcal{A}}_{s}(F,{\it\varphi}))\subseteq Y_{s}(F,{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }{\mathcal{A}}(s,(F,{\it\varphi}))=(f_{\exists }{\mathcal{A}})_{s}(F,{\it\varphi})=f_{s}({\mathcal{A}}_{s}(F,{\it\varphi}))\subseteq Y_{s}(F,{\it\varphi}).\end{eqnarray}$$ When ![]() ${\mathcal{A}}$ is associated with a Galois formula
${\mathcal{A}}$ is associated with a Galois formula 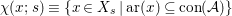 ${\it\chi}(x;s)\equiv \{x\in X_{s}\mid \text{ar}(x)\subseteq \text{con}({\mathcal{A}})\}$, it can be identified with an expression
${\it\chi}(x;s)\equiv \{x\in X_{s}\mid \text{ar}(x)\subseteq \text{con}({\mathcal{A}})\}$, it can be identified with an expression
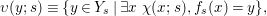 $$\begin{eqnarray}{\it\upsilon}(y;s)\equiv \{y\in Y_{s}\mid \exists x~{\it\chi}(x;s),f_{s}(x)=y\},\end{eqnarray}$$
$$\begin{eqnarray}{\it\upsilon}(y;s)\equiv \{y\in Y_{s}\mid \exists x~{\it\chi}(x;s),f_{s}(x)=y\},\end{eqnarray}$$which justifies the notation somewhat.
Lemma 7.10. Suppose that
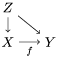
is a triangle of étale Galois covers. We have an exact sequence of groups with operators
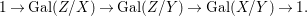 $$\begin{eqnarray}1\rightarrow \text{Gal}(Z/X)\rightarrow \text{Gal}(Z/Y)\rightarrow \text{Gal}(X/Y)\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \text{Gal}(Z/X)\rightarrow \text{Gal}(Z/Y)\rightarrow \text{Gal}(X/Y)\rightarrow 1.\end{eqnarray}$$ Let 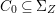 $C_{0}\subseteq {\rm\Sigma}_{Z}$ be a
$C_{0}\subseteq {\rm\Sigma}_{Z}$ be a 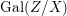 $\text{Gal}(Z/X)$-conjugacy domain, and let
$\text{Gal}(Z/X)$-conjugacy domain, and let ![]() $C$ be the
$C$ be the 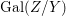 $\text{Gal}(Z/Y)$-conjugacy domain induced by
$\text{Gal}(Z/Y)$-conjugacy domain induced by ![]() $C_{0}$. Then
$C_{0}$. Then
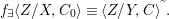 $$\begin{eqnarray}f_{\exists }\langle Z/X,C_{0}\rangle \equiv \langle Z/Y,C\rangle ^{\widetilde{~}}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }\langle Z/X,C_{0}\rangle \equiv \langle Z/Y,C\rangle ^{\widetilde{~}}.\end{eqnarray}$$Proof. For the nontrivial inclusion, let ![]() $(F,{\it\varphi})$ be an arbitrary algebraically closed difference field containing the field of definition of
$(F,{\it\varphi})$ be an arbitrary algebraically closed difference field containing the field of definition of ![]() $Y$, and suppose
$Y$, and suppose 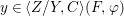 $y\in \langle Z/Y,C\rangle (F,{\it\varphi})$. There exists a
$y\in \langle Z/Y,C\rangle (F,{\it\varphi})$. There exists a 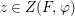 $z\in Z(F,{\it\varphi})$ such that
$z\in Z(F,{\it\varphi})$ such that ![]() $z\mapsto y$ and
$z\mapsto y$ and
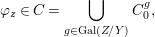 $$\begin{eqnarray}{\it\varphi}_{z}\in C=\mathop{\bigcup }_{g\in \text{Gal}(Z/Y)}C_{0}^{g},\end{eqnarray}$$
$$\begin{eqnarray}{\it\varphi}_{z}\in C=\mathop{\bigcup }_{g\in \text{Gal}(Z/Y)}C_{0}^{g},\end{eqnarray}$$ so let 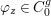 ${\it\varphi}_{z}\in C_{0}^{g}$. Then
${\it\varphi}_{z}\in C_{0}^{g}$. Then 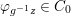 ${\it\varphi}_{g^{-1}z}\in C_{0}$, so the image
${\it\varphi}_{g^{-1}z}\in C_{0}$, so the image ![]() $x$ of
$x$ of ![]() $g^{-1}z$ in
$g^{-1}z$ in ![]() $X$ witnesses
$X$ witnesses 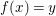 $f(x)=y$ and
$f(x)=y$ and 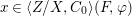 $x\in \langle Z/X,C_{0}\rangle (F,{\it\varphi})$.◻
$x\in \langle Z/X,C_{0}\rangle (F,{\it\varphi})$.◻
Lemma 7.11. Let 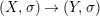 $(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a finite étale morphism of normal difference schemes, let
$(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a finite étale morphism of normal difference schemes, let 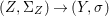 $(Z,{\rm\Sigma}_{Z})\rightarrow (Y,{\it\sigma})$ be a Galois cover, and let
$(Z,{\rm\Sigma}_{Z})\rightarrow (Y,{\it\sigma})$ be a Galois cover, and let 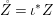 $\mathring{Z}={\it\iota}^{\ast }Z$ be a difference scheme obtained by restricting the difference structure via some
$\mathring{Z}={\it\iota}^{\ast }Z$ be a difference scheme obtained by restricting the difference structure via some 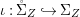 ${\it\iota}:\mathring{\Sigma}_{Z}{\hookrightarrow}{\rm\Sigma}_{Z}$ so that
${\it\iota}:\mathring{\Sigma}_{Z}{\hookrightarrow}{\rm\Sigma}_{Z}$ so that ![]() $\mathring{Z}\rightarrow X$ is a Galois cover. Let
$\mathring{Z}\rightarrow X$ is a Galois cover. Let ![]() $C$ be a
$C$ be a 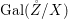 $\text{Gal}(\mathring{Z}/X)$-conjugacy class in
$\text{Gal}(\mathring{Z}/X)$-conjugacy class in ![]() $\mathring{\Sigma}_{Z}$. Then
$\mathring{\Sigma}_{Z}$. Then
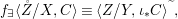 $$\begin{eqnarray}f_{\exists }\langle \mathring{Z}/X,C\rangle \equiv \langle Z/Y,{\it\iota}_{\ast }C\rangle ^{\widetilde{~}},\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }\langle \mathring{Z}/X,C\rangle \equiv \langle Z/Y,{\it\iota}_{\ast }C\rangle ^{\widetilde{~}},\end{eqnarray}$$ where ![]() ${\it\iota}_{\ast }C$ is the smallest
${\it\iota}_{\ast }C$ is the smallest 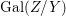 $\text{Gal}(Z/Y)$-conjugacy domain in
$\text{Gal}(Z/Y)$-conjugacy domain in ![]() ${\rm\Sigma}_{Z}$ containing
${\rm\Sigma}_{Z}$ containing ![]() ${\it\iota}(C)$.
${\it\iota}(C)$.
Proof. The diagram
shows the situation following the insertion of the Galois closure of ![]() $X$ over
$X$ over ![]() $Y$. Starting with a
$Y$. Starting with a 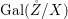 $\text{Gal}(\mathring{Z}/X)$-conjugacy class
$\text{Gal}(\mathring{Z}/X)$-conjugacy class ![]() $C$ in
$C$ in ![]() $\mathring{\Sigma}_{Z}$, we can consider it as a
$\mathring{\Sigma}_{Z}$, we can consider it as a 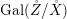 $\text{Gal}(\mathring{Z}/\mathring{X})$-conjugacy domain
$\text{Gal}(\mathring{Z}/\mathring{X})$-conjugacy domain ![]() $C^{\prime }$, and write
$C^{\prime }$, and write ![]() $C^{\prime \prime }$ for
$C^{\prime \prime }$ for ![]() $C^{\prime }$ considered in
$C^{\prime }$ considered in ![]() $Z/\tilde{X}$, so that
$Z/\tilde{X}$, so that 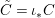 $\tilde{C}={\it\iota}_{\ast }C$ is the
$\tilde{C}={\it\iota}_{\ast }C$ is the 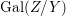 $\text{Gal}(Z/Y)$-conjugacy domain induced by
$\text{Gal}(Z/Y)$-conjugacy domain induced by ![]() $C^{\prime \prime }$. Using 7.10, we have that
$C^{\prime \prime }$. Using 7.10, we have that 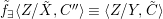 $\tilde{f}_{\exists }\langle Z/\tilde{X},C^{\prime \prime }\rangle \equiv \langle Z/Y,\tilde{C}\rangle$ and
$\tilde{f}_{\exists }\langle Z/\tilde{X},C^{\prime \prime }\rangle \equiv \langle Z/Y,\tilde{C}\rangle$ and 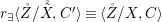 $r_{\exists }\langle \mathring{Z}/\mathring{\tilde{X}},C^{\prime }\rangle \equiv \langle \mathring{Z}/X,C\rangle$. Thus
$r_{\exists }\langle \mathring{Z}/\mathring{\tilde{X}},C^{\prime }\rangle \equiv \langle \mathring{Z}/X,C\rangle$. Thus
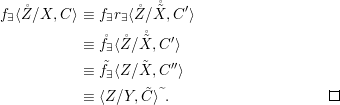 $$\begin{eqnarray}\displaystyle f_{\exists }\langle \mathring{Z}/X,C\rangle & \equiv & \displaystyle f_{\exists }r_{\exists }\langle \mathring{Z}/\mathring{\tilde{X}},C^{\prime }\rangle \nonumber\\ \displaystyle & \equiv & \displaystyle \mathring{f}_{\exists }\langle \mathring{Z}/\mathring{\tilde{X}},C^{\prime }\rangle \nonumber\\ \displaystyle & \equiv & \displaystyle \tilde{f}_{\exists }\langle Z/\tilde{X},C^{\prime \prime }\rangle \nonumber\\ \displaystyle & \equiv & \displaystyle \langle Z/Y,\tilde{C}\rangle ^{\widetilde{~}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{\exists }\langle \mathring{Z}/X,C\rangle & \equiv & \displaystyle f_{\exists }r_{\exists }\langle \mathring{Z}/\mathring{\tilde{X}},C^{\prime }\rangle \nonumber\\ \displaystyle & \equiv & \displaystyle \mathring{f}_{\exists }\langle \mathring{Z}/\mathring{\tilde{X}},C^{\prime }\rangle \nonumber\\ \displaystyle & \equiv & \displaystyle \tilde{f}_{\exists }\langle Z/\tilde{X},C^{\prime \prime }\rangle \nonumber\\ \displaystyle & \equiv & \displaystyle \langle Z/Y,\tilde{C}\rangle ^{\widetilde{~}}.\nonumber\end{eqnarray}$$ The main result of this paper is the following direct image theorem, stating that the class of Galois formulas over fields with Frobenii is closed under taking images by ![]() $f_{\exists }$.
$f_{\exists }$.
Theorem 7.12. Let ![]() $(S,{\it\sigma})$ be a difference scheme of finite
$(S,{\it\sigma})$ be a difference scheme of finite ![]() ${\it\sigma}$-type over
${\it\sigma}$-type over ![]() $\mathbb{Z}$ and let
$\mathbb{Z}$ and let 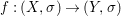 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ be a morphism of ![]() $(S,{\it\sigma})$-difference schemes of finite
$(S,{\it\sigma})$-difference schemes of finite ![]() ${\it\sigma}$-type. For every Galois formula
${\it\sigma}$-type. For every Galois formula ![]() ${\mathcal{A}}$ of
${\mathcal{A}}$ of ![]() $X$, the subassignment
$X$, the subassignment ![]() $f_{\exists }{\mathcal{A}}$ is
$f_{\exists }{\mathcal{A}}$ is ![]() $\equiv _{S}^{{\rm \small{Frob}}}$-equivalent to a Galois formula on
$\equiv _{S}^{{\rm \small{Frob}}}$-equivalent to a Galois formula on ![]() $Y$, that is, there exists a Galois formula
$Y$, that is, there exists a Galois formula ![]() ${\mathcal{B}}$ on
${\mathcal{B}}$ on ![]() $Y$ such that
$Y$ such that
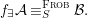 $$\begin{eqnarray}f_{\exists }{\mathcal{A}}\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{B}}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }{\mathcal{A}}\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{B}}.\end{eqnarray}$$ When ![]() ${\mathcal{A}}$ is effectively given, a
${\mathcal{A}}$ is effectively given, a ![]() $\dagger$-primitive recursive procedure yields an effectively given
$\dagger$-primitive recursive procedure yields an effectively given ![]() ${\mathcal{B}}$ and a constant
${\mathcal{B}}$ and a constant ![]() $m>0$ such that
$m>0$ such that
 $$\begin{eqnarray}f_{\exists }{\mathcal{A}}\equiv _{S}^{{\rm \small{Frob}},m}{\mathcal{B}}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }{\mathcal{A}}\equiv _{S}^{{\rm \small{Frob}},m}{\mathcal{B}}.\end{eqnarray}$$Proof. The proof is by devissage, or Noetherian induction, whereby in each step we calculate the direct image on a dense open piece and postpone the calculation on the “bad locus” complement to the next step. At the end of the procedure, we have obtained the image of each piece of the domain as a Galois stratification supported on a locally closed piece of the codomain. To finish, we extend all of these trivially to produce Galois formulas on the whole of ![]() $Y$, and we take their disjunction to represent the total image as a Galois formula.
$Y$, and we take their disjunction to represent the total image as a Galois formula.
In order to show that the procedure is ![]() $\dagger$-primitive recursive in the effective case, we must argue that our Noetherian induction procedure can be rewritten in terms of bounded loops. This is a consequence of the fact that our devissage is controlled (unlike arbitrary Noetherian induction algorithms, which are notoriously far from being primitive recursive). Indeed, in each step the “lower-dimensional bad locus” can be computed explicitly and its degree/complexity can be bounded, and, even though the number of its components may be very large, it can be computed by the
$\dagger$-primitive recursive in the effective case, we must argue that our Noetherian induction procedure can be rewritten in terms of bounded loops. This is a consequence of the fact that our devissage is controlled (unlike arbitrary Noetherian induction algorithms, which are notoriously far from being primitive recursive). Indeed, in each step the “lower-dimensional bad locus” can be computed explicitly and its degree/complexity can be bounded, and, even though the number of its components may be very large, it can be computed by the ![]() $\dagger$-oracles such as (†1). Thus, even though the algorithm is written down as a devissage argument for convenience, the main control loop can in fact be bounded.
$\dagger$-oracles such as (†1). Thus, even though the algorithm is written down as a devissage argument for convenience, the main control loop can in fact be bounded.
Given that we are interested in points with values in difference fields, we may assume that ![]() $X$ and
$X$ and ![]() $Y$ are perfectly reduced, so we can decompose them into transformally integral components using (†1), and we can thus reduce to the case where
$Y$ are perfectly reduced, so we can decompose them into transformally integral components using (†1), and we can thus reduce to the case where ![]() $X$ and
$X$ and ![]() $Y$ are transformally integral.
$Y$ are transformally integral.
By splitting off the radicial and ![]() ${\it\sigma}$-radicial part as in the proof of 7.7, we may assume that
${\it\sigma}$-radicial part as in the proof of 7.7, we may assume that ![]() $f$ is separable
$f$ is separable ![]() ${\it\sigma}$-separable. In the effective case, we use (†3).
${\it\sigma}$-separable. In the effective case, we use (†3).
Thus, by a Noetherian induction trick using generic ![]() ${\it\sigma}$-pro-smoothness 3.8 and 7.7, after a possible refinement of
${\it\sigma}$-pro-smoothness 3.8 and 7.7, after a possible refinement of ![]() ${\mathcal{A}}$, we obtain stratifications
${\mathcal{A}}$, we obtain stratifications ![]() $X_{i}$ and
$X_{i}$ and ![]() $Y_{j}$ into transformally integral normal locally closed
$Y_{j}$ into transformally integral normal locally closed ![]() $(S,{\it\sigma})$-subschemes of
$(S,{\it\sigma})$-subschemes of ![]() $X$ and
$X$ and ![]() $Y$ such that for every
$Y$ such that for every ![]() $i$ there exists a
$i$ there exists a ![]() $j$ with
$j$ with 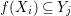 $f(X_{i})\subseteq Y_{j}$ and
$f(X_{i})\subseteq Y_{j}$ and 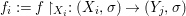 $f_{i}:=f\restriction_{X_{i}}:(X_{i},{\it\sigma})\rightarrow (Y_{j},{\it\sigma})$ is
$f_{i}:=f\restriction_{X_{i}}:(X_{i},{\it\sigma})\rightarrow (Y_{j},{\it\sigma})$ is ![]() ${\it\sigma}$-pro-smooth
${\it\sigma}$-pro-smooth ![]() ${\it\sigma}$-separable. This can be done in a
${\it\sigma}$-separable. This can be done in a ![]() $\dagger$-primitive recursive way, using (†6) and the effective case of 7.7.
$\dagger$-primitive recursive way, using (†6) and the effective case of 7.7.
By the philosophy of the proof, we can restrict our attention to one of the ![]() $f_{i}$, so we disregard the index
$f_{i}$, so we disregard the index ![]() $i$ and write
$i$ and write 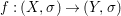 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ in place of
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ in place of ![]() $f_{i}$, and we may assume that
$f_{i}$, and we may assume that ![]() ${\mathcal{A}}$ on
${\mathcal{A}}$ on ![]() $X$ is basic,
$X$ is basic, 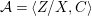 ${\mathcal{A}}=\langle Z/X,C\rangle$, where
${\mathcal{A}}=\langle Z/X,C\rangle$, where 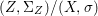 $(Z,{\rm\Sigma}_{Z})/(X,{\it\sigma})$ is a transformally integral Galois cover with group
$(Z,{\rm\Sigma}_{Z})/(X,{\it\sigma})$ is a transformally integral Galois cover with group  $(G,\tilde{{\rm\Sigma}}_{Z})$ and
$(G,\tilde{{\rm\Sigma}}_{Z})$ and ![]() $C$ is a
$C$ is a ![]() $G$-conjugacy domain in
$G$-conjugacy domain in ![]() ${\rm\Sigma}_{Z}$.
${\rm\Sigma}_{Z}$.
By considering the normalization ![]() ${\tilde{Y}}$ in the relative algebraic closure of
${\tilde{Y}}$ in the relative algebraic closure of ![]() $\mathbf{k}(Y)$ inside
$\mathbf{k}(Y)$ inside ![]() $\mathbf{k}(X)$, we obtain a baby Stein factorization
$\mathbf{k}(X)$, we obtain a baby Stein factorization 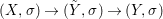 $(X,{\it\sigma})\rightarrow ({\tilde{Y}},{\it\sigma})\rightarrow (Y,{\it\sigma})$, where the first morphism has generically geometrically transformally integral fibers (by 3.50), and the second is generically
$(X,{\it\sigma})\rightarrow ({\tilde{Y}},{\it\sigma})\rightarrow (Y,{\it\sigma})$, where the first morphism has generically geometrically transformally integral fibers (by 3.50), and the second is generically ![]() ${\it\sigma}$-pro-étale
${\it\sigma}$-pro-étale ![]() ${\it\sigma}$-separable. In the effective situation, this requires (†2).
${\it\sigma}$-separable. In the effective situation, this requires (†2).
Thus, we can split our considerations into two cases.
Case 1. We have a morphism 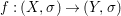 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ of transformally integral
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ of transformally integral ![]() $(S,{\it\sigma})$-schemes whose generic fiber is geometrically transformally integral, and
$(S,{\it\sigma})$-schemes whose generic fiber is geometrically transformally integral, and 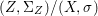 $(Z,{\rm\Sigma}_{Z})/(X,{\it\sigma})$ is étale Galois with
$(Z,{\rm\Sigma}_{Z})/(X,{\it\sigma})$ is étale Galois with ![]() $Z$ transformally integral.
$Z$ transformally integral.
Let 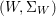 $(W,{\rm\Sigma}_{W})$ be the normalization of
$(W,{\rm\Sigma}_{W})$ be the normalization of ![]() $(Y,{\it\sigma})$ in the relative algebraic closure of
$(Y,{\it\sigma})$ in the relative algebraic closure of ![]() $\mathbf{k}(Y)$ in
$\mathbf{k}(Y)$ in 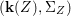 $(\mathbf{k}(Z),{\rm\Sigma}_{Z})$, in the effective case calculated by (†2) and (†5). Then
$(\mathbf{k}(Z),{\rm\Sigma}_{Z})$, in the effective case calculated by (†2) and (†5). Then 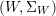 $(W,{\rm\Sigma}_{W})$ is a Galois cover of
$(W,{\rm\Sigma}_{W})$ is a Galois cover of ![]() $(Y,{\it\sigma})$. Writing
$(Y,{\it\sigma})$. Writing 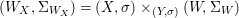 $(W_{X},{\rm\Sigma}_{W_{X}})=(X,{\it\sigma})\times _{(Y,{\it\sigma})}(W,{\rm\Sigma}_{W})$, we obtain an exact sequence
$(W_{X},{\rm\Sigma}_{W_{X}})=(X,{\it\sigma})\times _{(Y,{\it\sigma})}(W,{\rm\Sigma}_{W})$, we obtain an exact sequence
 $$\begin{eqnarray}1\rightarrow \text{Gal}(Z/W_{X})\rightarrow \text{Gal}(Z/X)\rightarrow \text{Gal}(W/Y)\rightarrow 1,\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow \text{Gal}(Z/W_{X})\rightarrow \text{Gal}(Z/X)\rightarrow \text{Gal}(W/Y)\rightarrow 1,\end{eqnarray}$$ together with a ![]() $\mathit{Diff}$-quotient morphism
$\mathit{Diff}$-quotient morphism
 $$\begin{eqnarray}{\it\pi}:{\rm\Sigma}_{Z}\rightarrow {\rm\Sigma}_{Z}/\text{Gal}(Z/W_{X})={\rm\Sigma}_{W}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}:{\rm\Sigma}_{Z}\rightarrow {\rm\Sigma}_{Z}/\text{Gal}(Z/W_{X})={\rm\Sigma}_{W}.\end{eqnarray}$$ By a ![]() ${\it\sigma}$-localization, using 3.14 and 3.15, we may assume that
${\it\sigma}$-localization, using 3.14 and 3.15, we may assume that
(i)
 $W$ is transformally integral and
$W$ is transformally integral and  $(W,{\rm\Sigma}_{W})/(Y,{\it\sigma})$ is étale Galois;
$(W,{\rm\Sigma}_{W})/(Y,{\it\sigma})$ is étale Galois;(ii)
 $f$ and
$f$ and  $Z\rightarrow W$ (and consequently
$Z\rightarrow W$ (and consequently  $W_{X}\rightarrow W$) have directly geometrically transformally integral fibers;
$W_{X}\rightarrow W$) have directly geometrically transformally integral fibers;(iii)
 $\text{Gal}(Z_{w}/W_{w})=\text{Gal}(Z/W_{X})$ for all fibers
$\text{Gal}(Z_{w}/W_{w})=\text{Gal}(Z/W_{X})$ for all fibers  $Z_{w}$ of
$Z_{w}$ of  $Z\rightarrow W$ and
$Z\rightarrow W$ and  $W_{w}$ of
$W_{w}$ of  $W_{X}\rightarrow W$ above
$W_{X}\rightarrow W$ above  $w\in W$.
$w\in W$.
This is effective by (†5), (†6) and (†8).
Let 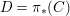 $D={\it\pi}_{\ast }(C)$ be the image of
$D={\it\pi}_{\ast }(C)$ be the image of ![]() $C$ in
$C$ in ![]() ${\rm\Sigma}_{W}$, computed by (†8), and we claim that
${\rm\Sigma}_{W}$, computed by (†8), and we claim that
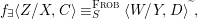 $$\begin{eqnarray}f_{\exists }\langle Z/X,C\rangle \equiv _{S}^{{\rm \small{Frob}}}\langle W/Y,D\rangle ^{\widetilde{~}},\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }\langle Z/X,C\rangle \equiv _{S}^{{\rm \small{Frob}}}\langle W/Y,D\rangle ^{\widetilde{~}},\end{eqnarray}$$ that is, for all closed ![]() $s\in S$, all large enough
$s\in S$, all large enough ![]() $k$ with
$k$ with ![]() $(\bar{k},{\it\varphi}_{k})$ extending
$(\bar{k},{\it\varphi}_{k})$ extending 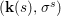 $(\mathbf{k}(s),{\it\sigma}^{s})$,
$(\mathbf{k}(s),{\it\sigma}^{s})$,
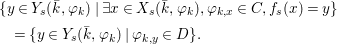 $$\begin{eqnarray}\displaystyle & & \displaystyle \{y\in Y_{s}(\bar{k},{\it\varphi}_{k})\mid \exists x\in X_{s}(\bar{k},{\it\varphi}_{k}),{\it\varphi}_{k,x}\in C,f_{s}(x)=y\}\nonumber\\ \displaystyle & & \displaystyle \quad =\{y\in Y_{s}(\bar{k},{\it\varphi}_{k})\mid {\it\varphi}_{k,y}\in D\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \{y\in Y_{s}(\bar{k},{\it\varphi}_{k})\mid \exists x\in X_{s}(\bar{k},{\it\varphi}_{k}),{\it\varphi}_{k,x}\in C,f_{s}(x)=y\}\nonumber\\ \displaystyle & & \displaystyle \quad =\{y\in Y_{s}(\bar{k},{\it\varphi}_{k})\mid {\it\varphi}_{k,y}\in D\}.\end{eqnarray}$$ A routine verification of the left to right inclusion needs no assumptions on the size of ![]() $k$. Conversely, let
$k$. Conversely, let 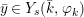 $\bar{y}\in Y_{s}(\bar{k},{\it\varphi}_{k})$,
$\bar{y}\in Y_{s}(\bar{k},{\it\varphi}_{k})$, 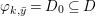 ${\it\varphi}_{k,\bar{y}}=D_{0}\subseteq D$. Pick some
${\it\varphi}_{k,\bar{y}}=D_{0}\subseteq D$. Pick some ![]() $\bar{y}^{\prime }$ in the fiber of
$\bar{y}^{\prime }$ in the fiber of ![]() $W/Y$ above
$W/Y$ above ![]() $\bar{y}$ with
$\bar{y}$ with 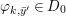 ${\it\varphi}_{k,\bar{y}^{\prime }}\in D_{0}$. Let us denote by
${\it\varphi}_{k,\bar{y}^{\prime }}\in D_{0}$. Let us denote by ![]() $y\in Y_{s}$ and
$y\in Y_{s}$ and ![]() $y^{\prime }\in W_{s}$ the loci of
$y^{\prime }\in W_{s}$ the loci of ![]() $\bar{y}$ and
$\bar{y}$ and ![]() $\bar{y}^{\prime }$,
$\bar{y}^{\prime }$, 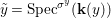 ${\tilde{y}}=\text{Spec}^{{\it\sigma}^{y}}(\mathbf{k}(y))$,
${\tilde{y}}=\text{Spec}^{{\it\sigma}^{y}}(\mathbf{k}(y))$, 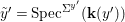 ${\tilde{y}}^{\prime }=\text{Spec}^{{\rm\Sigma}^{y^{\prime }}}(\mathbf{k}(y^{\prime }))$ (where
${\tilde{y}}^{\prime }=\text{Spec}^{{\rm\Sigma}^{y^{\prime }}}(\mathbf{k}(y^{\prime }))$ (where ![]() ${\rm\Sigma}^{y^{\prime }}$ is shorthand for
${\rm\Sigma}^{y^{\prime }}$ is shorthand for ![]() ${\rm\Sigma}_{W}^{y^{\prime }}$) and consider the diagram
${\rm\Sigma}_{W}^{y^{\prime }}$) and consider the diagram
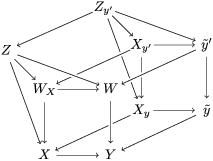
where 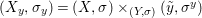 $(X_{y},{\it\sigma}_{y})=(X,{\it\sigma})\times _{(Y,{\it\sigma})}({\tilde{y}},{\it\sigma}^{y})$ is the fiber of
$(X_{y},{\it\sigma}_{y})=(X,{\it\sigma})\times _{(Y,{\it\sigma})}({\tilde{y}},{\it\sigma}^{y})$ is the fiber of ![]() $X$ above
$X$ above ![]() $y$,
$y$, 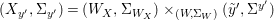 $(X_{y^{\prime }},{\rm\Sigma}_{y^{\prime }})=(W_{X},{\rm\Sigma}_{W_{X}})\times _{(W,{\rm\Sigma}_{W})}({\tilde{y}}^{\prime },{\rm\Sigma}^{y^{\prime }})$ is the fiber of
$(X_{y^{\prime }},{\rm\Sigma}_{y^{\prime }})=(W_{X},{\rm\Sigma}_{W_{X}})\times _{(W,{\rm\Sigma}_{W})}({\tilde{y}}^{\prime },{\rm\Sigma}^{y^{\prime }})$ is the fiber of ![]() $W_{X}$ above
$W_{X}$ above ![]() $y^{\prime }$, and
$y^{\prime }$, and
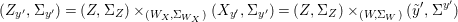 $$\begin{eqnarray}(Z_{y^{\prime }},{\rm\Sigma}_{y^{\prime }})=(Z,{\rm\Sigma}_{Z})\times _{(W_{X},{\rm\Sigma}_{W_{X}})}(X_{y^{\prime }},{\rm\Sigma}_{y^{\prime }})=(Z,{\rm\Sigma}_{Z})\times _{(W,{\rm\Sigma}_{W})}({\tilde{y}}^{\prime },{\rm\Sigma}^{y^{\prime }})\end{eqnarray}$$
$$\begin{eqnarray}(Z_{y^{\prime }},{\rm\Sigma}_{y^{\prime }})=(Z,{\rm\Sigma}_{Z})\times _{(W_{X},{\rm\Sigma}_{W_{X}})}(X_{y^{\prime }},{\rm\Sigma}_{y^{\prime }})=(Z,{\rm\Sigma}_{Z})\times _{(W,{\rm\Sigma}_{W})}({\tilde{y}}^{\prime },{\rm\Sigma}^{y^{\prime }})\end{eqnarray}$$ is the fiber of ![]() $Z$ above
$Z$ above ![]() $y^{\prime }$. By construction,
$y^{\prime }$. By construction, ![]() $Z_{y^{\prime }}$ is directly geometrically transformally integral and
$Z_{y^{\prime }}$ is directly geometrically transformally integral and 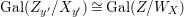 $\text{Gal}(Z_{y^{\prime }}/X_{y^{\prime }})\cong \text{Gal}(Z/W_{X})$. In the diagram with exact rows
$\text{Gal}(Z_{y^{\prime }}/X_{y^{\prime }})\cong \text{Gal}(Z/W_{X})$. In the diagram with exact rows
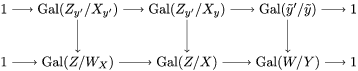
the left vertical arrow is an isomorphism and 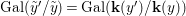 $\text{Gal}({\tilde{y}}^{\prime }/{\tilde{y}})=\text{Gal}(\mathbf{k}(y^{\prime })/\mathbf{k}(y))$. It follows that
$\text{Gal}({\tilde{y}}^{\prime }/{\tilde{y}})=\text{Gal}(\mathbf{k}(y^{\prime })/\mathbf{k}(y))$. It follows that 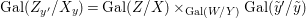 $\text{Gal}(Z_{y^{\prime }}/X_{y})=\text{Gal}(Z/X)\times _{\text{Gal}(W/Y)}\text{Gal}({\tilde{y}}^{\prime }/{\tilde{y}})$ and we get a Cartesian diagram of difference structures:
$\text{Gal}(Z_{y^{\prime }}/X_{y})=\text{Gal}(Z/X)\times _{\text{Gal}(W/Y)}\text{Gal}({\tilde{y}}^{\prime }/{\tilde{y}})$ and we get a Cartesian diagram of difference structures:
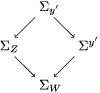
Thus we can find a conjugacy domain 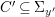 $C^{\prime }\subseteq {\rm\Sigma}_{y^{\prime }}$ which maps into
$C^{\prime }\subseteq {\rm\Sigma}_{y^{\prime }}$ which maps into ![]() $C$ in
$C$ in ![]() ${\rm\Sigma}_{Z}$ (and eventually to
${\rm\Sigma}_{Z}$ (and eventually to 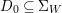 $D_{0}\subseteq {\rm\Sigma}_{W}$), as well as onto
$D_{0}\subseteq {\rm\Sigma}_{W}$), as well as onto ![]() ${\it\varphi}_{k}$. It suffices to find an
${\it\varphi}_{k}$. It suffices to find an 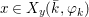 $x\in X_{y}(\bar{k},{\it\varphi}_{k})$ with
$x\in X_{y}(\bar{k},{\it\varphi}_{k})$ with 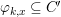 ${\it\varphi}_{k,x}\subseteq C^{\prime }$ with respect to the cover
${\it\varphi}_{k,x}\subseteq C^{\prime }$ with respect to the cover ![]() $Z_{y^{\prime }}/X_{y}$, and this is possible for large enough
$Z_{y^{\prime }}/X_{y}$, and this is possible for large enough ![]() $k$ by Twisted Chebotarev [Reference Tomašić24, 4.28]. The relevant bound for the size of
$k$ by Twisted Chebotarev [Reference Tomašić24, 4.28]. The relevant bound for the size of ![]() $k$ can be calculated by (†9).
$k$ can be calculated by (†9).
Case 2. The morphism 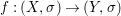 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is generically
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is generically ![]() ${\it\sigma}$-pro-étale
${\it\sigma}$-pro-étale ![]() ${\it\sigma}$-separable of transformally integral
${\it\sigma}$-separable of transformally integral ![]() $(S,{\it\sigma})$-schemes.
$(S,{\it\sigma})$-schemes.
Using 5.24, the generic weak Galois closure of ![]() $X$ over
$X$ over ![]() $Y$ consists of generic weak covers
$Y$ consists of generic weak covers 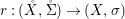 $r:(\mathring{X},\mathring{\Sigma})\rightarrow (X,{\it\sigma})$ and
$r:(\mathring{X},\mathring{\Sigma})\rightarrow (X,{\it\sigma})$ and ![]() $\tilde{X}\rightarrow Y$ such that
$\tilde{X}\rightarrow Y$ such that 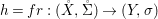 $h=fr:(\mathring{X},\mathring{\Sigma})\rightarrow (Y,{\it\sigma})$ is quasi-Galois. By 3.8 and 7.7, modulo a
$h=fr:(\mathring{X},\mathring{\Sigma})\rightarrow (Y,{\it\sigma})$ is quasi-Galois. By 3.8 and 7.7, modulo a ![]() ${\it\sigma}$-localization, we may assume that
${\it\sigma}$-localization, we may assume that ![]() $f$ is
$f$ is ![]() ${\it\sigma}$-pro-étale and that
${\it\sigma}$-pro-étale and that ![]() $h$ strictly dominates
$h$ strictly dominates ![]() $f$, that is, that the morphism
$f$, that is, that the morphism ![]() $r$ is surjective. Then
$r$ is surjective. Then
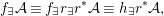 $$\begin{eqnarray}f_{\exists }{\mathcal{A}}\equiv f_{\exists }r_{\exists }r^{\ast }{\mathcal{A}}\equiv h_{\exists }r^{\ast }{\mathcal{A}},\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }{\mathcal{A}}\equiv f_{\exists }r_{\exists }r^{\ast }{\mathcal{A}}\equiv h_{\exists }r^{\ast }{\mathcal{A}},\end{eqnarray}$$ so it is enough to show that the direct image by ![]() $h_{\exists }$ of a Galois formula
$h_{\exists }$ of a Galois formula 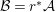 ${\mathcal{B}}=r^{\ast }{\mathcal{A}}$ is again Galois. In the effective case, we can do this via (†5), (†6), (†7).
${\mathcal{B}}=r^{\ast }{\mathcal{A}}$ is again Galois. In the effective case, we can do this via (†5), (†6), (†7).
For each ![]() ${\it\sigma}\in \mathring{\Sigma}$, let
${\it\sigma}\in \mathring{\Sigma}$, let ![]() ${\it\iota}_{{\it\sigma}}$ be the inclusion
${\it\iota}_{{\it\sigma}}$ be the inclusion  $\{{\it\sigma}\}{\hookrightarrow}\mathring{\Sigma}$, let
$\{{\it\sigma}\}{\hookrightarrow}\mathring{\Sigma}$, let 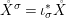 $\mathring{X}^{{\it\sigma}}={\it\iota}_{{\it\sigma}}^{\ast }\mathring{X}$ and let
$\mathring{X}^{{\it\sigma}}={\it\iota}_{{\it\sigma}}^{\ast }\mathring{X}$ and let 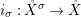 $i_{{\it\sigma}}:\mathring{X}^{{\it\sigma}}\rightarrow \mathring{X}$ be the natural morphism. Writing
$i_{{\it\sigma}}:\mathring{X}^{{\it\sigma}}\rightarrow \mathring{X}$ be the natural morphism. Writing 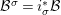 ${\mathcal{B}}^{{\it\sigma}}=i_{{\it\sigma}}^{\ast }{\mathcal{B}}$ and
${\mathcal{B}}^{{\it\sigma}}=i_{{\it\sigma}}^{\ast }{\mathcal{B}}$ and 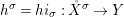 $h^{{\it\sigma}}=hi_{{\it\sigma}}:\mathring{X}^{{\it\sigma}}\rightarrow Y$, it is easily verified that
$h^{{\it\sigma}}=hi_{{\it\sigma}}:\mathring{X}^{{\it\sigma}}\rightarrow Y$, it is easily verified that
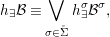 $$\begin{eqnarray}h_{\exists }{\mathcal{B}}\equiv \mathop{\vee }_{{\it\sigma}\in \mathring{\Sigma}}h_{\exists }^{{\it\sigma}}{\mathcal{B}}^{{\it\sigma}},\end{eqnarray}$$
$$\begin{eqnarray}h_{\exists }{\mathcal{B}}\equiv \mathop{\vee }_{{\it\sigma}\in \mathring{\Sigma}}h_{\exists }^{{\it\sigma}}{\mathcal{B}}^{{\it\sigma}},\end{eqnarray}$$so we can reduce the consideration to morphisms of ordinary difference schemes.
In other words, we may assume that the original 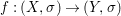 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is ![]() ${\it\sigma}$-pro-étale quasi-Galois
${\it\sigma}$-pro-étale quasi-Galois ![]() ${\it\sigma}$-separable, so we can benefit from Babbitt’s decomposition. Indeed, modulo a localization, 5.12 yields a decomposition of
${\it\sigma}$-separable, so we can benefit from Babbitt’s decomposition. Indeed, modulo a localization, 5.12 yields a decomposition of ![]() $f$ as
$f$ as
 $$\begin{eqnarray}(X,{\it\sigma})\simeq (X_{n},{\it\sigma})\rightarrow \cdots \rightarrow (X_{1},{\it\sigma})\rightarrow (X_{0},{\it\sigma})\rightarrow (Y,{\it\sigma}),\end{eqnarray}$$
$$\begin{eqnarray}(X,{\it\sigma})\simeq (X_{n},{\it\sigma})\rightarrow \cdots \rightarrow (X_{1},{\it\sigma})\rightarrow (X_{0},{\it\sigma})\rightarrow (Y,{\it\sigma}),\end{eqnarray}$$ with  $(X_{0},{\it\sigma})\rightarrow (Y,{\it\sigma})$ finite étale quasi-Galois, and for
$(X_{0},{\it\sigma})\rightarrow (Y,{\it\sigma})$ finite étale quasi-Galois, and for ![]() $i\geqslant 0$,
$i\geqslant 0$, 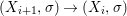 $(X_{i+1},{\it\sigma})\rightarrow (X_{i},{\it\sigma})$ étale benign quasi-Galois. This can be achieved in a
$(X_{i+1},{\it\sigma})\rightarrow (X_{i},{\it\sigma})$ étale benign quasi-Galois. This can be achieved in a ![]() $\dagger$-primitive recursive way by using (†4) and (†5).
$\dagger$-primitive recursive way by using (†4) and (†5).
We can therefore reduce to two subcases as follows.
Case 2(a). The morphism 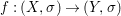 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is finite étale. We are given a Galois cover
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is finite étale. We are given a Galois cover 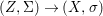 $(Z,{\rm\Sigma})\rightarrow (X,{\it\sigma})$ and a
$(Z,{\rm\Sigma})\rightarrow (X,{\it\sigma})$ and a 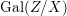 $\text{Gal}(Z/X)$-conjugacy class
$\text{Gal}(Z/X)$-conjugacy class ![]() $C$ in
$C$ in ![]() ${\rm\Sigma}$.
${\rm\Sigma}$.
The Galois closure (5.18) of a finite étale morphism consists of Galois covers 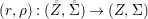 $(r,{\it\rho}):(\mathring{Z},\mathring{\Sigma})\rightarrow (Z,{\rm\Sigma})$ and
$(r,{\it\rho}):(\mathring{Z},\mathring{\Sigma})\rightarrow (Z,{\rm\Sigma})$ and 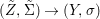 $(\tilde{Z},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$, as well as a morphism
$(\tilde{Z},\tilde{{\rm\Sigma}})\rightarrow (Y,{\it\sigma})$, as well as a morphism 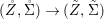 $(\mathring{Z},\mathring{\Sigma})\rightarrow (\tilde{Z},\tilde{{\rm\Sigma}})$ arising by restriction of structure via
$(\mathring{Z},\mathring{\Sigma})\rightarrow (\tilde{Z},\tilde{{\rm\Sigma}})$ arising by restriction of structure via 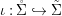 ${\it\iota}:\mathring{\Sigma}{\hookrightarrow}\tilde{{\rm\Sigma}}$.
${\it\iota}:\mathring{\Sigma}{\hookrightarrow}\tilde{{\rm\Sigma}}$.
Thus, using inflation and 7.11,
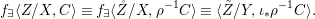 $$\begin{eqnarray}f_{\exists }\langle Z/X,C\rangle \equiv f_{\exists }\langle \mathring{Z}/X,{\it\rho}^{-1}C\rangle \equiv \langle \tilde{Z}/Y,{\it\iota}_{\ast }{\it\rho}^{-1}C\rangle .\end{eqnarray}$$
$$\begin{eqnarray}f_{\exists }\langle Z/X,C\rangle \equiv f_{\exists }\langle \mathring{Z}/X,{\it\rho}^{-1}C\rangle \equiv \langle \tilde{Z}/Y,{\it\iota}_{\ast }{\it\rho}^{-1}C\rangle .\end{eqnarray}$$The relevant calculations in the effective case are performed using (†7) and (†8).
Case 2(b). The morphism 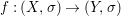 $f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is proper benign étale quasi-Galois. We are given a Galois cover
$f:(X,{\it\sigma})\rightarrow (Y,{\it\sigma})$ is proper benign étale quasi-Galois. We are given a Galois cover  $(Z,{\rm\Sigma}_{Z})\rightarrow (X,{\it\sigma})$ and a conjugacy domain
$(Z,{\rm\Sigma}_{Z})\rightarrow (X,{\it\sigma})$ and a conjugacy domain ![]() $C$ in
$C$ in ![]() ${\rm\Sigma}_{Z}$. The weak generic Galois closure (5.24) of
${\rm\Sigma}_{Z}$. The weak generic Galois closure (5.24) of ![]() $Z$ over
$Z$ over ![]() $Y$ consists of weak generic covers
$Y$ consists of weak generic covers ![]() $\mathring{Z}\rightarrow Z$ and
$\mathring{Z}\rightarrow Z$ and ![]() $\tilde{Z}\rightarrow Y$. Since
$\tilde{Z}\rightarrow Y$. Since ![]() $Z$ is a finite Galois cover of
$Z$ is a finite Galois cover of ![]() $X$ and
$X$ and ![]() $X$ is quasi-Galois over
$X$ is quasi-Galois over ![]() $Y$, it follows that
$Y$, it follows that ![]() $\mathring{Z}$ is a finite Galois cover of
$\mathring{Z}$ is a finite Galois cover of ![]() $X$. Thus, using inflation we can replace
$X$. Thus, using inflation we can replace ![]() $Z$ by
$Z$ by ![]() $\mathring{Z}$ and assume that the original
$\mathring{Z}$ and assume that the original ![]() $Z$ is in fact quasi-Galois over
$Z$ is in fact quasi-Galois over ![]() $Y$.
$Y$.
Babbitt’s decomposition 5.12 applied to ![]() $Z/Y$ yields a sequence
$Z/Y$ yields a sequence
 $$\begin{eqnarray}(Z,{\rm\Sigma}_{Z})\simeq (Z_{n},{\rm\Sigma}_{n})\rightarrow \cdots \rightarrow (Z_{1},{\rm\Sigma}_{1})\rightarrow (Z_{0},{\rm\Sigma}_{0})=(W,{\rm\Sigma}_{W})\rightarrow (Y,{\it\sigma})\end{eqnarray}$$
$$\begin{eqnarray}(Z,{\rm\Sigma}_{Z})\simeq (Z_{n},{\rm\Sigma}_{n})\rightarrow \cdots \rightarrow (Z_{1},{\rm\Sigma}_{1})\rightarrow (Z_{0},{\rm\Sigma}_{0})=(W,{\rm\Sigma}_{W})\rightarrow (Y,{\it\sigma})\end{eqnarray}$$ where 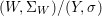 $(W,{\rm\Sigma}_{W})/(Y,{\it\sigma})$ can be assumed to be a finite étale Galois cover and
$(W,{\rm\Sigma}_{W})/(Y,{\it\sigma})$ can be assumed to be a finite étale Galois cover and 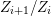 $Z_{i+1}/Z_{i}$ is benign for
$Z_{i+1}/Z_{i}$ is benign for ![]() $i\geqslant 0$. Since
$i\geqslant 0$. Since ![]() $\mathbf{k}(X)$ is linearly disjoint from
$\mathbf{k}(X)$ is linearly disjoint from ![]() $\mathbf{k}(W)$ over
$\mathbf{k}(W)$ over ![]() $\mathbf{k}(Y)$, we obtain an exact sequence of the form (3) again, and we have the corresponding
$\mathbf{k}(Y)$, we obtain an exact sequence of the form (3) again, and we have the corresponding ![]() $\mathit{Diff}$-morphism
$\mathit{Diff}$-morphism 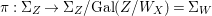 ${\it\pi}:{\rm\Sigma}_{Z}\rightarrow {\rm\Sigma}_{Z}/\text{Gal}(Z/W_{X})={\rm\Sigma}_{W}$. Let
${\it\pi}:{\rm\Sigma}_{Z}\rightarrow {\rm\Sigma}_{Z}/\text{Gal}(Z/W_{X})={\rm\Sigma}_{W}$. Let 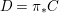 $D={\it\pi}_{\ast }C$ be the image of
$D={\it\pi}_{\ast }C$ be the image of ![]() $C$ in
$C$ in ![]() ${\rm\Sigma}_{W}$, and we claim that (4) holds for any
${\rm\Sigma}_{W}$, and we claim that (4) holds for any ![]() $s$ closed in
$s$ closed in ![]() $S$ and
$S$ and ![]() $(\bar{k},{\it\varphi}_{k})$ extending
$(\bar{k},{\it\varphi}_{k})$ extending 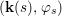 $(\mathbf{k}(s),{\it\varphi}_{s})$. To see the nontrivial inclusion, let
$(\mathbf{k}(s),{\it\varphi}_{s})$. To see the nontrivial inclusion, let ![]() $y$ be an element of the right-hand side and let
$y$ be an element of the right-hand side and let 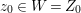 $z_{0}\in W=Z_{0}$ such that
$z_{0}\in W=Z_{0}$ such that ![]() $z_{0}\mapsto y$ and
$z_{0}\mapsto y$ and 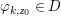 ${\it\varphi}_{k,z_{0}}\in D$. Using the property 5.9 repeatedly, we can lift
${\it\varphi}_{k,z_{0}}\in D$. Using the property 5.9 repeatedly, we can lift ![]() $z_{0}$ through the “stack” of benign extensions
$z_{0}$ through the “stack” of benign extensions 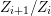 $Z_{i+1}/Z_{i}$ to a point
$Z_{i+1}/Z_{i}$ to a point 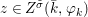 $z\in Z^{\tilde{{\it\sigma}}}(\bar{k},{\it\varphi}_{k})$ with
$z\in Z^{\tilde{{\it\sigma}}}(\bar{k},{\it\varphi}_{k})$ with ![]() $\tilde{{\it\sigma}}\in C$, and then the image
$\tilde{{\it\sigma}}\in C$, and then the image ![]() $x$ of
$x$ of ![]() $z$ in
$z$ in ![]() $X_{s}$ has the properties
$X_{s}$ has the properties 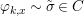 ${\it\varphi}_{k,x}\sim \tilde{{\it\sigma}}\in C$ and
${\it\varphi}_{k,x}\sim \tilde{{\it\sigma}}\in C$ and 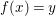 $f(x)=y$. This case is
$f(x)=y$. This case is ![]() $\dagger$-primitive recursive by (†2), (†5), (†6), (†8). ◻
$\dagger$-primitive recursive by (†2), (†5), (†6), (†8). ◻
Corollary 7.13. With assumptions of 7.12, it makes sense to define a subassignment
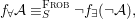 $$\begin{eqnarray}f_{\forall }{\mathcal{A}}\equiv _{S}^{{\rm \small{Frob}}}\neg f_{\exists }(\neg {\mathcal{A}}),\end{eqnarray}$$
$$\begin{eqnarray}f_{\forall }{\mathcal{A}}\equiv _{S}^{{\rm \small{Frob}}}\neg f_{\exists }(\neg {\mathcal{A}}),\end{eqnarray}$$ and it is again a Galois formula on ![]() $Y$.
$Y$.
7.3 Quantifier elimination for Galois formulas
Let ![]() $(R,{\it\sigma})$ be an integral normal difference ring of finite
$(R,{\it\sigma})$ be an integral normal difference ring of finite ![]() ${\it\sigma}$-type over
${\it\sigma}$-type over ![]() $\mathbb{Z}$, and let
$\mathbb{Z}$, and let 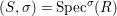 $(S,{\it\sigma})=\text{Spec}^{{\it\sigma}}(R)$.
$(S,{\it\sigma})=\text{Spec}^{{\it\sigma}}(R)$.
(1) A first-order formula over
 $(S,{\it\sigma})$ is a first-order expression built in the usual way starting from terms which are difference polynomials with coefficients in
$(S,{\it\sigma})$ is a first-order expression built in the usual way starting from terms which are difference polynomials with coefficients in  $(R,{\it\sigma})$. If
$(R,{\it\sigma})$. If  $x_{1},\ldots ,x_{n}$ are the free variables of a formula
$x_{1},\ldots ,x_{n}$ are the free variables of a formula  ${\it\theta}$, and
${\it\theta}$, and  $r_{1},\ldots ,r_{m}\in R$ are all the coefficients of all polynomials appearing as terms of
$r_{1},\ldots ,r_{m}\in R$ are all the coefficients of all polynomials appearing as terms of  ${\it\theta}$, we can express this dependence by writing where the
${\it\theta}$, we can express this dependence by writing where the $$\begin{eqnarray}{\it\theta}(x_{1},\ldots ,x_{n};r_{1},\ldots ,r_{n}),\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}(x_{1},\ldots ,x_{n};r_{1},\ldots ,r_{n}),\end{eqnarray}$$ $r_{i}$ are thought of as parameters of
$r_{i}$ are thought of as parameters of  ${\it\theta}$.
${\it\theta}$.(2) An
 $(R,{\it\sigma})$-formula
$(R,{\it\sigma})$-formula  ${\it\theta}(x_{1},\ldots ,x_{n};r_{1},\ldots ,r_{n})$ gives rise to a subassignment
${\it\theta}(x_{1},\ldots ,x_{n};r_{1},\ldots ,r_{n})$ gives rise to a subassignment  $\tilde{{\it\theta}}$ of
$\tilde{{\it\theta}}$ of  $\mathbb{A}_{(S,{\it\sigma})}^{n}$ by the following procedure. Let
$\mathbb{A}_{(S,{\it\sigma})}^{n}$ by the following procedure. Let  $s\in S$, and let
$s\in S$, and let  $(F,{\it\varphi})$ be an algebraically closed difference field extending
$(F,{\it\varphi})$ be an algebraically closed difference field extending  $(\mathbf{k}(s),{\it\varphi}^{s})$. Taking the images of the
$(\mathbf{k}(s),{\it\varphi}^{s})$. Taking the images of the  $r_{i}$ by the composite we obtain an honest first-order formula in the language of difference rings on the field
$r_{i}$ by the composite we obtain an honest first-order formula in the language of difference rings on the field $$\begin{eqnarray}(R,{\it\sigma})\rightarrow ({\mathcal{O}}_{S,s},{\it\sigma}_{s}^{\sharp })\rightarrow (\mathbf{k}(s),{\it\sigma}^{s})\rightarrow (F,{\it\varphi}),\end{eqnarray}$$
$$\begin{eqnarray}(R,{\it\sigma})\rightarrow ({\mathcal{O}}_{S,s},{\it\sigma}_{s}^{\sharp })\rightarrow (\mathbf{k}(s),{\it\sigma}^{s})\rightarrow (F,{\it\varphi}),\end{eqnarray}$$ $(F,{\it\varphi})$, and we take its set of realizations to be the value
$(F,{\it\varphi})$, and we take its set of realizations to be the value  $$\begin{eqnarray}\tilde{{\it\theta}}(s,(F,{\it\varphi}))\subseteq \mathbb{A}_{s}^{n}(F,{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\it\theta}}(s,(F,{\it\varphi}))\subseteq \mathbb{A}_{s}^{n}(F,{\it\varphi}).\end{eqnarray}$$(3) An
 $(S,{\it\sigma})$-subassignment
$(S,{\it\sigma})$-subassignment  ${\mathcal{F}}$ of
${\mathcal{F}}$ of  $\mathbb{A}_{S}^{n}$ is called definable if there exists a first-order formula
$\mathbb{A}_{S}^{n}$ is called definable if there exists a first-order formula  ${\it\theta}(x_{1},\ldots ,x_{n})$ over
${\it\theta}(x_{1},\ldots ,x_{n})$ over  $(R,{\it\sigma})$ such that
$(R,{\it\sigma})$ such that  ${\mathcal{F}}=\tilde{{\it\theta}}$.
${\mathcal{F}}=\tilde{{\it\theta}}$.
Theorem 7.15. (Quantifier elimination for fields with Frobenii)
The class of definable ![]() $(S,{\it\sigma})$-subassignments is equal to the class of
$(S,{\it\sigma})$-subassignments is equal to the class of ![]() $(S,{\it\sigma})$-Galois formulas modulo the relation
$(S,{\it\sigma})$-Galois formulas modulo the relation ![]() $\equiv _{S}^{{\rm \small{Frob}}}$, that is, with respect to fields with Frobenii over
$\equiv _{S}^{{\rm \small{Frob}}}$, that is, with respect to fields with Frobenii over ![]() $S$. The quantifier elimination procedure is
$S$. The quantifier elimination procedure is ![]() $\dagger$-primitive recursive.
$\dagger$-primitive recursive.
Proof. Let us show by induction on the complexity of a first-order formula that every ![]() $(S,{\it\sigma})$-formula in the language of rings
$(S,{\it\sigma})$-formula in the language of rings 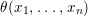 ${\it\theta}(x_{1},\ldots ,x_{n})$ is equivalent to a Galois formula on
${\it\theta}(x_{1},\ldots ,x_{n})$ is equivalent to a Galois formula on ![]() $\mathbb{A}_{(S,{\it\sigma})}^{n}$.
$\mathbb{A}_{(S,{\it\sigma})}^{n}$.
(1) If
 ${\it\theta}(x_{1},\ldots ,x_{n})$ is a positive atomic formula, it is given by a difference-polynomial equation
${\it\theta}(x_{1},\ldots ,x_{n})$ is a positive atomic formula, it is given by a difference-polynomial equation  $P(x_{1},\ldots ,x_{n})=0$, which cuts out a closed difference subscheme
$P(x_{1},\ldots ,x_{n})=0$, which cuts out a closed difference subscheme  $Z$ of
$Z$ of  $\mathbb{A}_{(S,{\it\sigma})}^{n}$. We can stratify the affine space into normal locally closed pieces
$\mathbb{A}_{(S,{\it\sigma})}^{n}$. We can stratify the affine space into normal locally closed pieces  $X_{i}$ such that each piece is either completely in
$X_{i}$ such that each piece is either completely in  $Z$ or in its complement. For each
$Z$ or in its complement. For each  $X_{i}$, we choose a trivial Galois cover
$X_{i}$, we choose a trivial Galois cover  $(X_{i},{\it\sigma})\rightarrow (X_{i},{\it\sigma})$, and we let
$(X_{i},{\it\sigma})\rightarrow (X_{i},{\it\sigma})$, and we let  $C_{i}=\{{\it\sigma}\}$ when
$C_{i}=\{{\it\sigma}\}$ when  $X_{i}\subseteq Z$, and
$X_{i}\subseteq Z$, and  $C_{i}=\emptyset$ otherwise. Then
$C_{i}=\emptyset$ otherwise. Then  ${\mathcal{A}}=\langle \mathbb{A}_{S}^{n},X_{i}/X_{i},C_{i}\rangle$ has the property that
${\mathcal{A}}=\langle \mathbb{A}_{S}^{n},X_{i}/X_{i},C_{i}\rangle$ has the property that  $$\begin{eqnarray}\tilde{{\it\theta}}\equiv \tilde{{\mathcal{A}}}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\it\theta}}\equiv \tilde{{\mathcal{A}}}.\end{eqnarray}$$(2) If
 ${\it\theta}(\bar{x})={\it\theta}_{1}(\bar{x}_{1})\wedge {\it\theta}_{2}(\bar{x}_{2})$, where it is assumed that
${\it\theta}(\bar{x})={\it\theta}_{1}(\bar{x}_{1})\wedge {\it\theta}_{2}(\bar{x}_{2})$, where it is assumed that  $\bar{x}$ is the union of variables in
$\bar{x}$ is the union of variables in  $\bar{x}_{1}$ and
$\bar{x}_{1}$ and  $\bar{x}_{2}$, we choose the corresponding projections
$\bar{x}_{2}$, we choose the corresponding projections  $p_{i}:\mathbb{A}^{|\bar{x}|}\rightarrow \mathbb{A}^{|\bar{x}_{i}|}$. By induction hypothesis, we can find Galois formulas
$p_{i}:\mathbb{A}^{|\bar{x}|}\rightarrow \mathbb{A}^{|\bar{x}_{i}|}$. By induction hypothesis, we can find Galois formulas  ${\mathcal{A}}_{i}$ on
${\mathcal{A}}_{i}$ on  $\mathbb{A}^{|\bar{x}_{i}|}$ such that
$\mathbb{A}^{|\bar{x}_{i}|}$ such that  ${\it\theta}_{i}\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}_{i}$. Then
${\it\theta}_{i}\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}_{i}$. Then  $$\begin{eqnarray}{\it\theta}\equiv _{S}^{{\rm \small{Frob}}}p_{1}^{\ast }{\mathcal{A}}_{1}\wedge p_{2}^{\ast }{\mathcal{A}}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}\equiv _{S}^{{\rm \small{Frob}}}p_{1}^{\ast }{\mathcal{A}}_{1}\wedge p_{2}^{\ast }{\mathcal{A}}_{2}.\end{eqnarray}$$(3) If
 ${\it\theta}={\it\theta}_{1}\vee {\it\theta}_{2}$, we proceed analogously to the previous step.
${\it\theta}={\it\theta}_{1}\vee {\it\theta}_{2}$, we proceed analogously to the previous step.(4) If
 ${\it\theta}=\neg {\it\theta}^{\prime }$, and
${\it\theta}=\neg {\it\theta}^{\prime }$, and  ${\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}$, then
${\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}$, then  $$\begin{eqnarray}{\it\theta}\equiv _{S}^{{\rm \small{Frob}}}\neg {\mathcal{A}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}\equiv _{S}^{{\rm \small{Frob}}}\neg {\mathcal{A}}.\end{eqnarray}$$(5) If
 ${\it\theta}(x_{2},\ldots ,x_{n})=\exists x_{1}{\it\theta}^{\prime }(x_{1},x_{2},\ldots ,x_{n})$, and
${\it\theta}(x_{2},\ldots ,x_{n})=\exists x_{1}{\it\theta}^{\prime }(x_{1},x_{2},\ldots ,x_{n})$, and  ${\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}$ on
${\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}$ on  $\mathbb{A}^{n}$, writing
$\mathbb{A}^{n}$, writing  $x_{1}$ for the projection
$x_{1}$ for the projection  $\mathbb{A}^{n}\rightarrow \mathbb{A}^{n-1}$ to the variables
$\mathbb{A}^{n}\rightarrow \mathbb{A}^{n-1}$ to the variables  $x_{2},\ldots ,x_{n}$, we have that which is Galois by 7.12.
$x_{2},\ldots ,x_{n}$, we have that which is Galois by 7.12. $$\begin{eqnarray}{\it\theta}\equiv _{S}\exists x_{1}{\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{x_{1}}_{\exists }{\mathcal{A}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}\equiv _{S}\exists x_{1}{\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{x_{1}}_{\exists }{\mathcal{A}},\end{eqnarray}$$(6) If
 ${\it\theta}=\forall x_{1}{\it\theta}^{\prime }$, and
${\it\theta}=\forall x_{1}{\it\theta}^{\prime }$, and  ${\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}$, then which is Galois by 7.13.
${\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{\mathcal{A}}$, then which is Galois by 7.13. $$\begin{eqnarray}{\it\theta}\equiv _{S}\forall x_{1}{\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{x_{1}}_{\forall }{\mathcal{A}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\theta}\equiv _{S}\forall x_{1}{\it\theta}^{\prime }\equiv _{S}^{{\rm \small{Frob}}}{x_{1}}_{\forall }{\mathcal{A}},\end{eqnarray}$$
We have checked all cases so the induction is complete. Note that working over fields with Frobenii is only crucial in steps (5) and (6).
Conversely, suppose we have a Galois stratification 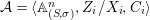 ${\mathcal{A}}=\langle \mathbb{A}_{(S,{\it\sigma})}^{n},Z_{i}/X_{i},C_{i}\rangle$. By refining it further, we may assume that each Galois cover
${\mathcal{A}}=\langle \mathbb{A}_{(S,{\it\sigma})}^{n},Z_{i}/X_{i},C_{i}\rangle$. By refining it further, we may assume that each Galois cover 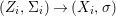 $(Z_{i},{\rm\Sigma}_{i})\rightarrow (X_{i},{\it\sigma})$ with group
$(Z_{i},{\rm\Sigma}_{i})\rightarrow (X_{i},{\it\sigma})$ with group ![]() $(G,\tilde{{\rm\Sigma}})$ is embedded in some affine space, in the sense that
$(G,\tilde{{\rm\Sigma}})$ is embedded in some affine space, in the sense that ![]() $Z_{i}$ is embedded in some
$Z_{i}$ is embedded in some ![]() $\mathbb{A}_{S}^{m}$, and all automorphisms corresponding to elements of
$\mathbb{A}_{S}^{m}$, and all automorphisms corresponding to elements of ![]() $G$ are restrictions of difference rational endomorphisms of
$G$ are restrictions of difference rational endomorphisms of ![]() $\mathbb{A}_{S}^{m}$ to
$\mathbb{A}_{S}^{m}$ to ![]() $Z_{i}$, and the canonical projection
$Z_{i}$, and the canonical projection 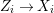 $Z_{i}\rightarrow X_{i}$ is a restriction of difference rational morphism
$Z_{i}\rightarrow X_{i}$ is a restriction of difference rational morphism 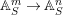 $\mathbb{A}_{S}^{m}\rightarrow \mathbb{A}_{S}^{n}$. Then, if
$\mathbb{A}_{S}^{m}\rightarrow \mathbb{A}_{S}^{n}$. Then, if ![]() $C_{i}$ is the conjugacy class of some element
$C_{i}$ is the conjugacy class of some element ![]() ${\it\sigma}_{i}\in {\rm\Sigma}$, the set
${\it\sigma}_{i}\in {\rm\Sigma}$, the set
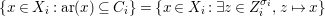 $$\begin{eqnarray}\{x\in X_{i}:\text{ar}(x)\subseteq C_{i}\}=\{x\in X_{i}:\exists z\in Z_{i}^{{\it\sigma}_{i}},z\mapsto x\}\end{eqnarray}$$
$$\begin{eqnarray}\{x\in X_{i}:\text{ar}(x)\subseteq C_{i}\}=\{x\in X_{i}:\exists z\in Z_{i}^{{\it\sigma}_{i}},z\mapsto x\}\end{eqnarray}$$ is clearly expressible (working over algebraically closed difference fields) in a first-order way using an existential formula in the language of difference rings. When ![]() $C_{i}$ is a union of conjugacy classes, we take the disjunction of the corresponding difference ring formulas.◻
$C_{i}$ is a union of conjugacy classes, we take the disjunction of the corresponding difference ring formulas.◻
Let ![]() $T_{\infty }$ be the set of first-order sentences true in difference fields
$T_{\infty }$ be the set of first-order sentences true in difference fields ![]() $(\bar{k},{\it\varphi}_{k})$ with
$(\bar{k},{\it\varphi}_{k})$ with ![]() $k$ a sufficiently large finite field.
$k$ a sufficiently large finite field.
Corollary 7.16. The theory ![]() $T_{\infty }$ is decidable by a
$T_{\infty }$ is decidable by a ![]() $\dagger$-primitive recursive procedure. Moreover, for each first-order sentence
$\dagger$-primitive recursive procedure. Moreover, for each first-order sentence ![]() ${\it\theta}\in T_{\infty }$ a
${\it\theta}\in T_{\infty }$ a ![]() $\dagger$-primitive recursive procedure can compute the (finite) list of exceptional finite fields
$\dagger$-primitive recursive procedure can compute the (finite) list of exceptional finite fields ![]() $k$ such that
$k$ such that ![]() ${\it\theta}$ does not hold in
${\it\theta}$ does not hold in ![]() $(\bar{k},{\it\varphi}_{k})$.
$(\bar{k},{\it\varphi}_{k})$.
Proof. The quantifier elimination procedure produces a Galois stratification ![]() ${\mathcal{A}}$ on the base
${\mathcal{A}}$ on the base  $S=\text{Spec}(\mathbb{Z})$ and a constant
$S=\text{Spec}(\mathbb{Z})$ and a constant ![]() $m$ such that for every
$m$ such that for every ![]() $p\in S$, and every
$p\in S$, and every ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$ with
$p$ with ![]() $|k|\geqslant m$,
$|k|\geqslant m$, 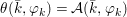 ${\it\theta}(\bar{k},{\it\varphi}_{k})={\mathcal{A}}(\bar{k},{\it\varphi}_{k})$. The stratification
${\it\theta}(\bar{k},{\it\varphi}_{k})={\mathcal{A}}(\bar{k},{\it\varphi}_{k})$. The stratification ![]() ${\mathcal{A}}$ stipulates the existence of a localization
${\mathcal{A}}$ stipulates the existence of a localization 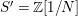 $S^{\prime }=\mathbb{Z}[1/N]$ of
$S^{\prime }=\mathbb{Z}[1/N]$ of ![]() $S$, a Galois cover
$S$, a Galois cover ![]() $Z/S^{\prime }$ and a conjugacy class
$Z/S^{\prime }$ and a conjugacy class ![]() $C$ in
$C$ in 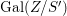 $\text{Gal}(Z/S^{\prime })$ such that, for
$\text{Gal}(Z/S^{\prime })$ such that, for ![]() $p\in S^{\prime }$ (i.e., for
$p\in S^{\prime }$ (i.e., for ![]() $p$ not dividing
$p$ not dividing ![]() $N$), and
$N$), and ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$ with
$p$ with ![]() $|k|\geqslant m$,
$|k|\geqslant m$, ![]() ${\it\theta}$ holds in
${\it\theta}$ holds in ![]() $(\bar{k},{\it\varphi}_{k})$ if and only if
$(\bar{k},{\it\varphi}_{k})$ if and only if ![]() ${\it\varphi}_{k}\in C$. By (the classical) Chebotarev’s density theorem, this can hold for all but finitely many
${\it\varphi}_{k}\in C$. By (the classical) Chebotarev’s density theorem, this can hold for all but finitely many ![]() $p$ if and only if
$p$ if and only if 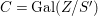 $C=\text{Gal}(Z/S^{\prime })$, which can be effectively checked by (†8).
$C=\text{Gal}(Z/S^{\prime })$, which can be effectively checked by (†8).
For each field ![]() $(\bar{k},{\it\varphi}_{k})$ with characteristic of
$(\bar{k},{\it\varphi}_{k})$ with characteristic of ![]() $k$ dividing
$k$ dividing ![]() $N$, or
$N$, or ![]() $|k|<m$, once we interpret
$|k|<m$, once we interpret ![]() ${\it\sigma}$ as the Frobenius
${\it\sigma}$ as the Frobenius ![]() ${\it\varphi}_{k}$ with
${\it\varphi}_{k}$ with 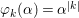 ${\it\varphi}_{k}({\it\alpha})={\it\alpha}^{|k|}$, the formula
${\it\varphi}_{k}({\it\alpha})={\it\alpha}^{|k|}$, the formula ![]() ${\it\theta}$ can be treated as a formula in the language of rings, which can be decided by the well-known primitive recursive decision procedure for the algebraically closed field
${\it\theta}$ can be treated as a formula in the language of rings, which can be decided by the well-known primitive recursive decision procedure for the algebraically closed field ![]() $\bar{k}$.◻
$\bar{k}$.◻
A model-theoretic restatement of the above theorem would say that the theory ![]() $T_{\infty }$ of fields with Frobenii allows quantifier elimination down to the class of Galois formulas. Given that
$T_{\infty }$ of fields with Frobenii allows quantifier elimination down to the class of Galois formulas. Given that ![]() $T_{\infty }$ happens to be [Reference Hrushovski18] the theory of existentially closed difference fields (ACFA), let us state an appropriate analog of the above result.
$T_{\infty }$ happens to be [Reference Hrushovski18] the theory of existentially closed difference fields (ACFA), let us state an appropriate analog of the above result.
We must emphasize that the statement below can be obtained unconditionally, that is, without appealing to [Reference Hrushovski18], by replacing the use of [Reference Tomašić24, 4.2] in the present paper by the use of existential closedness of models of ACFA (i.e., by the use of the “ACFA-axiom”). This will be done in a separate paper [Reference Tomašić25].
Theorem 7.17. Let ![]() $(k,{\it\sigma})$ be a difference field. Let
$(k,{\it\sigma})$ be a difference field. Let 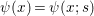 ${\it\psi}(x)={\it\psi}(x;s)$ be a first-order formula in the language of difference rings in variables
${\it\psi}(x)={\it\psi}(x;s)$ be a first-order formula in the language of difference rings in variables 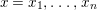 $x=x_{1},\ldots ,x_{n}$ with parameters
$x=x_{1},\ldots ,x_{n}$ with parameters ![]() $s$ from
$s$ from ![]() $k$. There exists a Galois stratification
$k$. There exists a Galois stratification ![]() ${\mathcal{A}}$ of the difference affine
${\mathcal{A}}$ of the difference affine ![]() $n$-space over
$n$-space over ![]() $k$ such that for every model
$k$ such that for every model ![]() $(F,{\it\varphi})$ of ACFA which extends
$(F,{\it\varphi})$ of ACFA which extends ![]() $(k,{\it\sigma})$,
$(k,{\it\sigma})$,
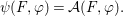 $$\begin{eqnarray}{\it\psi}(F,{\it\varphi})={\mathcal{A}}(F,{\it\varphi}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\psi}(F,{\it\varphi})={\mathcal{A}}(F,{\it\varphi}).\end{eqnarray}$$Acknowledgments
The author would like to thank Michael Fried, Angus Macintyre, Thomas Scanlon and Michael Wibmer for fruitful discussions on the topic of this paper, and Zoe Chatzidakis for pointing out the importance of Babbitt’s decomposition and for helping to improve a preliminary version of the paper. We gratefully acknowledge the hospitality of IHES Paris and MPIM Bonn, where significant parts of the paper were produced.