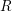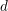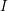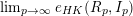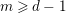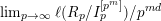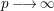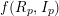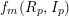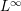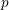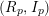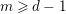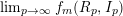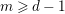1 Introduction
Let
![]() $R$
be a Noetherian ring of prime characteristic
$R$
be a Noetherian ring of prime characteristic
![]() $p>0$
and of dimension
$p>0$
and of dimension
![]() $d$
, and let
$d$
, and let
![]() $I\subseteq R$
be an ideal of finite colength. Then, we recall that the Hilbert–Kunz multiplicity of
$I\subseteq R$
be an ideal of finite colength. Then, we recall that the Hilbert–Kunz multiplicity of
![]() $R$
with respect to
$R$
with respect to
![]() $I$
is defined as
$I$
is defined as
where
![]() $I^{[p^{n}]}$
= the
$I^{[p^{n}]}$
= the
![]() $n$
th Frobenius power of
$n$
th Frobenius power of
![]() $I$
= the ideal generated by
$I$
= the ideal generated by
![]() $p^{n}$
th power of elements of
$p^{n}$
th power of elements of
![]() $I$
. This is an ideal of finite colength, and
$I$
. This is an ideal of finite colength, and
![]() $\ell (R/I^{[p^{n}]})$
denotes the length of the
$\ell (R/I^{[p^{n}]})$
denotes the length of the
![]() $R$
-module
$R$
-module
![]() $R/I^{[p^{n}]}$
. This invariant was introduced by E. Kunz and existence of the limit was proved by Monsky (see Theorem 1.8 in [Reference MonskyMo1]). It carries information about char
$R/I^{[p^{n}]}$
. This invariant was introduced by E. Kunz and existence of the limit was proved by Monsky (see Theorem 1.8 in [Reference MonskyMo1]). It carries information about char
![]() $p$
related properties of the ring, but at the same time is difficult to compute (even in the graded case), as various standard techniques, used for studying multiplicities, are not applicable for the invariant
$p$
related properties of the ring, but at the same time is difficult to compute (even in the graded case), as various standard techniques, used for studying multiplicities, are not applicable for the invariant
![]() $e_{HK}$
.
$e_{HK}$
.
It is natural to ask whether the notion of this invariant can be extended to the “char 0” case by studying the behavior of mod
![]() $p$
reductions.
$p$
reductions.
A natural way to attempt this, for a pair
![]() $(R,I)$
(from now onwards, unless stated otherwise, by a pair
$(R,I)$
(from now onwards, unless stated otherwise, by a pair
![]() $(R,I)$
, we mean that
$(R,I)$
, we mean that
![]() $R$
is a standard graded ring and
$R$
is a standard graded ring and
![]() $I\subset R$
is a graded ideal of finite colength), could be as follows. Suppose that
$I\subset R$
is a graded ideal of finite colength), could be as follows. Suppose that
![]() $R$
is a finitely generated algebra and a domain over a field
$R$
is a finitely generated algebra and a domain over a field
![]() $k$
of characteristic 0, and
$k$
of characteristic 0, and
![]() $I\subseteq R$
is an ideal of finite colength. Let
$I\subseteq R$
is an ideal of finite colength. Let
![]() $(A,R_{A},I_{A})$
be a spread of the pair
$(A,R_{A},I_{A})$
be a spread of the pair
![]() $(R,I)$
(see Definition 3.2), where
$(R,I)$
(see Definition 3.2), where
![]() $A\subset k$
is a finitely generated algebra over
$A\subset k$
is a finitely generated algebra over
![]() $\mathbb{Z}$
. Then, we may define
$\mathbb{Z}$
. Then, we may define
where
![]() $R_{s}=R_{A}\otimes _{A}\bar{k}(s)$
and
$R_{s}=R_{A}\otimes _{A}\bar{k}(s)$
and
![]() $I_{s}=I_{A}\otimes _{A}\bar{k}(s)$
, with
$I_{s}=I_{A}\otimes _{A}\bar{k}(s)$
, with
![]() $\bar{k}(s)$
as the algebraic closure of
$\bar{k}(s)$
as the algebraic closure of
![]() $k(s)$
with
$k(s)$
with
![]() $\text{char}~k(s)=p_{s}$
, and
$\text{char}~k(s)=p_{s}$
, and
![]() $s$
is a closed point of
$s$
is a closed point of
![]() $\text{Spec}(A)$
(the definition is tentative, since the existence of this limit is not known in general). Or consider a simpler situation:
$\text{Spec}(A)$
(the definition is tentative, since the existence of this limit is not known in general). Or consider a simpler situation:
![]() $R$
is a finitely generated
$R$
is a finitely generated
![]() $\mathbb{Z}$
-algebra and a domain,
$\mathbb{Z}$
-algebra and a domain,
![]() $I\subset R$
, such that
$I\subset R$
, such that
![]() $R/I$
is an abelian group of finite rank. Then, let
$R/I$
is an abelian group of finite rank. Then, let
In case of dimension
![]() $R=1$
, we know that the Hilbert–Kunz multiplicity coincides with the Hilbert–Samuel multiplicity; hence, it is independent of
$R=1$
, we know that the Hilbert–Kunz multiplicity coincides with the Hilbert–Samuel multiplicity; hence, it is independent of
![]() $p$
, for large
$p$
, for large
![]() $p$
.
$p$
.
For homogeneous coordinate rings of plane curves with respect to the maximal graded ideal (in [Reference TrivediT1], [Reference MonskyMo3]), nonsingular curves with respect to a graded ideal
![]() $I$
(in [Reference TrivediT2]), and diagonal hypersurfaces (in [Reference Gessel and MonskyGM] and [Reference Hans and MonskyHM]), it has been shown that
$I$
(in [Reference TrivediT2]), and diagonal hypersurfaces (in [Reference Gessel and MonskyGM] and [Reference Hans and MonskyHM]), it has been shown that
![]() $e_{HK}(R_{p},I_{p})$
varies with
$e_{HK}(R_{p},I_{p})$
varies with
![]() $p$
, and the limit exists as
$p$
, and the limit exists as
![]() $p\rightarrow \infty$
. Then, there are other cases where
$p\rightarrow \infty$
. Then, there are other cases where
![]() $e_{HK}(R_{p},I_{p})$
is independent of
$e_{HK}(R_{p},I_{p})$
is independent of
![]() $p$
: plane cubics (by [Reference Buchweitz and ChenBC], [Reference MonskyMo2] and [Reference PardueP]), certain monomial ideals (by [Reference BrunsBr], [Reference ConcaC], [Reference EtoE], [Reference WatanabeW]), two-dimensional invariant rings for finite group actions (by [Reference Watanabe and YoshidaWY2]), and full flag varieties and elliptic curves (by [Reference Fakhruddin and TrivediFT]). Therefore, the limit exists in all of these cases.
$p$
: plane cubics (by [Reference Buchweitz and ChenBC], [Reference MonskyMo2] and [Reference PardueP]), certain monomial ideals (by [Reference BrunsBr], [Reference ConcaC], [Reference EtoE], [Reference WatanabeW]), two-dimensional invariant rings for finite group actions (by [Reference Watanabe and YoshidaWY2]), and full flag varieties and elliptic curves (by [Reference Fakhruddin and TrivediFT]). Therefore, the limit exists in all of these cases.
Since
it seems harder to compute as such, as the inner limit
![]() $\lim _{n\rightarrow \infty }\ell (R_{p}/I_{p}^{[p^{n}]})/(p^{n})^{d}$
itself does not seem easily computable (even in the graded case). In the special situation considered by Gessel and Monsky (see [Reference Gessel and MonskyGM]), the existence of
$\lim _{n\rightarrow \infty }\ell (R_{p}/I_{p}^{[p^{n}]})/(p^{n})^{d}$
itself does not seem easily computable (even in the graded case). In the special situation considered by Gessel and Monsky (see [Reference Gessel and MonskyGM]), the existence of
![]() $e_{HK}^{\infty }$
is proved by reducing the problem to the existence of
$e_{HK}^{\infty }$
is proved by reducing the problem to the existence of
![]() $\lim _{p\rightarrow \infty }(\ell (R_{p}/I_{p}^{[p]})/p^{d})$
. To make this invariant more approachable in a general graded case, the following question was posed in [Reference Brenner, Li and MillerBLM] (see the introduction).
$\lim _{p\rightarrow \infty }(\ell (R_{p}/I_{p}^{[p]})/p^{d})$
. To make this invariant more approachable in a general graded case, the following question was posed in [Reference Brenner, Li and MillerBLM] (see the introduction).
Question. Supposing that
![]() $e_{HK}^{\infty }(R,I)$
exists, is it true that for any fixed
$e_{HK}^{\infty }(R,I)$
exists, is it true that for any fixed
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
The main result of their paper was to give an affirmative answer in the case of a two-dimensional standard graded normal domain
![]() $R$
with respect to a homogeneous ideal
$R$
with respect to a homogeneous ideal
![]() $I$
of finite colength. Note that the existence of
$I$
of finite colength. Note that the existence of
![]() $e_{HK}^{\infty }(R,I)$
, in this case, was proved earlier in [Reference TrivediT2].
$e_{HK}^{\infty }(R,I)$
, in this case, was proved earlier in [Reference TrivediT2].
Recall that for a vector bundle
![]() $V$
on a smooth (projective and polarized) variety, we have the well defined Harder–Narasimhan (HN) data, namely
$V$
on a smooth (projective and polarized) variety, we have the well defined Harder–Narasimhan (HN) data, namely
![]() $\{r_{i}(V),\unicode[STIX]{x1D707}_{i}(V)\}_{i}$
, where
$\{r_{i}(V),\unicode[STIX]{x1D707}_{i}(V)\}_{i}$
, where
![]() $r_{i}(V)=\text{rank}(E_{i}/E_{i-1})$
,
$r_{i}(V)=\text{rank}(E_{i}/E_{i-1})$
,
![]() $\unicode[STIX]{x1D707}_{i}(V)=\text{slope of}~E_{i}/E_{i-1}$
, and
$\unicode[STIX]{x1D707}_{i}(V)=\text{slope of}~E_{i}/E_{i-1}$
, and
is the HN filtration of
![]() $V$
.
$V$
.
Let
![]() $X_{p}=\text{Proj}~R_{p}$
, which is a nonsingular projective curve, and let
$X_{p}=\text{Proj}~R_{p}$
, which is a nonsingular projective curve, and let
![]() $I_{p}$
be generated by homogeneous elements of degrees
$I_{p}$
be generated by homogeneous elements of degrees
![]() $d_{1},\ldots ,d_{\unicode[STIX]{x1D707}}$
; then, we have the vector bundle
$d_{1},\ldots ,d_{\unicode[STIX]{x1D707}}$
; then, we have the vector bundle
![]() $V_{p}$
on
$V_{p}$
on
![]() $X_{p}$
given by the following canonical exact sequence of
$X_{p}$
given by the following canonical exact sequence of
![]() ${\mathcal{O}}_{X_{p}}$
-modules:
${\mathcal{O}}_{X_{p}}$
-modules:
Then, by [Reference TrivediT2, Proposition 1.16], there is a constant
![]() $C$
determined by genus of
$C$
determined by genus of
![]() $X_{p}$
and
$X_{p}$
and
![]() $\text{rank}~V_{p}$
(hence independent of
$\text{rank}~V_{p}$
(hence independent of
![]() $p$
), such that for
$p$
), such that for
![]() $s\geqslant 1$
,
$s\geqslant 1$
,
 $$\begin{eqnarray}\left|\mathop{\sum }_{j}r_{j}(F^{s\ast }V_{p})\unicode[STIX]{x1D707}_{j}(F^{s\ast }V_{p})^{2}-\mathop{\sum }_{i}r_{i}(V_{p})\unicode[STIX]{x1D707}_{i}(V_{p})^{2}\right|\leqslant C/p.\end{eqnarray}$$
$$\begin{eqnarray}\left|\mathop{\sum }_{j}r_{j}(F^{s\ast }V_{p})\unicode[STIX]{x1D707}_{j}(F^{s\ast }V_{p})^{2}-\mathop{\sum }_{i}r_{i}(V_{p})\unicode[STIX]{x1D707}_{i}(V_{p})^{2}\right|\leqslant C/p.\end{eqnarray}$$
(Here,
![]() $F$
is the absolute Frobenius morphism, and
$F$
is the absolute Frobenius morphism, and
![]() $F^{s}$
is the
$F^{s}$
is the
![]() $s$
-fold iterate.) Note that the HN filtration and hence the HN data of
$s$
-fold iterate.) Note that the HN filtration and hence the HN data of
![]() $V_{p}$
stabilize for
$V_{p}$
stabilize for
![]() $p\gg 0$
(see [Reference MaruyamaMar]).
$p\gg 0$
(see [Reference MaruyamaMar]).
Thus, here,
(1) one relates
 $\ell (R_{p}/I_{p}^{[p^{s}]})$
with the HN data of
$\ell (R_{p}/I_{p}^{[p^{s}]})$
with the HN data of
 $F^{s\ast }V_{p}$
, for
$F^{s\ast }V_{p}$
, for
 $s\geqslant 1$
(see [Reference BrennerB] and [Reference TrivediT1]);
$s\geqslant 1$
(see [Reference BrennerB] and [Reference TrivediT1]);(2) the HN data of
 $F^{s\ast }V_{p}$
are related to the HN data of
$F^{s\ast }V_{p}$
are related to the HN data of
 $V_{p}$
(see [Reference TrivediT2]);
$V_{p}$
(see [Reference TrivediT2]);(3) the restriction of the relative HN filtration of
 $V_{A}$
on
$V_{A}$
on
 $X_{A}$
(where
$X_{A}$
(where
 $V_{A}$
is a spread of
$V_{A}$
is a spread of
 $V_{0}$
in char 0) remains the HN filtration of
$V_{0}$
in char 0) remains the HN filtration of
 $V_{p}$
for large
$V_{p}$
for large
 $p$
(see [Reference MaruyamaMar]).
$p$
(see [Reference MaruyamaMar]).
In particular, for a pair
![]() $(R,I)$
, where
$(R,I)$
, where
![]() $\text{char}~R=p>0$
, with the associated syzygy bundle
$\text{char}~R=p>0$
, with the associated syzygy bundle
![]() $V$
(as above), the proof uses the comparison of
$V$
(as above), the proof uses the comparison of
![]() $\ell (R/I^{[p^{s}]})$
with the HN data of the syzygy bundle
$\ell (R/I^{[p^{s}]})$
with the HN data of the syzygy bundle
![]() $V$
and the other well behaved invariants of (
$V$
and the other well behaved invariants of (
![]() $R$
,
$R$
,
![]() $I$
) (which have well defined notion in all characteristics and are well behaved vis-a-vis reduction mod
$I$
) (which have well defined notion in all characteristics and are well behaved vis-a-vis reduction mod
![]() $p$
).
$p$
).
However, note that (3) is valid for
![]() $\dim R\geqslant 2$
, and (2) also holds for
$\dim R\geqslant 2$
, and (2) also holds for
![]() $\dim R\geqslant 3$
(proved relatively recently in [Reference TrivediT3]). However, (1) does not seem to hold in higher dimension, due to the existence of cohomologies other than
$\dim R\geqslant 3$
(proved relatively recently in [Reference TrivediT3]). However, (1) does not seem to hold in higher dimension, due to the existence of cohomologies other than
![]() $H^{0}(-)$
and
$H^{0}(-)$
and
![]() $H^{1}(-)$
(therefore, one cannot use anymore the semistability property of a vector bundle to compute
$H^{1}(-)$
(therefore, one cannot use anymore the semistability property of a vector bundle to compute
![]() $h^{0}$
of almost all of its twists, by powers of a very ample line bundle).
$h^{0}$
of almost all of its twists, by powers of a very ample line bundle).
In this paper, we approach the problem by a completely different method (see Corollary 2.12), comparing directly
![]() $(1/(p^{n})^{d})\ell (R/I^{[p^{n}]})$
and
$(1/(p^{n})^{d})\ell (R/I^{[p^{n}]})$
and
![]() $(1/(p^{n+1})^{d})\ell (R/I^{[p^{n+1}]})$
, for
$(1/(p^{n+1})^{d})\ell (R/I^{[p^{n+1}]})$
, for
![]() $n\geqslant 1$
, taking into account that both are graded.
$n\geqslant 1$
, taking into account that both are graded.
For this, we phrase the problem in a more general setting: by the theory of the Hilbert–Kunz (HK) density function (which was introduced and developed in [Reference TrivediT4]), for a pair
![]() $(R_{p},I_{p})$
, where
$(R_{p},I_{p})$
, where
![]() $R_{p}$
is a domain of
$R_{p}$
is a domain of
![]() $\text{char}~p>0$
, there exists a sequence of functions
$\text{char}~p>0$
, there exists a sequence of functions
![]() $\{f_{n}(R_{p},I_{p}):[0,\infty )\longrightarrow \mathbb{R}\}_{n}$
such that
$\{f_{n}(R_{p},I_{p}):[0,\infty )\longrightarrow \mathbb{R}\}_{n}$
such that
and
where the map
is called the HK density function of
![]() $(R_{p},I_{p})$
(the existence and properties of the limit defining
$(R_{p},I_{p})$
(the existence and properties of the limit defining
![]() $f_{R_{p},I_{p}}$
are proved in [Reference TrivediT4]). We show here that, for each
$f_{R_{p},I_{p}}$
are proved in [Reference TrivediT4]). We show here that, for each
![]() $x\in [1,\infty )$
,
$x\in [1,\infty )$
,
 $$\begin{eqnarray}\displaystyle f_{R,I}^{\infty }(x) & := & \displaystyle \lim _{p\rightarrow \infty }\lim _{n\rightarrow \infty }f_{n}(R_{p},I_{p})(x)\quad \text{exists}\quad \nonumber\\ \displaystyle & & \displaystyle \;\Longleftrightarrow \;\quad \lim _{p\rightarrow \infty }f_{m}(R_{p},I_{p})(x)\quad \text{exists},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{R,I}^{\infty }(x) & := & \displaystyle \lim _{p\rightarrow \infty }\lim _{n\rightarrow \infty }f_{n}(R_{p},I_{p})(x)\quad \text{exists}\quad \nonumber\\ \displaystyle & & \displaystyle \;\Longleftrightarrow \;\quad \lim _{p\rightarrow \infty }f_{m}(R_{p},I_{p})(x)\quad \text{exists},\nonumber\end{eqnarray}$$
for any fixed
![]() $m\geqslant d-1$
, where
$m\geqslant d-1$
, where
![]() $d-1=\dim \text{Proj}~R$
. Moreover, if it exists, then
$d-1=\dim \text{Proj}~R$
. Moreover, if it exists, then
The main point (Proposition 2.11) is to give a bound on the difference
![]() $\Vert f_{n}(R_{p},I_{p})-f_{n+1}(R_{p},I_{p})\Vert$
, in terms of a power of
$\Vert f_{n}(R_{p},I_{p})-f_{n+1}(R_{p},I_{p})\Vert$
, in terms of a power of
![]() $p$
and invariants that are well behaved under reduction mod
$p$
and invariants that are well behaved under reduction mod
![]() $p$
, where
$p$
, where
![]() $\Vert g\Vert :=\sup \{g(x)\mid x\in [1,\infty )\}$
is the
$\Vert g\Vert :=\sup \{g(x)\mid x\in [1,\infty )\}$
is the
![]() $L^{\infty }$
norm. Since the union of the support of all
$L^{\infty }$
norm. Since the union of the support of all
![]() $f_{n}$
is contained in a compact interval, a similar bound (Corollary 2.12) holds for the difference
$f_{n}$
is contained in a compact interval, a similar bound (Corollary 2.12) holds for the difference
![]() $|\ell (R/I^{[p^{n}]})/(p^{n})^{d}-\ell (R/I^{[p^{n+1}]})/(p^{n+1})^{d}|$
. More precisely, we prove the following theorem.
$|\ell (R/I^{[p^{n}]})/(p^{n})^{d}-\ell (R/I^{[p^{n+1}]})/(p^{n+1})^{d}|$
. More precisely, we prove the following theorem.
Theorem 1.1. Let
![]() $R$
be a standard graded domain of dimension
$R$
be a standard graded domain of dimension
![]() $d\geqslant 2$
, over an algebraically closed field
$d\geqslant 2$
, over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
. Let
$0$
. Let
![]() $I\subset R$
be a homogeneous ideal of finite colength. Let
$I\subset R$
be a homogeneous ideal of finite colength. Let
![]() $(A,R_{A},I_{A})$
be a spread (see Definition 3.2 and Notations 3.3). Then, for a closed point
$(A,R_{A},I_{A})$
be a spread (see Definition 3.2 and Notations 3.3). Then, for a closed point
![]() $s\in \text{Spec}(A)$
, let the function
$s\in \text{Spec}(A)$
, let the function
![]() $f_{n}(R_{s},I_{s})(x):[1,\infty )\longrightarrow [0,\infty )$
be given by
$f_{n}(R_{s},I_{s})(x):[1,\infty )\longrightarrow [0,\infty )$
be given by
 $$\begin{eqnarray}f_{n}(R_{s},I_{s})(x)=\frac{1}{q^{d-1}}\ell \left(\frac{R_{s}}{I_{s}^{[q]}}\right)_{\lfloor xq\rfloor },\end{eqnarray}$$
$$\begin{eqnarray}f_{n}(R_{s},I_{s})(x)=\frac{1}{q^{d-1}}\ell \left(\frac{R_{s}}{I_{s}^{[q]}}\right)_{\lfloor xq\rfloor },\end{eqnarray}$$
where
![]() $q=p_{s}^{n}$
, for
$q=p_{s}^{n}$
, for
![]() $p_{s}=\text{char}~k(s)$
, and
$p_{s}=\text{char}~k(s)$
, and
![]() $\lfloor y\rfloor$
denotes the largest integer
$\lfloor y\rfloor$
denotes the largest integer
![]() ${\leqslant}y$
and
${\leqslant}y$
and
![]() $\ell (R_{s}/I_{s}^{[q]})_{m}$
denotes the length of the
$\ell (R_{s}/I_{s}^{[q]})_{m}$
denotes the length of the
![]() $m$
th graded piece of the ring
$m$
th graded piece of the ring
![]() $R_{s}/I_{s}^{[q]}$
.
$R_{s}/I_{s}^{[q]}$
.
Let the HK density function of
![]() $(R_{s},I_{s})$
be given by
$(R_{s},I_{s})$
be given by
Let
![]() $s_{0}\in \text{Spec}~Q(A)$
denote the generic point of
$s_{0}\in \text{Spec}~Q(A)$
denote the generic point of
![]() $\text{Spec}(A)$
. Then, we have the following.
$\text{Spec}(A)$
. Then, we have the following.
(1) There exist a constant
 $C$
(given in terms of invariants of
$C$
(given in terms of invariants of
 $(R_{s_{0}},I_{s_{0}})$
of the generic fiber) and an open dense subset
$(R_{s_{0}},I_{s_{0}})$
of the generic fiber) and an open dense subset
 $\text{Spec}(A^{\prime })$
of
$\text{Spec}(A^{\prime })$
of
 $\text{Spec}(A)$
such that for every closed point
$\text{Spec}(A)$
such that for every closed point
 $s\in \text{Spec}(A^{\prime })$
and
$s\in \text{Spec}(A^{\prime })$
and
 $n\geqslant 1$
, where
$n\geqslant 1$
, where $$\begin{eqnarray}\Vert f_{n}(R_{s},I_{s})-f_{n+1}(R_{s},I_{s})\Vert <C/p_{s}^{n-d+2},\end{eqnarray}$$
$$\begin{eqnarray}\Vert f_{n}(R_{s},I_{s})-f_{n+1}(R_{s},I_{s})\Vert <C/p_{s}^{n-d+2},\end{eqnarray}$$
 $p_{s}=\text{char}~k(s)$
. In particular, for any
$p_{s}=\text{char}~k(s)$
. In particular, for any
 $m\geqslant d-1$
,
$m\geqslant d-1$
,  $$\begin{eqnarray}\lim _{p_{s}\rightarrow \infty }\Vert f_{m}(R_{s},I_{s})-f_{R_{s},I_{s}}\Vert =0.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{p_{s}\rightarrow \infty }\Vert f_{m}(R_{s},I_{s})-f_{R_{s},I_{s}}\Vert =0.\end{eqnarray}$$
(2) There exist a constant
 $C_{1}$
(given in terms of invariants of
$C_{1}$
(given in terms of invariants of
 $(R_{s_{0}},I_{s_{0}})$
) and an open dense subset
$(R_{s_{0}},I_{s_{0}})$
) and an open dense subset
 $\text{Spec}(A^{\prime })$
of
$\text{Spec}(A^{\prime })$
of
 $\text{Spec}(A)$
, such that for every closed point
$\text{Spec}(A)$
, such that for every closed point
 $s\in \text{Spec}(A^{\prime })$
and
$s\in \text{Spec}(A^{\prime })$
and
 $n\geqslant 1$
, we have
$n\geqslant 1$
, we have  $$\begin{eqnarray}\left|\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n}]}}\right)-\frac{1}{p_{s}^{(n+1)d}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n+1}]}}\right)\right|\leqslant \frac{C_{1}}{p_{s}^{n-d+2}}.\end{eqnarray}$$
$$\begin{eqnarray}\left|\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n}]}}\right)-\frac{1}{p_{s}^{(n+1)d}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n+1}]}}\right)\right|\leqslant \frac{C_{1}}{p_{s}^{n-d+2}}.\end{eqnarray}$$
(3) For any
 $m\geqslant d-1$
,
$m\geqslant d-1$
,  $$\begin{eqnarray}\lim _{p_{s}\rightarrow \infty }\left[\frac{1}{p_{s}^{md}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{m}]}}\right)-e_{HK}(R_{s},I_{s})\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{p_{s}\rightarrow \infty }\left[\frac{1}{p_{s}^{md}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{m}]}}\right)-e_{HK}(R_{s},I_{s})\right]=0.\end{eqnarray}$$
As a result, we have the following corollary.
Corollary 1.2. Let
![]() $R$
be a standard graded domain and a finitely generated
$R$
be a standard graded domain and a finitely generated
![]() $\mathbb{Z}$
-algebra of characteristic
$\mathbb{Z}$
-algebra of characteristic
![]() $0$
, and let
$0$
, and let
![]() $I\subset R$
be a homogeneous ideal of finite colength, such that for almost all
$I\subset R$
be a homogeneous ideal of finite colength, such that for almost all
![]() $p$
, the fiber over
$p$
, the fiber over
![]() $p$
,
$p$
,
![]() $R_{p}:=R\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
, is a standard graded ring of dimension
$R_{p}:=R\otimes _{\mathbb{Z}}\mathbb{Z}/p\mathbb{Z}$
, is a standard graded ring of dimension
![]() $d$
, which is geometrically integral, and
$d$
, which is geometrically integral, and
![]() $I_{p}\subset R_{p}$
is a homogeneous ideal of finite colength. Then, we have the following.
$I_{p}\subset R_{p}$
is a homogeneous ideal of finite colength. Then, we have the following.
(1) There exists a constant
 $C_{1}$
given in terms of invariants of
$C_{1}$
given in terms of invariants of
 $R$
and
$R$
and
 $I$
such that, for
$I$
such that, for
 $n\geqslant 1$
, we have
$n\geqslant 1$
, we have  $$\begin{eqnarray}\left|\frac{1}{p^{nd}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{n}]}}\right)-\frac{1}{p^{(n+1)d}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{n+1}]}}\right)\right|\leqslant \frac{C_{1}}{p^{n-d+2}}.\end{eqnarray}$$
$$\begin{eqnarray}\left|\frac{1}{p^{nd}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{n}]}}\right)-\frac{1}{p^{(n+1)d}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{n+1}]}}\right)\right|\leqslant \frac{C_{1}}{p^{n-d+2}}.\end{eqnarray}$$
(2) For any fixed
 $m\geqslant d-1$
, In particular, for any fixed
$m\geqslant d-1$
, In particular, for any fixed $$\begin{eqnarray}\lim _{p\rightarrow \infty }\left[e_{HK}(R_{p},I_{p})-\frac{1}{p^{md}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{m}]}}\right)\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{p\rightarrow \infty }\left[e_{HK}(R_{p},I_{p})-\frac{1}{p^{md}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{m}]}}\right)\right]=0.\end{eqnarray}$$
 $m\geqslant d-1$
,
$m\geqslant d-1$
,  $$\begin{eqnarray}\displaystyle e_{HK}^{\infty }(R,I) & := & \displaystyle \lim _{p\rightarrow \infty }e_{HK}(R_{p},I_{p})\quad \text{exists}\quad \nonumber\\ \displaystyle & & \displaystyle \;\Longleftrightarrow \;\quad \lim _{p\rightarrow \infty }\frac{1}{p^{md}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{m}]}}\right)\quad \text{exists}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{HK}^{\infty }(R,I) & := & \displaystyle \lim _{p\rightarrow \infty }e_{HK}(R_{p},I_{p})\quad \text{exists}\quad \nonumber\\ \displaystyle & & \displaystyle \;\Longleftrightarrow \;\quad \lim _{p\rightarrow \infty }\frac{1}{p^{md}}\ell \left(\frac{R_{p}}{I_{p}^{[p^{m}]}}\right)\quad \text{exists}.\nonumber\end{eqnarray}$$
In particular, the last assertion of the above corollary answers the abovementioned question of [Reference Brenner, Li and MillerBLM] affirmatively, for all
![]() $(R,I)$
, where
$(R,I)$
, where
![]() $R$
is a standard graded domain and
$R$
is a standard graded domain and
![]() $I\subset R$
is a graded ideal of finite colength.
$I\subset R$
is a graded ideal of finite colength.
Moreover, the proof, even in the case of dimension 2 (unlike the proof in [Reference Brenner, Li and MillerBLM]), does not rely on earlier results of [Reference BrennerB], [Reference TrivediT1], and [Reference TrivediT2]. In particular, since we do not use HN filtrations, we do not need a normality hypothesis on the ring
![]() $R$
.
$R$
.
Remark 1.3. If
![]() $e_{HK}^{\infty }(R,I)$
exists for a pair
$e_{HK}^{\infty }(R,I)$
exists for a pair
![]() $(R,I)$
, whenever
$(R,I)$
, whenever
![]() $R$
is a standard graded domain, defined over an algebraically closed field of characteristic 0, then one can check that
$R$
is a standard graded domain, defined over an algebraically closed field of characteristic 0, then one can check that
![]() $e_{HK}^{\infty }(R,I)$
exists for any pair
$e_{HK}^{\infty }(R,I)$
exists for any pair
![]() $(R,I)$
, where
$(R,I)$
, where
![]() $R$
is a standard graded ring over a field
$R$
is a standard graded ring over a field
![]() $k$
of characteristic 0. Let
$k$
of characteristic 0. Let
![]() $\bar{R}=R\otimes _{k}\bar{k}$
. Let
$\bar{R}=R\otimes _{k}\bar{k}$
. Let
![]() $\{q_{1},\ldots ,q_{r}\}=\{q\in \text{Ass}(\bar{R})\mid \dim \bar{R}/q=\dim R\}$
; then, we have a spread
$\{q_{1},\ldots ,q_{r}\}=\{q\in \text{Ass}(\bar{R})\mid \dim \bar{R}/q=\dim R\}$
; then, we have a spread
![]() $(A,\bar{R}_{A},\bar{I}_{A})$
of
$(A,\bar{R}_{A},\bar{I}_{A})$
of
![]() $(\bar{R},\bar{I})$
such that
$(\bar{R},\bar{I})$
such that
![]() $\{q_{1s},\ldots ,q_{rs}\}=\{q_{s}\in \text{Ass}(\bar{R}_{s})\mid \dim \bar{R}_{s}/q_{s}=\dim \bar{R}_{s}\}$
(here,
$\{q_{1s},\ldots ,q_{rs}\}=\{q_{s}\in \text{Ass}(\bar{R}_{s})\mid \dim \bar{R}_{s}/q_{s}=\dim \bar{R}_{s}\}$
(here,
![]() $q_{is}=q_{i}\otimes _{k}\bar{k(s)}\subset \bar{R}$
). Moreover, for each
$q_{is}=q_{i}\otimes _{k}\bar{k(s)}\subset \bar{R}$
). Moreover, for each
![]() $i$
,
$i$
,
![]() $\ell ((\bar{R}_{s})q_{is})=l_{i}$
, a constant independent of
$\ell ((\bar{R}_{s})q_{is})=l_{i}$
, a constant independent of
![]() $s$
. This implies that
$s$
. This implies that
which implies
 $$\begin{eqnarray}\displaystyle \lim _{p_{s}\rightarrow \infty }e_{HK}(\bar{R}_{s},\bar{I}_{s}) & = & \displaystyle \mathop{\sum }_{i=1}^{r}l_{i}\lim _{p_{s}\rightarrow \infty }e_{HK}\left(\frac{\bar{R}_{s}}{q_{is}},\frac{\bar{I}_{s}+q_{is}}{q_{is}}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{r}l_{i}e_{HK}^{\infty }\left(\frac{\bar{R}}{q_{i}},\frac{\bar{I}+q_{i}}{q_{i}}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \lim _{p_{s}\rightarrow \infty }e_{HK}(\bar{R}_{s},\bar{I}_{s}) & = & \displaystyle \mathop{\sum }_{i=1}^{r}l_{i}\lim _{p_{s}\rightarrow \infty }e_{HK}\left(\frac{\bar{R}_{s}}{q_{is}},\frac{\bar{I}_{s}+q_{is}}{q_{is}}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=1}^{r}l_{i}e_{HK}^{\infty }\left(\frac{\bar{R}}{q_{i}},\frac{\bar{I}+q_{i}}{q_{i}}\right).\nonumber\end{eqnarray}$$
Hence, in this situation, one can define
In Section 4, we study some properties of
![]() $f_{R,I}^{\infty }$
(when it exists), and prove that
$f_{R,I}^{\infty }$
(when it exists), and prove that
![]() $f_{R,I}^{\infty }$
behaves well under Segre product (Propositions 4.3 and 4.4). In the case of nonsingular projective curves (Theorem 4.6), the function
$f_{R,I}^{\infty }$
behaves well under Segre product (Propositions 4.3 and 4.4). In the case of nonsingular projective curves (Theorem 4.6), the function
![]() $f_{R_{s},I_{s}}-f_{R,I}^{\infty }$
is nonnegative, continuous, and characterizes the behavior of the HN filtration of the syzygy bundle of the curve, reduction mod
$f_{R_{s},I_{s}}-f_{R,I}^{\infty }$
is nonnegative, continuous, and characterizes the behavior of the HN filtration of the syzygy bundle of the curve, reduction mod
![]() $\text{char}~k(s)$
. Hence,
$\text{char}~k(s)$
. Hence,
![]() $f_{(S_{1}\#\cdots \#S_{n})_{p}}-f_{S_{1}\#\cdots \#S_{n}}^{\infty }=0$
if and only if the HN filtrations of the syzygy bundles of
$f_{(S_{1}\#\cdots \#S_{n})_{p}}-f_{S_{1}\#\cdots \#S_{n}}^{\infty }=0$
if and only if the HN filtrations of the syzygy bundles of
![]() $\text{Proj}~S_{i}$
are the strong HN filtrations reduction mod
$\text{Proj}~S_{i}$
are the strong HN filtrations reduction mod
![]() $p$
, for all
$p$
, for all
![]() $i$
.
$i$
.
We give an example to show that, for an arbitrary Segre product of plane trinomial curves, the function
![]() $f_{(S_{1}\#\cdots \#S_{n})_{p}}=f_{S_{1}\#\cdots \#S_{n}}^{\infty }$
, for a Zariski dense set of primes. Moreover, the function
$f_{(S_{1}\#\cdots \#S_{n})_{p}}=f_{S_{1}\#\cdots \#S_{n}}^{\infty }$
, for a Zariski dense set of primes. Moreover, the function
![]() $f_{(S_{1}\#\cdots \#S_{n})_{p}}\neq f_{S_{1}\#\cdots \#S_{n}}^{\infty }$
, for a Zariski dense set of primes, if one of the trinomials is symmetric. It is easy to check that if
$f_{(S_{1}\#\cdots \#S_{n})_{p}}\neq f_{S_{1}\#\cdots \#S_{n}}^{\infty }$
, for a Zariski dense set of primes, if one of the trinomials is symmetric. It is easy to check that if
![]() $f_{R,I}^{\infty }$
exists (in
$f_{R,I}^{\infty }$
exists (in
![]() $L^{\infty }$
norm), then
$L^{\infty }$
norm), then
![]() $e_{HK}^{\infty }(R,I)$
exists. One can ask the converse, that is, the following question.
$e_{HK}^{\infty }(R,I)$
exists. One can ask the converse, that is, the following question.
Question. Does the existence of
![]() $e_{HK}^{\infty }(R,I)$
imply the existence of
$e_{HK}^{\infty }(R,I)$
imply the existence of
![]() $f_{R,I}^{\infty }$
?
$f_{R,I}^{\infty }$
?
By Proposition 4.3, an affirmative answer to this question will imply the existence of the
![]() $e_{HK}^{\infty }$
for Segre products of the rings for which
$e_{HK}^{\infty }$
for Segre products of the rings for which
![]() $e_{HK}^{\infty }$
exist.
$e_{HK}^{\infty }$
exist.
The author would like to thank the referee for carefully reading the paper, and for the comments which helped in improving the exposition.
2 A key proposition
Throughout this section,
![]() $R$
is a Noetherian standard graded integral domain of dimension
$R$
is a Noetherian standard graded integral domain of dimension
![]() $d\geqslant 2$
over an algebraically closed field
$d\geqslant 2$
over an algebraically closed field
![]() $k$
of
$k$
of
![]() $\text{char}~p>0$
,
$\text{char}~p>0$
,
![]() $I$
is a homogeneous ideal of
$I$
is a homogeneous ideal of
![]() $R$
such that
$R$
such that
![]() $\ell (R/I)<\infty$
. Let
$\ell (R/I)<\infty$
. Let
![]() $h_{1},\ldots ,h_{\unicode[STIX]{x1D707}}$
be a set of homogeneous generators of
$h_{1},\ldots ,h_{\unicode[STIX]{x1D707}}$
be a set of homogeneous generators of
![]() $I$
of degrees
$I$
of degrees
![]() $d_{1},\ldots ,d_{\unicode[STIX]{x1D707}}$
, respectively. Moreover,
$d_{1},\ldots ,d_{\unicode[STIX]{x1D707}}$
, respectively. Moreover,
![]() $\mathbf{m}$
denotes the graded maximal ideal of
$\mathbf{m}$
denotes the graded maximal ideal of
![]() $R$
.
$R$
.
Let
![]() $X=\text{Proj}~R$
; then, we have an associated canonical short exact sequence of locally free sheaves of
$X=\text{Proj}~R$
; then, we have an associated canonical short exact sequence of locally free sheaves of
![]() ${\mathcal{O}}_{X}$
-modules (moreover, the sequence is locally split exact),
${\mathcal{O}}_{X}$
-modules (moreover, the sequence is locally split exact),
where
![]() ${\mathcal{O}}_{X}(1-d_{i})\longrightarrow {\mathcal{O}}_{X}(1)$
is given by the multiplication by the element
${\mathcal{O}}_{X}(1-d_{i})\longrightarrow {\mathcal{O}}_{X}(1)$
is given by the multiplication by the element
![]() $h_{i}$
.
$h_{i}$
.
For a coherent sheaf
![]() ${\mathcal{Q}}$
of
${\mathcal{Q}}$
of
![]() ${\mathcal{O}}_{X}$
-modules, the sequence of
${\mathcal{O}}_{X}$
-modules, the sequence of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
is exact as the short exact sequence (2) is locally split as
![]() ${\mathcal{O}}_{X}$
-modules (as usual,
${\mathcal{O}}_{X}$
-modules (as usual,
![]() $q=p^{n}$
, and
$q=p^{n}$
, and
![]() $F^{n}$
is the
$F^{n}$
is the
![]() $n$
th iterate of the absolute Frobenius morphism). Therefore, we have a long exact sequence of cohomologies
$n$
th iterate of the absolute Frobenius morphism). Therefore, we have a long exact sequence of cohomologies
 $$\begin{eqnarray}\displaystyle 0 & \longrightarrow & \displaystyle H^{0}(X,F^{n\ast }V\otimes {\mathcal{Q}}(m))\nonumber\\ \displaystyle & \longrightarrow & \displaystyle \oplus _{i}H^{0}(X,{\mathcal{Q}}(q-qd_{i}+m))\stackrel{\unicode[STIX]{x1D719}_{m,q}({\mathcal{Q}})}{\rightarrow }H^{0}(X,{\mathcal{Q}}(q+m))\nonumber\\ \displaystyle & \longrightarrow & \displaystyle H^{1}(X,F^{n\ast }V\otimes {\mathcal{Q}}(m))\longrightarrow \cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \longrightarrow & \displaystyle H^{0}(X,F^{n\ast }V\otimes {\mathcal{Q}}(m))\nonumber\\ \displaystyle & \longrightarrow & \displaystyle \oplus _{i}H^{0}(X,{\mathcal{Q}}(q-qd_{i}+m))\stackrel{\unicode[STIX]{x1D719}_{m,q}({\mathcal{Q}})}{\rightarrow }H^{0}(X,{\mathcal{Q}}(q+m))\nonumber\\ \displaystyle & \longrightarrow & \displaystyle H^{1}(X,F^{n\ast }V\otimes {\mathcal{Q}}(m))\longrightarrow \cdots \,,\end{eqnarray}$$
for
![]() $m\geqslant 0$
and
$m\geqslant 0$
and
![]() $q=p^{n}$
.
$q=p^{n}$
.
We recall the definition of (Castelnuovo–Mumford) regularity.
Definition 2.1. Let
![]() ${\mathcal{Q}}$
be a coherent sheaf of
${\mathcal{Q}}$
be a coherent sheaf of
![]() ${\mathcal{O}}_{X}$
-modules, and let
${\mathcal{O}}_{X}$
-modules, and let
![]() ${\mathcal{O}}_{X}(1)$
be a very ample line bundle on
${\mathcal{O}}_{X}(1)$
be a very ample line bundle on
![]() $X$
. For
$X$
. For
![]() $\tilde{m}\in \mathbb{N}$
, we say that
$\tilde{m}\in \mathbb{N}$
, we say that
![]() ${\mathcal{Q}}$
is
${\mathcal{Q}}$
is
![]() $\tilde{m}$
-regular (or
$\tilde{m}$
-regular (or
![]() $\tilde{m}$
is a regularity number of
$\tilde{m}$
is a regularity number of
![]() ${\mathcal{Q}}$
) with respect to
${\mathcal{Q}}$
) with respect to
![]() ${\mathcal{O}}_{X}(1)$
if, for all
${\mathcal{O}}_{X}(1)$
if, for all
![]() $m\geqslant \tilde{m}$
,
$m\geqslant \tilde{m}$
,
(1) the canonical multiplication map
 $H^{0}(X,{\mathcal{Q}}(m))\otimes H^{0}(X,{\mathcal{O}}_{X}(1))\longrightarrow H^{0}(X,{\mathcal{Q}}(m+1))$
is surjective, and
$H^{0}(X,{\mathcal{Q}}(m))\otimes H^{0}(X,{\mathcal{O}}_{X}(1))\longrightarrow H^{0}(X,{\mathcal{Q}}(m+1))$
is surjective, and(2)
 $H^{i}(X,{\mathcal{Q}}(m-i))=0$
, for
$H^{i}(X,{\mathcal{Q}}(m-i))=0$
, for
 $i\geqslant 1$
.
$i\geqslant 1$
.
Notations 2.2.
(1) Let
be the Hilbert–Samuel polynomial of $$\begin{eqnarray}P_{(R,\mathbf{m})}(m)=\tilde{e}_{0}\binom{m+d-1}{d}-\tilde{e}_{1}\binom{m+d-2}{d-1}+\cdots +(-1)^{d}\tilde{e}_{d}\end{eqnarray}$$
$$\begin{eqnarray}P_{(R,\mathbf{m})}(m)=\tilde{e}_{0}\binom{m+d-1}{d}-\tilde{e}_{1}\binom{m+d-2}{d-1}+\cdots +(-1)^{d}\tilde{e}_{d}\end{eqnarray}$$
 $R$
with respect to the graded maximal ideal
$R$
with respect to the graded maximal ideal
 $\mathbf{m}$
. Therefore,
$\mathbf{m}$
. Therefore,  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m)) & = & \displaystyle \tilde{e}_{0}\binom{m+d-1}{d-1}-\tilde{e}_{1}\binom{m+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +(-1)^{d-1}\tilde{e}_{d-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m)) & = & \displaystyle \tilde{e}_{0}\binom{m+d-1}{d-1}-\tilde{e}_{1}\binom{m+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +(-1)^{d-1}\tilde{e}_{d-1}.\nonumber\end{eqnarray}$$
(2) Let
 $\bar{m}$
be a positive integer such that
$\bar{m}$
be a positive integer such that(a)
 $\bar{m}$
is a regularity number for
$\bar{m}$
is a regularity number for
 $(X,{\mathcal{O}}_{X}(1))$
, and
$(X,{\mathcal{O}}_{X}(1))$
, and(b)
 $R_{m}=h^{0}(X,{\mathcal{O}}_{X}(m))$
, for all
$R_{m}=h^{0}(X,{\mathcal{O}}_{X}(m))$
, for all
 $m\geqslant \bar{m}$
. In particular,
$m\geqslant \bar{m}$
. In particular,
 $\ell (R/\mathbf{m}^{m})=P_{(R,\mathbf{m})}(m)$
, for all
$\ell (R/\mathbf{m}^{m})=P_{(R,\mathbf{m})}(m)$
, for all
 $m\geqslant \bar{m}$
.
$m\geqslant \bar{m}$
.
(3) Let
 $l_{1}=h^{0}(X,{\mathcal{O}}_{X}(1))$
.
$l_{1}=h^{0}(X,{\mathcal{O}}_{X}(1))$
.(4) Let
 $n_{0}\geqslant 1$
be an integer such that
$n_{0}\geqslant 1$
be an integer such that
 $R_{n_{0}}\subseteq I$
, where
$R_{n_{0}}\subseteq I$
, where
 $R=\oplus _{n\geqslant 0}R_{n}$
.
$R=\oplus _{n\geqslant 0}R_{n}$
.(5) We denote
 $\dim _{k}\text{Coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{Q}})$
by
$\dim _{k}\text{Coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{Q}})$
by
 $\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{Q}})$
.
$\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{Q}})$
.
Remark 2.3.
(1) The canonical map
 $\oplus _{m}{R_{m}\longrightarrow \oplus }_{m}H^{0}(X,{\mathcal{O}}_{X}(m))$
is injective, as
$\oplus _{m}{R_{m}\longrightarrow \oplus }_{m}H^{0}(X,{\mathcal{O}}_{X}(m))$
is injective, as
 $R$
is an integral domain.
$R$
is an integral domain.(2) For
 $m+q\geqslant m_{R}(q)=\bar{m}+n_{0}(\sum _{i}d_{i})q$
, we have
$m+q\geqslant m_{R}(q)=\bar{m}+n_{0}(\sum _{i}d_{i})q$
, we have
 $\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})=\ell (R/I^{[q]})_{m+q}=0$
, because
$\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})=\ell (R/I^{[q]})_{m+q}=0$
, because
 $m_{R}(q)=\bar{m}+n_{0}\unicode[STIX]{x1D707}q+n_{0}(\sum _{i}(d_{i}-1))q\Rightarrow q-qd_{i}+m\geqslant \bar{m},$
for all
$m_{R}(q)=\bar{m}+n_{0}\unicode[STIX]{x1D707}q+n_{0}(\sum _{i}(d_{i}-1))q\Rightarrow q-qd_{i}+m\geqslant \bar{m},$
for all
 $i$
. Hence, the map
$i$
. Hence, the map
 $\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})$
is the map
$\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})$
is the map
 $\oplus _{i}R_{q-qd_{i}+m}\longrightarrow R_{m+q}$
, where the map
$\oplus _{i}R_{q-qd_{i}+m}\longrightarrow R_{m+q}$
, where the map
 $R_{q-qd_{i}+m}\rightarrow R_{m+q}$
is given by multiplication by the element
$R_{q-qd_{i}+m}\rightarrow R_{m+q}$
is given by multiplication by the element
 $h_{i}^{q}$
. Therefore,
$h_{i}^{q}$
. Therefore,
 $\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})=\ell (R/I^{[q]})_{m+q}$
. Moreover, by the proof of Lemma 2.10, we have
$\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})=\ell (R/I^{[q]})_{m+q}$
. Moreover, by the proof of Lemma 2.10, we have
 $\ell (R/I^{[q]})_{m+q}=0$
, as
$\ell (R/I^{[q]})_{m+q}=0$
, as
 $m+q\geqslant \bar{m}+n_{0}\unicode[STIX]{x1D707}q$
.
$m+q\geqslant \bar{m}+n_{0}\unicode[STIX]{x1D707}q$
.(3) For
 $C_{R}=(\unicode[STIX]{x1D707})h^{0}(X,{\mathcal{O}}_{X}(\bar{m}))$
, we have (4)for all
$C_{R}=(\unicode[STIX]{x1D707})h^{0}(X,{\mathcal{O}}_{X}(\bar{m}))$
, we have (4)for all $$\begin{eqnarray}|\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}|\leqslant C_{R},\end{eqnarray}$$
$$\begin{eqnarray}|\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}|\leqslant C_{R},\end{eqnarray}$$
 $n,m\geqslant 0$
and
$n,m\geqslant 0$
and
 $q=p^{n}$
, because
$q=p^{n}$
, becauseif
 $m+q<\bar{m}$
, then If
$m+q<\bar{m}$
, then If $$\begin{eqnarray}\displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}| & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{O}}_{X}(m+q))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{O}}_{X}(\bar{m})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}| & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{O}}_{X}(m+q))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{O}}_{X}(\bar{m})).\nonumber\end{eqnarray}$$
 $m+q\geqslant \bar{m}$
, then
$m+q\geqslant \bar{m}$
, then
 $h^{0}(X,{\mathcal{O}}_{X}(m+q))=\ell (R_{m+q})$
, and therefore Now, if
$h^{0}(X,{\mathcal{O}}_{X}(m+q))=\ell (R_{m+q})$
, and therefore Now, if $$\begin{eqnarray}\displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}| & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\unicode[STIX]{x1D707}}|h^{0}(X,{\mathcal{O}}_{X}(q-qd_{i}+m))\nonumber\\ \displaystyle & & \displaystyle -\,\ell (R_{q-qd_{i}+m})|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}| & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\unicode[STIX]{x1D707}}|h^{0}(X,{\mathcal{O}}_{X}(q-qd_{i}+m))\nonumber\\ \displaystyle & & \displaystyle -\,\ell (R_{q-qd_{i}+m})|.\nonumber\end{eqnarray}$$
 $q-qd_{i}+m<\bar{m}$
, then
$q-qd_{i}+m<\bar{m}$
, then
 $\ell (R_{q-qd_{i}+m})\leqslant h^{0}(X,{\mathcal{O}}_{X}(q-qd_{i}+m))\leqslant h^{0}(X,{\mathcal{O}}_{X}(\bar{m}))$
, and if
$\ell (R_{q-qd_{i}+m})\leqslant h^{0}(X,{\mathcal{O}}_{X}(q-qd_{i}+m))\leqslant h^{0}(X,{\mathcal{O}}_{X}(\bar{m}))$
, and if
 $q-qd_{i}+m\geqslant \bar{m}$
, then
$q-qd_{i}+m\geqslant \bar{m}$
, then
 $R_{q-qd_{i}+m}=H^{0}(X,{\mathcal{O}}_{X}(q-qd_{i}+m))$
.
$R_{q-qd_{i}+m}=H^{0}(X,{\mathcal{O}}_{X}(q-qd_{i}+m))$
.Hence,
 $$\begin{eqnarray}|\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}|\leqslant \unicode[STIX]{x1D707}h^{0}(X,{\mathcal{O}}_{X}(\bar{m})).\end{eqnarray}$$
$$\begin{eqnarray}|\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\ell (R/I^{[q]})_{m+q}|\leqslant \unicode[STIX]{x1D707}h^{0}(X,{\mathcal{O}}_{X}(\bar{m})).\end{eqnarray}$$
Definition 2.4. Let
![]() ${\mathcal{Q}}$
be a coherent sheaf of
${\mathcal{Q}}$
be a coherent sheaf of
![]() ${\mathcal{O}}_{X}$
-modules of dimension
${\mathcal{O}}_{X}$
-modules of dimension
![]() $\bar{d}$
, and let
$\bar{d}$
, and let
![]() $\tilde{m}\geqslant 1$
be the least integer that is a regularity number for
$\tilde{m}\geqslant 1$
be the least integer that is a regularity number for
![]() ${\mathcal{Q}}$
with respect to
${\mathcal{Q}}$
with respect to
![]() ${\mathcal{O}}_{X}(1)$
. Then, we define
${\mathcal{O}}_{X}(1)$
. Then, we define
![]() $C_{0}({\mathcal{Q}})$
and
$C_{0}({\mathcal{Q}})$
and
![]() $D_{0}({\mathcal{Q}})$
as follows. Let
$D_{0}({\mathcal{Q}})$
as follows. Let
![]() $a_{1},\ldots ,a_{\bar{d}}\in H^{0}(X,{\mathcal{O}}_{X}(1))$
be such that we have a short exact sequence of
$a_{1},\ldots ,a_{\bar{d}}\in H^{0}(X,{\mathcal{O}}_{X}(1))$
be such that we have a short exact sequence of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
where
![]() ${\mathcal{Q}}_{d}={\mathcal{Q}}$
and
${\mathcal{Q}}_{d}={\mathcal{Q}}$
and
![]() ${\mathcal{Q}}_{i}={\mathcal{Q}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}$
, for
${\mathcal{Q}}_{i}={\mathcal{Q}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}$
, for
![]() $0\leqslant i<\bar{d}$
, with
$0\leqslant i<\bar{d}$
, with
![]() $\dim ~{\mathcal{Q}}_{i}=i$
. We define
$\dim ~{\mathcal{Q}}_{i}=i$
. We define
 $$\begin{eqnarray}\displaystyle & \displaystyle C_{0}({\mathcal{Q}})=\min \left\{\mathop{\sum }_{i=0}^{\bar{d}}h^{0}(X,{\mathcal{Q}}_{i})\mid a_{1},\ldots ,a_{\bar{d}}~\text{is a}~{\mathcal{Q}}\text{-}\text{sequence as above}\right\}, & \displaystyle \nonumber\\ \displaystyle & D_{0}({\mathcal{Q}})=h^{0}(X,{\mathcal{Q}}(\tilde{m}))+2(\bar{d}+1)\left(\max \{q_{0},q_{1},\ldots ,q_{\bar{d}}\}\right), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{0}({\mathcal{Q}})=\min \left\{\mathop{\sum }_{i=0}^{\bar{d}}h^{0}(X,{\mathcal{Q}}_{i})\mid a_{1},\ldots ,a_{\bar{d}}~\text{is a}~{\mathcal{Q}}\text{-}\text{sequence as above}\right\}, & \displaystyle \nonumber\\ \displaystyle & D_{0}({\mathcal{Q}})=h^{0}(X,{\mathcal{Q}}(\tilde{m}))+2(\bar{d}+1)\left(\max \{q_{0},q_{1},\ldots ,q_{\bar{d}}\}\right), & \displaystyle \nonumber\end{eqnarray}$$
where
is the Hilbert polynomial of
![]() ${\mathcal{Q}}$
.
${\mathcal{Q}}$
.
A more general version of the following lemma has been stated and proved in [Reference TrivediT4, Lemma 2.6]. Here, we state and prove a relevant part of it, for a self-contained treatment (avoiding additional complications).
Lemma 2.5. Let
![]() ${\mathcal{Q}}$
be a coherent sheaf of
${\mathcal{Q}}$
be a coherent sheaf of
![]() ${\mathcal{O}}_{X}$
-modules of dimension
${\mathcal{O}}_{X}$
-modules of dimension
![]() $\bar{d}$
. Let
$\bar{d}$
. Let
![]() $P$
be a locally free sheaf of
$P$
be a locally free sheaf of
![]() ${\mathcal{O}}_{X}$
-modules that fits into a short exact sequence of locally free sheaves of
${\mathcal{O}}_{X}$
-modules that fits into a short exact sequence of locally free sheaves of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
Then, for
![]() $\tilde{\unicode[STIX]{x1D707}}=\text{rank}(P)+\text{rank}(P^{\prime \prime })$
and for all
$\tilde{\unicode[STIX]{x1D707}}=\text{rank}(P)+\text{rank}(P^{\prime \prime })$
and for all
![]() $n,m\geqslant 0$
, we have
$n,m\geqslant 0$
, we have
and
Proof. Let
![]() $\tilde{m}$
be a regularity number for
$\tilde{m}$
be a regularity number for
![]() ${\mathcal{Q}}$
; then, by Definition 2.4, we have
${\mathcal{Q}}$
; then, by Definition 2.4, we have
Let
![]() ${\mathcal{Q}}_{\bar{d}}={\mathcal{Q}}$
. Let
${\mathcal{Q}}_{\bar{d}}={\mathcal{Q}}$
. Let
![]() $a_{\bar{d}},\ldots ,a_{1}\in H^{0}(X,{\mathcal{O}}_{X}(1))$
, with the exact sequence of
$a_{\bar{d}},\ldots ,a_{1}\in H^{0}(X,{\mathcal{O}}_{X}(1))$
, with the exact sequence of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
where
![]() ${\mathcal{Q}}_{i}={\mathcal{Q}}_{\bar{d}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}_{\bar{d}}$
, for
${\mathcal{Q}}_{i}={\mathcal{Q}}_{\bar{d}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}_{\bar{d}}$
, for
![]() $0\leqslant i\leqslant \bar{d}$
, and realizing the minimal value
$0\leqslant i\leqslant \bar{d}$
, and realizing the minimal value
![]() $C_{0}({\mathcal{Q}})$
. Now, by the exact sequence (5), we have the following short exact sequence of
$C_{0}({\mathcal{Q}})$
. Now, by the exact sequence (5), we have the following short exact sequence of
![]() ${\mathcal{O}}_{X}$
-sheaves:
${\mathcal{O}}_{X}$
-sheaves:
This implies
![]() $H^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i}){\hookrightarrow}\oplus _{j}H^{0}(X,{\mathcal{Q}}_{i}(-qb_{j}))$
. Therefore,
$H^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i}){\hookrightarrow}\oplus _{j}H^{0}(X,{\mathcal{Q}}_{i}(-qb_{j}))$
. Therefore,
as
![]() $-b_{j}\leqslant 0$
. Since
$-b_{j}\leqslant 0$
. Since
![]() $F^{n\ast }P$
is a locally free sheaf of
$F^{n\ast }P$
is a locally free sheaf of
![]() ${\mathcal{O}}_{X}$
-modules, we have
${\mathcal{O}}_{X}$
-modules, we have
which is a short exact sequence of
![]() ${\mathcal{O}}_{X}$
-sheaves. Now, by induction on
${\mathcal{O}}_{X}$
-sheaves. Now, by induction on
![]() $i$
, we prove that, for
$i$
, we prove that, for
![]() $m\geqslant 1$
,
$m\geqslant 1$
,
For
![]() $i=0$
, the inequality holds as
$i=0$
, the inequality holds as
![]() $h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{0}(m))\leqslant (\tilde{\unicode[STIX]{x1D707}})h^{0}(X,{\mathcal{Q}}_{0})$
(as
$h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{0}(m))\leqslant (\tilde{\unicode[STIX]{x1D707}})h^{0}(X,{\mathcal{Q}}_{0})$
(as
![]() $\dim {\mathcal{Q}}_{0}=0$
).
$\dim {\mathcal{Q}}_{0}=0$
).
Now, for
![]() $m\geqslant 1$
, by the inequality (6) and by induction on
$m\geqslant 1$
, by the inequality (6) and by induction on
![]() $i$
, we have
$i$
, we have
 $$\begin{eqnarray}\displaystyle h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i}(m)) & {\leqslant} & \displaystyle h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i})+h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i-1}(1))\nonumber\\ \displaystyle & & \displaystyle +\cdots +h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i-1}(m))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (\tilde{\unicode[STIX]{x1D707}})h^{0}(X,{\mathcal{Q}}_{i})+\tilde{\unicode[STIX]{x1D707}}[h^{0}(X,{\mathcal{Q}}_{i-1})+\cdots +h^{0}(X,{\mathcal{Q}}_{0})]\nonumber\\ \displaystyle & & \displaystyle \times \,(1+2^{i-1}+\cdots +m^{i-1})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (\tilde{\unicode[STIX]{x1D707}})[h^{0}(X,{\mathcal{Q}}_{i})+\cdots +h^{0}(X,{\mathcal{Q}}_{0})]m^{i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i}(m)) & {\leqslant} & \displaystyle h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i})+h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i-1}(1))\nonumber\\ \displaystyle & & \displaystyle +\cdots +h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}_{i-1}(m))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (\tilde{\unicode[STIX]{x1D707}})h^{0}(X,{\mathcal{Q}}_{i})+\tilde{\unicode[STIX]{x1D707}}[h^{0}(X,{\mathcal{Q}}_{i-1})+\cdots +h^{0}(X,{\mathcal{Q}}_{0})]\nonumber\\ \displaystyle & & \displaystyle \times \,(1+2^{i-1}+\cdots +m^{i-1})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (\tilde{\unicode[STIX]{x1D707}})[h^{0}(X,{\mathcal{Q}}_{i})+\cdots +h^{0}(X,{\mathcal{Q}}_{0})]m^{i}.\nonumber\end{eqnarray}$$
This implies
for all
![]() $m\geqslant 1$
. Therefore, for all
$m\geqslant 1$
. Therefore, for all
![]() $0\leqslant i\leqslant \bar{d}$
and for all
$0\leqslant i\leqslant \bar{d}$
and for all
![]() $m\geqslant 0$
, we have
$m\geqslant 0$
, we have
![]() $h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}(m))\leqslant \tilde{\unicode[STIX]{x1D707}}C_{0}({\mathcal{Q}})(m^{\bar{d}}+1)$
. This proves the lemma.◻
$h^{0}(X,F^{n\ast }P\otimes {\mathcal{Q}}(m))\leqslant \tilde{\unicode[STIX]{x1D707}}C_{0}({\mathcal{Q}})(m^{\bar{d}}+1)$
. This proves the lemma.◻
Lemma 2.6. There exists a short exact sequence of coherent sheaves of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
where
![]() ${\mathcal{Q}}$
is a coherent sheaf of
${\mathcal{Q}}$
is a coherent sheaf of
![]() ${\mathcal{O}}_{X}$
-modules such that
${\mathcal{O}}_{X}$
-modules such that
![]() $\dim \text{supp}({\mathcal{Q}})<d-1$
.
$\dim \text{supp}({\mathcal{Q}})<d-1$
.
Proof. Note that
![]() $X=\text{Proj}~R$
, where
$X=\text{Proj}~R$
, where
![]() $R=\oplus _{n\geqslant 0}R_{n}$
, is a standard graded domain such that
$R=\oplus _{n\geqslant 0}R_{n}$
, is a standard graded domain such that
![]() $R_{0}$
is an algebraically closed field. Therefore, there exists a Noether normalization
$R_{0}$
is an algebraically closed field. Therefore, there exists a Noether normalization
which is an injective, finite separable graded map of degree 0 (as
![]() $k$
is an algebraically closed field). This induces a finite separable affine map
$k$
is an algebraically closed field). This induces a finite separable affine map
![]() $\unicode[STIX]{x1D70B}:X\longrightarrow \mathbb{P}_{k}^{d-1}=S$
.
$\unicode[STIX]{x1D70B}:X\longrightarrow \mathbb{P}_{k}^{d-1}=S$
.
Note that there is also an isomorphism
of
![]() ${\mathcal{O}}_{S}$
-modules, where
${\mathcal{O}}_{S}$
-modules, where
![]() $\sum \,n_{i}=p^{d-1}$
.
$\sum \,n_{i}=p^{d-1}$
.
Now, the isomorphism of
![]() $\unicode[STIX]{x1D702}$
implies that the map
$\unicode[STIX]{x1D702}$
implies that the map
is an isomorphism of
![]() ${\mathcal{O}}_{X}$
-sheaves. Since
${\mathcal{O}}_{X}$
-sheaves. Since
![]() $0\leqslant i\leqslant d-1$
, we also have an injective and generically isomorphic map of
$0\leqslant i\leqslant d-1$
, we also have an injective and generically isomorphic map of
![]() ${\mathcal{O}}_{X}$
-sheaves
${\mathcal{O}}_{X}$
-sheaves
Composing this map with
![]() $\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D702})$
gives an injective and generically isomorphic map of
$\unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D702})$
gives an injective and generically isomorphic map of
![]() ${\mathcal{O}}_{X}$
-sheaves
${\mathcal{O}}_{X}$
-sheaves
Since
![]() $\unicode[STIX]{x1D70B}$
is separable, there is a canonical map
$\unicode[STIX]{x1D70B}$
is separable, there is a canonical map
![]() $\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D70B}^{\ast }F_{\ast }{\mathcal{O}}_{S}\longrightarrow F_{\ast }{\mathcal{O}}_{X}$
, of sheaves of
$\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D70B}^{\ast }F_{\ast }{\mathcal{O}}_{S}\longrightarrow F_{\ast }{\mathcal{O}}_{X}$
, of sheaves of
![]() ${\mathcal{O}}_{X}$
-modules, which is generically isomorphic.
${\mathcal{O}}_{X}$
-modules, which is generically isomorphic.
Now, we have the composite map
which is generically an isomorphism. Hence,
![]() $\dim \text{Coker}(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC})<\dim X=d-1$
, and the map
$\dim \text{Coker}(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC})<\dim X=d-1$
, and the map
![]() $\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}:\oplus ^{p^{d-1}}{\mathcal{O}}_{X}(-d)\longrightarrow F_{\ast }{\mathcal{O}}_{X}$
is injective, as
$\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}:\oplus ^{p^{d-1}}{\mathcal{O}}_{X}(-d)\longrightarrow F_{\ast }{\mathcal{O}}_{X}$
is injective, as
![]() $X$
is an integral scheme. This proves the lemma.◻
$X$
is an integral scheme. This proves the lemma.◻
Lemma 2.7. Let
as in Lemma 2.6. Then, we have the following.
(1)
 ${\mathcal{Q}}$
is
${\mathcal{Q}}$
is
 $\tilde{m}$
-regular, where
$\tilde{m}$
-regular, where
 $\tilde{m}=\max \{\bar{m}+d,l_{1}-1\}$
, where
$\tilde{m}=\max \{\bar{m}+d,l_{1}-1\}$
, where
 $\bar{m}$
and
$\bar{m}$
and
 $l_{1}$
are as given in Notations 2.2.
$l_{1}$
are as given in Notations 2.2.(2) For a given
 $d$
, there exists a universal polynomial function, with rational coefficients,
$d$
, there exists a universal polynomial function, with rational coefficients,
 $\bar{P}_{1}^{d}(X_{0},\ldots ,X_{d-1},Y)$
(and hence independent of
$\bar{P}_{1}^{d}(X_{0},\ldots ,X_{d-1},Y)$
(and hence independent of
 $p$
), such that where we define (
$p$
), such that where we define ( $$\begin{eqnarray}2C_{0}({\mathcal{Q}})+D_{0}({\mathcal{Q}})\leqslant p^{d-1}\bar{P}_{1}^{d}(\tilde{e}_{0},\tilde{e}_{1},\ldots ,\tilde{e}_{d-1},\bar{m}),\end{eqnarray}$$
$$\begin{eqnarray}2C_{0}({\mathcal{Q}})+D_{0}({\mathcal{Q}})\leqslant p^{d-1}\bar{P}_{1}^{d}(\tilde{e}_{0},\tilde{e}_{1},\ldots ,\tilde{e}_{d-1},\bar{m}),\end{eqnarray}$$
 $\dim \text{supp}({\mathcal{Q}})=\bar{d}<d-1$
) and
$\dim \text{supp}({\mathcal{Q}})=\bar{d}<d-1$
) and $$\begin{eqnarray}\displaystyle C_{0}({\mathcal{Q}}) & = & \displaystyle \min \left\{\mathop{\sum }_{i=0}^{\bar{d}}h^{0}(X,{\mathcal{Q}}_{i})\mid a_{1},\ldots ,a_{\bar{d}}~\text{is a}~{\mathcal{Q}}\text{-}\text{sequence and}\right.\nonumber\\ \displaystyle & & \displaystyle \left.{\mathcal{Q}}_{i}={\mathcal{Q}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}\vphantom{\mathop{\sum }_{i=0}^{\bar{d}}}\right\}\nonumber\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle C_{0}({\mathcal{Q}}) & = & \displaystyle \min \left\{\mathop{\sum }_{i=0}^{\bar{d}}h^{0}(X,{\mathcal{Q}}_{i})\mid a_{1},\ldots ,a_{\bar{d}}~\text{is a}~{\mathcal{Q}}\text{-}\text{sequence and}\right.\nonumber\\ \displaystyle & & \displaystyle \left.{\mathcal{Q}}_{i}={\mathcal{Q}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}\vphantom{\mathop{\sum }_{i=0}^{\bar{d}}}\right\}\nonumber\end{eqnarray}$$
where $$\begin{eqnarray}D_{0}({\mathcal{Q}})=h^{0}(X,{\mathcal{Q}}(\tilde{m}))+2(\bar{d}+1)(\max \{q_{0},q_{1},\ldots ,q_{\bar{d}}\}),\end{eqnarray}$$
$$\begin{eqnarray}D_{0}({\mathcal{Q}})=h^{0}(X,{\mathcal{Q}}(\tilde{m}))+2(\bar{d}+1)(\max \{q_{0},q_{1},\ldots ,q_{\bar{d}}\}),\end{eqnarray}$$
 $q_{0},\ldots ,q_{\bar{d}}$
are the coefficients of the Hilbert polynomial
$q_{0},\ldots ,q_{\bar{d}}$
are the coefficients of the Hilbert polynomial
 $\unicode[STIX]{x1D712}(X,{\mathcal{Q}}(m))$
.
$\unicode[STIX]{x1D712}(X,{\mathcal{Q}}(m))$
.
Proof. (1) The above short exact sequence of
![]() ${\mathcal{O}}_{X}$
-sheaves gives a long exact sequence of cohomologies
${\mathcal{O}}_{X}$
-sheaves gives a long exact sequence of cohomologies
However,
![]() $h^{i}(X,{\mathcal{O}}_{X}(m-d-i))=0$
, for all
$h^{i}(X,{\mathcal{O}}_{X}(m-d-i))=0$
, for all
![]() $m\geqslant \bar{m}+d$
and
$m\geqslant \bar{m}+d$
and
![]() $i\geqslant 1$
, which implies that if
$i\geqslant 1$
, which implies that if
![]() $m\geqslant \bar{m}+d$
, then
$m\geqslant \bar{m}+d$
, then
![]() $h^{i}(X,{\mathcal{Q}}(m-i))=0$
, for
$h^{i}(X,{\mathcal{Q}}(m-i))=0$
, for
![]() $i\geqslant 1$
, and the canonical map
$i\geqslant 1$
, and the canonical map
is surjective. Moreover, the canonical map
is the same as the canonical map
which is surjective for
![]() $m\geqslant \tilde{m}$
. The map
$m\geqslant \tilde{m}$
. The map
![]() $f_{2m}$
fits into the following canonical diagram:
$f_{2m}$
fits into the following canonical diagram:
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}R_{mp}\otimes R_{1}^{[p]} & \longrightarrow & R_{mp+p}\\ \downarrow & & \downarrow \\ H^{0}(X,{\mathcal{O}}_{X}(mp))\otimes H^{0}(X,{\mathcal{O}}_{X}(1))^{[p]} & \stackrel{f_{2,m}}{\longrightarrow } & H^{0}(X,{\mathcal{O}}_{X}(mp+p)),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}R_{mp}\otimes R_{1}^{[p]} & \longrightarrow & R_{mp+p}\\ \downarrow & & \downarrow \\ H^{0}(X,{\mathcal{O}}_{X}(mp))\otimes H^{0}(X,{\mathcal{O}}_{X}(1))^{[p]} & \stackrel{f_{2,m}}{\longrightarrow } & H^{0}(X,{\mathcal{O}}_{X}(mp+p)),\end{array}\end{eqnarray}$$
where
![]() $H^{0}(X,{\mathcal{O}}_{X}(1))^{[p]}$
, as a set, is
$H^{0}(X,{\mathcal{O}}_{X}(1))^{[p]}$
, as a set, is
![]() $H^{0}(X,{\mathcal{O}}_{X}(1))$
, and the upper symbol
$H^{0}(X,{\mathcal{O}}_{X}(1))$
, and the upper symbol
![]() $^{[p]}$
indicates that the
$^{[p]}$
indicates that the
![]() $k$
-space structure is through the
$k$
-space structure is through the
![]() $p$
th power map of
$p$
th power map of
![]() $k$
, where the top horizontal map is surjective for
$k$
, where the top horizontal map is surjective for
![]() $m\geqslant l_{1}-1$
, and the right vertical map is identity as
$m\geqslant l_{1}-1$
, and the right vertical map is identity as
![]() $mp+p\geqslant \bar{m}$
. Now, the commutative diagram of canonical maps
$mp+p\geqslant \bar{m}$
. Now, the commutative diagram of canonical maps
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}H^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(m))\otimes H^{0}(X,{\mathcal{O}}_{X}(1)) & \longrightarrow & H^{0}(X,{\mathcal{Q}}(m))\otimes H^{0}(X,{\mathcal{O}}_{X}(1))\\ \downarrow f_{2,m} & & \downarrow \\ H^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(m+1)) & \stackrel{f_{1,m+1}}{\longrightarrow } & H^{0}(X,{\mathcal{Q}}(m+1))\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}H^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(m))\otimes H^{0}(X,{\mathcal{O}}_{X}(1)) & \longrightarrow & H^{0}(X,{\mathcal{Q}}(m))\otimes H^{0}(X,{\mathcal{O}}_{X}(1))\\ \downarrow f_{2,m} & & \downarrow \\ H^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(m+1)) & \stackrel{f_{1,m+1}}{\longrightarrow } & H^{0}(X,{\mathcal{Q}}(m+1))\end{array}\end{eqnarray}$$
implies that the second vertical map is surjective, for
![]() $m\geqslant \tilde{m}$
, as the maps
$m\geqslant \tilde{m}$
, as the maps
![]() $f_{2,m}$
and
$f_{2,m}$
and
![]() $f_{1,m+1}$
are surjective. This proves that
$f_{1,m+1}$
are surjective. This proves that
![]() ${\mathcal{Q}}$
is
${\mathcal{Q}}$
is
![]() $\tilde{m}$
-regular. Hence, the assertion (1).
$\tilde{m}$
-regular. Hence, the assertion (1).
(2) If
then, by Lemma A.1(1) (in the appendix, below),
where
![]() $P_{i}^{d}(X_{0},\ldots ,X_{i+1})$
is a universal polynomial function with rational coefficients.
$P_{i}^{d}(X_{0},\ldots ,X_{i+1})$
is a universal polynomial function with rational coefficients.
Now,
![]() ${\mathcal{Q}}$
is
${\mathcal{Q}}$
is
![]() $\tilde{m}$
-regular implies that, for
$\tilde{m}$
-regular implies that, for
![]() $0\leqslant i<d$
,
$0\leqslant i<d$
,
![]() ${\mathcal{Q}}_{i}:={\mathcal{Q}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}$
is
${\mathcal{Q}}_{i}:={\mathcal{Q}}/(a_{\bar{d}},\ldots ,a_{i+1}){\mathcal{Q}}$
is
![]() $\tilde{m}$
-regular, for any
$\tilde{m}$
-regular, for any
![]() ${\mathcal{Q}}$
-sequence
${\mathcal{Q}}$
-sequence
![]() $a_{1},\ldots ,a_{\bar{d}}\in H^{0}(X,{\mathcal{O}}_{X}(1))$
. Therefore, the short exact sequence of
$a_{1},\ldots ,a_{\bar{d}}\in H^{0}(X,{\mathcal{O}}_{X}(1))$
. Therefore, the short exact sequence of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
gives the short exact sequence of
![]() $k$
-vector spaces
$k$
-vector spaces
for
![]() $m\geqslant \tilde{m}$
. Hence,
$m\geqslant \tilde{m}$
. Hence,
 $$\begin{eqnarray}\displaystyle h^{0}(X,{\mathcal{Q}}_{i}) & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{Q}}_{i}(\tilde{m}))\leqslant \cdots \leqslant h^{0}(X,{\mathcal{Q}}(\tilde{m}))=\unicode[STIX]{x1D712}(X,{\mathcal{Q}}(\tilde{m}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \displaystyle |q_{0}|\binom{\tilde{m}+d-2}{d-2}+|q_{1}|\binom{\tilde{m}+d-3}{d-3}+\cdots +|q_{d-2}|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{0}(X,{\mathcal{Q}}_{i}) & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{Q}}_{i}(\tilde{m}))\leqslant \cdots \leqslant h^{0}(X,{\mathcal{Q}}(\tilde{m}))=\unicode[STIX]{x1D712}(X,{\mathcal{Q}}(\tilde{m}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \displaystyle |q_{0}|\binom{\tilde{m}+d-2}{d-2}+|q_{1}|\binom{\tilde{m}+d-3}{d-3}+\cdots +|q_{d-2}|.\nonumber\end{eqnarray}$$
This implies that
![]() $h^{0}(X,{\mathcal{Q}}_{i})\leqslant p^{d-1}P^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1},\tilde{m})$
, where
$h^{0}(X,{\mathcal{Q}}_{i})\leqslant p^{d-1}P^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1},\tilde{m})$
, where
![]() $P^{d}(X_{0},\ldots ,X_{d-1},Y)$
is a universal polynomial function with rational coefficients. Therefore,
$P^{d}(X_{0},\ldots ,X_{d-1},Y)$
is a universal polynomial function with rational coefficients. Therefore,
The inequality for
![]() $D_{0}({\mathcal{Q}})$
follows similarly. This proves the assertion (2) and hence the lemma.◻
$D_{0}({\mathcal{Q}})$
follows similarly. This proves the assertion (2) and hence the lemma.◻
Lemma 2.8. Given
![]() $d\geqslant 2$
, there exist universal polynomials
$d\geqslant 2$
, there exist universal polynomials
![]() $\bar{P}_{2}^{d}$
,
$\bar{P}_{2}^{d}$
,
![]() $\bar{P}_{3}^{d}$
$\bar{P}_{3}^{d}$
![]() $\in \mathbb{Q}[X_{0},\ldots ,X_{d-1},Y]$
such that, if
$\in \mathbb{Q}[X_{0},\ldots ,X_{d-1},Y]$
such that, if
![]() $X$
is an integral projective variety of dimension
$X$
is an integral projective variety of dimension
![]() $d-1\geqslant 1$
with Hilbert polynomial and
$d-1\geqslant 1$
with Hilbert polynomial and
![]() $\bar{m}$
as in Notations 2.2, and if there are short exact sequences of
$\bar{m}$
as in Notations 2.2, and if there are short exact sequences of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
then
where
![]() $m_{0}\geqslant 0$
and
$m_{0}\geqslant 0$
and
![]() $n_{2}\geqslant 0$
are two integers.
$n_{2}\geqslant 0$
are two integers.
Proof. Without loss of generality, one can assume that
![]() $m_{0}\geqslant 1$
and
$m_{0}\geqslant 1$
and
![]() $n_{2}\geqslant 1$
. Since
$n_{2}\geqslant 1$
. Since
![]() ${\mathcal{O}}_{X}$
is
${\mathcal{O}}_{X}$
is
![]() $\bar{m}$
-regular, the sheaf
$\bar{m}$
-regular, the sheaf
![]() ${\mathcal{M}}_{1}$
is an
${\mathcal{M}}_{1}$
is an
![]() $\bar{m}+m_{0}$
-regular sheaf of
$\bar{m}+m_{0}$
-regular sheaf of
![]() ${\mathcal{O}}_{X}$
-modules of dimension
${\mathcal{O}}_{X}$
-modules of dimension
![]() $d-2$
. Therefore, for any
$d-2$
. Therefore, for any
![]() ${\mathcal{M}}_{1}$
-sequence
${\mathcal{M}}_{1}$
-sequence
![]() $a_{1},\ldots ,a_{d-2}$
, the sheaf of
$a_{1},\ldots ,a_{d-2}$
, the sheaf of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
![]() ${\mathcal{M}}_{1i}:={\mathcal{M}}_{1}/(a_{d-2},\ldots ,a_{i+1}){\mathcal{M}}_{1}$
is
${\mathcal{M}}_{1i}:={\mathcal{M}}_{1}/(a_{d-2},\ldots ,a_{i+1}){\mathcal{M}}_{1}$
is
![]() $\bar{m}+m_{0}$
-regular. This implies
$\bar{m}+m_{0}$
-regular. This implies
 $$\begin{eqnarray}\displaystyle h^{0}(X,{\mathcal{M}}_{1i}) & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{M}}_{1i}(\bar{m}+m_{0}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{M}}_{1}(\bar{m}+m_{0}))\leqslant h^{0}(X,{\mathcal{O}}_{X}(\bar{m}+m_{0}))\nonumber\\ \displaystyle & = & \displaystyle \tilde{e}_{0}\binom{\bar{m}+m_{0}+d-1}{d-1}-\tilde{e}_{1}\binom{\bar{m}+m_{0}+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +(-1)^{d-1}\tilde{e}_{d-1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {\tilde{e}_{0}}^{2}\binom{\bar{m}+d+d-1}{d-1}m_{0}^{d-1}+{\tilde{e}_{1}}^{2}\binom{\bar{m}+d+d-2}{d-2}m_{0}^{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +{\tilde{e}_{d-1}}^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {m_{0}}^{d-1}\tilde{P}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1},\bar{m}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{0}(X,{\mathcal{M}}_{1i}) & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{M}}_{1i}(\bar{m}+m_{0}))\nonumber\\ \displaystyle & {\leqslant} & \displaystyle h^{0}(X,{\mathcal{M}}_{1}(\bar{m}+m_{0}))\leqslant h^{0}(X,{\mathcal{O}}_{X}(\bar{m}+m_{0}))\nonumber\\ \displaystyle & = & \displaystyle \tilde{e}_{0}\binom{\bar{m}+m_{0}+d-1}{d-1}-\tilde{e}_{1}\binom{\bar{m}+m_{0}+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +(-1)^{d-1}\tilde{e}_{d-1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {\tilde{e}_{0}}^{2}\binom{\bar{m}+d+d-1}{d-1}m_{0}^{d-1}+{\tilde{e}_{1}}^{2}\binom{\bar{m}+d+d-2}{d-2}m_{0}^{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +{\tilde{e}_{d-1}}^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle {m_{0}}^{d-1}\tilde{P}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1},\bar{m}),\nonumber\end{eqnarray}$$
where the second last inequality follows as
![]() $\tilde{e}_{i}\leqslant {\tilde{e}_{i}}^{2}$
and
$\tilde{e}_{i}\leqslant {\tilde{e}_{i}}^{2}$
and
![]() $\bar{m}+m_{0}+k\leqslant (\bar{m}+d+k)m_{0}$
, for any
$\bar{m}+m_{0}+k\leqslant (\bar{m}+d+k)m_{0}$
, for any
![]() $k\geqslant 0$
, and
$k\geqslant 0$
, and
![]() $\tilde{P}^{d}(X_{0},\ldots ,X_{d-1},Y)$
is a universal polynomial function with rational coefficients.
$\tilde{P}^{d}(X_{0},\ldots ,X_{d-1},Y)$
is a universal polynomial function with rational coefficients.
Let
![]() $e_{i}({\mathcal{M}}_{1})$
denote the
$e_{i}({\mathcal{M}}_{1})$
denote the
![]() $i$
th coefficient of the Hilbert polynomial of
$i$
th coefficient of the Hilbert polynomial of
![]() ${\mathcal{M}}_{1}$
with respect to the line bundle
${\mathcal{M}}_{1}$
with respect to the line bundle
![]() ${\mathcal{O}}_{X}(1)$
. Then, by Lemma A.1, we have
${\mathcal{O}}_{X}(1)$
. Then, by Lemma A.1, we have
![]() $e_{i}({\mathcal{M}}_{1})\leqslant m_{0}^{i+1}P_{i}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{i})$
, where
$e_{i}({\mathcal{M}}_{1})\leqslant m_{0}^{i+1}P_{i}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{i})$
, where
![]() $P_{i}^{d}(X_{0},\ldots ,X_{i})$
is a universal polynomial with rational coefficients.
$P_{i}^{d}(X_{0},\ldots ,X_{i})$
is a universal polynomial with rational coefficients.
Now, the bound for
![]() $2C_{0}({\mathcal{M}}_{1})+D_{0}({\mathcal{M}}_{1})$
follows. The identical proof follows for
$2C_{0}({\mathcal{M}}_{1})+D_{0}({\mathcal{M}}_{1})$
follows. The identical proof follows for
![]() ${\mathcal{M}}_{2}$
.◻
${\mathcal{M}}_{2}$
.◻
Notations 2.9. For a pair
![]() $(R,I)$
, where
$(R,I)$
, where
![]() $R$
is a standard graded ring of
$R$
is a standard graded ring of
![]() $\text{char}~p>0$
and of dimension
$\text{char}~p>0$
and of dimension
![]() $d\geqslant 2$
, and
$d\geqslant 2$
, and
![]() $I\subset R$
is a graded ideal of finite colength, we define (similarly to the sequence of functions that had been defined in [Reference TrivediT4]) a sequence of functions
$I\subset R$
is a graded ideal of finite colength, we define (similarly to the sequence of functions that had been defined in [Reference TrivediT4]) a sequence of functions
![]() $\{f_{n}:[1,\infty )\rightarrow [0,\infty )\}_{n}$
as follows.
$\{f_{n}:[1,\infty )\rightarrow [0,\infty )\}_{n}$
as follows.
Fix
![]() $n\in \mathbb{N}$
and denote
$n\in \mathbb{N}$
and denote
![]() $q=p^{n}$
. Let
$q=p^{n}$
. Let
![]() $x\in [1,\infty )$
; then, there exists a unique nonnegative integer
$x\in [1,\infty )$
; then, there exists a unique nonnegative integer
![]() $m$
such that
$m$
such that
![]() $(m+q)/q\leqslant x<(m+q+1)/q$
. Then,
$(m+q)/q\leqslant x<(m+q+1)/q$
. Then,
Lemma 2.10. Each
![]() $f_{n}:[1,\infty )\longrightarrow [0,\infty )$
, defined as in Notations 2.9, is a compactly supported function such that
$f_{n}:[1,\infty )\longrightarrow [0,\infty )$
, defined as in Notations 2.9, is a compactly supported function such that
![]() $\cup _{n\geqslant 1}\text{Supp}~f_{n}\subseteq [1,n_{0}\unicode[STIX]{x1D707}]$
, where
$\cup _{n\geqslant 1}\text{Supp}~f_{n}\subseteq [1,n_{0}\unicode[STIX]{x1D707}]$
, where
![]() $R_{n_{0}}\subseteq I$
and
$R_{n_{0}}\subseteq I$
and
![]() $\unicode[STIX]{x1D707}\geqslant \unicode[STIX]{x1D707}(I)$
.
$\unicode[STIX]{x1D707}\geqslant \unicode[STIX]{x1D707}(I)$
.
Proof. Since
![]() $R$
is a standard graded ring, for
$R$
is a standard graded ring, for
![]() $m\geqslant n_{0}\unicode[STIX]{x1D707}q$
, we have
$m\geqslant n_{0}\unicode[STIX]{x1D707}q$
, we have
![]() $R_{m}\subseteq (R_{n_{0}})^{\unicode[STIX]{x1D707}q}\subseteq I^{\unicode[STIX]{x1D707}q}\subseteq I^{[q]}$
. This implies that
$R_{m}\subseteq (R_{n_{0}})^{\unicode[STIX]{x1D707}q}\subseteq I^{\unicode[STIX]{x1D707}q}\subseteq I^{[q]}$
. This implies that
![]() $\ell (R/I^{[q]})_{m}=0$
, if
$\ell (R/I^{[q]})_{m}=0$
, if
![]() $m\geqslant n_{0}\unicode[STIX]{x1D707}q$
. Therefore, support
$m\geqslant n_{0}\unicode[STIX]{x1D707}q$
. Therefore, support
![]() $f_{n}\subseteq [1,n_{0}\unicode[STIX]{x1D707}]$
, for every
$f_{n}\subseteq [1,n_{0}\unicode[STIX]{x1D707}]$
, for every
![]() $n\geqslant 0$
. This proves the lemma.◻
$n\geqslant 0$
. This proves the lemma.◻
Proposition 2.11. For
![]() $f_{n}$
as given in Notations 2.9, we have
$f_{n}$
as given in Notations 2.9, we have
(1)
 $|f_{n}(x)-f_{n+1}(x)|\leqslant C/p^{n-d+2}$
, for every
$|f_{n}(x)-f_{n+1}(x)|\leqslant C/p^{n-d+2}$
, for every
 $x\geqslant 1$
and for all
$x\geqslant 1$
and for all
 $n\geqslant 0$
.
$n\geqslant 0$
.(2) In particular,
 $\Vert f_{n}-f_{n+1}\Vert \leqslant C/p^{n-d+2}$
and
$\Vert f_{n}-f_{n+1}\Vert \leqslant C/p^{n-d+2}$
and
 $\Vert f_{d-1}-f_{d}\Vert \leqslant C/p$
, where (8)the integers
$\Vert f_{d-1}-f_{d}\Vert \leqslant C/p$
, where (8)the integers $$\begin{eqnarray}C=2C_{R}+\unicode[STIX]{x1D707}\left(\bar{m}+n_{0}\left(\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D707}}d_{i}\right)+1\right)^{d-2}(\bar{P}_{1}^{d}+d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{3}^{d}),\end{eqnarray}$$
$$\begin{eqnarray}C=2C_{R}+\unicode[STIX]{x1D707}\left(\bar{m}+n_{0}\left(\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D707}}d_{i}\right)+1\right)^{d-2}(\bar{P}_{1}^{d}+d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{3}^{d}),\end{eqnarray}$$
 $\bar{m}$
and
$\bar{m}$
and
 $n_{0}$
are given as in Notations 2.2, and
$n_{0}$
are given as in Notations 2.2, and
 $d_{1},\ldots ,d_{\unicode[STIX]{x1D707}}$
are degrees of a chosen generator of
$d_{1},\ldots ,d_{\unicode[STIX]{x1D707}}$
are degrees of a chosen generator of
 $I$
. Moreover,
$I$
. Moreover,
 $C_{R}=\unicode[STIX]{x1D707}h^{0}(X,{\mathcal{O}}_{X}(\bar{m}))$
, for
$C_{R}=\unicode[STIX]{x1D707}h^{0}(X,{\mathcal{O}}_{X}(\bar{m}))$
, for
 $X=\text{Proj}~R$
, and
$X=\text{Proj}~R$
, and
 $\bar{P}_{1}^{d}$
,
$\bar{P}_{1}^{d}$
,
 $\bar{P}_{2}^{d}$
, and
$\bar{P}_{2}^{d}$
, and
 $\bar{P}_{3}^{d}$
are given as in Lemmas 2.7 and 2.8.
$\bar{P}_{3}^{d}$
are given as in Lemmas 2.7 and 2.8.
Proof. Fix
![]() $x\in [1,\infty )$
. Therefore, for given
$x\in [1,\infty )$
. Therefore, for given
![]() $q=p^{n}$
, there exists a unique integer
$q=p^{n}$
, there exists a unique integer
![]() $m\geqslant 0$
, such that
$m\geqslant 0$
, such that
![]() $(m+q)/q\leqslant x<(m+q+1)/q$
and
$(m+q)/q\leqslant x<(m+q+1)/q$
and
Hence,
and
Now, by Equation (4) in Remark 2.3, we have
Consider the short exact sequence of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
Then, for any locally free sheaf
![]() $P$
of
$P$
of
![]() ${\mathcal{O}}_{X}$
-modules and for
${\mathcal{O}}_{X}$
-modules and for
![]() $m\geqslant 0$
, we have the following short exact sequence of
$m\geqslant 0$
, we have the following short exact sequence of
![]() ${\mathcal{O}}_{X}$
-modules:
${\mathcal{O}}_{X}$
-modules:
Since
 $$\begin{eqnarray}\displaystyle \text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X}) & = & \displaystyle h^{0}(X,{\mathcal{O}}_{X}(m+q))-\mathop{\sum }_{i}h^{0}(X,{\mathcal{O}}_{X}(m+q-qd_{i}))\nonumber\\ \displaystyle & & \displaystyle +\,h^{0}(X,(F^{n\ast }V)(m)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X}) & = & \displaystyle h^{0}(X,{\mathcal{O}}_{X}(m+q))-\mathop{\sum }_{i}h^{0}(X,{\mathcal{O}}_{X}(m+q-qd_{i}))\nonumber\\ \displaystyle & & \displaystyle +\,h^{0}(X,(F^{n\ast }V)(m)),\nonumber\end{eqnarray}$$
we have (by taking
![]() $P=V~\text{and}=\sum \,{\mathcal{O}}_{X}(1-d_{i})$
, respectively)
$P=V~\text{and}=\sum \,{\mathcal{O}}_{X}(1-d_{i})$
, respectively)
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{m-d,q}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant |h^{0}(X,{\mathcal{O}}_{X}(m+q))-h^{0}(X,{\mathcal{O}}_{X}(m-d+q))|\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{i}|h^{0}(X,{\mathcal{O}}_{X}(m+q-qd_{i}))\nonumber\\ \displaystyle & & \displaystyle \qquad -\,h^{0}(X,{\mathcal{O}}_{X}(m-d+q-qd_{i}))|+|h^{0}(X,(F^{n\ast }V)(m))\nonumber\\ \displaystyle & & \displaystyle \qquad -\,h^{0}(X,(F^{n\ast }V)(m-d))|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant h^{0}(X,{\mathcal{M}}_{1}(m+q))+h^{0}\left(X,\mathop{\sum }_{i}{\mathcal{O}}_{X}(q-qd_{i})\otimes {\mathcal{M}}_{1}(m)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,h^{0}(X,F^{n\ast }V\otimes {\mathcal{M}}_{1}(m)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{m-d,q}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant |h^{0}(X,{\mathcal{O}}_{X}(m+q))-h^{0}(X,{\mathcal{O}}_{X}(m-d+q))|\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\mathop{\sum }_{i}|h^{0}(X,{\mathcal{O}}_{X}(m+q-qd_{i}))\nonumber\\ \displaystyle & & \displaystyle \qquad -\,h^{0}(X,{\mathcal{O}}_{X}(m-d+q-qd_{i}))|+|h^{0}(X,(F^{n\ast }V)(m))\nonumber\\ \displaystyle & & \displaystyle \qquad -\,h^{0}(X,(F^{n\ast }V)(m-d))|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant h^{0}(X,{\mathcal{M}}_{1}(m+q))+h^{0}\left(X,\mathop{\sum }_{i}{\mathcal{O}}_{X}(q-qd_{i})\otimes {\mathcal{M}}_{1}(m)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,h^{0}(X,F^{n\ast }V\otimes {\mathcal{M}}_{1}(m)).\nonumber\end{eqnarray}$$
Let
![]() $d-2=0$
. Then,
$d-2=0$
. Then,
![]() ${\mathcal{M}}_{1}$
is a zero-dimensional sheaf, which implies that
${\mathcal{M}}_{1}$
is a zero-dimensional sheaf, which implies that
![]() $h^{0}(X,{\mathcal{M}}_{1}(m))=h^{0}(X,{\mathcal{M}}_{1})$
, for every
$h^{0}(X,{\mathcal{M}}_{1}(m))=h^{0}(X,{\mathcal{M}}_{1})$
, for every
![]() $m\in \mathbb{Z}$
. Moreover, if
$m\in \mathbb{Z}$
. Moreover, if
![]() $P$
is a locally free sheaf of
$P$
is a locally free sheaf of
![]() ${\mathcal{O}}_{X}$
-modules, then
${\mathcal{O}}_{X}$
-modules, then
![]() $h^{0}(X,P\otimes {\mathcal{M}}_{1})=(\text{rank}~P)h^{0}(X,{\mathcal{M}}_{1})$
. Therefore, we get
$h^{0}(X,P\otimes {\mathcal{M}}_{1})=(\text{rank}~P)h^{0}(X,{\mathcal{M}}_{1})$
. Therefore, we get
If
![]() $d-2>0$
then, by Lemma 2.5,
$d-2>0$
then, by Lemma 2.5,
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{m-d,q}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant D_{0}({\mathcal{M}}_{1})(m+q)^{d-2}+2(\unicode[STIX]{x1D707})C_{0}({\mathcal{M}}_{1})(m^{d-2}+1)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (\unicode[STIX]{x1D707})[2C_{0}({\mathcal{M}}_{1})+D_{0}({\mathcal{M}}_{1})](m+q)^{d-2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{m-d,q}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant D_{0}({\mathcal{M}}_{1})(m+q)^{d-2}+2(\unicode[STIX]{x1D707})C_{0}({\mathcal{M}}_{1})(m^{d-2}+1)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (\unicode[STIX]{x1D707})[2C_{0}({\mathcal{M}}_{1})+D_{0}({\mathcal{M}}_{1})](m+q)^{d-2}.\nonumber\end{eqnarray}$$
Therefore, for
![]() $d-1\geqslant 1$
, we have
$d-1\geqslant 1$
, we have
Since, for a locally free sheaf
![]() $P$
, we have
$P$
, we have
the short exact sequence
as given in the statement of Lemma 2.7, gives a canonical long exact sequence
which implies (by taking
![]() $P=V$
and
$P=V$
and
![]() $V=\sum \,{\mathcal{O}}_{X}(1-d_{i})$
, respectively)
$V=\sum \,{\mathcal{O}}_{X}(1-d_{i})$
, respectively)
 $$\begin{eqnarray}\displaystyle \text{coker}~\unicode[STIX]{x1D719}_{mp,qp}({\mathcal{O}}_{X}) & = & \displaystyle h^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(m+q))\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{i}h^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(q-qd_{i}+m))\nonumber\\ \displaystyle & & \displaystyle +\,h^{0}(X,F^{n\ast }V\otimes (F_{\ast }{\mathcal{O}}_{X})(m+q)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{coker}~\unicode[STIX]{x1D719}_{mp,qp}({\mathcal{O}}_{X}) & = & \displaystyle h^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(m+q))\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{i}h^{0}(X,(F_{\ast }{\mathcal{O}}_{X})(q-qd_{i}+m))\nonumber\\ \displaystyle & & \displaystyle +\,h^{0}(X,F^{n\ast }V\otimes (F_{\ast }{\mathcal{O}}_{X})(m+q)).\nonumber\end{eqnarray}$$
Therefore, we have
The short exact sequence of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
gives
which gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \!\!|\text{coker}~\unicode[STIX]{x1D719}_{mp,qp}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & & \displaystyle \!\!\quad \leqslant \left[h^{0}(X,F^{(n+1)\ast }V\otimes {\mathcal{M}}_{2}(mp))+h^{0}\!\left(\!X,\mathop{\sum }_{i}{\mathcal{O}}_{X}(qp-qpd_{i})\otimes {\mathcal{M}}_{2}(mp)\!\right)\right.\nonumber\\ \displaystyle & & \displaystyle \!\!\qquad +\left.h^{0}(X,{\mathcal{M}}_{2}(mp+qp))\vphantom{\left(\mathop{\sum }_{i}\right)}\right]\leqslant 2(\unicode[STIX]{x1D707})C_{0}({\mathcal{M}}_{2})((mp)^{d-2}+1)\nonumber\\ \displaystyle & & \displaystyle \!\!\qquad +\,(\unicode[STIX]{x1D707})D_{0}({\mathcal{M}}_{2})(mp+qp)^{d-2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \!\!|\text{coker}~\unicode[STIX]{x1D719}_{mp,qp}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & & \displaystyle \!\!\quad \leqslant \left[h^{0}(X,F^{(n+1)\ast }V\otimes {\mathcal{M}}_{2}(mp))+h^{0}\!\left(\!X,\mathop{\sum }_{i}{\mathcal{O}}_{X}(qp-qpd_{i})\otimes {\mathcal{M}}_{2}(mp)\!\right)\right.\nonumber\\ \displaystyle & & \displaystyle \!\!\qquad +\left.h^{0}(X,{\mathcal{M}}_{2}(mp+qp))\vphantom{\left(\mathop{\sum }_{i}\right)}\right]\leqslant 2(\unicode[STIX]{x1D707})C_{0}({\mathcal{M}}_{2})((mp)^{d-2}+1)\nonumber\\ \displaystyle & & \displaystyle \!\!\qquad +\,(\unicode[STIX]{x1D707})D_{0}({\mathcal{M}}_{2})(mp+qp)^{d-2}.\nonumber\end{eqnarray}$$
Therefore,
Combining Equations (10)–(12), we get
 $$\begin{eqnarray}\displaystyle (A) & := & \displaystyle |p^{d-1}\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (\unicode[STIX]{x1D707})[2C_{0}({\mathcal{M}}_{1})+D_{0}({\mathcal{M}}_{1})](m+q)^{d-2}p^{d-1}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D707})[2C_{0}({\mathcal{Q}})+D_{0}({\mathcal{Q}})](m+q)^{d-2}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D707})[2C_{0}({\mathcal{M}}_{2})+D_{0}({\mathcal{M}}_{2})](mp+qp)^{d-2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (A) & := & \displaystyle |p^{d-1}\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})-\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle (\unicode[STIX]{x1D707})[2C_{0}({\mathcal{M}}_{1})+D_{0}({\mathcal{M}}_{1})](m+q)^{d-2}p^{d-1}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D707})[2C_{0}({\mathcal{Q}})+D_{0}({\mathcal{Q}})](m+q)^{d-2}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D707})[2C_{0}({\mathcal{M}}_{2})+D_{0}({\mathcal{M}}_{2})](mp+qp)^{d-2}.\nonumber\end{eqnarray}$$
Therefore,
Now, if we denote
![]() $\bar{P}_{i}^{d}=\bar{P}_{i}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1},\tilde{m})$
, for
$\bar{P}_{i}^{d}=\bar{P}_{i}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1},\tilde{m})$
, for
![]() $i=1,2$
, and 3, then, by Lemma 2.7,
$i=1,2$
, and 3, then, by Lemma 2.7,
and, by Lemma 2.8, we have
and
where the last inequality follows as
![]() $n_{2}<p$
. Therefore, we have
$n_{2}<p$
. Therefore, we have
Now, multiplying the above inequality by
![]() $1/(qp)^{d-1}$
, we get
$1/(qp)^{d-1}$
, we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left|\frac{\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})}{q^{d-1}}-\frac{\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})}{(qp)^{d-1}}\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (\unicode[STIX]{x1D707})\frac{(m+q)^{d-2}}{q^{d-1}}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+p^{d-2}\bar{P}_{3}^{d}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left|\frac{\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})}{q^{d-1}}-\frac{\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})}{(qp)^{d-1}}\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (\unicode[STIX]{x1D707})\frac{(m+q)^{d-2}}{q^{d-1}}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+p^{d-2}\bar{P}_{3}^{d}].\nonumber\end{eqnarray}$$
Moreover, by Remark 2.3,
 $$\begin{eqnarray}\displaystyle m+q & {\geqslant} & \displaystyle \bar{m}+n_{0}\left(\mathop{\sum }_{i}d_{i}\right)q+q\Rightarrow \text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})\nonumber\\ \displaystyle & = & \displaystyle \text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m+q & {\geqslant} & \displaystyle \bar{m}+n_{0}\left(\mathop{\sum }_{i}d_{i}\right)q+q\Rightarrow \text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})\nonumber\\ \displaystyle & = & \displaystyle \text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})=0.\nonumber\end{eqnarray}$$
Furthermore,
![]() $m+q\leqslant \bar{m}+n_{0}(\sum _{i}d_{i})q+q,\Rightarrow (m+q)^{d-2}\leqslant L_{0}q^{d-2}$
, where
$m+q\leqslant \bar{m}+n_{0}(\sum _{i}d_{i})q+q,\Rightarrow (m+q)^{d-2}\leqslant L_{0}q^{d-2}$
, where
Therefore, for every
![]() $m\geqslant 0$
and
$m\geqslant 0$
and
![]() $n\geqslant 1$
, where
$n\geqslant 1$
, where
![]() $q=p^{n}$
, we have
$q=p^{n}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})/q^{d-1}-\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})/(qp)^{d-1}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant ((\unicode[STIX]{x1D707})L_{0}q^{d-2}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+p^{d-2}\bar{P}_{3}^{d}])/q^{d-1}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant ((\unicode[STIX]{x1D707})L_{0}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+\bar{P}_{3}^{d}]p^{d-2}q^{d-2})/q^{d-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\text{coker}~\unicode[STIX]{x1D719}_{m,q}({\mathcal{O}}_{X})/q^{d-1}-\text{coker}~\unicode[STIX]{x1D719}_{mp+n_{2},qp}({\mathcal{O}}_{X})/(qp)^{d-1}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant ((\unicode[STIX]{x1D707})L_{0}q^{d-2}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+p^{d-2}\bar{P}_{3}^{d}])/q^{d-1}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant ((\unicode[STIX]{x1D707})L_{0}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+\bar{P}_{3}^{d}]p^{d-2}q^{d-2})/q^{d-1}.\nonumber\end{eqnarray}$$
Now, by Equation (9), we have
 $$\begin{eqnarray}\displaystyle |f_{n}(x)-f_{n+1}(x)| & {\leqslant} & \displaystyle \frac{C_{R}}{q^{d-1}}+\frac{C_{R}}{(qp)^{d-1}}+(\unicode[STIX]{x1D707})L_{0}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+\bar{P}_{3}^{d}]\frac{p^{d-2}}{q}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\frac{p^{d-2}}{q},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |f_{n}(x)-f_{n+1}(x)| & {\leqslant} & \displaystyle \frac{C_{R}}{q^{d-1}}+\frac{C_{R}}{(qp)^{d-1}}+(\unicode[STIX]{x1D707})L_{0}[d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+\bar{P}_{3}^{d}]\frac{p^{d-2}}{q}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\frac{p^{d-2}}{q},\nonumber\end{eqnarray}$$
where
![]() $C=2C_{R}+(\unicode[STIX]{x1D707})L_{0}(d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+\bar{P}_{3}^{d})$
, which proves the proposition. ◻
$C=2C_{R}+(\unicode[STIX]{x1D707})L_{0}(d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{1}^{d}+\bar{P}_{3}^{d})$
, which proves the proposition. ◻
Corollary 2.12. There exists a constant
![]() $C_{1}=P_{4}^{d}(\tilde{e}_{0},\tilde{e}_{1},\ldots ,\tilde{e}_{d},\bar{m})+(n_{0}\unicode[STIX]{x1D707}-1)C$
, where
$C_{1}=P_{4}^{d}(\tilde{e}_{0},\tilde{e}_{1},\ldots ,\tilde{e}_{d},\bar{m})+(n_{0}\unicode[STIX]{x1D707}-1)C$
, where
![]() $C$
is as in Proposition 2.11, and
$C$
is as in Proposition 2.11, and
![]() $P_{4}^{d}(X_{0},\ldots ,X_{d},Y)$
is a universal polynomial function with rational coefficients such that, for
$P_{4}^{d}(X_{0},\ldots ,X_{d},Y)$
is a universal polynomial function with rational coefficients such that, for
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
Proof. Note that
where the last equality follows from Lemma 2.10. Hence,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left|\frac{1}{(p^{n})^{d}}\ell \left(\frac{R}{I^{[p^{n}]}}\right)-\frac{1}{(p^{n+1})^{d}}\ell \left(\frac{R}{I^{[p^{n+1}]}}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left|\frac{1}{p^{nd}}\ell \left(\frac{R}{\mathbf{m}^{p^{n}}}\right)-\frac{1}{p^{(n+1)d}}\ell \left(\frac{R}{\mathbf{m}^{p^{n+1}}}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \qquad +\left|\int _{1}^{n_{0}\unicode[STIX]{x1D707}}f_{n}(x)\,dx-\int _{1}^{n_{0}\unicode[STIX]{x1D707}}f_{n+1}(x)\,dx\right|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left|\frac{1}{(p^{n})^{d}}\ell \left(\frac{R}{I^{[p^{n}]}}\right)-\frac{1}{(p^{n+1})^{d}}\ell \left(\frac{R}{I^{[p^{n+1}]}}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left|\frac{1}{p^{nd}}\ell \left(\frac{R}{\mathbf{m}^{p^{n}}}\right)-\frac{1}{p^{(n+1)d}}\ell \left(\frac{R}{\mathbf{m}^{p^{n+1}}}\right)\right|\nonumber\\ \displaystyle & & \displaystyle \qquad +\left|\int _{1}^{n_{0}\unicode[STIX]{x1D707}}f_{n}(x)\,dx-\int _{1}^{n_{0}\unicode[STIX]{x1D707}}f_{n+1}(x)\,dx\right|.\nonumber\end{eqnarray}$$
If
![]() $p^{n}\leqslant \bar{m}$
, then
$p^{n}\leqslant \bar{m}$
, then
 $$\begin{eqnarray}\displaystyle \left|\frac{1}{p^{nd}}\ell \left(\frac{R}{\mathbf{m}^{p^{n}}}\right)-\frac{1}{p^{(n+1)d}}\ell \left(\frac{R}{\mathbf{m}^{p^{n+1}}}\right)\right| & {\leqslant} & \displaystyle \left|\frac{P_{(R,\mathbf{m})}(\bar{m})}{p^{nd}}+\frac{P_{(R,\mathbf{m})}(\bar{m}^{2})}{p^{(n+1)d}}\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{P_{(R,\mathbf{m})}(\bar{m}^{2})}{p^{n}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left|\frac{1}{p^{nd}}\ell \left(\frac{R}{\mathbf{m}^{p^{n}}}\right)-\frac{1}{p^{(n+1)d}}\ell \left(\frac{R}{\mathbf{m}^{p^{n+1}}}\right)\right| & {\leqslant} & \displaystyle \left|\frac{P_{(R,\mathbf{m})}(\bar{m})}{p^{nd}}+\frac{P_{(R,\mathbf{m})}(\bar{m}^{2})}{p^{(n+1)d}}\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{P_{(R,\mathbf{m})}(\bar{m}^{2})}{p^{n}},\nonumber\end{eqnarray}$$
where
![]() $P_{(R,\mathbf{m})}$
is the Hilbert polynomial of
$P_{(R,\mathbf{m})}$
is the Hilbert polynomial of
![]() $R$
with respect to
$R$
with respect to
![]() $\mathbf{m}$
. If
$\mathbf{m}$
. If
![]() $p^{n}>\bar{m}$
, then there exists a universal polynomial function
$p^{n}>\bar{m}$
, then there exists a universal polynomial function
![]() $P_{6}^{d}(X_{0},\ldots ,X_{d})$
with rational coefficients such that
$P_{6}^{d}(X_{0},\ldots ,X_{d})$
with rational coefficients such that
Therefore, combining this with Proposition 2.11, part (1), we get a universal polynomial function
![]() $P_{4}^{d}(X_{0},\ldots ,X_{d},Y)$
with rational coefficients such that
$P_{4}^{d}(X_{0},\ldots ,X_{d},Y)$
with rational coefficients such that
Since
![]() $d\geqslant 2$
, the corollary follows.◻
$d\geqslant 2$
, the corollary follows.◻
3 Hilbert–Kunz density function and reduction mod
 $p$
$p$
Remark 3.1. Let
![]() $R$
be a standard graded integral domain of dimension
$R$
be a standard graded integral domain of dimension
![]() $d\geqslant 2$
, with
$d\geqslant 2$
, with
![]() $R_{0}=k$
, where
$R_{0}=k$
, where
![]() $k$
is an algebraically closed field. Let
$k$
is an algebraically closed field. Let
![]() $N=\ell (R_{1})-1$
; then, we have a surjective graded map
$N=\ell (R_{1})-1$
; then, we have a surjective graded map
![]() $k[X_{0},\ldots ,X_{N}]\longrightarrow R$
of degree 0, given by
$k[X_{0},\ldots ,X_{N}]\longrightarrow R$
of degree 0, given by
![]() $X_{i}$
mapping to generators of
$X_{i}$
mapping to generators of
![]() $R_{1}$
. This gives a closed immersion
$R_{1}$
. This gives a closed immersion
![]() $X=\text{Proj}~R\longrightarrow \mathbb{P}_{k}^{N}$
such that
$X=\text{Proj}~R\longrightarrow \mathbb{P}_{k}^{N}$
such that
![]() ${\mathcal{O}}_{X}(1)={\mathcal{O}}_{\mathbb{P}_{k}^{N}}(1)\mid _{X}$
. Therefore, if
${\mathcal{O}}_{X}(1)={\mathcal{O}}_{\mathbb{P}_{k}^{N}}(1)\mid _{X}$
. Therefore, if
is the Hilbert–Samuel polynomial of
![]() $R$
, with respect to
$R$
, with respect to
![]() $\mathbf{m}$
, then, the Hilbert polynomial for the pair
$\mathbf{m}$
, then, the Hilbert polynomial for the pair
![]() $(X,{\mathcal{O}}_{X}(1))$
is
$(X,{\mathcal{O}}_{X}(1))$
is
Since
![]() $R$
is a domain, the canonical graded map
$R$
is a domain, the canonical graded map
![]() $R=\oplus _{m}{R_{m}\longrightarrow \oplus }_{m}H^{0}(X,{\mathcal{O}}_{X}(m))$
is injective.
$R=\oplus _{m}{R_{m}\longrightarrow \oplus }_{m}H^{0}(X,{\mathcal{O}}_{X}(m))$
is injective.
Let
![]() ${\mathcal{I}}_{X}$
be the ideal sheaf of
${\mathcal{I}}_{X}$
be the ideal sheaf of
![]() $X$
in
$X$
in
![]() $\mathbb{P}_{k}^{N}$
; then, we have the canonical short exact sequence of
$\mathbb{P}_{k}^{N}$
; then, we have the canonical short exact sequence of
![]() ${\mathcal{O}}_{\mathbb{P}_{k}^{N}}$
-modules
${\mathcal{O}}_{\mathbb{P}_{k}^{N}}$
-modules
and the image of the induced map
![]() $f_{m}:H^{0}(\mathbb{P}_{k}^{N},{\mathcal{O}}_{\mathbb{P}_{k}^{N}}(m))\longrightarrow H^{0}(X,{\mathcal{O}}_{X}(m))$
is
$f_{m}:H^{0}(\mathbb{P}_{k}^{N},{\mathcal{O}}_{\mathbb{P}_{k}^{N}}(m))\longrightarrow H^{0}(X,{\mathcal{O}}_{X}(m))$
is
![]() $R_{m}$
. Now, by Exp XIII, (6.2) (in [Reference Grothendieck, Berthellot and IllusieSGA 6]), there exists a universal polynomial
$R_{m}$
. Now, by Exp XIII, (6.2) (in [Reference Grothendieck, Berthellot and IllusieSGA 6]), there exists a universal polynomial
![]() $P_{5}^{d}(t_{0},\ldots ,t_{d-1})$
with rational coefficients such that the sheaf
$P_{5}^{d}(t_{0},\ldots ,t_{d-1})$
with rational coefficients such that the sheaf
![]() ${\mathcal{I}}_{X}$
is
${\mathcal{I}}_{X}$
is
![]() $\bar{m}=P_{5}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1})$
-regular. Therefore, the map
$\bar{m}=P_{5}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1})$
-regular. Therefore, the map
![]() $f_{m}$
is surjective for
$f_{m}$
is surjective for
![]() $m\geqslant \bar{m}$
.
$m\geqslant \bar{m}$
.
In particular, we have
(1)
 $R_{m}=H^{0}(X,{\mathcal{O}}_{X}(m))$
, for all
$R_{m}=H^{0}(X,{\mathcal{O}}_{X}(m))$
, for all
 $m\geqslant \bar{m}$
, and
$m\geqslant \bar{m}$
, and(2) the sheaf
 ${\mathcal{O}}_{X}$
is
${\mathcal{O}}_{X}$
is
 $\bar{m}$
-regular with respect to
$\bar{m}$
-regular with respect to
 ${\mathcal{O}}_{X}(1)$
.
${\mathcal{O}}_{X}(1)$
.
Next, we recall a notion of spread.
Definition 3.2. Consider the pair
![]() $(R,I)$
, where
$(R,I)$
, where
![]() $R$
is a finitely generated
$R$
is a finitely generated
![]() $\mathbb{Z}_{{\geqslant}0}$
-graded
$\mathbb{Z}_{{\geqslant}0}$
-graded
![]() $d$
-dimensional domain such that
$d$
-dimensional domain such that
![]() $R_{0}$
is an algebraically closed field
$R_{0}$
is an algebraically closed field
![]() $k$
of characteristic 0, and
$k$
of characteristic 0, and
![]() $I\subset R$
is a homogeneous ideal of finite colength. For such a pair, there exist a finitely generated
$I\subset R$
is a homogeneous ideal of finite colength. For such a pair, there exist a finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A\subseteq k$
, a finitely generated
$A\subseteq k$
, a finitely generated
![]() $\mathbb{N}$
-graded algebra
$\mathbb{N}$
-graded algebra
![]() $R_{A}$
over
$R_{A}$
over
![]() $A$
, and a homogeneous ideal
$A$
, and a homogeneous ideal
![]() $I_{A}\subset R_{A}$
such that
$I_{A}\subset R_{A}$
such that
![]() $R_{A}\otimes _{A}k=R$
and
$R_{A}\otimes _{A}k=R$
and
![]() $I=\text{Im}(I_{A}\otimes _{A}k)$
. We call
$I=\text{Im}(I_{A}\otimes _{A}k)$
. We call
![]() $(A,R_{A},I_{A})$
a spread of the pair
$(A,R_{A},I_{A})$
a spread of the pair
![]() $(R,I)$
.
$(R,I)$
.
Moreover, if, for the pair
![]() $(R,I)$
, we have a spread
$(R,I)$
, we have a spread
![]() $(A,R_{A},I_{A})$
as above and
$(A,R_{A},I_{A})$
as above and
![]() $A\subset A^{\prime }\subset k$
, for some finitely generated
$A\subset A^{\prime }\subset k$
, for some finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A^{\prime }$
, then
$A^{\prime }$
, then
![]() $(A^{\prime },R_{A^{\prime }},I_{A^{\prime }})$
satisfy the same properties as
$(A^{\prime },R_{A^{\prime }},I_{A^{\prime }})$
satisfy the same properties as
![]() $(A,R_{A},I_{A})$
. Hence, we may always assume that the spread
$(A,R_{A},I_{A})$
. Hence, we may always assume that the spread
![]() $(A,R_{A},I_{A})$
as above is chosen such that
$(A,R_{A},I_{A})$
as above is chosen such that
![]() $A$
contains a given finitely generated
$A$
contains a given finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A_{0}\subseteq k$
.
$A_{0}\subseteq k$
.
Notations 3.3. Given a spread
![]() $(A,R_{A},I_{A})$
as above, for a closed point
$(A,R_{A},I_{A})$
as above, for a closed point
![]() $s\in \text{Spec}(A)$
, we define
$s\in \text{Spec}(A)$
, we define
![]() $R_{s}=R_{A}\otimes _{A}\bar{k}(s)$
and the ideal
$R_{s}=R_{A}\otimes _{A}\bar{k}(s)$
and the ideal
![]() $I_{s}=\text{Im}(I_{A}\otimes _{A}\bar{k}(s))\subset R_{s}$
. Similarly, for
$I_{s}=\text{Im}(I_{A}\otimes _{A}\bar{k}(s))\subset R_{s}$
. Similarly, for
![]() $X_{A}:=\text{Proj}~R_{A}$
, we define
$X_{A}:=\text{Proj}~R_{A}$
, we define
![]() $X_{s}:=X\otimes \bar{k}(s)=\text{Proj}~R_{s}$
, and, for a coherent sheaf
$X_{s}:=X\otimes \bar{k}(s)=\text{Proj}~R_{s}$
, and, for a coherent sheaf
![]() $V_{A}$
on
$V_{A}$
on
![]() $X_{A}$
, we define
$X_{A}$
, we define
![]() $V_{s}=V_{A}\otimes \bar{k}(s)$
.
$V_{s}=V_{A}\otimes \bar{k}(s)$
.
Remark 3.4. Note that for a spread
![]() $(A,R_{A},I_{A})$
of
$(A,R_{A},I_{A})$
of
![]() $(R,I)$
as above, the induced map
$(R,I)$
as above, the induced map
![]() $\tilde{\unicode[STIX]{x1D70B}}:X_{A}:=\text{Proj}~R_{A}\longrightarrow \text{Spec}(A)$
is a proper map; hence, by generic flatness, there is an open set (in fact nonempty as
$\tilde{\unicode[STIX]{x1D70B}}:X_{A}:=\text{Proj}~R_{A}\longrightarrow \text{Spec}(A)$
is a proper map; hence, by generic flatness, there is an open set (in fact nonempty as
![]() $A$
is an integral domain)
$A$
is an integral domain)
![]() $U\subset \text{Spec}(A)$
such that
$U\subset \text{Spec}(A)$
such that
![]() $\tilde{\unicode[STIX]{x1D70B}}\mid _{\tilde{\unicode[STIX]{x1D70B}}^{-1}(U)}:\tilde{\unicode[STIX]{x1D70B}}^{-1}(U)\longrightarrow U$
is a proper flat map. Therefore (see [Reference Grothendieck and DieudonnéEGA IV, 12.2.1]), the set
$\tilde{\unicode[STIX]{x1D70B}}\mid _{\tilde{\unicode[STIX]{x1D70B}}^{-1}(U)}:\tilde{\unicode[STIX]{x1D70B}}^{-1}(U)\longrightarrow U$
is a proper flat map. Therefore (see [Reference Grothendieck and DieudonnéEGA IV, 12.2.1]), the set
is a nonempty open set of
![]() $\text{Spec}(A)$
. Hence, by replacing
$\text{Spec}(A)$
. Hence, by replacing
![]() $A$
by a finitely generated
$A$
by a finitely generated
![]() $\mathbb{Z}$
-algebra
$\mathbb{Z}$
-algebra
![]() $A^{\prime }$
such that
$A^{\prime }$
such that
![]() $A\subset A^{\prime }\subset k$
(if necessary), we can assume that
$A\subset A^{\prime }\subset k$
(if necessary), we can assume that
![]() $\tilde{\unicode[STIX]{x1D70B}}$
is a flat map such that for every
$\tilde{\unicode[STIX]{x1D70B}}$
is a flat map such that for every
![]() $s\in \text{Spec}(A)$
, the fiber over
$s\in \text{Spec}(A)$
, the fiber over
![]() $s$
is geometrically integral.
$s$
is geometrically integral.
Therefore, for any closed point
![]() $s\in \text{Spec}(A)$
(i.e., a maximal ideal of
$s\in \text{Spec}(A)$
(i.e., a maximal ideal of
![]() $A$
), the ring
$A$
), the ring
![]() $R_{s}$
is a standard graded
$R_{s}$
is a standard graded
![]() $d$
-dimensional ring such that the ideal
$d$
-dimensional ring such that the ideal
![]() $I_{s}\subset R_{s}$
is a homogeneous ideal of finite colength. Moreover,
$I_{s}\subset R_{s}$
is a homogeneous ideal of finite colength. Moreover,
![]() $X_{s}$
is an integral scheme over
$X_{s}$
is an integral scheme over
![]() $\bar{k}(s)$
.
$\bar{k}(s)$
.
Proof of Theorem 1.1.
For given
![]() $(R,I)$
, and a given spread
$(R,I)$
, and a given spread
![]() $(A,R_{A},I_{A})$
, we can choose a spread
$(A,R_{A},I_{A})$
, we can choose a spread
![]() $(A^{\prime },R_{A^{\prime }},I_{A^{\prime }})$
, where
$(A^{\prime },R_{A^{\prime }},I_{A^{\prime }})$
, where
![]() $A\subset A^{\prime }$
, such that the induced projective morphism of Noetherian schemes
$A\subset A^{\prime }$
, such that the induced projective morphism of Noetherian schemes
![]() $\tilde{\unicode[STIX]{x1D70B}}:X_{A^{\prime }}\longrightarrow A^{\prime }$
is flat, and, for every
$\tilde{\unicode[STIX]{x1D70B}}:X_{A^{\prime }}\longrightarrow A^{\prime }$
is flat, and, for every
![]() $s\in \text{Spec}(A^{\prime })$
, the scheme
$s\in \text{Spec}(A^{\prime })$
, the scheme
![]() $X_{s}$
is an integral scheme over
$X_{s}$
is an integral scheme over
![]() $\bar{k}(s)$
of dimension
$\bar{k}(s)$
of dimension
![]() $=d-1$
. Let
$=d-1$
. Let
![]() $R_{A^{\prime }}=\oplus _{i\geqslant 0}(R_{A^{\prime }})_{i}$
, and let
$R_{A^{\prime }}=\oplus _{i\geqslant 0}(R_{A^{\prime }})_{i}$
, and let
![]() $(R_{A^{\prime }})_{1}$
be generated by
$(R_{A^{\prime }})_{1}$
be generated by
![]() $N$
elements as an
$N$
elements as an
![]() $A^{\prime }$
-module. Then, the canonical graded surjective map
$A^{\prime }$
-module. Then, the canonical graded surjective map
gives a closed immersion
![]() $X_{A^{\prime }}=\text{Proj}~R_{A^{\prime }}\longrightarrow \mathbb{P}_{A^{\prime }}^{N}$
such that
$X_{A^{\prime }}=\text{Proj}~R_{A^{\prime }}\longrightarrow \mathbb{P}_{A^{\prime }}^{N}$
such that
![]() ${\mathcal{O}}_{X_{A^{\prime }}}(1)={\mathcal{O}}_{\mathbb{P}_{A^{\prime }}^{N}}(1)\mid _{X_{A^{\prime }}}$
. Let
${\mathcal{O}}_{X_{A^{\prime }}}(1)={\mathcal{O}}_{\mathbb{P}_{A^{\prime }}^{N}}(1)\mid _{X_{A^{\prime }}}$
. Let
![]() $X_{s}=X_{A^{\prime }}\otimes \bar{k}(s)$
. Then,
$X_{s}=X_{A^{\prime }}\otimes \bar{k}(s)$
. Then,
![]() $X_{s}=\text{Proj}~R_{s}$
, and
$X_{s}=\text{Proj}~R_{s}$
, and
![]() ${\mathcal{O}}_{X_{s}}(1)$
is the canonical line bundle induced by
${\mathcal{O}}_{X_{s}}(1)$
is the canonical line bundle induced by
![]() ${\mathcal{O}}_{X_{A^{\prime }}}(1)$
. Let
${\mathcal{O}}_{X_{A^{\prime }}}(1)$
. Let
![]() $s_{0}=\text{Spec}Q(A)=\text{Spec}Q(A^{\prime })$
be the generic point of
$s_{0}=\text{Spec}Q(A)=\text{Spec}Q(A^{\prime })$
be the generic point of
![]() $\text{Spec}(A^{\prime })$
. We now have the following.
$\text{Spec}(A^{\prime })$
. We now have the following.
(1) The Hilbert polynomial for the pair
 $(X_{s},{\mathcal{O}}_{X_{s}}(1))$
is where the coefficients
$(X_{s},{\mathcal{O}}_{X_{s}}(1))$
is where the coefficients $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(X_{s},{\mathcal{O}}_{X_{s}}(m)) & = & \displaystyle \tilde{e}_{0}\binom{m+d-1}{d-1}-\tilde{e}_{1}\binom{m+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +(-1)^{d-1}\tilde{e}_{d-1},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(X_{s},{\mathcal{O}}_{X_{s}}(m)) & = & \displaystyle \tilde{e}_{0}\binom{m+d-1}{d-1}-\tilde{e}_{1}\binom{m+d-2}{d-2}\nonumber\\ \displaystyle & & \displaystyle +\cdots +(-1)^{d-1}\tilde{e}_{d-1},\nonumber\end{eqnarray}$$
 $\tilde{e}_{i}$
are as above for
$\tilde{e}_{i}$
are as above for
 $(X,{\mathcal{O}}_{X}(1))$
(from
$(X,{\mathcal{O}}_{X}(1))$
(from
 $\text{char}~0$
).
$\text{char}~0$
).In particular,
 $\dim ~X_{s}=d-1$
and we have the following.
$\dim ~X_{s}=d-1$
and we have the following.(2) By Remark 3.1, there exists
 $\bar{m}=P_{5}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1})$
such that
$\bar{m}=P_{5}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d-1})$
such that
 $(R_{s})_{m}=H^{0}(X_{s},{\mathcal{O}}_{X_{s}}(m))$
for all
$(R_{s})_{m}=H^{0}(X_{s},{\mathcal{O}}_{X_{s}}(m))$
for all
 $m\geqslant \bar{m}$
, and
$m\geqslant \bar{m}$
, and
 $(X_{s},{\mathcal{O}}_{X_{s}}(1))$
is
$(X_{s},{\mathcal{O}}_{X_{s}}(1))$
is
 $\bar{m}$
-regular.
$\bar{m}$
-regular.(3) Moreover, by the semicontinuity theorem (Chapter III, Theorem 12.8 in [H]), by shrinking
 $\text{Spec}(A^{\prime })$
further, we have
$\text{Spec}(A^{\prime })$
further, we have
 $h^{i}(X_{s},{\mathcal{O}}_{X_{s}}(\bar{m}))$
, and
$h^{i}(X_{s},{\mathcal{O}}_{X_{s}}(\bar{m}))$
, and
 $h^{0}(X_{s},{\mathcal{O}}_{X_{s}})$
is independent of
$h^{0}(X_{s},{\mathcal{O}}_{X_{s}})$
is independent of
 $s$
, for all
$s$
, for all
 $i\geqslant 0$
.
$i\geqslant 0$
.(4) Again, by shrinking
 $\text{Spec}(A^{\prime })$
(if necessary), can choose
$\text{Spec}(A^{\prime })$
(if necessary), can choose
 $n_{0}\in \mathbb{N}$
such that
$n_{0}\in \mathbb{N}$
such that
 $(R_{A^{\prime }})_{1}^{n_{0}}\subseteq I_{A^{\prime }}$
. This implies that
$(R_{A^{\prime }})_{1}^{n_{0}}\subseteq I_{A^{\prime }}$
. This implies that
 $(R_{s})_{1}^{n_{0}}\subseteq I_{s}$
, for all
$(R_{s})_{1}^{n_{0}}\subseteq I_{s}$
, for all
 $s\in \text{Spec}(A^{\prime })$
.
$s\in \text{Spec}(A^{\prime })$
.
Let
![]() $s\in \text{Spec}(A^{\prime })$
, and let
$s\in \text{Spec}(A^{\prime })$
, and let
![]() $p_{s}=\text{char}~k(s)$
. We sketch the proof of the existence of the map
$p_{s}=\text{char}~k(s)$
. We sketch the proof of the existence of the map
![]() $f_{R_{s},I_{s}}:[1,\infty )\rightarrow \mathbb{R}$
and its relation to
$f_{R_{s},I_{s}}:[1,\infty )\rightarrow \mathbb{R}$
and its relation to
![]() $e_{HK}(R,I)$
(note that we have proved this in a more general setting in [Reference TrivediT4]). By Proposition 2.11, for any given
$e_{HK}(R,I)$
(note that we have proved this in a more general setting in [Reference TrivediT4]). By Proposition 2.11, for any given
![]() $s$
, the sequence
$s$
, the sequence
![]() ${\{f_{n}^{s}\}}_{n}$
of functions is uniformly convergent. Let
${\{f_{n}^{s}\}}_{n}$
of functions is uniformly convergent. Let
![]() $f_{R_{s},I_{s}}(x)=\lim _{n\rightarrow \infty }f_{n}(R_{s},I_{s})(x)$
. This implies that
$f_{R_{s},I_{s}}(x)=\lim _{n\rightarrow \infty }f_{n}(R_{s},I_{s})(x)$
. This implies that
![]() $\lim _{n\rightarrow \infty }\int _{1}^{\infty }f_{n}(R_{s},I_{s})(x)=\int _{1}^{\infty }f_{R_{s},I_{s}}(x)$
, as, by Lemma 2.10, there is a compact set containing
$\lim _{n\rightarrow \infty }\int _{1}^{\infty }f_{n}(R_{s},I_{s})(x)=\int _{1}^{\infty }f_{R_{s},I_{s}}(x)$
, as, by Lemma 2.10, there is a compact set containing
![]() $\cup _{n}\text{supp}~f_{n}(R_{s},I_{s})$
. On the other hand,
$\cup _{n}\text{supp}~f_{n}(R_{s},I_{s})$
. On the other hand,
 $$\begin{eqnarray}\displaystyle e_{HK}(R_{s},I_{s}) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n}]}}\right)\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{\mathbf{m}_{s}^{p_{s}^{n}}}\right)+\lim _{n\rightarrow \infty }\frac{1}{p_{s}^{nd}}\mathop{\sum }_{m\geqslant 0}\ell \left(\frac{R}{I_{s}^{[p_{s}^{n}]}}\right)_{m+p_{s}^{n}}\nonumber\\ \displaystyle & = & \displaystyle \frac{e_{0}(R_{s})}{d!}+\lim _{n\rightarrow \infty }\int _{1}^{\infty }f_{n}(R_{s},I_{s})(x)\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{e_{0}(R_{s})}{d!}+\int _{1}^{\infty }f_{R_{s},I_{s}}(x)\,dx,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{HK}(R_{s},I_{s}) & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n}]}}\right)\nonumber\\ \displaystyle & = & \displaystyle \lim _{n\rightarrow \infty }\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{\mathbf{m}_{s}^{p_{s}^{n}}}\right)+\lim _{n\rightarrow \infty }\frac{1}{p_{s}^{nd}}\mathop{\sum }_{m\geqslant 0}\ell \left(\frac{R}{I_{s}^{[p_{s}^{n}]}}\right)_{m+p_{s}^{n}}\nonumber\\ \displaystyle & = & \displaystyle \frac{e_{0}(R_{s})}{d!}+\lim _{n\rightarrow \infty }\int _{1}^{\infty }f_{n}(R_{s},I_{s})(x)\,dx\nonumber\\ \displaystyle & = & \displaystyle \frac{e_{0}(R_{s})}{d!}+\int _{1}^{\infty }f_{R_{s},I_{s}}(x)\,dx,\nonumber\end{eqnarray}$$
where
![]() $\mathbf{m}_{s}$
is the graded maximal ideal of
$\mathbf{m}_{s}$
is the graded maximal ideal of
![]() $R_{s}$
and
$R_{s}$
and
![]() $e_{0}(R_{s})$
denotes the Hilbert–Samuel multiplicity of
$e_{0}(R_{s})$
denotes the Hilbert–Samuel multiplicity of
![]() $R_{s}$
with respect to
$R_{s}$
with respect to
![]() $\mathbf{m}_{s}$
.
$\mathbf{m}_{s}$
.
Now, by Proposition 2.11, there exists a constant
 $$\begin{eqnarray}C=2C_{R_{s}}+\unicode[STIX]{x1D707}\left(\bar{m}+n_{0}\left(\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D707}}d_{i}\right)+1\right)^{d-2}(\bar{P}_{1}^{d}+d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{3}^{d}),\end{eqnarray}$$
$$\begin{eqnarray}C=2C_{R_{s}}+\unicode[STIX]{x1D707}\left(\bar{m}+n_{0}\left(\mathop{\sum }_{i=1}^{\unicode[STIX]{x1D707}}d_{i}\right)+1\right)^{d-2}(\bar{P}_{1}^{d}+d^{d-1}\bar{P}_{2}^{d}+\bar{P}_{3}^{d}),\end{eqnarray}$$
which is independent of the choice of
![]() $s$
in
$s$
in
![]() $\text{Spec}(A^{\prime })$
(as
$\text{Spec}(A^{\prime })$
(as
![]() $C_{R_{s}}=\unicode[STIX]{x1D707}h^{0}(X_{s},{\mathcal{O}}_{X_{s}}(1))$
), such that
$C_{R_{s}}=\unicode[STIX]{x1D707}h^{0}(X_{s},{\mathcal{O}}_{X_{s}}(1))$
), such that
In particular, for given
![]() $m\geqslant d-1$
,
$m\geqslant d-1$
,
As
![]() $s\rightarrow s_{0}$
, we have
$s\rightarrow s_{0}$
, we have
![]() $p_{s}=\text{char}~k(s)\rightarrow \infty$
, which implies
$p_{s}=\text{char}~k(s)\rightarrow \infty$
, which implies
This completes the proof of Assertion (1) of the theorem.
It is easy to check that there exists a universal polynomial function
![]() $\bar{P}_{9}^{d}(X_{0},\ldots ,X_{d})$
with rational coefficients such that for
$\bar{P}_{9}^{d}(X_{0},\ldots ,X_{d})$
with rational coefficients such that for
![]() $C_{2}:=\bar{P}_{9}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d})$
we have
$C_{2}:=\bar{P}_{9}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{d})$
we have
Moreover, for every
![]() $n\geqslant 1$
, the function
$n\geqslant 1$
, the function
![]() $f_{n}(R_{s},I_{s})$
has support in the compact interval
$f_{n}(R_{s},I_{s})$
has support in the compact interval
![]() $[1,n_{0}\unicode[STIX]{x1D707}]$
. Therefore,
$[1,n_{0}\unicode[STIX]{x1D707}]$
. Therefore,
 $$\begin{eqnarray}\displaystyle (A_{1}) & := & \displaystyle \left|\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n}]}}\right)-\frac{1}{p_{s}^{(n+1)d}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n+1}]}}\right)\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left|\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{\mathbf{m}_{s}^{p_{s}^{n}}}\right)-\frac{e_{0}(R_{s})}{d!}\right|\nonumber\\ \displaystyle & & \displaystyle +\,\int _{1}^{n_{0}\unicode[STIX]{x1D707}}|f_{n}(R_{s},I_{s})(x)-f_{n+1}(R_{s},I_{s})(x)|\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (A_{1}) & := & \displaystyle \left|\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n}]}}\right)-\frac{1}{p_{s}^{(n+1)d}}\ell \left(\frac{R_{s}}{I_{s}^{[p_{s}^{n+1}]}}\right)\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \left|\frac{1}{p_{s}^{nd}}\ell \left(\frac{R_{s}}{\mathbf{m}_{s}^{p_{s}^{n}}}\right)-\frac{e_{0}(R_{s})}{d!}\right|\nonumber\\ \displaystyle & & \displaystyle +\,\int _{1}^{n_{0}\unicode[STIX]{x1D707}}|f_{n}(R_{s},I_{s})(x)-f_{n+1}(R_{s},I_{s})(x)|\,dx.\nonumber\end{eqnarray}$$
By (13), we have
This proves Assertion (2). Now, similarly, Assertion (3) easily follows from (14).◻
4 Some properties and examples
Throughout this section,
![]() $R$
is a standard graded integral domain of dimension
$R$
is a standard graded integral domain of dimension
![]() $d\geqslant 2$
, with
$d\geqslant 2$
, with
![]() $R_{0}=k$
, where
$R_{0}=k$
, where
![]() $k$
is an algebraically closed field of characteristic
$k$
is an algebraically closed field of characteristic
![]() $0$
, and
$0$
, and
![]() $I\subset R$
is a homogeneous ideal of finite colength. Our choice of spread satisfies conditions as given in Remark 3.4.
$I\subset R$
is a homogeneous ideal of finite colength. Our choice of spread satisfies conditions as given in Remark 3.4.
Definition 4.1. We denote
![]() $f_{R,I}^{\infty }=\lim _{p_{s}\rightarrow \infty }f_{R_{s},I_{s}}$
, if it exists, where for
$f_{R,I}^{\infty }=\lim _{p_{s}\rightarrow \infty }f_{R_{s},I_{s}}$
, if it exists, where for
![]() $(R,I)$
, the pair
$(R,I)$
, the pair
![]() $(R_{s},I_{s})$
is given as in Definition 3.2 and Notations 3.3.
$(R_{s},I_{s})$
is given as in Definition 3.2 and Notations 3.3.
Definition 4.2. For a choice of spread
![]() $(A,R_{A},I_{A})$
of
$(A,R_{A},I_{A})$
of
![]() $(R,I)$
, as in Remark 3.4, and a closed point
$(R,I)$
, as in Remark 3.4, and a closed point
![]() $s\in \text{Spec}(A)$
, we define
$s\in \text{Spec}(A)$
, we define
![]() $F_{R_{s}}:[0,\infty )\longrightarrow [0,\infty )$
as
$F_{R_{s}}:[0,\infty )\longrightarrow [0,\infty )$
as
 $$\begin{eqnarray}\displaystyle & \displaystyle HSd(R_{s})(x)=F_{R_{s}}(x)=\lim _{n\rightarrow \infty }F_{n}(R_{s})(x), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{where}\quad F_{n}(R_{s})(x)=\frac{1}{q^{d-1}}\ell (R_{s})_{\lfloor xq\rfloor }~\text{and}~q=p_{s}^{n}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle HSd(R_{s})(x)=F_{R_{s}}(x)=\lim _{n\rightarrow \infty }F_{n}(R_{s})(x), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{where}\quad F_{n}(R_{s})(x)=\frac{1}{q^{d-1}}\ell (R_{s})_{\lfloor xq\rfloor }~\text{and}~q=p_{s}^{n}. & \displaystyle \nonumber\end{eqnarray}$$
One can check that
where
![]() $e_{0}(R)$
is the Hilbert–Samuel multiplicity of
$e_{0}(R)$
is the Hilbert–Samuel multiplicity of
![]() $R$
with respect to
$R$
with respect to
![]() $\mathbf{m}$
. Hence, we denote
$\mathbf{m}$
. Hence, we denote
![]() $F_{R_{s}}(x)=F_{R}(x)$
. Moreover, for any
$F_{R_{s}}(x)=F_{R}(x)$
. Moreover, for any
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
![]() $\lim _{p_{s}\rightarrow \infty }F_{n}(R_{s})(x)=F_{R_{s}}(x)=F_{R}(x)$
.
$\lim _{p_{s}\rightarrow \infty }F_{n}(R_{s})(x)=F_{R_{s}}(x)=F_{R}(x)$
.
Proposition 4.3. Let
![]() $R$
and
$R$
and
![]() $S$
be standard graded domains, where
$S$
be standard graded domains, where
![]() $R_{0}=S_{0}=k$
, where
$R_{0}=S_{0}=k$
, where
![]() $k$
is an algebraically closed field of characteristic
$k$
is an algebraically closed field of characteristic
![]() $0$
with
$0$
with
![]() $I\subset R$
and
$I\subset R$
and
![]() $J\subset S$
homogeneous ideals of finite colength, respectively. Then,
$J\subset S$
homogeneous ideals of finite colength, respectively. Then,
where
![]() $R\#S=\oplus _{m\geqslant 0}R_{m}\otimes _{k}S_{m}$
. Moreover, in that case, we have
$R\#S=\oplus _{m\geqslant 0}R_{m}\otimes _{k}S_{m}$
. Moreover, in that case, we have
In particular,
![]() $f_{-,-}^{\infty }$
satisfies a multiplicative formula on Segre products.
$f_{-,-}^{\infty }$
satisfies a multiplicative formula on Segre products.
Proof. Let us denote
![]() $f^{\infty }=f_{R,I}^{\infty }$
and
$f^{\infty }=f_{R,I}^{\infty }$
and
![]() $g^{\infty }=f_{S,J}^{\infty }$
. For
$g^{\infty }=f_{S,J}^{\infty }$
. For
![]() $q=p_{s}^{n}$
, where
$q=p_{s}^{n}$
, where
![]() $p_{s}=\text{char}~k(s)$
, we denote
$p_{s}=\text{char}~k(s)$
, we denote
![]() $f_{n}^{s}=f_{n}(R_{s},I_{s})$
and
$f_{n}^{s}=f_{n}(R_{s},I_{s})$
and
![]() $g_{n}^{s}=f_{n}(S_{s},J_{s})$
, where
$g_{n}^{s}=f_{n}(S_{s},J_{s})$
, where
![]() $s\in \text{Spec}(A)$
denotes a closed point and
$s\in \text{Spec}(A)$
denotes a closed point and
![]() $(A,R_{A},I_{A})$
and
$(A,R_{A},I_{A})$
and
![]() $(A,S_{A},J_{A})$
are spreads.
$(A,S_{A},J_{A})$
are spreads.
For any
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
For a spread
![]() $(A,R_{A},I_{A})$
, let
$(A,R_{A},I_{A})$
, let
![]() $n_{0}$
and
$n_{0}$
and
![]() $\unicode[STIX]{x1D707}$
be positive integers such that
$\unicode[STIX]{x1D707}$
be positive integers such that
![]() ${(R_{A})_{1}}^{n_{0}}\subseteq I_{A}$
and
${(R_{A})_{1}}^{n_{0}}\subseteq I_{A}$
and
![]() ${(S_{A})_{1}}^{n_{0}}\subseteq J_{A}$
, and also
${(S_{A})_{1}}^{n_{0}}\subseteq J_{A}$
, and also
![]() $\unicode[STIX]{x1D707}(I_{A})$
,
$\unicode[STIX]{x1D707}(I_{A})$
,
![]() $\unicode[STIX]{x1D707}(J_{A})\leqslant \unicode[STIX]{x1D707}$
. Then, by Lemma 2.10,
$\unicode[STIX]{x1D707}(J_{A})\leqslant \unicode[STIX]{x1D707}$
. Then, by Lemma 2.10,
Moreover, there is a constant
![]() $C_{1}$
such that, for any
$C_{1}$
such that, for any
![]() $n\geqslant 1$
and every closed point
$n\geqslant 1$
and every closed point
![]() $s\in \text{Spec}(A)$
, we have
$s\in \text{Spec}(A)$
, we have
for all
![]() $x\in [1,n_{0}\unicode[STIX]{x1D707}]$
.
$x\in [1,n_{0}\unicode[STIX]{x1D707}]$
.
Since
![]() $f^{\infty }$
and
$f^{\infty }$
and
![]() $g^{\infty }$
exist, by Theorem 1.1(1), for given
$g^{\infty }$
exist, by Theorem 1.1(1), for given
![]() $n\geqslant d_{1}+d_{1}-2$
, we have
$n\geqslant d_{1}+d_{1}-2$
, we have
Therefore, by (15), for given
![]() $n\geqslant d_{1}+d_{2}-2$
, we have
$n\geqslant d_{1}+d_{2}-2$
, we have
Hence, for any
![]() $n\geqslant d_{1}+d_{2}-2$
,
$n\geqslant d_{1}+d_{2}-2$
,
Now, by Theorem 1.1(1), the proposition follows. ◻
Proposition 4.4. Let the pairs
![]() $(R,I)$
and
$(R,I)$
and
![]() $(S,J)$
be as in Proposition 4.3. Let
$(S,J)$
be as in Proposition 4.3. Let
![]() $(A,R_{A},I_{A})$
,
$(A,R_{A},I_{A})$
,
![]() $(A,S_{A},J_{A})$
be spreads for
$(A,S_{A},J_{A})$
be spreads for
![]() $(R,I)$
and
$(R,I)$
and
![]() $(S,J)$
, respectively, and let
$(S,J)$
, respectively, and let
![]() $s\in \text{Spec}(A)$
be a closed point. Suppose that
$s\in \text{Spec}(A)$
be a closed point. Suppose that
![]() $f_{R_{s},I_{s}}\geqslant f_{R,I}^{\infty }$
and
$f_{R_{s},I_{s}}\geqslant f_{R,I}^{\infty }$
and
![]() $f_{S_{s},J_{s}}\geqslant f_{S,J}^{\infty }$
. Then,
$f_{S_{s},J_{s}}\geqslant f_{S,J}^{\infty }$
. Then,
(1)
 $f_{R_{s}\#S_{s},I_{s}\#J_{s}}\geqslant f_{R\#S,I\#J}^{\infty }$
. Moreover,
$f_{R_{s}\#S_{s},I_{s}\#J_{s}}\geqslant f_{R\#S,I\#J}^{\infty }$
. Moreover,(2) if in addition
 $I_{s}\cap (R_{s})_{1}\neq 0$
and
$I_{s}\cap (R_{s})_{1}\neq 0$
and
 $J_{s}\cap (S_{s})_{1}\neq 0$
, then
$J_{s}\cap (S_{s})_{1}\neq 0$
, then  $$\begin{eqnarray}f_{R_{s},I_{s}}=f_{R,I}^{\infty }\quad \text{and}\quad f_{S_{s},J_{s}}=f_{S,J}^{\infty }\quad \!\;\Longleftrightarrow \;f_{R_{s}\#S_{s},I_{s}\#J_{s}}=f_{R\#S,I\#J}^{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}f_{R_{s},I_{s}}=f_{R,I}^{\infty }\quad \text{and}\quad f_{S_{s},J_{s}}=f_{S,J}^{\infty }\quad \!\;\Longleftrightarrow \;f_{R_{s}\#S_{s},I_{s}\#J_{s}}=f_{R\#S,I\#J}^{\infty }.\end{eqnarray}$$
Proof. (1) Let us denote
![]() $f^{\infty }=f_{R,I}^{\infty }$
and
$f^{\infty }=f_{R,I}^{\infty }$
and
![]() $g^{\infty }=g^{\infty }(S,J)$
, and denote
$g^{\infty }=g^{\infty }(S,J)$
, and denote
![]() $f^{s}=f_{R_{s},I_{s}}$
and
$f^{s}=f_{R_{s},I_{s}}$
and
![]() $g^{s}=f_{S_{s},J_{s}}$
.
$g^{s}=f_{S_{s},J_{s}}$
.
We know, by the multiplicative property of the HK density functions (see [Reference TrivediT4, Proposition 2.18]), that
 $$\begin{eqnarray}\displaystyle f_{R_{s}\#S_{s},I_{s}\#J_{s}}(x) & = & \displaystyle F_{R}(x)g^{s}(x)+F_{S}(x)f^{s}(x)-f^{s}(x)g^{s}(x)\nonumber\\ \displaystyle & = & \displaystyle (F_{R}(x)-f^{s}(x))g^{s}(x)+F_{S}(x)f^{s}(x)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (F_{R}(x)-f^{s}(x))g^{\infty }(x)+F_{S}(x)f^{s}(x)\nonumber\\ \displaystyle & = & \displaystyle F_{R}(x)g^{\infty }(x)+f^{s}(x)[F_{S}(x)-g^{\infty }(x)]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle F_{R}(x)g^{\infty }(x)+f^{\infty }(x)[F_{S}(x)-g^{\infty }(x)]\nonumber\\ \displaystyle & = & \displaystyle f_{R\#S,I\#J}^{\infty }(x),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{R_{s}\#S_{s},I_{s}\#J_{s}}(x) & = & \displaystyle F_{R}(x)g^{s}(x)+F_{S}(x)f^{s}(x)-f^{s}(x)g^{s}(x)\nonumber\\ \displaystyle & = & \displaystyle (F_{R}(x)-f^{s}(x))g^{s}(x)+F_{S}(x)f^{s}(x)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (F_{R}(x)-f^{s}(x))g^{\infty }(x)+F_{S}(x)f^{s}(x)\nonumber\\ \displaystyle & = & \displaystyle F_{R}(x)g^{\infty }(x)+f^{s}(x)[F_{S}(x)-g^{\infty }(x)]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle F_{R}(x)g^{\infty }(x)+f^{\infty }(x)[F_{S}(x)-g^{\infty }(x)]\nonumber\\ \displaystyle & = & \displaystyle f_{R\#S,I\#J}^{\infty }(x),\nonumber\end{eqnarray}$$
where the third and fifth inequalities hold as
![]() $F_{R}(x)\geqslant f^{s}(x)$
and
$F_{R}(x)\geqslant f^{s}(x)$
and
![]() $F_{S}(x)\geqslant g^{s}(x)$
, for every
$F_{S}(x)\geqslant g^{s}(x)$
, for every
![]() $s\in \text{Spec}\,A$
, and the last equality follows from Proposition 4.3.
$s\in \text{Spec}\,A$
, and the last equality follows from Proposition 4.3.
(2) Suppose that
![]() $I$
and
$I$
and
![]() $J$
are the ideals of
$J$
are the ideals of
![]() $R$
and
$R$
and
![]() $S$
, respectively, and
$S$
, respectively, and
![]() $s\in \text{Spec}(A)$
is a closed point such that
$s\in \text{Spec}(A)$
is a closed point such that
![]() $I_{s}\cap (R_{s})_{1}\neq 0$
and
$I_{s}\cap (R_{s})_{1}\neq 0$
and
![]() $J_{s}\cap (S_{s})_{1}\neq 0$
. Then, we make the following claim.
$J_{s}\cap (S_{s})_{1}\neq 0$
. Then, we make the following claim.
Claim.
![]() $F_{R}(x)>f^{s}(x)$
and
$F_{R}(x)>f^{s}(x)$
and
![]() $G_{S}(x)>g^{s}(x)$
, for all
$G_{S}(x)>g^{s}(x)$
, for all
![]() $x\geqslant 1$
.
$x\geqslant 1$
.
Proof of the Claim. It is sufficient to prove that
![]() $F_{R}(x+1)>f^{s}(x+1)$
, for
$F_{R}(x+1)>f^{s}(x+1)$
, for
![]() $x>0$
. Choose an integer
$x>0$
. Choose an integer
![]() $n_{0}$
such that
$n_{0}$
such that
![]() $x\geqslant 1/p_{s}^{n_{0}}$
, where
$x\geqslant 1/p_{s}^{n_{0}}$
, where
![]() $p_{s}=\text{char}~k(s)$
. Let
$p_{s}=\text{char}~k(s)$
. Let
![]() $q=p_{s}^{n}$
for some
$q=p_{s}^{n}$
for some
![]() $n$
. For a given nonzero
$n$
. For a given nonzero
![]() $y\in I_{s}\cap (R_{s})_{1}$
, we have an injective map of the
$y\in I_{s}\cap (R_{s})_{1}$
, we have an injective map of the
![]() $R_{s}$
-linear map (
$R_{s}$
-linear map (
![]() $R$
is a domain)
$R$
is a domain)
![]() $\oplus _{m\geqslant 0}{(R_{s})_{m}\longrightarrow \oplus }_{m\geqslant 0}(I_{s}^{[q]})_{m+q},$
of degree
$\oplus _{m\geqslant 0}{(R_{s})_{m}\longrightarrow \oplus }_{m\geqslant 0}(I_{s}^{[q]})_{m+q},$
of degree
![]() $q$
, given by the multiplication by element
$q$
, given by the multiplication by element
![]() $y^{q}$
. Therefore,
$y^{q}$
. Therefore,
![]() $\ell (I_{s}^{[q]})_{m+q}\geqslant \ell (R_{s})_{m}$
, for all
$\ell (I_{s}^{[q]})_{m+q}\geqslant \ell (R_{s})_{m}$
, for all
![]() $m\geqslant 0$
. Since
$m\geqslant 0$
. Since
![]() $\lfloor xq\rfloor =m$
if and only if
$\lfloor xq\rfloor =m$
if and only if
![]() $\lfloor (x+1)q\rfloor =m+q$
, we have
$\lfloor (x+1)q\rfloor =m+q$
, we have
![]() $\ell (I_{s}^{[q]})_{\lfloor (x+1)q\rfloor }\geqslant \ell (R_{s})_{\lfloor xq\rfloor }$
. Hence,
$\ell (I_{s}^{[q]})_{\lfloor (x+1)q\rfloor }\geqslant \ell (R_{s})_{\lfloor xq\rfloor }$
. Hence,
![]() $\ell (R_{s}/I_{s}^{[q]})_{\lfloor (x+1)q\rfloor }\leqslant \ell (R_{s})_{\lfloor (x+1)q\rfloor }-\ell (R_{s})_{\lfloor xq\rfloor }$
.
$\ell (R_{s}/I_{s}^{[q]})_{\lfloor (x+1)q\rfloor }\leqslant \ell (R_{s})_{\lfloor (x+1)q\rfloor }-\ell (R_{s})_{\lfloor xq\rfloor }$
.
Therefore,
![]() $f_{n}(R_{s},I_{s})(x+1)\leqslant F_{n}(R_{s})(x+1)-F_{n}(R_{s})(x)$
.
$f_{n}(R_{s},I_{s})(x+1)\leqslant F_{n}(R_{s})(x+1)-F_{n}(R_{s})(x)$
.
However,
where
![]() $d=\dim R$
. This implies that
$d=\dim R$
. This implies that
![]() $f^{s}(x+1)=f_{R_{s},I_{s}}(x+1)<F_{R}(x+1)$
. This proves the claim.
$f^{s}(x+1)=f_{R_{s},I_{s}}(x+1)<F_{R}(x+1)$
. This proves the claim.
Now, retracing the above argument, we note that
![]() $f_{R_{s}\#S_{s},I_{s}\#J_{s}}=f_{R\#S,I\#J}^{\infty }$
if and only if
$f_{R_{s}\#S_{s},I_{s}\#J_{s}}=f_{R\#S,I\#J}^{\infty }$
if and only if
and
Hence, by the above claim, we have
![]() $f^{s}(x)=f^{\infty }(x)$
and
$f^{s}(x)=f^{\infty }(x)$
and
![]() $g^{s}(x)=g^{\infty }(x)$
for all
$g^{s}(x)=g^{\infty }(x)$
for all
![]() $x>1$
. For
$x>1$
. For
![]() $x=1$
, we have
$x=1$
, we have
![]() $F_{R}(x)=f^{s}(x)=f^{\infty }(x)$
and
$F_{R}(x)=f^{s}(x)=f^{\infty }(x)$
and
![]() $F_{S}(x)=g^{s}(x)=g^{\infty }(x)$
. This proves the proposition.◻
$F_{S}(x)=g^{s}(x)=g^{\infty }(x)$
. This proves the proposition.◻
Example 4.5. Let
![]() $R$
be a two-dimensional standard graded normal domain, where
$R$
be a two-dimensional standard graded normal domain, where
![]() $R_{0}=k$
is an algebraically closed field of
$R_{0}=k$
is an algebraically closed field of
![]() $\text{char}~0$
. Let
$\text{char}~0$
. Let
![]() $I=\mathbf{m}\subset R$
be the graded maximal ideal of
$I=\mathbf{m}\subset R$
be the graded maximal ideal of
![]() $R$
generated by
$R$
generated by
![]() $h_{1},\ldots ,h_{\unicode[STIX]{x1D707}}$
of degree
$h_{1},\ldots ,h_{\unicode[STIX]{x1D707}}$
of degree
![]() $1$
. Let
$1$
. Let
![]() $X=\text{Proj}~R$
be the corresponding nonsingular projective curve, and let
$X=\text{Proj}~R$
be the corresponding nonsingular projective curve, and let
be the canonical short exact sequence of locally free sheaves of
![]() ${\mathcal{O}}_{X}$
-modules. (Moreover, the sequence is locally split exact.)
${\mathcal{O}}_{X}$
-modules. (Moreover, the sequence is locally split exact.)
Let
![]() $(A,R_{A},I_{A})$
and
$(A,R_{A},I_{A})$
and
![]() $(A,X_{A},V_{A})$
denote spreads for
$(A,X_{A},V_{A})$
denote spreads for
![]() $(R,I)$
and
$(R,I)$
and
![]() $(X,V)$
, respectively. Then, we have an associated canonical exact sequence of locally free sheaves of
$(X,V)$
, respectively. Then, we have an associated canonical exact sequence of locally free sheaves of
![]() ${\mathcal{O}}_{X_{A}}$
-modules
${\mathcal{O}}_{X_{A}}$
-modules
Restricting to the fiber
![]() $X_{s}$
, we have the following exact sequence of locally free sheaves of
$X_{s}$
, we have the following exact sequence of locally free sheaves of
![]() ${\mathcal{O}}_{X_{s}}$
-modules:
${\mathcal{O}}_{X_{s}}$
-modules:
Moreover, we can choose a spread
![]() $(A,X_{A},V_{A})$
such that there is a filtration
$(A,X_{A},V_{A})$
such that there is a filtration
of locally free sheaves of
![]() ${\mathcal{O}}_{X_{A}}$
-modules such that
${\mathcal{O}}_{X_{A}}$
-modules such that
is the HN filtration of the vector bundles over
![]() $X_{s}$
for
$X_{s}$
for
![]() $s\in \text{Spec}~A$
.
$s\in \text{Spec}~A$
.
Theorem 4.6. Let
![]() $(R,I)$
,
$(R,I)$
,
![]() $(A,R_{A},I_{A})$
, and
$(A,R_{A},I_{A})$
, and
![]() $(A,X_{A},V_{A})$
be given as above. Then, for every closed point
$(A,X_{A},V_{A})$
be given as above. Then, for every closed point
![]() $s\in \text{Spec}(A)$
, we have
$s\in \text{Spec}(A)$
, we have
(1)
 $f_{R_{s},I_{s}}\geqslant f_{R,I}^{\infty }$
and
$f_{R_{s},I_{s}}\geqslant f_{R,I}^{\infty }$
and(2)
 $f_{R_{s},I_{s}}=f_{R,I}^{\infty }$
if and only if the filtration is the strongly semistable HN filtration of
$f_{R_{s},I_{s}}=f_{R,I}^{\infty }$
if and only if the filtration is the strongly semistable HN filtration of $$\begin{eqnarray}0=E_{0s}\subset E_{1s}\subset \cdots \subset E_{ls}\subset E_{l+1s}=V_{s}\end{eqnarray}$$
$$\begin{eqnarray}0=E_{0s}\subset E_{1s}\subset \cdots \subset E_{ls}\subset E_{l+1s}=V_{s}\end{eqnarray}$$
 $V_{s}$
on
$V_{s}$
on
 $X_{s}$
. That is, for every
$X_{s}$
. That is, for every
 $n\geqslant 1$
, is the HN filtration of
$n\geqslant 1$
, is the HN filtration of $$\begin{eqnarray}0=F^{n\ast }E_{0s}\subset F^{n\ast }E_{1s}\subset \cdots \subset F^{n\ast }E_{ls}\subset F^{n\ast }E_{l+1s}=F^{n\ast }V_{s}\end{eqnarray}$$
$$\begin{eqnarray}0=F^{n\ast }E_{0s}\subset F^{n\ast }E_{1s}\subset \cdots \subset F^{n\ast }E_{ls}\subset F^{n\ast }E_{l+1s}=F^{n\ast }V_{s}\end{eqnarray}$$
 $F^{n\ast }V_{s}$
.
$F^{n\ast }V_{s}$
.
Proof. We fix such an
![]() $s\in \text{Spec}~A$
and let
$s\in \text{Spec}~A$
and let
![]() $d=\deg X_{s}$
(
$d=\deg X_{s}$
(
![]() $d$
independent of
$d$
independent of
![]() $s$
), and let the HN filtration of
$s$
), and let the HN filtration of
![]() $V_{s}$
be
$V_{s}$
be
By [Reference LangerL, Theorem 2.7], there is
![]() $n_{1}\geqslant 1$
such that
$n_{1}\geqslant 1$
such that
![]() $F^{n_{1}\ast }V_{s}$
has the strong HN filtration. (Note that
$F^{n_{1}\ast }V_{s}$
has the strong HN filtration. (Note that
![]() $n_{1}$
may depend on
$n_{1}$
may depend on
![]() $s$
.)
$s$
.)
Then, by [Reference TrivediT2, Lemma 1.8], for
![]() $p_{s}=\text{char}~k(s)>4(\text{genus}(X_{s}))\text{rank}(V_{s})^{3}$
, the HN filtration of
$p_{s}=\text{char}~k(s)>4(\text{genus}(X_{s}))\text{rank}(V_{s})^{3}$
, the HN filtration of
![]() $F^{n_{1}\ast }V_{s}$
is
$F^{n_{1}\ast }V_{s}$
is
 $$\begin{eqnarray}\displaystyle & 0=E_{00}\subset E_{01}\subset \cdots \subset E_{0t_{0}}\subset E_{0,(t_{0}+1)}=F^{n_{1}\ast }E_{1}=E_{10}\subset \cdots \subset & \displaystyle \nonumber\\ \displaystyle & E_{i-1(t_{i-1}+1)}=F^{n_{1}\ast }E_{i}=E_{i0}\subset E_{i1}\subset \cdots \subset E_{it_{i}}\subset E_{i(t_{i}+1)} & \displaystyle \nonumber\\ \displaystyle & E_{i(t_{i}+1)}=F^{n_{1}\ast }E_{i+1}=E_{i+1,0}\subset \cdots \subset F^{n_{1}\ast }V_{s}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & 0=E_{00}\subset E_{01}\subset \cdots \subset E_{0t_{0}}\subset E_{0,(t_{0}+1)}=F^{n_{1}\ast }E_{1}=E_{10}\subset \cdots \subset & \displaystyle \nonumber\\ \displaystyle & E_{i-1(t_{i-1}+1)}=F^{n_{1}\ast }E_{i}=E_{i0}\subset E_{i1}\subset \cdots \subset E_{it_{i}}\subset E_{i(t_{i}+1)} & \displaystyle \nonumber\\ \displaystyle & E_{i(t_{i}+1)}=F^{n_{1}\ast }E_{i+1}=E_{i+1,0}\subset \cdots \subset F^{n_{1}\ast }V_{s}. & \displaystyle \nonumber\end{eqnarray}$$
Let, for
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $j\geqslant 1$
,
$j\geqslant 1$
,
Let
Note that, for any
![]() $i\geqslant 1$
, the only possible inequalities are
$i\geqslant 1$
, the only possible inequalities are
and also note that
![]() $a_{ij}\leqslant 0$
. By [Reference TrivediT2, Lemma 1.14], for a given
$a_{ij}\leqslant 0$
. By [Reference TrivediT2, Lemma 1.14], for a given
![]() $i$
,
$i$
,
where, by
![]() $O(1/p_{s})$
, we mean
$O(1/p_{s})$
, we mean
![]() $O(1/p_{s})=C/p_{s}$
, where
$O(1/p_{s})=C/p_{s}$
, where
![]() $|C|$
is bounded by a constant depending only on the degree of
$|C|$
is bounded by a constant depending only on the degree of
![]() $X$
and rank of
$X$
and rank of
![]() $V$
(and hence is independent of
$V$
(and hence is independent of
![]() $p_{s}$
).
$p_{s}$
).
Claim. If
![]() $1-a_{ij_{0}}/d\leqslant x<1-a_{i(j_{0}+1)}/d$
, for some
$1-a_{ij_{0}}/d\leqslant x<1-a_{i(j_{0}+1)}/d$
, for some
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
![]() $j_{0}\geqslant 1$
, then we have the following.
$j_{0}\geqslant 1$
, then we have the following.
(1)
 $-[a_{ij}r_{ij}+d(x-1)r_{ij}]=-[\unicode[STIX]{x1D707}_{i+1}r_{ij}+d(x-1)r_{ij}]+O(1/p_{s})$
, for any
$-[a_{ij}r_{ij}+d(x-1)r_{ij}]=-[\unicode[STIX]{x1D707}_{i+1}r_{ij}+d(x-1)r_{ij}]+O(1/p_{s})$
, for any
 $1\leqslant k\leqslant t_{i}+1$
, and
$1\leqslant k\leqslant t_{i}+1$
, and
 $-[a_{ij}r_{ij}+d(x-1)r_{ij}]\leqslant 0$
if
$-[a_{ij}r_{ij}+d(x-1)r_{ij}]\leqslant 0$
if
 $k\leqslant j_{0}$
.
$k\leqslant j_{0}$
.(2)
 $-\sum _{k\geqslant j_{0}+1}[a_{ik}r_{ik}+d(x-1)r_{ik}]\geqslant -[\unicode[STIX]{x1D707}_{i+1}r_{i+1}+d(x-1)r_{i+1}]$
.
$-\sum _{k\geqslant j_{0}+1}[a_{ik}r_{ik}+d(x-1)r_{ik}]\geqslant -[\unicode[STIX]{x1D707}_{i+1}r_{i+1}+d(x-1)r_{i+1}]$
.
We skip the proof of the claim.
We also recall that, for
![]() $x$
, as in the above claim, by [Reference TrivediT4, Example 3.3], we have
$x$
, as in the above claim, by [Reference TrivediT4, Example 3.3], we have
Let
![]() $x\geqslant 1$
; then,
$x\geqslant 1$
; then,
![]() $1-\unicode[STIX]{x1D707}_{i}/d\leqslant x<1-\unicode[STIX]{x1D707}_{i+1}/d$
, for some
$1-\unicode[STIX]{x1D707}_{i}/d\leqslant x<1-\unicode[STIX]{x1D707}_{i+1}/d$
, for some
![]() $i\geqslant 0$
. (Note that
$i\geqslant 0$
. (Note that
![]() $-\unicode[STIX]{x1D707}_{i}\geqslant 0$
.) Now, there are three possibilities.
$-\unicode[STIX]{x1D707}_{i}\geqslant 0$
.) Now, there are three possibilities.
(1)
 $1-\unicode[STIX]{x1D707}_{i}/d\leqslant x<1-a_{i-1,(t_{i-1}+1)}/d$
. Then, and
$1-\unicode[STIX]{x1D707}_{i}/d\leqslant x<1-a_{i-1,(t_{i-1}+1)}/d$
. Then, and $$\begin{eqnarray}1-\frac{a_{i-1,j_{0}}}{d}\leqslant x<1-\frac{a_{i-1,(j_{0}+1)}}{d},\quad \text{for some}~j_{0}\geqslant 1,\end{eqnarray}$$
Therefore, by the above claim part (2),
$$\begin{eqnarray}1-\frac{a_{i-1,j_{0}}}{d}\leqslant x<1-\frac{a_{i-1,(j_{0}+1)}}{d},\quad \text{for some}~j_{0}\geqslant 1,\end{eqnarray}$$
Therefore, by the above claim part (2), $$\begin{eqnarray}\displaystyle f_{R_{s},I_{s}}(x) & = & \displaystyle -\mathop{\sum }_{j\geqslant j_{0}+1}[a_{i-1,j}r_{i-1,j}+d(x-1)r_{i-1,j}]\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{k\geqslant i+2}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{R_{s},I_{s}}(x) & = & \displaystyle -\mathop{\sum }_{j\geqslant j_{0}+1}[a_{i-1,j}r_{i-1,j}+d(x-1)r_{i-1,j}]\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{k\geqslant i+2}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\nonumber\end{eqnarray}$$
 $$\begin{eqnarray}f_{R_{s},I_{s}}(x)\geqslant -\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
$$\begin{eqnarray}f_{R_{s},I_{s}}(x)\geqslant -\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
(2)
 $1-a_{i-1,(t_{i-1}+1)}/d\leqslant x<1-a_{i1}/d$
. Then,
$1-a_{i-1,(t_{i-1}+1)}/d\leqslant x<1-a_{i1}/d$
. Then,  $$\begin{eqnarray}f_{R_{s},I_{s}}(x)=-\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
$$\begin{eqnarray}f_{R_{s},I_{s}}(x)=-\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
(3)
 $1-a_{i1}/d\leqslant x<1-\unicode[STIX]{x1D707}_{i+1}/d$
. Then and
$1-a_{i1}/d\leqslant x<1-\unicode[STIX]{x1D707}_{i+1}/d$
. Then and $$\begin{eqnarray}1-\frac{a_{ij_{0}}}{d}\leqslant x<1-\frac{a_{i,(j_{0}+1)}}{d},\quad \text{for some}~j_{0}\geqslant 1,\end{eqnarray}$$
$$\begin{eqnarray}1-\frac{a_{ij_{0}}}{d}\leqslant x<1-\frac{a_{i,(j_{0}+1)}}{d},\quad \text{for some}~j_{0}\geqslant 1,\end{eqnarray}$$
 $$\begin{eqnarray}f_{R_{s},I_{s}}(x)=-\mathop{\sum }_{j\geqslant j_{0}+1}[a_{ij}r_{ij}+d(x-1)r_{ij}]-\mathop{\sum }_{k\geqslant i+2}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
$$\begin{eqnarray}f_{R_{s},I_{s}}(x)=-\mathop{\sum }_{j\geqslant j_{0}+1}[a_{ij}r_{ij}+d(x-1)r_{ij}]-\mathop{\sum }_{k\geqslant i+2}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
Therefore, again by the above claim part (2),
 $$\begin{eqnarray}f_{R_{s},I_{s}}(x)\geqslant -\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
$$\begin{eqnarray}f_{R_{s},I_{s}}(x)\geqslant -\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}].\end{eqnarray}$$
By (18), we have that
![]() $f_{R,I}^{\infty }=\lim _{p_{s}\rightarrow \infty }f_{R_{s},I_{s}}$
exists, and
$f_{R,I}^{\infty }=\lim _{p_{s}\rightarrow \infty }f_{R_{s},I_{s}}$
exists, and
 $$\begin{eqnarray}\begin{array}{@{}lcl@{}}1\leqslant x<1-\unicode[STIX]{x1D707}_{1}/d & \Rightarrow & f_{R,I}^{\infty }(x)=-\left[\displaystyle \mathop{\sum }_{i\geqslant 1}\unicode[STIX]{x1D707}_{i}r_{i}+d(x-1)r_{i}\right],\\ 1-\unicode[STIX]{x1D707}_{i}/d\leqslant x<1-\unicode[STIX]{x1D707}_{i+1}/d & \Rightarrow & f_{R,I}^{\infty }(x)=-\left[\displaystyle \mathop{\sum }_{k\geqslant i+1}\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}\right]\!.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}lcl@{}}1\leqslant x<1-\unicode[STIX]{x1D707}_{1}/d & \Rightarrow & f_{R,I}^{\infty }(x)=-\left[\displaystyle \mathop{\sum }_{i\geqslant 1}\unicode[STIX]{x1D707}_{i}r_{i}+d(x-1)r_{i}\right],\\ 1-\unicode[STIX]{x1D707}_{i}/d\leqslant x<1-\unicode[STIX]{x1D707}_{i+1}/d & \Rightarrow & f_{R,I}^{\infty }(x)=-\left[\displaystyle \mathop{\sum }_{k\geqslant i+1}\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}\right]\!.\end{array}\end{eqnarray}$$
This implies that
![]() $f_{R_{s},I_{s}}\geqslant f_{R,I}^{\infty }$
for
$f_{R_{s},I_{s}}\geqslant f_{R,I}^{\infty }$
for
![]() $1\leqslant x<1-a_{l,(t_{l}+1)}/d$
, and
$1\leqslant x<1-a_{l,(t_{l}+1)}/d$
, and
![]() $f_{R_{s},I_{s}}=f_{R,I}^{\infty }=0$
otherwise. This proves part (1) of the theorem.
$f_{R_{s},I_{s}}=f_{R,I}^{\infty }=0$
otherwise. This proves part (1) of the theorem.
(2) If
![]() $V_{s}$
has strongly semistable HN filtration, then it is obvious that
$V_{s}$
has strongly semistable HN filtration, then it is obvious that
![]() $f_{R_{s},I_{s}}=f_{R,I}^{\infty }$
. Let, as before,
$f_{R_{s},I_{s}}=f_{R,I}^{\infty }$
. Let, as before,
![]() $n_{1}$
be such that
$n_{1}$
be such that
![]() $F^{n_{1}\ast }V$
has a strongly semistable HN filtration in the sense of [Reference LangerL, Theorem 2.7].
$F^{n_{1}\ast }V$
has a strongly semistable HN filtration in the sense of [Reference LangerL, Theorem 2.7].
If the HN filtration of
![]() $V_{s}$
is not strongly semistable, then
$V_{s}$
is not strongly semistable, then
is not the HN filtration of
![]() $F^{n_{1}\ast }V$
. Therefore, there exists
$F^{n_{1}\ast }V$
. Therefore, there exists
![]() $i\geqslant 0$
such that
$i\geqslant 0$
such that
where
![]() $E_{i1}\subset F^{n_{1}\ast }E_{i+1}$
. Since
$E_{i1}\subset F^{n_{1}\ast }E_{i+1}$
. Since
![]() $a_{i1}>\unicode[STIX]{x1D707}_{i+1}$
, one can choose
$a_{i1}>\unicode[STIX]{x1D707}_{i+1}$
, one can choose
![]() $1-a_{i1}/d<x_{0}\leqslant 1-\unicode[STIX]{x1D707}_{i+1}/d\leqslant 1-a_{i2}/d$
. Now,
$1-a_{i1}/d<x_{0}\leqslant 1-\unicode[STIX]{x1D707}_{i+1}/d\leqslant 1-a_{i2}/d$
. Now,
 $$\begin{eqnarray}\displaystyle f_{R_{s},I_{s}}(x) & = & \displaystyle -\mathop{\sum }_{j\geqslant 2}\left[a_{ij}r_{ij}+d(x-1)r_{ij}\right]-\mathop{\sum }_{k\geqslant i+2}\left[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}\right].\nonumber\\ \displaystyle & = & \displaystyle [a_{i1}r_{i1}+d(x-1)r_{i1}]-\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}]>f_{R,I}^{\infty }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{R_{s},I_{s}}(x) & = & \displaystyle -\mathop{\sum }_{j\geqslant 2}\left[a_{ij}r_{ij}+d(x-1)r_{ij}\right]-\mathop{\sum }_{k\geqslant i+2}\left[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}\right].\nonumber\\ \displaystyle & = & \displaystyle [a_{i1}r_{i1}+d(x-1)r_{i1}]-\mathop{\sum }_{k\geqslant i+1}[\unicode[STIX]{x1D707}_{k}r_{k}+d(x-1)r_{k}]>f_{R,I}^{\infty }.\nonumber\end{eqnarray}$$
This proves the theorem. ◻
Corollary 4.7. Let
![]() $C_{1}=\text{Proj}~S_{1},\ldots ,C_{n}=\text{Proj}~S_{n}$
be nonsingular projective curves, over a common field of characteristic
$C_{1}=\text{Proj}~S_{1},\ldots ,C_{n}=\text{Proj}~S_{n}$
be nonsingular projective curves, over a common field of characteristic
![]() $0$
. Suppose that each syzygy bundle
$0$
. Suppose that each syzygy bundle
![]() $V_{C_{i}}$
, given by
$V_{C_{i}}$
, given by
is semistable. (For example, if
![]() $\deg {\mathcal{O}}_{C_{i}}(1)>2\text{genus}(C_{i})$
, then
$\deg {\mathcal{O}}_{C_{i}}(1)>2\text{genus}(C_{i})$
, then
![]() $V_{C_{i}}$
is semistable; see [Reference Paranjape and RamananPR] and [Reference TrivediT6, Lemma 2.1].)
$V_{C_{i}}$
is semistable; see [Reference Paranjape and RamananPR] and [Reference TrivediT6, Lemma 2.1].)
Then, there is
![]() $n_{0}$
such that for all
$n_{0}$
such that for all
![]() $p\geqslant n_{0}$
we have
$p\geqslant n_{0}$
we have
(1)
 $f_{(S_{1}\#\cdots \#S_{n})_{p}}(x)\geqslant f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x)$
and
$f_{(S_{1}\#\cdots \#S_{n})_{p}}(x)\geqslant f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x)$
and(2)
 $f_{(S_{1}\#\cdots \#S_{n})_{p}}(x)=f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x)$
, for all
$f_{(S_{1}\#\cdots \#S_{n})_{p}}(x)=f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x)$
, for all
 $x\in \mathbb{R}$
, if and only if (mod
$x\in \mathbb{R}$
, if and only if (mod
 $p$
) reduction of the bundle
$p$
) reduction of the bundle
 $V_{1}\boxtimes \cdots \boxtimes V_{n}$
is strongly semistable on
$V_{1}\boxtimes \cdots \boxtimes V_{n}$
is strongly semistable on
 $(C_{1}\times \cdots \times C_{n})_{p}$
.
$(C_{1}\times \cdots \times C_{n})_{p}$
.
In particular,
(1)
 $e_{HK}^{\infty }(S_{1}\#\cdots \#S_{n})$
exists and
$e_{HK}^{\infty }(S_{1}\#\cdots \#S_{n})$
exists and
 $e_{HK}((S_{1}\#\cdots \#S_{n})_{p})\geqslant e_{HK}^{\infty }(S_{1}\#\cdots \#S_{n})$
, and
$e_{HK}((S_{1}\#\cdots \#S_{n})_{p})\geqslant e_{HK}^{\infty }(S_{1}\#\cdots \#S_{n})$
, and(2)
 $e_{HK}((S_{1}\#\cdots \#S_{n})_{p})=e_{HK}^{\infty }(S_{1}\#\cdots \#S_{n})$
if and only if (mod
$e_{HK}((S_{1}\#\cdots \#S_{n})_{p})=e_{HK}^{\infty }(S_{1}\#\cdots \#S_{n})$
if and only if (mod
 $p$
) reduction of the bundle
$p$
) reduction of the bundle
 $V_{1}\boxtimes \cdots \boxtimes V_{n}$
is strongly semistable on
$V_{1}\boxtimes \cdots \boxtimes V_{n}$
is strongly semistable on
 $(C_{1}\times \cdots \times C_{n})_{p}$
,
$(C_{1}\times \cdots \times C_{n})_{p}$
,
where the HK density functions and HK multiplicities are considered with respect to the ideal
![]() $\mathbf{m}_{1}\#\cdots \#\mathbf{m}_{n}$
for the graded maximal ideals
$\mathbf{m}_{1}\#\cdots \#\mathbf{m}_{n}$
for the graded maximal ideals
![]() $\mathbf{m}_{i}\subset S_{i}$
.
$\mathbf{m}_{i}\subset S_{i}$
.
Remark 4.8. With the notations and assumptions as in the corollary above, one can easily compute
![]() $f_{S_{1}\#\cdots \#S_{n}}^{\infty }$
, in terms of ranks of
$f_{S_{1}\#\cdots \#S_{n}}^{\infty }$
, in terms of ranks of
![]() $V_{i}$
and degrees of
$V_{i}$
and degrees of
![]() $C_{i}$
. In particular, if
$C_{i}$
. In particular, if
![]() $d_{1}=\deg C_{1}$
and
$d_{1}=\deg C_{1}$
and
![]() $d_{2}=\deg C_{2}$
, with
$d_{2}=\deg C_{2}$
, with
![]() $r=\text{rank}~V_{1}\geqslant s=\text{rank}~V_{2}$
, then it follows that
$r=\text{rank}~V_{1}\geqslant s=\text{rank}~V_{2}$
, then it follows that
Notations 4.9. Let
![]() $R=k[x,y,z]/(h)$
be a plane trinomial curve of degree
$R=k[x,y,z]/(h)$
be a plane trinomial curve of degree
![]() $d$
. That is,
$d$
. That is,
![]() $h=M_{1}+M_{2}+M_{3}$
, where the
$h=M_{1}+M_{2}+M_{3}$
, where the
![]() $M_{i}$
are monomials of degree
$M_{i}$
are monomials of degree
![]() $d$
. As given in [Reference MonskyMo2, Lemma 2.2], one can divide such an
$d$
. As given in [Reference MonskyMo2, Lemma 2.2], one can divide such an
![]() $h$
into two types.
$h$
into two types.
(1)
 $h$
is irregular; that is, one of the points
$h$
is irregular; that is, one of the points
 $(1,0,0)$
,
$(1,0,0)$
,
 $(0,1,0)$
,
$(0,1,0)$
,
 $(0,0,1)$
of
$(0,0,1)$
of
 $\mathbb{P}^{2}$
has multiplicity
$\mathbb{P}^{2}$
has multiplicity
 ${\geqslant}d/2$
on the plane curve
${\geqslant}d/2$
on the plane curve
 $h$
. Here, we define
$h$
. Here, we define
 $\unicode[STIX]{x1D706}_{R}=1$
.
$\unicode[STIX]{x1D706}_{R}=1$
.(2)
 $h$
is regular and hence is one of the following types (up to a change of variables).
$h$
is regular and hence is one of the following types (up to a change of variables).(a)
 $h=x^{a_{1}}y^{a_{2}}+y^{b_{1}}z^{b_{2}}+z^{c_{1}}x^{c_{2}}$
, where
$h=x^{a_{1}}y^{a_{2}}+y^{b_{1}}z^{b_{2}}+z^{c_{1}}x^{c_{2}}$
, where
 $a_{1},b_{1},c_{1}>d/2$
. Here, we define
$a_{1},b_{1},c_{1}>d/2$
. Here, we define
 $\unicode[STIX]{x1D6FC}=a_{1}+b_{1}-d$
,
$\unicode[STIX]{x1D6FC}=a_{1}+b_{1}-d$
,
 $\unicode[STIX]{x1D6FD}=a_{1}+c_{1}-d$
,
$\unicode[STIX]{x1D6FD}=a_{1}+c_{1}-d$
,
 $\unicode[STIX]{x1D708}=b_{1}+c_{1}-d$
, and
$\unicode[STIX]{x1D708}=b_{1}+c_{1}-d$
, and
 $\unicode[STIX]{x1D706}=a_{1}b_{1}+a_{2}c_{2}-b_{1}c_{2}$
.
$\unicode[STIX]{x1D706}=a_{1}b_{1}+a_{2}c_{2}-b_{1}c_{2}$
.(b)
 $h=x^{d}+x^{a_{1}}y^{a_{2}}z^{a_{3}}+y^{b}z^{c}$
, where
$h=x^{d}+x^{a_{1}}y^{a_{2}}z^{a_{3}}+y^{b}z^{c}$
, where
 $a_{2},c>d/2$
. Here, we define
$a_{2},c>d/2$
. Here, we define
 $\unicode[STIX]{x1D6FC}=a_{2}$
,
$\unicode[STIX]{x1D6FC}=a_{2}$
,
 $\unicode[STIX]{x1D6FD}=c$
,
$\unicode[STIX]{x1D6FD}=c$
,
 $\unicode[STIX]{x1D708}=a_{2}+c-d$
, and
$\unicode[STIX]{x1D708}=a_{2}+c-d$
, and
 $\unicode[STIX]{x1D706}=a_{2}c-a_{3}b$
.
$\unicode[STIX]{x1D706}=a_{2}c-a_{3}b$
.
We denote
 $\unicode[STIX]{x1D706}_{h}=\unicode[STIX]{x1D706}/a$
, where
$\unicode[STIX]{x1D706}_{h}=\unicode[STIX]{x1D706}/a$
, where
 $a=\text{g.c.d.}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D708},\unicode[STIX]{x1D706})$
.
$a=\text{g.c.d.}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D708},\unicode[STIX]{x1D706})$
.
Corollary 4.10. Let
![]() $S_{1},\ldots ,S_{n}$
be a set of irreducible plane trinomial curves given by trinomials
$S_{1},\ldots ,S_{n}$
be a set of irreducible plane trinomial curves given by trinomials
![]() $h_{1},\ldots ,h_{n}$
of degree
$h_{1},\ldots ,h_{n}$
of degree
![]() $d_{1},\ldots ,d_{n}\geqslant 4$
, respectively, over a field of characteristic
$d_{1},\ldots ,d_{n}\geqslant 4$
, respectively, over a field of characteristic
![]() $0$
. Then, there are spreads
$0$
. Then, there are spreads
![]() $\{(A_{i},S_{iA},\mathbf{m}_{iA})\}_{i}$
such that for every closed point
$\{(A_{i},S_{iA},\mathbf{m}_{iA})\}_{i}$
such that for every closed point
![]() $s\in \text{Spec}(A)$
,
$s\in \text{Spec}(A)$
,
(1)
 $f^{s}(S_{1}\#\cdots \#S_{n})(x)=f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x)$
, for all
$f^{s}(S_{1}\#\cdots \#S_{n})(x)=f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x)$
, for all
 $x\in \mathbb{R}$
, if
$x\in \mathbb{R}$
, if
 $\text{char}~k(s)\equiv \pm 1~(\text{mod}~\text{l.c.m.}(\unicode[STIX]{x1D706}_{h_{1}},\ldots ,\unicode[STIX]{x1D706}_{h_{n}}))$
, where
$\text{char}~k(s)\equiv \pm 1~(\text{mod}~\text{l.c.m.}(\unicode[STIX]{x1D706}_{h_{1}},\ldots ,\unicode[STIX]{x1D706}_{h_{n}}))$
, where
 $\unicode[STIX]{x1D706}_{h_{i}}$
is given as in Notations 4.9. In particular, there are infinitely many primes
$\unicode[STIX]{x1D706}_{h_{i}}$
is given as in Notations 4.9. In particular, there are infinitely many primes
 $p_{s}=\text{char}~k(s)$
such that the function
$p_{s}=\text{char}~k(s)$
such that the function
 $f_{(S_{1}\#\cdots \#S_{n})_{p_{s}}}-f_{S_{1}\#\cdots \#S_{n}}^{\infty }=0$
. Moreover,
$f_{(S_{1}\#\cdots \#S_{n})_{p_{s}}}-f_{S_{1}\#\cdots \#S_{n}}^{\infty }=0$
. Moreover,(2) if, in addition, one of the curves, say
 $S_{1}$
, is given by a symmetric trinomial
$S_{1}$
, is given by a symmetric trinomial
 $h_{1}=x^{a_{1}}y^{a_{2}}+y^{a_{1}}z^{a_{2}}+z^{a_{1}}x^{a_{2}}$
such that
$h_{1}=x^{a_{1}}y^{a_{2}}+y^{a_{1}}z^{a_{2}}+z^{a_{1}}x^{a_{2}}$
such that
 $d\neq 5$
, then for some
$d\neq 5$
, then for some $$\begin{eqnarray}f^{s}(S_{1}\#\cdots \#S_{n})(x_{0})>f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x_{0}),\quad \text{if}~\text{char}~k(s)\equiv \pm l\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D706}_{h_{1}}),\end{eqnarray}$$
$$\begin{eqnarray}f^{s}(S_{1}\#\cdots \#S_{n})(x_{0})>f_{S_{1}\#\cdots \#S_{n}}^{\infty }(x_{0}),\quad \text{if}~\text{char}~k(s)\equiv \pm l\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D706}_{h_{1}}),\end{eqnarray}$$
 $x_{0}\in \mathbb{R}$
and for some
$x_{0}\in \mathbb{R}$
and for some
 $l\in (\mathbb{Z}/\unicode[STIX]{x1D706}_{h_{1}}\mathbb{Z})^{\ast }$
. In particular, there are infinitely many primes
$l\in (\mathbb{Z}/\unicode[STIX]{x1D706}_{h_{1}}\mathbb{Z})^{\ast }$
. In particular, there are infinitely many primes
 $p_{s}=\text{char}~k(s)$
such that
$p_{s}=\text{char}~k(s)$
such that
 $f^{s}(S_{1}\#\cdots \#S_{n})-f_{S_{1}\#\cdots \#S_{n}}^{\infty }\neq 0$
.
$f^{s}(S_{1}\#\cdots \#S_{n})-f_{S_{1}\#\cdots \#S_{n}}^{\infty }\neq 0$
.
Proof. We can choose spreads
![]() $(A,S_{iA})$
with the property that
$(A,S_{iA})$
with the property that
![]() $\text{char}~k(s)>\max {\{d_{1},\ldots ,d_{n}\}}^{2}$
, for every closed point
$\text{char}~k(s)>\max {\{d_{1},\ldots ,d_{n}\}}^{2}$
, for every closed point
![]() $s\in \text{Spec}(A)$
. Now, for any irreducible plane curve given by
$s\in \text{Spec}(A)$
. Now, for any irreducible plane curve given by
![]() $S=k[x,y,z]/(h)$
, let
$S=k[x,y,z]/(h)$
, let
![]() $S\longrightarrow \tilde{S}$
be the normalization of
$S\longrightarrow \tilde{S}$
be the normalization of
![]() $S$
. Then, it is a finite graded map of degree 0 and
$S$
. Then, it is a finite graded map of degree 0 and
![]() $Q(S)=Q(\tilde{S})$
such that
$Q(S)=Q(\tilde{S})$
such that
![]() $\tilde{S}$
is a finitely generated
$\tilde{S}$
is a finitely generated
![]() $\mathbb{N}$
-graded two-dimensional domain over
$\mathbb{N}$
-graded two-dimensional domain over
![]() $k$
. Now, for pairs
$k$
. Now, for pairs
![]() $(S,\mathbf{m})$
and
$(S,\mathbf{m})$
and
![]() $(\tilde{S},\mathbf{m}\tilde{S})$
, we can choose a spread
$(\tilde{S},\mathbf{m}\tilde{S})$
, we can choose a spread
![]() $(A,S_{A},\mathbf{m}_{A})$
and
$(A,S_{A},\mathbf{m}_{A})$
and
![]() $(A,\tilde{S}_{A},\mathbf{m}\tilde{S}_{A})$
such that for every closed point
$(A,\tilde{S}_{A},\mathbf{m}\tilde{S}_{A})$
such that for every closed point
![]() $s\in \text{Spec}(A)$
, the natural map
$s\in \text{Spec}(A)$
, the natural map
![]() $S_{s}=S_{A}\otimes k(s)\longrightarrow \tilde{S}_{A}\otimes k(s)$
is a finite graded map of degree 0. This implies, for every
$S_{s}=S_{A}\otimes k(s)\longrightarrow \tilde{S}_{A}\otimes k(s)$
is a finite graded map of degree 0. This implies, for every
![]() $x\geqslant 0$
,
$x\geqslant 0$
,
 $$\begin{eqnarray}\lim _{q\rightarrow \infty }\frac{1}{q}\ell \left(\frac{S_{s}}{\mathbf{m}^{[q]}}\right)_{\lfloor xq\rfloor }=\lim _{q\rightarrow \infty }\frac{1}{q}\ell \left(\frac{\tilde{S}_{s}}{\mathbf{m}{\tilde{S}_{s}}^{[q]}}\right)_{\lfloor xq\rfloor },\end{eqnarray}$$
$$\begin{eqnarray}\lim _{q\rightarrow \infty }\frac{1}{q}\ell \left(\frac{S_{s}}{\mathbf{m}^{[q]}}\right)_{\lfloor xq\rfloor }=\lim _{q\rightarrow \infty }\frac{1}{q}\ell \left(\frac{\tilde{S}_{s}}{\mathbf{m}{\tilde{S}_{s}}^{[q]}}\right)_{\lfloor xq\rfloor },\end{eqnarray}$$
as kernel and cokernel of the map
![]() $S_{s}\longrightarrow \tilde{S}_{s}$
are zero-dimensional. Therefore,
$S_{s}\longrightarrow \tilde{S}_{s}$
are zero-dimensional. Therefore,
![]() $f_{S_{s},\mathbf{m}_{s}}=f_{\tilde{S}_{s},\mathbf{m}\tilde{S}_{s}}$
and
$f_{S_{s},\mathbf{m}_{s}}=f_{\tilde{S}_{s},\mathbf{m}\tilde{S}_{s}}$
and
![]() $f_{S,\mathbf{m}}^{\infty }=f_{\tilde{S},\mathbf{m}\tilde{S}}^{\infty }$
. This also implies that
$f_{S,\mathbf{m}}^{\infty }=f_{\tilde{S},\mathbf{m}\tilde{S}}^{\infty }$
. This also implies that
![]() $e_{HK}(S_{s},\mathbf{m}_{s})=e_{HK}(\tilde{S}_{s},\mathbf{m}\tilde{S}_{s})$
. (This inequality about
$e_{HK}(S_{s},\mathbf{m}_{s})=e_{HK}(\tilde{S}_{s},\mathbf{m}\tilde{S}_{s})$
. (This inequality about
![]() $e_{HK}$
can also be found in [Reference MonskyMo1, Lemma 1.3], [Reference Watanabe and YoshidaWY1, Theorem 2.7], and [Reference Buchweitz, Chen and PardueBCP].) Let
$e_{HK}$
can also be found in [Reference MonskyMo1, Lemma 1.3], [Reference Watanabe and YoshidaWY1, Theorem 2.7], and [Reference Buchweitz, Chen and PardueBCP].) Let
![]() $\unicode[STIX]{x1D70B}:\tilde{X}_{s}=\text{Proj}~\tilde{S}_{s}\longrightarrow X_{s}=\text{Proj}~S_{s}$
be the induced map. We also choose a spread
$\unicode[STIX]{x1D70B}:\tilde{X}_{s}=\text{Proj}~\tilde{S}_{s}\longrightarrow X_{s}=\text{Proj}~S_{s}$
be the induced map. We also choose a spread
![]() $(A,X_{A},V_{A})$
, where
$(A,X_{A},V_{A})$
, where
![]() $V_{A}$
is given by
$V_{A}$
is given by
and gives the syzygy bundle
![]() $V_{s}$
with its HN filtration as given in Example 4.5.
$V_{s}$
with its HN filtration as given in Example 4.5.
This gives a short exact sequence of sheaves of
![]() ${\mathcal{O}}_{\tilde{X}_{s}}$
-modules
${\mathcal{O}}_{\tilde{X}_{s}}$
-modules
Moreover,
![]() $\tilde{X}_{s}$
is a nonsingular curve. If
$\tilde{X}_{s}$
is a nonsingular curve. If
![]() $S$
is regular trinomial given by
$S$
is regular trinomial given by
![]() $h$
, then, by [Reference TrivediT5, Theorem 5.6], the bundle
$h$
, then, by [Reference TrivediT5, Theorem 5.6], the bundle
![]() $\unicode[STIX]{x1D70B}^{\ast }(V_{s})$
is strongly semistable, provided that
$\unicode[STIX]{x1D70B}^{\ast }(V_{s})$
is strongly semistable, provided that
![]() $\text{char}~k(s)\equiv \pm 1~(\text{mod}~2\unicode[STIX]{x1D706}_{h_{s}})$
. Therefore, by Theorem 4.6, we have
$\text{char}~k(s)\equiv \pm 1~(\text{mod}~2\unicode[STIX]{x1D706}_{h_{s}})$
. Therefore, by Theorem 4.6, we have
![]() $f_{\tilde{S}_{s},\mathbf{m}\tilde{S}_{s}}=f_{\tilde{S},\mathbf{m}\tilde{S}}^{\infty }$
. This implies that
$f_{\tilde{S}_{s},\mathbf{m}\tilde{S}_{s}}=f_{\tilde{S},\mathbf{m}\tilde{S}}^{\infty }$
. This implies that
![]() $f_{S_{s},\mathbf{m}_{s}}=f_{S,\mathbf{m}}^{\infty }$
, for
$f_{S_{s},\mathbf{m}_{s}}=f_{S,\mathbf{m}}^{\infty }$
, for
![]() $\text{char}~k(s)\equiv \pm 1~(\text{mod}~2\unicode[STIX]{x1D706}_{S_{s}})$
.
$\text{char}~k(s)\equiv \pm 1~(\text{mod}~2\unicode[STIX]{x1D706}_{S_{s}})$
.
If
![]() $S$
is an irregular trinomial, then, by [Reference TrivediT5, Theorem 1.1],
$S$
is an irregular trinomial, then, by [Reference TrivediT5, Theorem 1.1],
![]() $\unicode[STIX]{x1D70B}^{\ast }V$
has an HN filtration
$\unicode[STIX]{x1D70B}^{\ast }V$
has an HN filtration
![]() $0\subset {\mathcal{L}}\subset \unicode[STIX]{x1D70B}^{\ast }V$
. Therefore,
$0\subset {\mathcal{L}}\subset \unicode[STIX]{x1D70B}^{\ast }V$
. Therefore,
![]() $0\subset {\mathcal{L}}_{s}\subset \unicode[STIX]{x1D70B}^{\ast }V_{s}$
is the HN filtration and hence the strong HN filtration (as
$0\subset {\mathcal{L}}_{s}\subset \unicode[STIX]{x1D70B}^{\ast }V_{s}$
is the HN filtration and hence the strong HN filtration (as
![]() $\text{rank}~V=2$
), for
$\text{rank}~V=2$
), for
![]() $\unicode[STIX]{x1D70B}^{\ast }V_{s}$
, for every closed point
$\unicode[STIX]{x1D70B}^{\ast }V_{s}$
, for every closed point
![]() $s\in \text{Spec}~A$
. In particular, by Theorem 4.6,
$s\in \text{Spec}~A$
. In particular, by Theorem 4.6,
![]() $f_{S_{s},\mathbf{m}_{s}}=f_{S,\mathbf{m}}^{\infty }$
, for all such
$f_{S_{s},\mathbf{m}_{s}}=f_{S,\mathbf{m}}^{\infty }$
, for all such
![]() $s$
. Now, assertion (1) follows by Proposition 4.4(2).
$s$
. Now, assertion (1) follows by Proposition 4.4(2).
If
![]() $S_{1}=k[x,y,z]/(h_{1})$
, where
$S_{1}=k[x,y,z]/(h_{1})$
, where
![]() $h_{1}$
is as in statement (2) of the corollary, then
$h_{1}$
is as in statement (2) of the corollary, then
![]() $\unicode[STIX]{x1D70B}^{\ast }V_{s}$
is semistable, but not strongly semistable, if
$\unicode[STIX]{x1D70B}^{\ast }V_{s}$
is semistable, but not strongly semistable, if
![]() $\text{char}~k(s)\equiv \pm 2~(\text{mod}~\unicode[STIX]{x1D706}_{{h_{1}}_{s}})$
. In particular, by Corollary 4.7,
$\text{char}~k(s)\equiv \pm 2~(\text{mod}~\unicode[STIX]{x1D706}_{{h_{1}}_{s}})$
. In particular, by Corollary 4.7,
![]() $f_{{S_{1}}_{s},\mathbf{m}{S_{1}}_{s}}>f_{{S_{1}}_{s},\mathbf{m}{S_{1}}_{s}}^{\infty }$
, for such
$f_{{S_{1}}_{s},\mathbf{m}{S_{1}}_{s}}>f_{{S_{1}}_{s},\mathbf{m}{S_{1}}_{s}}^{\infty }$
, for such
![]() $s$
. Therefore, the statement (2) follows from Proposition 4.4(2).◻
$s$
. Therefore, the statement (2) follows from Proposition 4.4(2).◻
Appendix A
Lemma A.1. For an integer
![]() $d\geqslant 2$
, there exist universal polynomials
$d\geqslant 2$
, there exist universal polynomials
![]() $P_{i}^{d}$
,
$P_{i}^{d}$
,
![]() $P_{i}^{\prime d}$
in
$P_{i}^{\prime d}$
in
![]() $\mathbb{Q}[X_{0},\ldots ,X_{i}]$
, where
$\mathbb{Q}[X_{0},\ldots ,X_{i}]$
, where
![]() $0\leqslant i\leqslant d-2$
, such that if, for a pair
$0\leqslant i\leqslant d-2$
, such that if, for a pair
![]() $(X,{\mathcal{O}}_{X}(1))$
, we have
$(X,{\mathcal{O}}_{X}(1))$
, we have
![]() $X$
an integral projective variety of char
$X$
an integral projective variety of char
![]() $p>0$
and dimension
$p>0$
and dimension
![]() $d-1$
, and
$d-1$
, and
![]() ${\mathcal{Q}}$
a coherent sheaf of
${\mathcal{Q}}$
a coherent sheaf of
![]() ${\mathcal{O}}_{X}$
-modules of
${\mathcal{O}}_{X}$
-modules of
![]() $\dim (\text{Supp}){\mathcal{Q}}=d-2$
and with the following respective Hilbert polynomials (where
$\dim (\text{Supp}){\mathcal{Q}}=d-2$
and with the following respective Hilbert polynomials (where
![]() $\dim \text{supp}{\mathcal{Q}}\leqslant d-2$
):
$\dim \text{supp}{\mathcal{Q}}\leqslant d-2$
):
and
then we have the following.
(1) For
 $0\leqslant i\leqslant d-2$
, we have
$0\leqslant i\leqslant d-2$
, we have
 $|q_{i}|\leqslant p^{d-1}P_{i}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{i+1}),$
if there is a short exact sequence of
$|q_{i}|\leqslant p^{d-1}P_{i}^{d}(\tilde{e}_{0},\ldots ,\tilde{e}_{i+1}),$
if there is a short exact sequence of
 ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules  $$\begin{eqnarray}0\longrightarrow \oplus ^{p^{d-1}}{\mathcal{O}}_{X}(-d)\longrightarrow F_{\ast }{\mathcal{O}}_{X}\longrightarrow {\mathcal{Q}}\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow \oplus ^{p^{d-1}}{\mathcal{O}}_{X}(-d)\longrightarrow F_{\ast }{\mathcal{O}}_{X}\longrightarrow {\mathcal{Q}}\longrightarrow 0.\end{eqnarray}$$
(2) For
 $0\leqslant i\leqslant d-2$
, we have
$0\leqslant i\leqslant d-2$
, we have
 $|q_{i}|\leqslant m_{0}^{i+1}P_{i}^{^{\prime }d}(\tilde{e}_{0},\ldots ,\tilde{e}_{i}),$
if
$|q_{i}|\leqslant m_{0}^{i+1}P_{i}^{^{\prime }d}(\tilde{e}_{0},\ldots ,\tilde{e}_{i}),$
if
 ${\mathcal{Q}}$
fits in the short exact sequence or in the short exact sequence
${\mathcal{Q}}$
fits in the short exact sequence or in the short exact sequence $$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{X}(-m_{0})\longrightarrow {\mathcal{O}}_{X}\longrightarrow {\mathcal{Q}}\longrightarrow 0\end{eqnarray}$$
of
$$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{X}(-m_{0})\longrightarrow {\mathcal{O}}_{X}\longrightarrow {\mathcal{Q}}\longrightarrow 0\end{eqnarray}$$
of $$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{X}\longrightarrow {\mathcal{O}}_{X}(m_{0})\longrightarrow {\mathcal{Q}}\longrightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{X}\longrightarrow {\mathcal{O}}_{X}(m_{0})\longrightarrow {\mathcal{Q}}\longrightarrow 0\end{eqnarray}$$
 ${\mathcal{O}}_{X}$
-modules.
${\mathcal{O}}_{X}$
-modules.
Proof. Assertion (1): Note that for
![]() $m\in \mathbb{Z}$
, we have
$m\in \mathbb{Z}$
, we have
We can express, for
![]() $1\leqslant n\leqslant d-1$
,
$1\leqslant n\leqslant d-1$
,
where
![]() $C_{n}^{n}=1$
, and, for
$C_{n}^{n}=1$
, and, for
![]() $j<n$
, the coefficient
$j<n$
, the coefficient
![]() $C_{j}^{n}$
is in the set
$C_{j}^{n}$
is in the set
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\sum \,x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}\left|\,\sum \,i_{l}=n-j,\right.0\leqslant j<n\leqslant d-1,\{x_{1},\ldots ,x_{n}\}\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.=\{1,\ldots ,n\}\vphantom{\sum }\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\sum \,x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}\left|\,\sum \,i_{l}=n-j,\right.0\leqslant j<n\leqslant d-1,\{x_{1},\ldots ,x_{n}\}\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.=\{1,\ldots ,n\}\vphantom{\sum }\right\}.\nonumber\end{eqnarray}$$
Now, expanding Equation (A.1), we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\tilde{e}_{0}}{(d-1)!} [C_{d-2}^{d-1}m^{d-2}(p^{d-2}-p^{d-1})+C_{d-3}^{d-1}m^{d-3}(p^{d-3}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +C_{0}^{d-1}(1-p^{d-1})]\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +\frac{(-1)^{i}\tilde{e}_{i}}{(d-1-i)!} [C_{d-1-i}^{d-1-i}m^{d-1-i}(p^{d-1-i}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C_{d-2-i}^{d-1-i}m^{d-2-i}(p^{d-2-i}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +C_{0}^{d-1-i}(1-p^{d-1})]+\cdots +(-1)^{d-1}\tilde{e}_{d-1}[(1-p^{d-1})]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{q_{0}}{(d-2)!}[C_{d-2}^{d-2}m^{d-2}+C_{d-3}^{d-2}m^{d-3}+\cdots +C_{0}^{d-2}]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{q_{1}}{(d-3)!}[C_{d-3}^{d-3}m^{d-3}+C_{d-4}^{d-3}m^{d-4}+\cdots +C_{0}^{d-3}]+\cdots \nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{i-1}q_{i-1}}{(d-1-i)!}[C_{d-1-i}^{d-1-i}m^{d-1-i}+C_{d-2-i}^{d-1-i}m^{d-2-i}+\cdots +C_{0}^{d-1-i}]\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +(-1)^{d-2}q_{d-2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\tilde{e}_{0}}{(d-1)!} [C_{d-2}^{d-1}m^{d-2}(p^{d-2}-p^{d-1})+C_{d-3}^{d-1}m^{d-3}(p^{d-3}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +C_{0}^{d-1}(1-p^{d-1})]\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +\frac{(-1)^{i}\tilde{e}_{i}}{(d-1-i)!} [C_{d-1-i}^{d-1-i}m^{d-1-i}(p^{d-1-i}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C_{d-2-i}^{d-1-i}m^{d-2-i}(p^{d-2-i}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +C_{0}^{d-1-i}(1-p^{d-1})]+\cdots +(-1)^{d-1}\tilde{e}_{d-1}[(1-p^{d-1})]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{q_{0}}{(d-2)!}[C_{d-2}^{d-2}m^{d-2}+C_{d-3}^{d-2}m^{d-3}+\cdots +C_{0}^{d-2}]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{q_{1}}{(d-3)!}[C_{d-3}^{d-3}m^{d-3}+C_{d-4}^{d-3}m^{d-4}+\cdots +C_{0}^{d-3}]+\cdots \nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(-1)^{i-1}q_{i-1}}{(d-1-i)!}[C_{d-1-i}^{d-1-i}m^{d-1-i}+C_{d-2-i}^{d-1-i}m^{d-2-i}+\cdots +C_{0}^{d-1-i}]\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots +(-1)^{d-2}q_{d-2}.\nonumber\end{eqnarray}$$
We prove the result for
![]() $q_{i}$
, by induction on
$q_{i}$
, by induction on
![]() $i$
. For
$i$
. For
![]() $i=0$
, comparing the coefficients of
$i=0$
, comparing the coefficients of
![]() $m^{d-2}$
on both sides, we get
$m^{d-2}$
on both sides, we get
which implies
Comparing coefficients of
![]() $m^{d-i}$
, we get
$m^{d-i}$
, we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle (p^{d-i}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left[\frac{\tilde{e}_{0}}{(d-1)!}C_{d-i}^{d-1}-\frac{\tilde{e}_{1}}{(d-2)!}C_{d-i}^{d-2}+\cdots +(-1)^{i-1}\frac{\tilde{e}_{i-1}}{(d-i)!}C_{d-i}^{d-1-i}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{q_{0}}{(d-2)!}C_{d-i}^{d-2}-\frac{q_{1}}{(d-3)!}C_{d-i}^{d-3}+\cdots +(-1)^{i}\frac{q_{i-2}}{(d-i)!}C_{d-i}^{d-i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (p^{d-i}-p^{d-1})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left[\frac{\tilde{e}_{0}}{(d-1)!}C_{d-i}^{d-1}-\frac{\tilde{e}_{1}}{(d-2)!}C_{d-i}^{d-2}+\cdots +(-1)^{i-1}\frac{\tilde{e}_{i-1}}{(d-i)!}C_{d-i}^{d-1-i}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{q_{0}}{(d-2)!}C_{d-i}^{d-2}-\frac{q_{1}}{(d-3)!}C_{d-i}^{d-3}+\cdots +(-1)^{i}\frac{q_{i-2}}{(d-i)!}C_{d-i}^{d-i}.\nonumber\end{eqnarray}$$
This implies that
However,
Now, the proof follows by induction.
Assertion (2): For
![]() $m_{0}=0$
, the statement is true vacuously. Therefore, we can assume that
$m_{0}=0$
, the statement is true vacuously. Therefore, we can assume that
![]() $m_{0}\geqslant 1$
. Now,
$m_{0}\geqslant 1$
. Now,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(X,{\mathcal{Q}}(m)) & = & \displaystyle q_{0}\binom{m+d-2}{d-2}-q_{1}\binom{m+d-3}{d-3}+\cdots +(-1)^{d-2}q_{d-2},\nonumber\\ \displaystyle & = & \displaystyle \frac{q_{0}}{(d-2)!}[D_{d-2}^{d-2}m^{d-2}+D_{d-3}^{d-2}m^{d-3}+\cdots +D_{0}^{d-2}]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{q_{1}}{(d-3)!}[D_{d-3}^{d-3}m^{d-3}+D_{d-4}^{d-3}m^{d-4}+\cdots +D_{0}^{d-3}]\nonumber\\ \displaystyle & & \displaystyle +\cdots +\frac{(-1)^{i-1}q_{i-1}}{(d-1-i)!} [D_{d-1-i}^{d-1-i}m^{d-1-i}+D_{d-2-i}^{d-1-i}m^{d-2-i}\nonumber\\ \displaystyle & & \displaystyle +\cdots +D_{0}^{d-1-i} ]+\cdots +(-1)^{d-2}q_{d-2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(X,{\mathcal{Q}}(m)) & = & \displaystyle q_{0}\binom{m+d-2}{d-2}-q_{1}\binom{m+d-3}{d-3}+\cdots +(-1)^{d-2}q_{d-2},\nonumber\\ \displaystyle & = & \displaystyle \frac{q_{0}}{(d-2)!}[D_{d-2}^{d-2}m^{d-2}+D_{d-3}^{d-2}m^{d-3}+\cdots +D_{0}^{d-2}]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{q_{1}}{(d-3)!}[D_{d-3}^{d-3}m^{d-3}+D_{d-4}^{d-3}m^{d-4}+\cdots +D_{0}^{d-3}]\nonumber\\ \displaystyle & & \displaystyle +\cdots +\frac{(-1)^{i-1}q_{i-1}}{(d-1-i)!} [D_{d-1-i}^{d-1-i}m^{d-1-i}+D_{d-2-i}^{d-1-i}m^{d-2-i}\nonumber\\ \displaystyle & & \displaystyle +\cdots +D_{0}^{d-1-i} ]+\cdots +(-1)^{d-2}q_{d-2},\nonumber\end{eqnarray}$$
where
![]() $D_{j}^{k}$
belongs to the set
$D_{j}^{k}$
belongs to the set
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\sum \,x^{i_{1}}\cdots x_{k}^{i_{k}}\left|\,\sum \,i_{l}=k-j\quad 0\leqslant j\leqslant k\leqslant d-2,\right.\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\{x_{1},\ldots ,x_{k}\}=\{1,\ldots ,k\}\vphantom{\sum }\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\sum \,x^{i_{1}}\cdots x_{k}^{i_{k}}\left|\,\sum \,i_{l}=k-j\quad 0\leqslant j\leqslant k\leqslant d-2,\right.\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\{x_{1},\ldots ,x_{k}\}=\{1,\ldots ,k\}\vphantom{\sum }\right\}.\nonumber\end{eqnarray}$$
On the other hand,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m))-\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m-m_{0}))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\tilde{e}_{0}}{(d-1)!} [C_{d-1}^{d-1}(m_{0})(m^{d-2}+\cdots m^{d-3}m_{0}+\cdots +m_{0}^{d-2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C_{d-2}^{d-1}(m_{0})(m^{d-3}+m^{d-4}m_{0}+\cdots +m_{0}^{d-3})+\cdots +C_{1}^{d-1}(m_{0})]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\tilde{e}_{1}}{(d-2)!} [C_{d-2}^{d-2}(m_{0})(m^{d-3}+\cdots m^{d-4}m_{0}+\cdots +m_{0}^{d-3})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C_{d-3}^{d-2}(m_{0})(m^{d-4}+m^{d-5}m_{0}+\cdots +m_{0}^{d-4})+\cdots +C_{1}^{d-2}(m_{0})]\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots \,.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m))-\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m-m_{0}))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\tilde{e}_{0}}{(d-1)!} [C_{d-1}^{d-1}(m_{0})(m^{d-2}+\cdots m^{d-3}m_{0}+\cdots +m_{0}^{d-2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C_{d-2}^{d-1}(m_{0})(m^{d-3}+m^{d-4}m_{0}+\cdots +m_{0}^{d-3})+\cdots +C_{1}^{d-1}(m_{0})]\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\tilde{e}_{1}}{(d-2)!} [C_{d-2}^{d-2}(m_{0})(m^{d-3}+\cdots m^{d-4}m_{0}+\cdots +m_{0}^{d-3})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,C_{d-3}^{d-2}(m_{0})(m^{d-4}+m^{d-5}m_{0}+\cdots +m_{0}^{d-4})+\cdots +C_{1}^{d-2}(m_{0})]\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots \,.\nonumber\end{eqnarray}$$
Again, we prove the result for
![]() $q_{i}$
, by induction on
$q_{i}$
, by induction on
![]() $i$
. Comparing the coefficients for
$i$
. Comparing the coefficients for
![]() $m^{d-2}$
, we get
$m^{d-2}$
, we get
Comparing the coefficients of
![]() $m^{d-i}$
, where
$m^{d-i}$
, where
![]() $2\leqslant i\leqslant d$
, we get
$2\leqslant i\leqslant d$
, we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{q_{0}}{(d-2)!}D_{d-i}^{d-2}-\frac{q_{1}}{(d-3)!}D_{d-i}^{d-3}+\cdots +(-1)^{i-2}\frac{q_{i-2}}{(d-i)!}D_{d-i}^{d-i}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\tilde{e}_{0}}{(d-1)!}(C_{d-1}^{d-1}m_{0}^{i-1}+C_{d-2}^{d-1}m_{0}^{i-2}+\cdots +C_{d-i+1}^{d-1}m_{0})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\tilde{e}_{1}}{(d-2)!}(C_{d-2}^{d-2}m_{0}^{i-2}+C_{d-3}^{d-2}m_{0}^{i-3}+\cdots +C_{d-i+1}^{d-2}m_{0})\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots (-1)^{i-2}\frac{\tilde{e}_{i-2}}{(d+1-i)!}(C_{d+1-i}^{d-i+1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{q_{0}}{(d-2)!}D_{d-i}^{d-2}-\frac{q_{1}}{(d-3)!}D_{d-i}^{d-3}+\cdots +(-1)^{i-2}\frac{q_{i-2}}{(d-i)!}D_{d-i}^{d-i}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\tilde{e}_{0}}{(d-1)!}(C_{d-1}^{d-1}m_{0}^{i-1}+C_{d-2}^{d-1}m_{0}^{i-2}+\cdots +C_{d-i+1}^{d-1}m_{0})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{\tilde{e}_{1}}{(d-2)!}(C_{d-2}^{d-2}m_{0}^{i-2}+C_{d-3}^{d-2}m_{0}^{i-3}+\cdots +C_{d-i+1}^{d-2}m_{0})\nonumber\\ \displaystyle & & \displaystyle \qquad +\cdots (-1)^{i-2}\frac{\tilde{e}_{i-2}}{(d+1-i)!}(C_{d+1-i}^{d-i+1}).\nonumber\end{eqnarray}$$
This implies that
 $$\begin{eqnarray}\displaystyle |q_{i-2}||D_{d-i}^{d-i}| & {\leqslant} & \displaystyle |\tilde{e}_{0}|(C_{d-1}^{d-1}m_{0}^{i-1}+\cdots +C_{d-i+1}^{d-1}m_{0})\nonumber\\ \displaystyle & & \displaystyle +\,|\tilde{e}_{1}|(C_{d-2}^{d-2}m_{0}^{i-2}+\cdots +C_{d-i+1}^{d-2}m_{0})\nonumber\\ \displaystyle & & \displaystyle +\cdots +|\tilde{e}_{i-2}|(C_{d+1-i}^{d+1-i})\nonumber\\ \displaystyle & & \displaystyle +\,(|q_{0}||D_{d-i}^{d-2}|+|q_{1}||D_{d-i}^{d-3}|+\cdots +|q_{i-3}||D_{d-i}^{d+1-i}|).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |q_{i-2}||D_{d-i}^{d-i}| & {\leqslant} & \displaystyle |\tilde{e}_{0}|(C_{d-1}^{d-1}m_{0}^{i-1}+\cdots +C_{d-i+1}^{d-1}m_{0})\nonumber\\ \displaystyle & & \displaystyle +\,|\tilde{e}_{1}|(C_{d-2}^{d-2}m_{0}^{i-2}+\cdots +C_{d-i+1}^{d-2}m_{0})\nonumber\\ \displaystyle & & \displaystyle +\cdots +|\tilde{e}_{i-2}|(C_{d+1-i}^{d+1-i})\nonumber\\ \displaystyle & & \displaystyle +\,(|q_{0}||D_{d-i}^{d-2}|+|q_{1}||D_{d-i}^{d-3}|+\cdots +|q_{i-3}||D_{d-i}^{d+1-i}|).\nonumber\end{eqnarray}$$
Now, the proof follows by induction.
For
![]() ${\mathcal{Q}}$
such that
${\mathcal{Q}}$
such that
![]() $0\longrightarrow {\mathcal{O}}_{X}\longrightarrow {\mathcal{O}}_{X}(m_{0})\longrightarrow {\mathcal{Q}}\longrightarrow 0,$
we have
$0\longrightarrow {\mathcal{O}}_{X}\longrightarrow {\mathcal{O}}_{X}(m_{0})\longrightarrow {\mathcal{Q}}\longrightarrow 0,$
we have
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{Q}}(m-m_{0}))=\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m))-\unicode[STIX]{x1D712}(X,{\mathcal{O}}(m-m_{0}))$
, so we get the same bounds for the
$\unicode[STIX]{x1D712}(X,{\mathcal{Q}}(m-m_{0}))=\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}(m))-\unicode[STIX]{x1D712}(X,{\mathcal{O}}(m-m_{0}))$
, so we get the same bounds for the
![]() $q_{i}$
in terms of the
$q_{i}$
in terms of the
![]() $\tilde{e}_{j}$
as above except that now
$\tilde{e}_{j}$
as above except that now
![]() $D_{j}^{n}$
is in the set
$D_{j}^{n}$
is in the set
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\sum \,x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}\left|\,\mathop{\sum }_{l=1}^{n}i_{l}=n-j,0\leqslant j\leqslant n,\right.\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\{x_{1},\ldots ,x_{n}\}=\{1-m_{0},\ldots ,n-m_{0}\}\vphantom{\mathop{\sum }_{i=1}^{n}}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left\{\sum \,x_{1}^{i_{1}}\cdots x_{n}^{i_{n}}\left|\,\mathop{\sum }_{l=1}^{n}i_{l}=n-j,0\leqslant j\leqslant n,\right.\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\{x_{1},\ldots ,x_{n}\}=\{1-m_{0},\ldots ,n-m_{0}\}\vphantom{\mathop{\sum }_{i=1}^{n}}\right\}.\nonumber\end{eqnarray}$$
Hence, the lemma follows. ◻