Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T21:46:54.030Z Has data issue: false hasContentIssue false
  • English
  • Français

The topology of an open manifold with radial curvature bounded from below by a model surface with finite total curvature and examples of model surfaces

Published online by Cambridge University Press:  11 January 2016

Minoru Tanaka  and
Kei Kondo
Minoru Tanaka
Affiliation:
Department of Mathematics, Tokai University, Hiratsuka City, Kanagawa Pref. 259 – 1292, Japan, [email protected]
Kei Kondo
Affiliation:
Department of Mathematics, Tokai University, Hiratsuka City, Kanagawa Pref. 259 – 1292, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct distinctive surfaces of revolution with finite total curvature whose Gauss curvatures are not bounded. Such a surface of revolution is employed as a reference surface of comparison theorems in radial curvature geometry. Moreover, we prove that a complete noncompact Riemannian manifold M is homeomorphic to the interior of a compact manifold with boundary if the manifold M is not less curved than a noncompact model surface 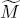of revolution and if the total curvature of the model surface 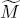is finite and less than 2π. By the first result mentioned above, the second result covers a much wider class of manifolds than that of complete noncompact Riemannian manifolds whose sectional curvatures are bounded from below by a constant.

Keywords

53C2153C22
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 209 , March 2013 , pp. 23 - 34
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2013

References

[CV] Cohn-Vossen, S., Totalkrümmung und geodätische Linien auf einfachzusammenhängenden offenen vollständigen Flächenstücken, Rec. Math. Moscou (2) 1 (1936), 139–163. Zbl 0014.27601.Google Scholar
[KT1] Kondo, K. and Tanaka, M., Total curvatures of model surfaces control topology of complete open manifolds with radial curvature bounded below, II, Trans. Amer. Math. Soc. 362 (2010), 6293–6324. MR 2678975. DOI 10.1090/S0002-9947-2010-05031-7.CrossRefGoogle Scholar
[KT2] Kondo, K. and Tanaka, M., Total curvatures of model surfaces control topology of complete open manifolds with radial curvature bounded below, I, Math. Ann. 351 (2011), 251–266. MR 2836657. DOI 10.1007/s00208-010-0593-4.Google Scholar
[KT3] Kondo, K. and Tanaka, M., Total curvatures of model surfaces control topology of complete open manifolds with radial curvature bounded below, III, J. Math. Soc. Japan 64 (2012), 185–200. MR 2879741. DOI 10.2969/jmsj/06410185.CrossRefGoogle Scholar
[SST] Shiohama, K., Shioya, T., and Tanaka, M., The Geometry of Total Curvature on Complete Open Surfaces, Cambridge Tracts in Math. 159, Cambridge University Press, Cambridge, 2003. MR 2028047. DOI 10.1017/CBO9780511543159.Google Scholar