Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T04:50:38.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Tangent loci and certain linear sections of adjoint varieties

Published online by Cambridge University Press:  22 January 2016

Hajime Kaji  and
Osami Yasukura
Hajime Kaji
Affiliation:
Department of Mathematical Sciences, School of Science and Engineering, Waseda University, Tokyo, 169-8555, Japan, [email protected]
Osami Yasukura
Affiliation:
Department of Mathematics, Fukui University, Fukui 910-8507, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An adjoint variety X(g)associated to a complex simple Lie algebra is by definition a projective variety in ℙ*(g) obtained as the projectivization of the (unique) non-zero, minimal nilpotent orbit in g. We first describe the tangent loci of X(g) in terms of 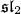triples. Secondly for a graded decomposition of contact type 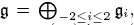we show that the intersection of X(g) and the linear subspace ℙ*(g1) in ℙ*(g) coincides with the cubic Veronese variety associated to g.

Keywords

14M1717B7017B2014N05
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 158 , December 2000 , pp. 63 - 72
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2000

References

[A1] Asano, H., On triple systems (in Japanese), Yokohama City Univ. Ronso, Ser. Natural Sci., 27 (1975), 7–31.Google Scholar
[A2] Asano, H., Symplectic triple systems and simple Lie algebras (in Japanese), RIMS Kokyuroku, Kyoto Univ., 308 (1977), 41–54.Google Scholar
[CM] Collingwood, D. H. and McGovern, W. M., Nilpotent orbits in semisimple Liealgebras, Van Nostrand Reinhold, New York, 1993.Google Scholar
[F] Freudenthal, H., Lie groups in the foundations of geometry, Advances in Math., 1 (1964), 145–190.Google Scholar
[FR] Fujita, T. and Roberts, J., Varieties with small secant varieties: The extremal case, Amer. J. Math., 103 (1981), 953–976.Google Scholar
[FH] Fulton, W. and Harris, J., Representation Theory: A First Course, GTM 129, Springer-Verlag, New York, 1991.Google Scholar
[H1] Humphreys, J. E., Introduction to Lie algebras and representation theory, GTM 9, Springer-Verlag, New York, 1972.Google Scholar
[H2] Humphreys, J. E., Linear Algebraic Groups, GTM 21, Springer-Verlag, New York, 1975.Google Scholar
[KOY] Kaji, H., Ohno, M. and Yasukura, O., Adjoint varieties and their secant varieties, Indag. Math., 10 (1999), 45–57.Google Scholar
[M] Mukai, S., Projective geometry of homogeneous spaces (in Japanese), Proc. Symp. Algebraic Geometry, “Projective Varieties/Projective Geometry of Algebraic Varieties”, Waseda University, Japan (1994), pp. 1–52.Google Scholar